↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Generating realistic-looking hair remains a challenge in computer graphics. Existing methods often struggle with capturing fine details and creating hairstyles with nuanced high-frequency features, such as curls and flyaways. Current techniques often simplify the process by using low-resolution guide hairs, which leads to a loss of detail and sometimes unnatural results.
This paper presents a novel approach that leverages a doubly hierarchical representation of hair geometry to address this problem. The approach involves separating low-frequency structural curves from high-frequency details, utilizing the Discrete Cosine Transform to mitigate Gibbs oscillations, and employing k-medoids clustering for optimal guide strand sampling. The resulting model is able to generate convincing and high-quality guide hair and dense hair strands, even with complex morphologies. This method is efficient and flexible, creating superior results compared to previous approaches.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel approach to realistic hair generation in computer graphics, addressing the limitations of existing methods. Its doubly hierarchical generative model offers enhanced flexibility and efficiency, enabling the creation of convincing hairstyles with high-frequency details. This advances the state-of-the-art and opens new avenues for research in virtual human generation, virtual reality, and related fields.
Visual Insights#

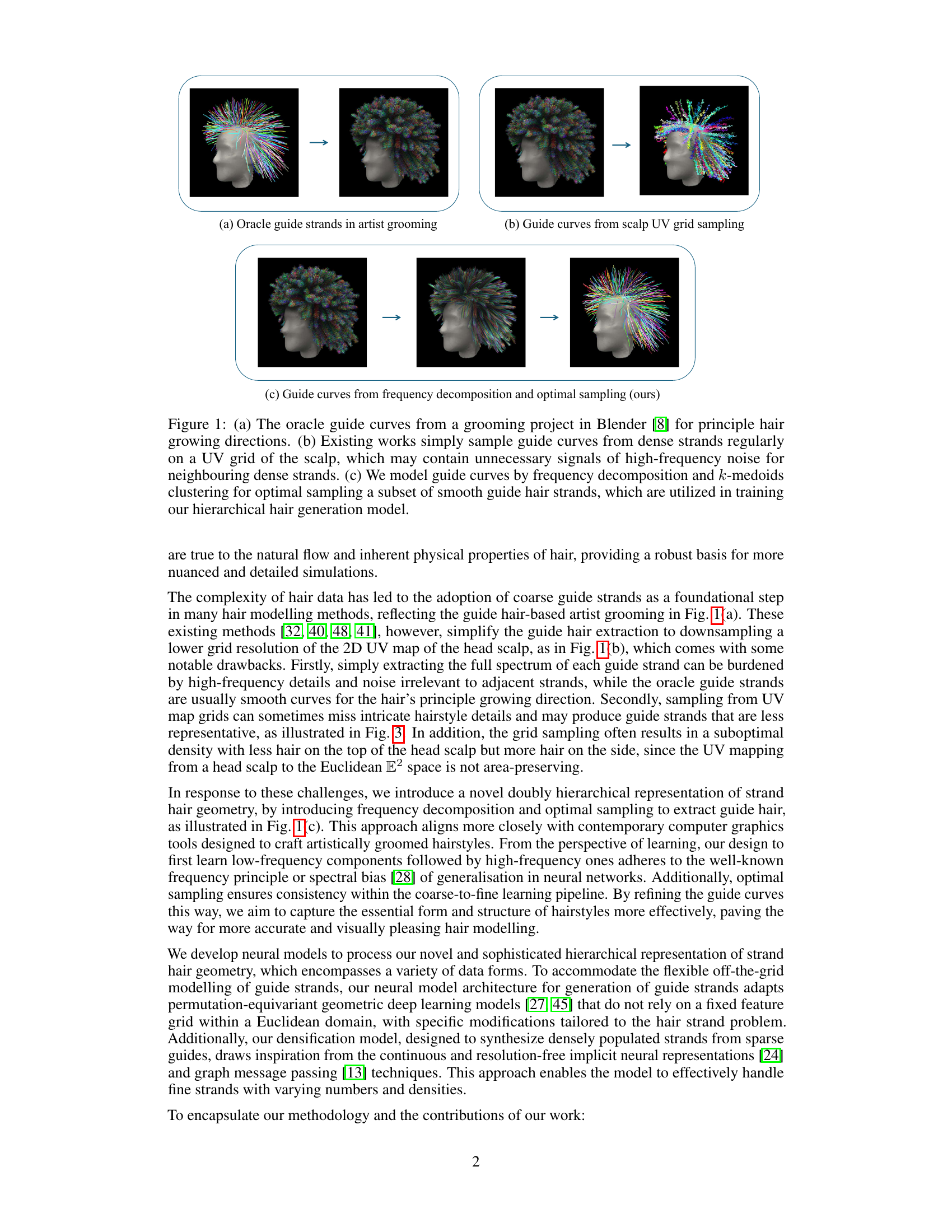
This figure compares three different approaches to generating guide curves for hair modeling. (a) Shows the ideal result from manual grooming, which is used as a reference for the comparison. (b) Shows the traditional approach of sampling from a regular grid in UV space, which may miss important details or include high-frequency noise. (c) Shows the authors’ approach, which uses frequency decomposition and k-medoids clustering to select optimal guide curves.

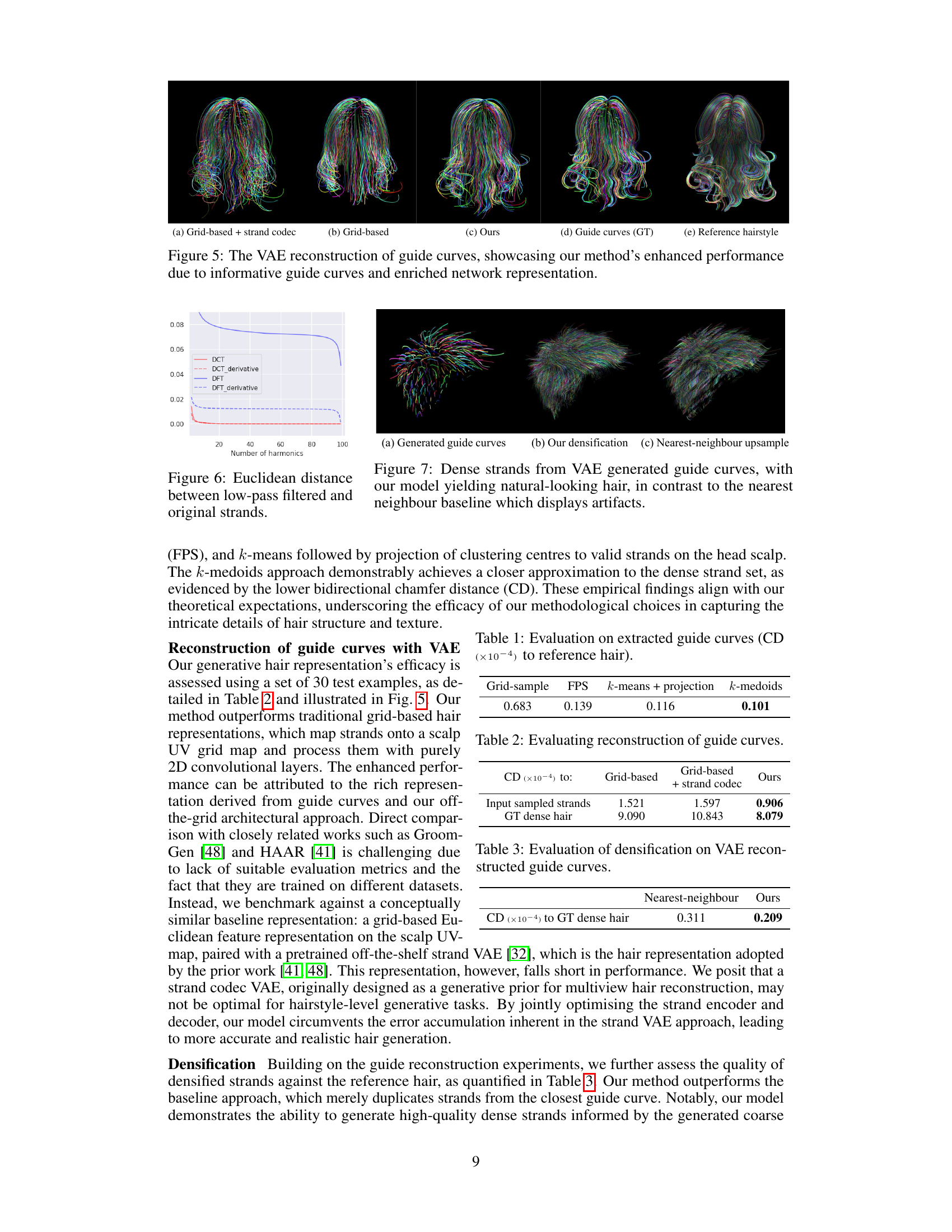
This table presents a comparison of the Chamfer Distance (CD) between the extracted guide curves using different methods (Grid-sample, FPS, k-means + projection, and k-medoids) and the reference hair. The lower the CD, the better the method is at capturing the essence and details of the original hairstyle. The results show that the k-medoids method significantly outperforms the other methods in accurately capturing the characteristics of the reference hair.
In-depth insights#
Hierarchical Hair#
A hierarchical approach to hair modeling offers significant advantages. By representing hair as a hierarchy, from coarse guide strands to fine details, we can achieve greater realism and efficiency. The coarse level captures the overall shape and flow of the hair, while finer levels add details like curls and individual strands. This hierarchical structure allows for scalable generation, where we can easily control the level of detail and the computational cost. Frequency decomposition is a crucial element, separating low-frequency structural information from high-frequency details, enabling more controlled synthesis. This multi-level approach mimics the artistic process of hair styling and offers a more intuitive and robust way to generate realistic hair. The key is to find the optimal balance between detail and computational efficiency. Challenges include handling the variability of hair types and the potential computational complexity of very dense hair, but hierarchical approaches show considerable promise for creating high-quality, computationally efficient virtual hair.
DCT Frequency#
The concept of “DCT Frequency” in the context of a research paper likely refers to the utilization of the Discrete Cosine Transform (DCT) to analyze frequency components within a signal, often applied to images or other types of data. The DCT excels at representing data with high energy compaction, meaning that a smaller number of coefficients accurately capture most of the signal’s energy. In the context of image processing or signal analysis, this is crucial as it allows for compression and efficient feature extraction. A common application might involve separating low-frequency components from high-frequency details. The low-frequency components often represent the overall structure of the image or signal, while the high-frequency components contain fine details, edges, or noise. This separation is valuable for various applications, including image compression, denoising, and feature extraction. The specific focus within the paper would determine the exact interpretation of ‘DCT Frequency’: Does it focus on the extraction of specific frequency bands, the use of DCT coefficients as features, or a comparison against other frequency analysis techniques such as FFT? Regardless, understanding the role and characteristics of DCT frequency analysis is paramount in understanding the paper’s methodology and results. The choice of DCT over other transforms such as FFT (Fast Fourier Transform) might be motivated by the handling of boundary conditions, particularly important when dealing with non-periodic data. DCT inherently addresses issues associated with discontinuities at signal boundaries, offering advantages for certain types of signals such as image data.
K-medoids Sampling#
K-medoids sampling offers a powerful technique for selecting a representative subset of data points, particularly useful when dealing with high-dimensional or complex datasets. In the context of strand-based hair modeling, k-medoids excels at identifying the most representative guide strands from a dense set. Unlike grid-based sampling, which can miss crucial details or introduce biases, k-medoids ensures that the selected guide strands accurately capture the essential features and characteristics of the entire hairstyle. The algorithm’s ability to choose actual data points (medoids) as cluster centers, rather than virtual averages, enhances interpretability and facilitates a more intuitive understanding of the selected subset. This approach aligns well with artist workflows, where stylists typically start by selecting key strands to define the overall shape before adding details. The resulting guide strands serve as an effective and efficient starting point for generating dense hair, offering a significant advantage over simpler methods. The method’s robustness and its ability to capture the underlying structure make it a valuable contribution to the field of virtual human hair generation.
VAE Generation#
The heading ‘VAE Generation’ strongly suggests the core methodology of the research paper revolves around Variational Autoencoders (VAEs). VAEs are a powerful class of generative models capable of learning complex data distributions and generating new samples resembling the training data. In this context, the VAE likely serves as the primary architecture for generating strand-based hairstyles. The paper probably details the specific VAE architecture, including encoder and decoder networks, potentially employing convolutional layers to process the spatial information inherent in hair geometry. The latent space learned by the VAE plays a crucial role, likely capturing the essential characteristics of the hairstyles. Furthermore, the discussion under this heading would delve into training procedures, loss functions (possibly including reconstruction loss and KL divergence), and techniques used to guide the generation process. The quality of generated hairstyles directly depends on the effectiveness of the VAE, highlighting the importance of network design, hyperparameter tuning, and possibly employing advanced training techniques like adversarial training or other regularization methods to improve stability and diversity of the output. The ‘VAE Generation’ section should present quantitative and qualitative results showcasing the model’s ability to generate realistic and varied hairstyles.
High-Freq Details#
The section on “High-Freq Details” in this research paper focuses on the high-frequency components of hair strands, a crucial aspect for realistic hair rendering. The authors distinguish between low-frequency structural information (the overall shape) and high-frequency details (curls, frizz, and fine variations). They utilize the Discrete Cosine Transform (DCT) to isolate these high-frequency components, demonstrating its effectiveness over the Discrete Fourier Transform (DFT) in handling open curves, which are characteristic of hair strands. A conditional Variational Autoencoder (VAE) is then employed to generate these details, conditioned on the low-frequency information previously obtained. This approach allows for a level of control and accuracy, enabling the synthesis of hair with varying degrees of curliness, volume, and overall realism. The importance of this separate handling of frequencies is underscored by the authors’ observations in traditional hair styling, where artists typically start with basic shapes and then add details incrementally. The effectiveness of the method is empirically validated by comparing visually generated hairstyles to those seen in a ground-truth dataset.
More visual insights#
More on figures

This figure compares the Discrete Cosine Transform (DCT) and Discrete Fourier Transform (DFT) methods for smoothing an example curly hair strand. It shows that DFT, which assumes periodic signals, produces artifacts (Gibbs phenomenon) at the ends of the open curve representing a hair strand, while DCT, designed for non-periodic signals, results in a smoother curve. The DCT uses fewer harmonics to effectively smooth the strand because of its energy compaction property and flexible boundary conditions.

This figure compares guide hair curves generated using two different methods: k-medoids clustering and grid sampling. The k-medoids method selects a subset of guide curves from a dense set of hair strands that best represents the overall hairstyle. The grid sampling method simply samples curves from a regular grid on the scalp. The figure shows that the k-medoids method more accurately captures the essential details and characteristics of the hairstyle compared to grid sampling, which can miss important details.
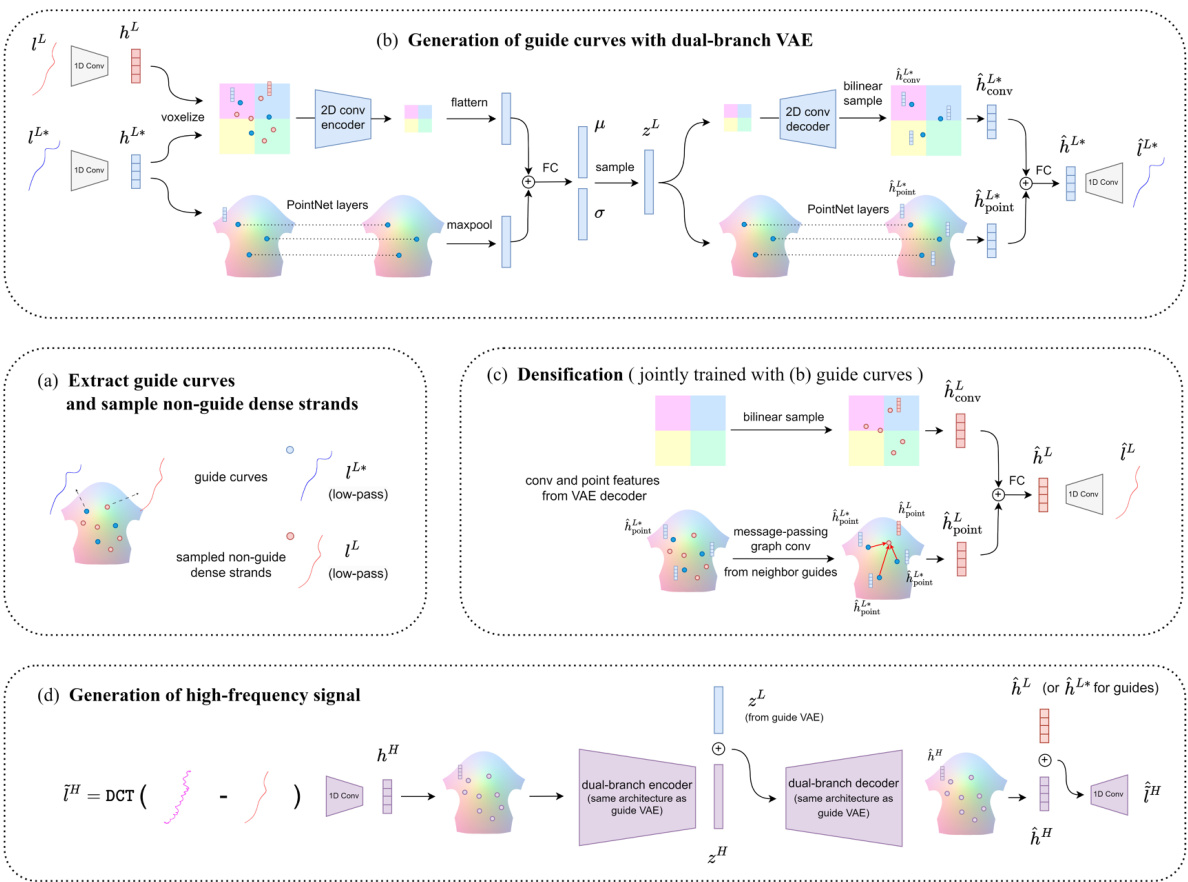
This figure shows the overall architecture of the proposed hierarchical generative model for hair strand generation. It consists of four main stages: (a) Extraction of guide curves and sampling of non-guide dense strands: low-pass filtered dense strands are used to generate optimal guide strands via k-medoids clustering. Non-guide dense strands are also sampled for training. (b) Generation of guide curves with a dual-branch VAE: a variational autoencoder (VAE) is used to generate the optimal guide curves using PointNet and 2D convolutional layers. (c) Densification (jointly trained with (b)): the densification module, jointly trained with the guide curve model, generates dense strands by aggregating features from the convolution grid and neighboring guide curves via graph convolution. (d) Generation of high-frequency signals: another dual-branch VAE refines the high-frequency details conditioned on the low-pass filtered principal strand signals.

This figure compares the VAE reconstruction of guide curves using three different methods: (a) Grid-based + strand codec, (b) Grid-based, and (c) Ours. The ground truth (GT) guide curves and reference hairstyle are also shown in (d) and (e) respectively. The results demonstrate that the proposed method (c) more accurately captures the essence and details of the original hairstyle (e), outperforming the traditional grid-based sampling methods (a) and (b). This improved performance is attributed to the use of more informative guide curves in the proposed method, which better preserve the hairstyle’s inherent characteristics.
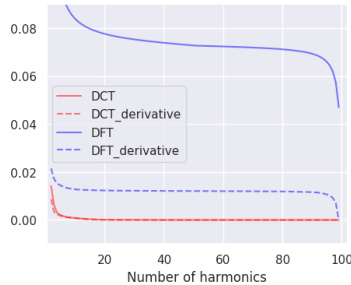
This figure compares the Euclidean distance between low-pass filtered strands and their original counterparts, using different frequency decomposition methods (DCT, DCT with derivative, DFT, DFT with derivative). The x-axis represents the number of harmonics used, while the y-axis shows the Euclidean distance. The results illustrate that DCT, especially when applied to the derivative of the strand, achieves significantly lower distance compared to DFT methods, highlighting its effectiveness in smoothing open curves like hair strands while preserving essential features.

This figure compares the results of three different methods for generating dense hair strands from a set of generated guide curves. The first image shows the generated guide curves. The second image displays the dense hair strands generated by the authors’ method, which uses a variational autoencoder (VAE) and demonstrates natural and realistic results. The third image shows the results of a simpler nearest-neighbor upsampling method, which produces noticeably less natural and more artificial-looking results because it lacks the more sophisticated modelling of the authors’ approach.

This figure illustrates the overall pipeline of the proposed hierarchical hair generation model. It shows the process in four stages: (a) Data sampling for training, (b) Generation of guide curves using a PVCNN VAE, (c) Generation of dense strands using a combination of convolutional and graph convolutional networks, and (d) Refinement of high-frequency details using another dual-branch VAE.

This figure showcases various hairstyles generated using the proposed doubly hierarchical generative model for strand-based hair. The model successfully creates diverse hairstyles with realistic and nuanced high-frequency details, demonstrating its ability to generate a wide range of styles.

This figure compares two methods for extracting guide hair curves from dense hair strands: k-medoids clustering and grid sampling. The k-medoids method selects a subset of guide curves that best represent the overall hairstyle, while grid sampling uniformly samples curves from the scalp UV map. The figure demonstrates that k-medoids preserves more important details than the grid sampling method.

This figure compares three different methods for obtaining guide curves for hair generation. (a) shows oracle guide strands from artist grooming, representing the ideal. (b) demonstrates the typical approach of sampling guide curves from a scalp UV grid, which can lead to noisy and suboptimal results. (c) presents the authors’ proposed method of using frequency decomposition and k-medoids clustering to select optimal guide strands, which better captures the hairstyle’s characteristics.
More on tables
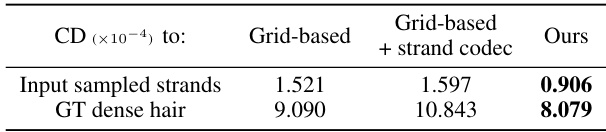
This table presents a comparison of the Chamfer distance (CD) between the reconstructed guide curves and the ground truth (GT) dense hair, for three different methods: grid-based sampling, grid-based sampling with a pre-trained strand codec, and the proposed method. The results show that the proposed method achieves significantly lower CD values, indicating a more accurate reconstruction of the guide curves compared to the baseline methods.

This table presents a comparison of the Chamfer distance (CD) between generated dense hair strands and ground truth dense hair strands using two different methods: nearest-neighbor upsampling and the proposed method. The proposed method achieves a lower CD, indicating better accuracy in generating dense strands.
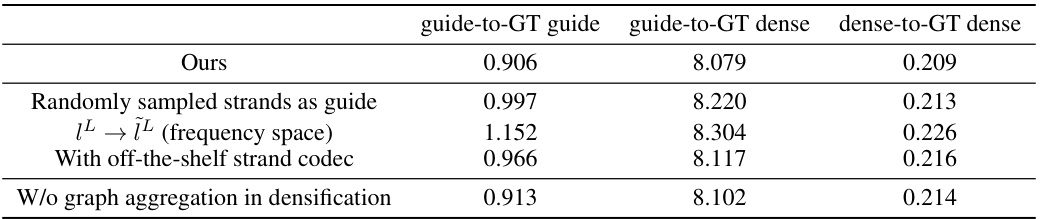
This table presents the results of ablation studies conducted to evaluate the impact of different design choices on the performance of the Variational Autoencoder (VAE) model used for reconstructing low-frequency guide curves and densifying them into dense hair strands. The metrics used are Chamfer Distance (CD), measuring the dissimilarity between the generated results and the ground truth, lower scores indicate better performance. The ablation studies involve: 1. Randomly sampled strands as guide: Replacing the k-medoids selected guide strands with randomly chosen ones. 2. ÎL → ÎL (frequency space): Using the frequency representation of strands (DCT coefficients) directly instead of converting them back to the spatial domain. 3. With off-the-shelf strand codec: Using a pre-trained strand codec instead of the proposed end-to-end training. 4. W/o graph aggregation in densification: Removing the graph convolutional network from the densification module.

This table presents the results of an ablation study on the high-frequency reconstruction part of the model. It compares the Mean Absolute Error (MAE) achieved by the proposed method against a baseline that uses an off-the-shelf strand codec in frequency space. The lower MAE indicates better performance.

This table presents the results of an ablation study on the impact of varying frequency thresholds on the reconstruction quality achieved by the Variational Autoencoder (VAE) in the paper’s model. It shows how different frequency thresholds affect the reconstruction quality of the hair strands, measured by the Chamfer Distance (CD). The lower the CD, the better the reconstruction quality.

This table presents the results of a user study comparing the realism of hairstyles generated by the proposed method and the HAAR method. Users rated the realism of 30 hairstyles generated by each method on a scale of 1 to 10, with 10 being the most realistic. The table shows the average scores for all hairstyles and also breaks down the scores by hair type (short non-curly, long non-curly, and curly).
Full paper#