Achieving Linear Convergence with Parameter-Free Algorithms in Decentralized Optimization

↗ arXiv ↗ Hugging Face

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in decentralized optimization because it presents a novel parameter-free algorithm that achieves linear convergence. This addresses a major limitation of existing methods, which often require expert knowledge for hyperparameter tuning, hindering practical application. The proposed method’s adaptivity and scalability also open new avenues for research in distributed machine learning and other relevant fields.

Visual Insights

#

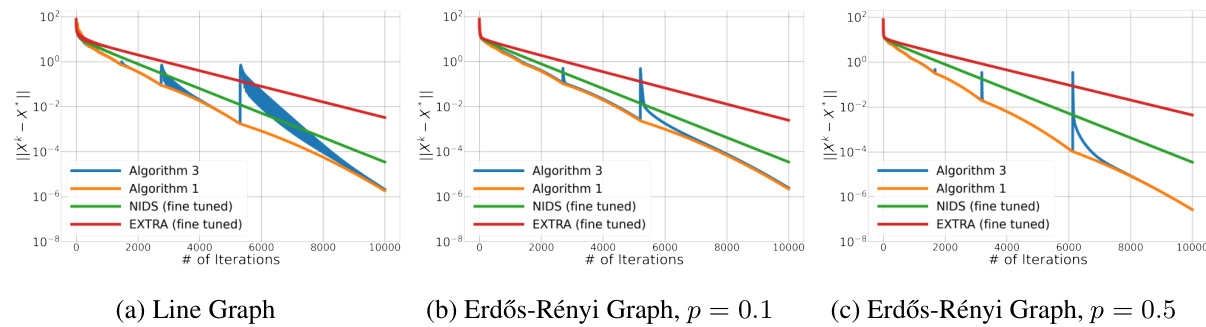
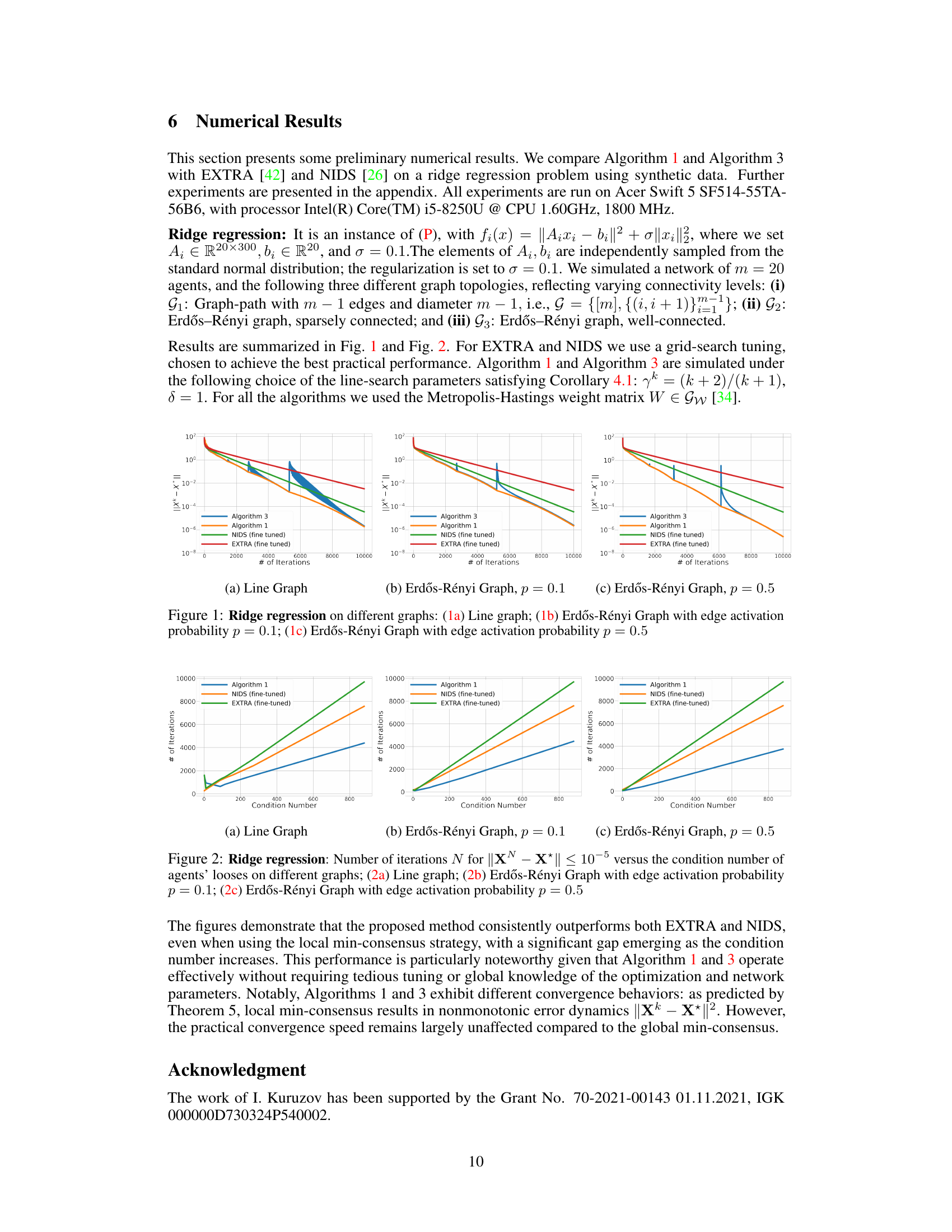
🔼 This figure compares the performance of Algorithm 1, Algorithm 3, EXTRA, and NIDS on a ridge regression problem with different graph topologies: a line graph, a sparsely connected Erdős-Rényi graph (p=0.1), and a well-connected Erdős-Rényi graph (p=0.5). The y-axis represents the objective function value, and the x-axis represents the number of iterations. The algorithms’ convergence speed and scalability are compared across different network structures.

read the caption

Figure 1: Ridge regression on different graphs: (1a) Line graph; (1b) Erdős-Rényi Graph with edge activation probability p = 0.1; (1c) Erdős-Rényi Graph with edge activation probability p = 0.5

In-depth insights

#

Adaptive Decentralized

#

Adaptive decentralized algorithms represent a significant advancement in distributed optimization, addressing the limitations of traditional methods. Adaptivity is crucial because it allows algorithms to automatically adjust to the characteristics of the underlying network and objective function, eliminating the need for manual hyperparameter tuning. This is especially important in decentralized settings where global information is often unavailable or difficult to obtain. Decentralization, on the other hand, offers robustness and scalability by distributing computation and communication across multiple agents, mitigating the risks of single points of failure. Combining adaptivity and decentralization leads to algorithms that are both efficient and resilient to changes in network topology or data distribution. However, designing such algorithms presents a significant challenge, requiring novel techniques to ensure convergence and desirable performance guarantees. Key research questions revolve around developing efficient communication strategies, handling heterogeneity in agent capabilities, and providing theoretical convergence guarantees under realistic assumptions. The development of robust and efficient adaptive decentralized algorithms holds immense potential for various applications, including large-scale machine learning, distributed control systems, and sensor networks.

Linear Convergence

#

The concept of linear convergence is central to the research paper, signifying a significant improvement over existing decentralized optimization algorithms. Instead of the slower sublinear convergence rates commonly observed, this work demonstrates that its proposed parameter-free method achieves linear convergence for strongly convex and smooth objective functions. This is a noteworthy achievement because it offers a faster convergence speed while simultaneously eliminating the need for manual tuning or prior knowledge of network or function parameters. The linear convergence rate is theoretically proven and confirmed through numerical experiments, highlighting the algorithm’s efficiency and scalability. The adaptive stepsize selection mechanism, enabled by a novel variable metric and local backtracking line-search, plays a crucial role in achieving this linear convergence without requiring global information. This feature makes the algorithm robust and suitable for practical applications where the required parameter knowledge may be unavailable or difficult to obtain. The superior performance of the proposed method compared to existing adaptive and non-adaptive techniques is a key outcome, impacting various applications relying on decentralized optimization.

Parameter-Free Methods

#

Parameter-free methods represent a significant advancement in optimization, particularly within decentralized settings. Traditional methods often necessitate meticulous tuning of hyperparameters (e.g., step sizes), requiring prior knowledge of problem characteristics (like Lipschitz constants or network connectivity). This is often impractical in decentralized scenarios where such global information is unavailable or costly to obtain. Parameter-free methods elegantly sidestep this limitation, automating parameter selection and enhancing robustness and scalability. Their adaptive mechanisms, such as line search or curvature estimation, enable the algorithm to dynamically adjust its parameters, ensuring convergence without reliance on predefined values. This is crucial for decentralized machine learning applications, where data distribution and network topology can be dynamic and unpredictable. While parameter-free methods show great promise, potential drawbacks include increased computational overhead due to the adaptive process and challenges in establishing convergence guarantees with the same theoretical rigor as traditional fixed-parameter methods. Future research may focus on optimizing these adaptive mechanisms for further efficiency, and exploring the design of parameter-free methods for increasingly complex decentralized environments.

Backtracking Line-Search

#

The concept of a backtracking line-search within the context of decentralized optimization is a crucial component for achieving parameter-free algorithms. It addresses the challenge of adaptively selecting step sizes without relying on global knowledge of network parameters or function properties. The core idea is to iteratively adjust the step size based on local information, ensuring sufficient descent in a merit function. This local approach avoids the need for conservative step size selections that are common in traditional decentralized algorithms and can lead to slow convergence or even divergence. A key aspect involves the design of a suitable merit function and a descent direction that incorporates both the local optimization landscape and the network structure. This ensures that the backtracking process effectively navigates the complexities of decentralized computation while still guaranteeing convergence. The effectiveness of the backtracking line-search hinges on its ability to balance exploration and exploitation, efficiently finding an appropriate step size that is neither too small (leading to slow convergence) nor too large (leading to oscillations or divergence). A well-designed backtracking line-search method is essential for realizing the practical potential of parameter-free decentralized optimization algorithms.

Future Research

#

Future research directions stemming from this decentralized optimization work could explore several promising avenues. One key area is improving the scalability of the proposed algorithm to handle even larger networks and higher-dimensional data, potentially through more sophisticated consensus mechanisms or distributed optimization techniques. Investigating the algorithm’s robustness to noise and communication failures in real-world network settings is another important direction. This would involve analyzing the impact of noisy gradients or intermittent communication links on convergence rates and developing adaptive strategies to mitigate these effects. Furthermore, extending the algorithm’s applicability to non-convex optimization problems is a significant challenge that warrants further investigation. While promising initial results are presented for strongly convex functions, exploring the behavior of the algorithm with non-convex functions and developing corresponding convergence guarantees is crucial. Finally, a comprehensive experimental evaluation across diverse datasets and network topologies is necessary to fully characterize the algorithm’s performance and scalability relative to existing methods, particularly in scenarios with varying levels of network connectivity and node heterogeneity. These enhancements are essential to transition this research from a theoretical foundation to a practical and widely applicable solution for large-scale decentralized optimization tasks.

More visual insights

#

More on figures

🔼 This figure shows the results of the ridge regression experiments on three different graph topologies with varying connectivity: line graph, sparse Erdős-Rényi graph (p=0.1), and well-connected Erdős-Rényi graph (p=0.5). It compares the performance of Algorithm 1 and Algorithm 3 against EXTRA and NIDS (both fine-tuned). The x-axis represents the number of iterations, and the y-axis represents the error ||X - X*||. The plots illustrate the convergence speed and scalability of the proposed algorithms compared to the existing methods.

read the caption

Figure 1: Ridge regression on different graphs: (1a) Line graph; (1b) Erdős-Rényi Graph with edge activation probability p = 0.1; (1c) Erdős-Rényi Graph with edge activation probability p = 0.5

🔼 The figure shows the results of a ridge regression experiment using three different graph topologies: a line graph, a sparsely connected Erdős-Rényi graph (p=0.1), and a well-connected Erdős-Rényi graph (p=0.5). The plots compare the performance of Algorithm 1, Algorithm 3, EXTRA (fine-tuned), and NIDS (fine-tuned) in terms of convergence speed (logarithmic scale of error vs. number of iterations). It illustrates how the proposed algorithms perform compared to existing methods under varying network connectivity.

read the caption

Figure 1: Ridge regression on different graphs: (1a) Line graph; (1b) Erdős-Rényi Graph with edge activation probability p = 0.1; (1c) Erdős-Rényi Graph with edge activation probability p = 0.5

Full paper

#