TL;DR#
Many systems are modeled using stochastic differential equations (SDEs), but learning their properties from data is challenging. Conventional methods struggle with the unbounded nature of the infinitesimal generator (IG), which describes the system’s dynamics. Accurately learning the IG is critical for understanding the system’s behavior and predicting its future states. Existing approaches suffer from the curse of dimensionality and produce unreliable spectral estimations.
This paper proposes a new learning framework based on the energy functional of the stochastic process. It uses a reduced-rank estimator in Reproducing Kernel Hilbert Spaces (RKHS) to estimate the IG’s spectrum from a single trajectory. The method incorporates physical priors and provides learning bounds that are independent of the state space dimension, ensuring accurate and reliable spectral estimation. This significantly improves the accuracy and efficiency of learning IGs from limited data, addressing limitations of current methods.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with stochastic diffusion processes. It offers novel statistical learning bounds independent of state-space dimension, addressing a major challenge in the field. The energy-based risk functional provides a new avenue for learning the infinitesimal generator, enabling more accurate estimations and opening doors for further research in diverse applications.
Visual Insights#

🔼 This figure shows several results of the proposed method and compares it to other methods on different datasets. Panel a) shows the estimation of the eigenfunction for the Langevin process with different kernel length scales. Panel d) compares the eigenvalue estimation to other methods, highlighting the spurious eigenvalues. Panel e) shows the RMSE for the CIR model with respect to the number of samples. Panel f) compares the performance of the proposed method and the CIR model on real data of US mortgage rates. Finally, panels g) and h) compare the estimation of the eigenfunctions for the Muller-Brown potential using the proposed method and transfer operator methods.
read the caption
Figure 1: a) Empirical biases s₁ = 8₁ 7₁ and estimation of the first (nontrivial) eigenfunction of the IG of a Langevin process under a four-well potential. The ground truth is shown in black, our method RRR is red and blue for two different kernel lengthscales. d) Estimation by our method (black) of the eigenvalues for the same process (red) compared to the methods in [19, 1], for which eigenvalue histogram in blue shows spuriousness. e) Prediction RMSE for the CIR model w.r.t. number of samples. f) Performance of our data-driven method and fitted CIR model on the real data of US mortgage rates. g) The second eigenfunction of a Langevin process under Muller brown potential (white level lines) with its estimation by RRR h) and Transfer Operator (TO) in e). Observe that TO fails to recover the metastable state.

🔼 This table compares the proposed method with three other kernel-based methods for learning the infinitesimal generator (IG) of stochastic diffusion processes. The comparison is made across several aspects: the range of SDEs covered, the type of risk metric used, whether the method incorporates physical priors, the ability to avoid spurious eigenvalues, the provided IG error bounds, spectral convergence rates, and time complexity.
read the caption
Table 1: Comparison to previous kernel-based works on generator learning. Sample size is n, state-space dimension is d, y is the regularization parameter of KKR and RRR and r is RRR rank parameter. Our learning bounds are derived in Theorem 2 where the parameters α, β, τ quantify the intrinsic difficulty of the problem and impact of kernel choice on learning IG.
In-depth insights#
Energy-Based Learning#
Energy-based learning presents a compelling paradigm shift in machine learning by leveraging energy functions to represent probability distributions. Instead of directly optimizing likelihoods, this approach focuses on learning the energy landscape, which implicitly defines the probability distribution. This offers several advantages: it naturally handles complex, high-dimensional data by representing distributions implicitly, allowing for flexible modeling of dependencies and potentially overcoming the curse of dimensionality. Furthermore, energy-based models offer greater flexibility in incorporating prior knowledge and inductive biases through the design of carefully crafted energy functions, thus enabling more informed and robust learning. However, energy-based learning also faces challenges such as the difficulty of ensuring proper normalization of the resulting probability distributions and the computational complexity associated with high-dimensional energy functions. Nonetheless, its ability to handle complex data, its inherent flexibility in incorporating priors, and its potential for improved generalization make energy-based learning a promising avenue for future research.
Resolvent Estimation#
Resolvent estimation, in the context of learning infinitesimal generators of stochastic diffusion processes, presents a fundamental shift from directly tackling the unbounded generator. By focusing on the resolvent, a related operator with a compact form, the challenges posed by the unbounded nature of the generator are mitigated. This approach leverages the spectral properties, ensuring that the resolvent and the generator share eigenfunctions, thus enabling spectral analysis of the diffusion process through the resolvent’s spectral decomposition. Finite sample bounds, independent of the state space dimension, become achievable due to the resolvent’s compact nature and the use of an energy-based risk functional. However, practical challenges arise in approximating the resolvent’s action on the reproducing kernel Hilbert space (RKHS). The distortion between the intrinsic metric of the diffusion process and the RKHS metric significantly impacts the accuracy of spectral estimation. Hence, the proposed framework needs to account for these distortions and incorporate them into the learning process, ensuring non-spurious spectral estimation.
Spectral Bounds#
The spectral bounds analysis in this theoretical research paper is crucial for evaluating the accuracy and reliability of the proposed method for estimating the infinitesimal generator of stochastic diffusion processes. The analysis demonstrates that the method’s performance is independent of the state space dimension, overcoming the curse of dimensionality that often plagues numerical methods. Learning bounds, expressed in terms of the operator norm error and metric distortion, quantify the impact of kernel choice and data characteristics on the accuracy of the spectral estimation. These bounds highlight the trade-off between estimation accuracy and computational complexity, emphasizing the importance of carefully selecting hyperparameters. The paper provides specific conditions under which these bounds hold, indicating a strong theoretical grounding for the method. The spectral bounds analysis showcases the approach’s robustness and highlights the potential for accurate spectral estimation even with partial knowledge of the process parameters. Finite sample bounds ensure practical applicability.
Empirical Risk#
The section on Empirical Risk in this research paper focuses on developing data-driven methods to estimate the infinitesimal generator of stochastic diffusion processes. The core challenge is the unbounded nature of the generator, requiring a novel approach that overcomes limitations of traditional techniques. A key contribution is the introduction of a new energy-based risk functional for resolvent estimation that allows for efficient learning, even with partial knowledge of the system. This functional addresses the unboundedness issue by incorporating physical priors and ensuring non-spurious spectral estimation. The authors then present empirical risk minimization strategies, using both Tikhonov regularization and rank constraints to develop estimators with strong statistical guarantees. This framework successfully addresses the inherent challenges in learning the generator, including overcoming the curse of dimensionality, and provides theoretical bounds on learning performance.
Future Directions#
Future research could explore several promising avenues. Extending the framework to handle more complex SDEs, such as those with non-constant diffusion coefficients or non-Markovian dynamics, would significantly broaden its applicability. Improving computational efficiency is crucial for scaling to high-dimensional systems and larger datasets, potentially through more efficient kernel methods or dimensionality reduction techniques. Investigating alternative risk functionals beyond the energy-based approach could lead to more robust estimators and better handle situations with incomplete prior knowledge. Finally, applying the methodology to real-world problems, such as financial modeling or climate prediction, would demonstrate its practical value and reveal potential limitations in real-world scenarios. A comprehensive comparison with other state-of-the-art techniques is also necessary to solidify the proposed method’s position and identify its strengths and weaknesses.
More visual insights#
More on figures

🔼 This figure shows several results obtained by the authors’ method and compares them to other methods or ground truth. Panel (a) shows how the empirical bias relates to eigenfunction estimations, while panel (d) illustrates the spurious eigenvalues produced by other methods but not by the authors’ approach. The CIR model prediction performance (RMSE) and comparison against real data (US mortgage rates) are shown in (e) and (f), respectively. Finally, panel (g) visualizes a comparison of eigenfunction estimates between the authors’ method, the Transfer Operator method, and ground truth, highlighting the authors’ method’s ability to capture the metastable state.
read the caption
Figure 1: a) Empirical biases S₁ = 8₁ 7₁ and estimation of the first (nontrivial) eigenfunction of the IG of a Langevin process under a four-well potential. The ground truth is shown in black, our method RRR is red and blue for two different kernel lengthscales. d) Estimation by our method (black) of the eigenvalues for the same process (red) compared to the methods in [19, 1], for which eigenvalue histogram in blue shows spuriousness. e) Prediction RMSE for the CIR model w.r.t. number of samples. f) Performance of our data-driven method and fitted CIR model on the real data of US mortgage rates. g) The second eigenfunction of a Langevin process under Muller brown potential (white level lines) with its estimation by RRR h) and Transfer Operator (TO) in e). Observe that TO fails to recover the metastable state.
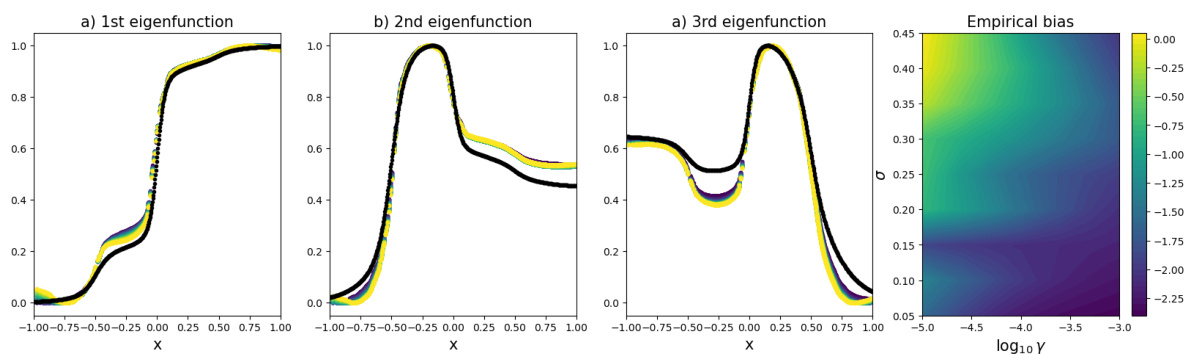
🔼 This figure demonstrates the robustness of the model’s performance across a range of hyperparameter values (µ, σ, γ). The plots (a-c) show eigenfunctions for three different modes obtained using varying µ values, comparing to the ground truth. Panel (d) visualizes the empirical bias as a heatmap, showing how it changes with respect to kernel length scale (σ) and regularization parameter (γ).
read the caption
Figure 3: Panels a)-c): Test of the model’s robustness with respect to the hyperparameter µ, tested for 30 different values between 10⁻³ and 5, compared to the ground truth result. Panel d): logarithm of the empirical bias as a function of the kernel length scale σ and the logarithm of regularization parameter γ.

🔼 This figure compares the results of the Reduced Rank Regression (RRR) method proposed in the paper against the ground truth and a Transfer Operator RRR method. Three columns show the results: ground truth, the proposed RRR method, and the transfer operator method. Each subfigure shows the results for the second and third eigenfunctions of the Muller-Brown potential. The color of each point indicates the value of the eigenfunction at that point, providing a visualization of the eigenfunctions’ shape and distribution.
read the caption
Figure 4: Results of the RRR given by our method (second column) compared to ground truth (first column) and transfer operator RRR (last column). Points are colored according to the value of the eigenfunction
Full paper#