↗ arXiv ↗ Hugging Face ↗ Hugging Face ↗ Chat
TL;DR#
Many methods align Large Language Models (LLMs) to human preferences, but often struggle to balance aligning the model’s outputs with preserving other desirable characteristics. This paper focuses on best-of-n sampling, which draws multiple samples, ranks them, and selects the top one. It tackles two main issues: understanding the relationship between this simple but effective method and other more complex alignment techniques and developing a way to efficiently train a model to directly produce samples from this best-of-n distribution.
The researchers show theoretically that best-of-n is nearly optimal in terms of aligning LLMs to human preferences while limiting undesired changes to the model’s outputs. Building on this, they propose a new alignment method called BONBON. This method directly trains a language model to match the distribution of best-of-n samples, leveraging both the best and worst samples. Experiments show that BoNBON significantly outperforms existing approaches, providing a high win-rate while maintaining off-target quality.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on LLM alignment because it introduces a novel, highly effective alignment method (BoNBON) that significantly improves win-rate while minimally affecting off-target attributes, and it provides theoretical backing for best-of-n sampling, a surprisingly effective alignment technique. The findings are widely applicable to various alignment approaches and potentially influence future research directions.
Visual Insights#
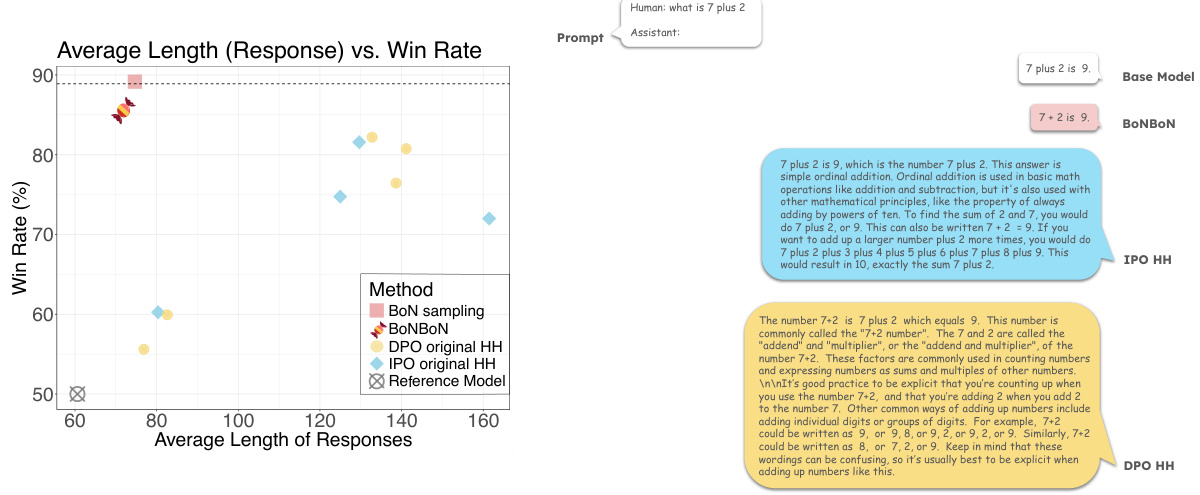
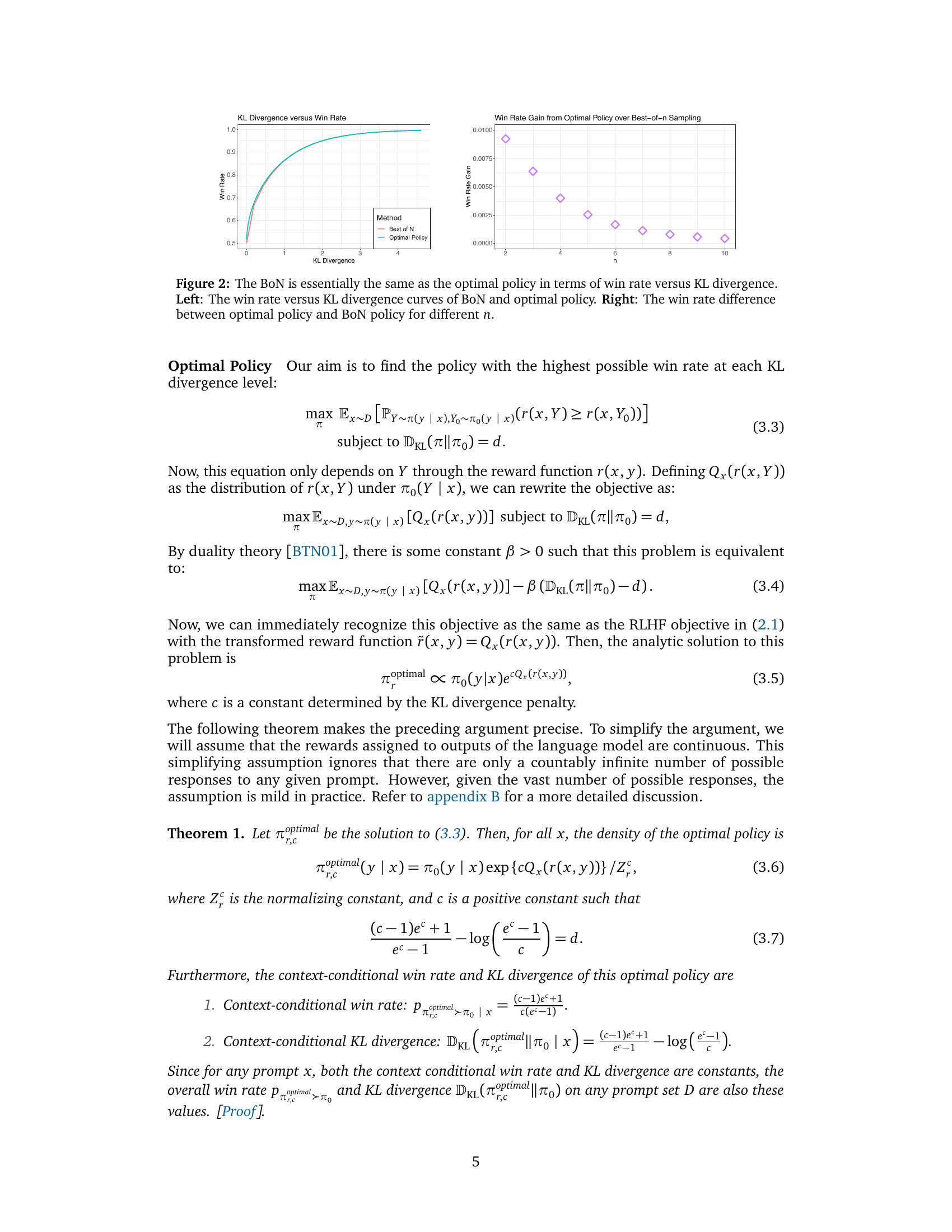
🔼 This figure shows the results of BONBON alignment compared to other methods. The left panel shows a scatter plot of average response length vs. win rate, demonstrating BONBON’s ability to achieve high win rates with minimal impact on response length. The right panel provides example responses, highlighting the difference in quality and length between BONBON and other methods.
read the caption
Figure 1: BONBON alignment achieves high win rates while minimally affecting off-target attributes of generation. Left: Average length of responses versus win rate of models aligned using each method on the Anthropic helpful and harmless single turn dialogue task, using n = 8. As predicted by theory, best-of-n achieves an excellent win rate while minimally affecting the off-target attribute length. Moreover, the BONBON aligned model effectively mimics this optimal policy, achieving a much higher win rate at low off-target drift than other alignment approaches. Right: Sample responses from models with similar win rates to BoNBON. Other methods require higher off-target deviation to achieve a comparably high win rate. We observe that this significantly changes their behavior on off-target aspects. Conversely, BONBON only minimally changes off-target behavior. See section 5 for details.

🔼 This table showcases example responses generated by different models (BONBON, DPO, and IPO) for the same prompt, all achieving similar win rates. The key observation is that BONBON, unlike the other methods, doesn’t alter the off-target attributes of the responses.
read the caption
Table 1: With similar win rates, only BoNBoN does not modify the off-target attributes. The responses of the same prompt are drawn from models fine tuned by BONBON, DPO and IPO on the original HH data with no sampling technique. The win rate of each model is around 85%.
In-depth insights#
BoN Alignment#
The concept of ‘BoN Alignment’ centers on aligning large language model (LLM) outputs with human preferences using best-of-n sampling. This method involves generating n samples, ranking them according to a reward function reflecting human preferences, and selecting the top-ranked sample. The core idea is to indirectly optimize the LLM’s distribution towards higher-reward outputs, without explicitly defining and estimating a reward model, which is the usual approach. This avoids the challenges associated with reward model misspecification and high-dimensional KL-divergence estimation. The approach offers a theoretically optimal balance between maximizing win-rate (superiority over a baseline model) and maintaining similarity to the original model’s distribution. However, the practical downside is the significant computational cost of generating multiple samples for every inference, which motivates the subsequent development of methods to directly mimic the best-of-n distribution with a fine-tuned LLM.
BoNBON Method#
The BoNBON method, as described in the paper, presents a novel approach to aligning large language models (LLMs) with human preferences. It cleverly addresses the limitations of existing alignment techniques by combining supervised fine-tuning (SFT) with an innovative contrastive learning approach. BoNBON avoids explicit KL-divergence regularization, a common pitfall of other methods that can lead to poor control over off-target attributes. Instead, BoNBON implicitly controls this trade-off by mimicking the best-of-n (BoN) sampling distribution. This is theoretically appealing because BoN is shown to be essentially optimal for balancing win-rate and minimal off-target effects. The method leverages the special structure of the BoN distribution to achieve significant improvements in alignment, demonstrating superior performance in experiments. It also tackles the high computational cost of BoN sampling by directly training the LLM to generate samples matching the BoN distribution, making it a practical and effective alignment approach.
Win-Rate Optimality#
The concept of win-rate optimality in the context of large language model (LLM) alignment centers on finding the best balance between maximizing the model’s performance (win-rate) against a baseline and minimizing the deviation from the original model. The authors frame this as an optimization problem, demonstrating that the best-of-n sampling strategy is essentially optimal within a specific class of models. This class considers the aligned model’s distribution as a tilting of the base model’s distribution, and the trade-off is investigated using KL-divergence. Best-of-n achieves a Pareto-optimal solution, maximizing win-rate for a given level of divergence. This is highly valuable because while simple to understand and implement, it provides a theoretical justification for a commonly used practical method, thus bridging the gap between theory and practice in LLM alignment. A key implication is that explicit KL regularization might be unnecessary and potentially suboptimal, as the best-of-n strategy implicitly manages the trade-off effectively without requiring the tuning of hyperparameters. However, the computational cost of best-of-n is a significant limitation, setting the stage for exploring efficient approximation methods.
Implicit KL#
The concept of “Implicit KL” in the context of large language model (LLM) alignment refers to methods that indirectly control the Kullback-Leibler (KL) divergence between the aligned model and the base model. Unlike explicit KL regularization, where a hyperparameter directly penalizes KL divergence, implicit methods achieve a similar effect through other mechanisms. For instance, best-of-n sampling implicitly biases the model towards higher-reward outputs while maintaining a degree of similarity to the original model. The paper explores this idea by demonstrating that best-of-n is essentially optimal in terms of the trade-off between win-rate and KL divergence, acting as an implicit regulator. This approach avoids the challenges associated with explicit KL regularization, such as the difficulty of accurately estimating and controlling KL divergence, particularly in high-dimensional spaces and with limited data. The authors highlight the advantage of implicit KL control in avoiding the issues of mis-estimation that can skew optimization results when explicitly aiming to minimize KL divergence. Implicit KL regularization offers a more robust and efficient pathway to LLM alignment by focusing directly on maximizing win-rate without the need to directly manipulate a potentially noisy estimate of KL divergence.
Future Work#
Future research directions stemming from this paper could explore several avenues. Extending BoNBoN’s applicability to diverse LLM architectures and tasks beyond those initially tested would significantly strengthen its generalizability and practical impact. Investigating the optimal choice of the hyperparameter α within BoNBoN, potentially through theoretical analysis or adaptive learning techniques, is crucial. A key area for improvement is mitigating the computational cost of best-of-n sampling, perhaps by developing more efficient approximation methods or exploring alternative sampling strategies that retain the benefits of best-of-n while reducing the sample count. Finally, deeper exploration into the theoretical underpinnings of BoNBoN alignment, possibly by establishing tighter bounds on its performance or analyzing its behavior under varying reward functions, would enhance understanding and potentially lead to more sophisticated alignment strategies.
More visual insights#
More on figures
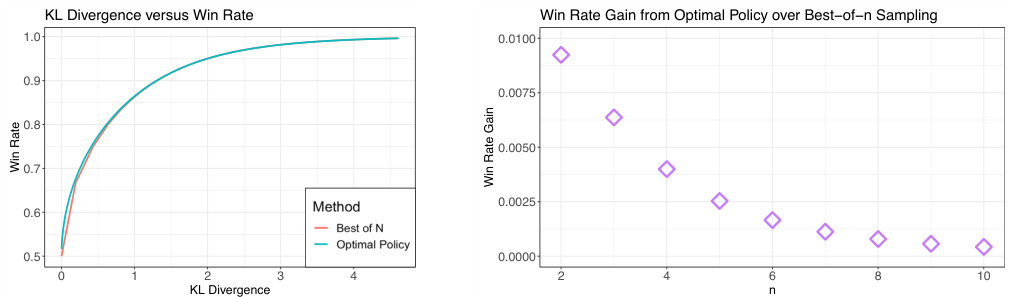
🔼 This figure shows the comparison between the best-of-n (BoN) sampling policy and the theoretically optimal policy for LLM alignment, in terms of win rate against the baseline model versus KL divergence from the baseline. The left panel shows the win-rate vs KL divergence curves for both policies, illustrating their near-equivalence. The right panel displays the win rate gain of the optimal policy over the BoN policy for different values of ’n’, the number of samples drawn. The results highlight that BoN is nearly optimal for maximizing win-rate with minimal changes to off-target aspects.
read the caption
Figure 2: The BoN is essentially the same as the optimal policy in terms of win rate versus KL divergence. Left: The win rate versus KL divergence curves of BoN and optimal policy. Right: The win rate difference between optimal policy and BoN policy for different n.

🔼 This figure demonstrates the effectiveness of BONBON alignment in achieving high win rates (percentage of times the model’s response is preferred to the base model’s response) while minimizing changes to off-target attributes such as response length. The left panel shows a plot of average response length against win rate for different alignment methods, revealing that BONBON achieves a high win rate with minimal impact on response length, as predicted by theory. The right panel provides sample responses illustrating how BONBON maintains similar off-target behavior (e.g. response quality) compared to the base model despite improving the win rate significantly more than other methods.
read the caption
Figure 1: BONBON alignment achieves high win rates while minimally affecting off-target attributes of generation. Left: Average length of responses versus win rate of models aligned using each method on the Anthropic helpful and harmless single turn dialogue task, using n = 8. As predicted by theory, best-of-n achieves an excellent win rate while minimally affecting the off-target attribute length. Moreover, the BONBON aligned model effectively mimics this optimal policy, achieving a much higher win rate at low off-target drift than other alignment approaches. Right: Sample responses from models with similar win rates to BoNBON. Other methods require higher off-target deviation to achieve a comparably high win rate. We observe that this significantly changes their behavior on off-target aspects. Conversely, BONBON only minimally changes off-target behavior. See section 5 for details.

🔼 This figure shows the results of BONBON alignment compared to other methods. The left panel shows that BONBON achieves a high win rate while maintaining similar average response length compared to the baseline model. The right panel illustrates example responses, demonstrating BONBON’s ability to maintain off-target behavior while achieving a high win rate, unlike other methods.
read the caption
Figure 1: BONBON alignment achieves high win rates while minimally affecting off-target attributes of generation. Left: Average length of responses versus win rate of models aligned using each method on the Anthropic helpful and harmless single turn dialogue task, using n = 8. As predicted by theory, best-of-n achieves an excellent win rate while minimally affecting the off-target attribute length. Moreover, the BONBON aligned model effectively mimics this optimal policy, achieving a much higher win rate at low off-target drift than other alignment approaches. Right: Sample responses from models with similar win rates to BoNBON. Other methods require higher off-target deviation to achieve a comparably high win rate. We observe that this significantly changes their behavior on off-target aspects. Conversely, BONBON only minimally changes off-target behavior. See section 5 for details.

🔼 This figure demonstrates the effectiveness of BONBON alignment in achieving high win rates (model preferred over baseline) while minimizing changes in off-target attributes (response length in this example). The left panel shows a scatter plot comparing average response length and win rate for different alignment methods. The right panel showcases example responses, highlighting how BONBON produces high-quality responses with minimal impact on other attributes, unlike other methods. The Anthropic helpful and harmless single-turn dialogue task was used with n=8 samples.
read the caption
Figure 1: BONBON alignment achieves high win rates while minimally affecting off-target attributes of generation. Left: Average length of responses versus win rate of models aligned using each method on the Anthropic helpful and harmless single turn dialogue task, using n = 8. As predicted by theory, best-of-n achieves an excellent win rate while minimally affecting the off-target attribute length. Moreover, the BONBON aligned model effectively mimics this optimal policy, achieving a much higher win rate at low off-target drift than other alignment approaches. Right: Sample responses from models with similar win rates to BoNBON. Other methods require higher off-target deviation to achieve a comparably high win rate. We observe that this significantly changes their behavior on off-target aspects. Conversely, BONBON only minimally changes off-target behavior. See section 5 for details.
More on tables

🔼 This table showcases example responses generated by different LLM alignment methods (Reference, BONBON, DPO original HH, IPO original HH, DPO BON, IPO BON) in response to the prompt: ‘what are some valentine day pranks?’ The responses highlight the varying approaches to alignment and their effects on the model’s output. BONBON, DPO BON, and IPO BON all used best-of-8 samples during training, influencing their responses.
read the caption
Table 2: More responses from different models. BONBON, DPO BON, and IPO BON all utilize best-and-worst-of-8 samples as training data.

🔼 This table shows example responses generated by different language models for the prompt: ‘Is the world flat or round?’ The models compared are a reference model, BONBON (Best-of-n), DPO (Direct Preference Optimization), and IPO (Indirect Preference Optimization). All three models used best-and-worst-of-8 samples during training. The responses highlight the varying levels of factual accuracy and the different styles of responses generated by each model.
read the caption
Table 3: More responses from different models. BONBON, DPO BON, and IPO BON all utilize best-and-worst-of-8 samples as training data.

🔼 This table shows example responses generated by different models (Reference, BONBON, DPO original HH, IPO original HH, DPO BON, IPO BON) to a prompt about cheating at poker. The models are compared to show the different responses generated by each model in relation to ethics and strategy. All the BON models utilized best-and-worst-of-8 samples as training data.
read the caption
Table 4: More responses from different models. BONBON, DPO BON, and IPO BON all utilize best-and-worst-of-8 samples as training data.

🔼 This table showcases example responses generated by different models for the prompt: ‘Is it safe to eat fish from a river in my city?’ The models compared are a reference model, BONBON (a model trained using the BONBON alignment method), DPO original HH (Direct Preference Optimization trained on the original Helpful and Harmless dataset), IPO original HH (Inverse Propensity Optimization trained on the original Helpful and Harmless dataset), DPO BON (Direct Preference Optimization trained on best-of-n samples), and IPO BON (Inverse Propensity Optimization trained on best-of-n samples). The responses highlight the varying levels of detail, safety considerations, and adherence to human preferences exhibited by each model.
read the caption
Table 5: More responses from different models. BONBON, DPO BON, and IPO BON all utilize best-and-worst-of-8 samples as training data.

🔼 This table showcases example responses generated by different language models, including the baseline model and models trained using BONBON, DPO BON, and IPO BON methods. Each model was trained using the best-and-worst responses from 8 samples. The table aims to illustrate the differences in model output quality and style as a result of different training approaches. The prompts are designed to assess the models’ ability to generate appropriate and harmless responses.
read the caption
Table 2: More responses from different models. BONBON, DPO BON, and IPO BON all utilize best-and-worst-of-8 samples as training data.
Full paper#