↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Reinforcement learning (RL) faces the ‘curse of dimensionality’ when dealing with large state and action spaces. Many real-world systems, however, possess hidden low-rank structures that, if exploited, can drastically improve RL efficiency. Current approaches often rely on strong assumptions like matrix incoherence and require prior knowledge of the structure. This limits their applicability and practicality.
This paper introduces LoRa-PI, a model-free RL algorithm that addresses these limitations. LoRa-PI employs a novel two-phase low-rank matrix estimation procedure (LME) that actively samples matrix entries based on estimated leverage scores. Crucially, LME provides entry-wise guarantees without relying on matrix incoherence, only on its spikiness. LoRa-PI uses LME for policy evaluation, alternating between policy improvement and evaluation steps. The paper proves LoRa-PI learns an ε-optimal policy with a sample complexity that depends only on the number of actions and is order-optimal, achieving significant statistical gains over existing methods.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in reinforcement learning and matrix estimation. It offers a novel, model-free algorithm (LoRa-PI) that leverages low-rank latent structures in MDPs, significantly improving sample efficiency. This is highly relevant to the current trend of improving RL performance in high-dimensional spaces. The parameter-free nature and entry-wise guarantees of the proposed method are groundbreaking, opening exciting new avenues for efficient RL algorithm design.
Visual Insights#
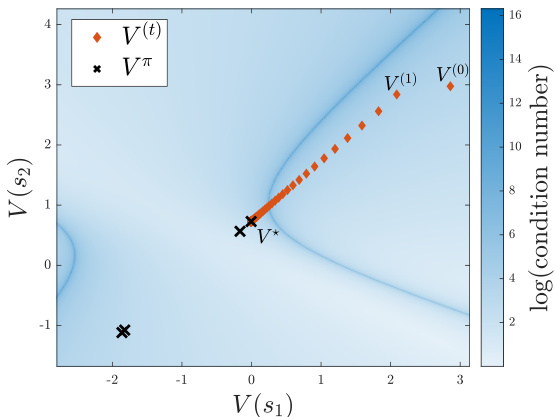
This figure compares policy iteration and value iteration for a simple MDP with two states and two actions. Policy iteration only requires bounding the condition number of a small, fixed set of matrices, while value iteration requires bounding the condition number of a much larger, unpredictable set of matrices. The background color shows the condition number, illustrating how value iteration may encounter matrices with very high condition numbers during the process.

This table compares several low-rank matrix estimation methods that provide entry-wise error guarantees. It highlights the differences in their sampling strategies (adaptive, uniform, apriori fixed anchors), the assumptions made (bounded spikiness, incoherence, noiseless), and their resulting sample complexities. LME, the method proposed in this paper, stands out for its adaptive sampling, milder assumption (bounded spikiness), and order-optimal sample complexity. The table shows that existing methods either require strong incoherence assumptions or have complexities that are not order-optimal.
In-depth insights#
Leveraged Estimation#
Leveraged estimation techniques significantly enhance the efficiency of low-rank matrix estimation by strategically focusing on the most informative data points. Leverage scores, which quantify the importance of each row and column, guide this process. By initially sampling entries based on leverage scores, then sampling additional entries from the most influential rows and columns, leveraged estimation drastically reduces the sample complexity compared to uniform sampling. This two-phase approach, combined with a CUR-like method, provides entry-wise error guarantees that remarkably do not depend on the matrix’s coherence but only on its spikiness. This is particularly advantageous for reinforcement learning, where the coherence assumption can be restrictive and the resulting improvement in sample complexity translates to improved efficiency of policy learning algorithms.
LoRa-PI Algorithm#
The LoRa-PI (Low-Rank Policy Iteration) algorithm presents a novel approach to reinforcement learning in systems with low-rank latent structures. Its model-free nature is a key advantage, eliminating the need for prior knowledge of the system dynamics. The algorithm cleverly alternates between policy evaluation and improvement steps. Policy evaluation utilizes a sophisticated two-phase leveraged matrix estimation (LME) method. This LME efficiently estimates the low-rank value function matrix by strategically sampling entries based on leverage scores, offering entry-wise error guarantees that are remarkably independent of matrix coherence, relying instead on spikiness. This adaptive sampling drastically reduces the sample complexity compared to uniform sampling approaches, resulting in order-optimal sample complexity in terms of states, actions, and desired accuracy. The overall efficiency of LoRa-PI stems from the synergy between its model-free design, the innovative LME, and the policy iteration framework. This algorithm demonstrates the potential for significant gains in sample efficiency in large-scale reinforcement learning problems with latent low-rank structures.
Sample Complexity#
The sample complexity analysis is a crucial aspect of the research paper, determining the number of samples needed to achieve a desired level of accuracy in reinforcement learning. The authors demonstrate order-optimal sample complexity, meaning their algorithm’s sample requirements scale as efficiently as theoretically possible with respect to the key factors (number of states, actions, and accuracy). A significant achievement is the dependence on matrix spikiness rather than coherence, implying the algorithm’s effectiveness even on matrices where existing methods struggle. This is coupled with parameter-free operation, removing the need for prior knowledge about the matrix structure. Entry-wise error guarantees provide fine-grained control and a stronger result than previous spectral or Frobenius norm approaches. The milder conditions required and the achieved order-optimality suggest a substantial improvement over existing reinforcement learning techniques in the context of low-rank latent structures.
Low-Rank MDPs#
Research on low-rank Markov Decision Processes (MDPs) focuses on leveraging latent structures to overcome the curse of dimensionality in reinforcement learning. Low-rank assumptions, such as low-rank transition matrices or reward functions, significantly reduce the sample complexity needed for learning optimal policies. Several approaches exist, often involving dimensionality reduction techniques like feature extraction or matrix factorization to reveal this underlying structure. However, a key challenge lies in identifying these low-rank structures effectively, especially when dealing with unknown or hidden latent factors. Algorithms often rely on computationally expensive oracles, such as empirical risk minimizers, limiting applicability. An area of active exploration is developing efficient model-free algorithms that can learn and exploit these low-rank properties without requiring prior knowledge of the underlying structure or access to strong computational oracles. Furthermore, many existing methods require restrictive assumptions like incoherence or small discount factors, which may not hold in real-world scenarios. Thus, developing robust and assumption-free methods for learning in low-rank MDPs remains a central focus of ongoing research.
Future Directions#
Future research could explore several promising avenues. Extending the low-rank assumption to more general settings is crucial, moving beyond strict low-rank structures to handle approximate low-rankness or situations where low-rankness manifests only in specific subspaces. Developing more sophisticated sampling strategies to further reduce sample complexity and improve the efficiency of leverage score estimation, potentially leveraging ideas from active learning or adaptive sampling schemes, is another key area. Improving the scalability of the algorithms to handle larger-scale MDPs is necessary for real-world applications. This might involve exploring distributed or parallel computing approaches, or designing more efficient low-rank matrix estimation methods. Theoretical analysis could focus on relaxing some of the restrictive conditions currently assumed, such as bounded spikiness or the absence of matrix coherence. This would broaden the applicability and practical impact of these methods. Finally, thorough empirical evaluation on a wider range of benchmark MDPs is critical to validate the algorithm’s performance and robustness in various scenarios. This should include testing with continuous state/action spaces, different reward structures, and tasks with varying levels of difficulty.
More visual insights#
More on figures
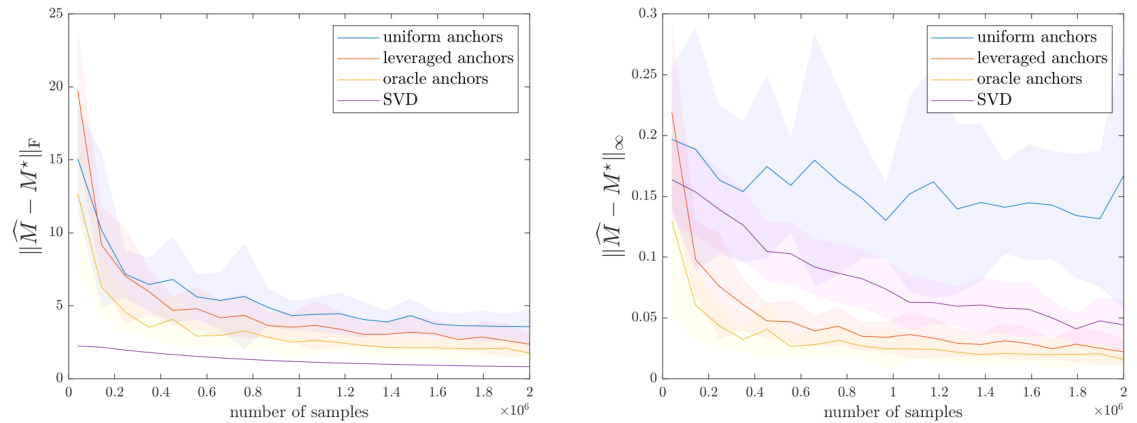
This figure compares four different matrix completion methods: uniform anchors, leveraged anchors, oracle anchors, and SVD. The methods are evaluated based on Frobenius norm and infinity norm. The results show that leveraged anchors provide better performance than uniform anchors and comparable results to oracle anchors, which have prior knowledge of the best anchors.

This figure compares the performance of value iteration (VI) and policy iteration (PI) algorithms using two different anchor selection methods: leveraged anchors (based on estimated leverage scores) and uniform anchors. The plots show the entrywise error between the estimated Q matrix (Q(t)) and the true Q* matrix at each iteration (t). The results demonstrate that leveraging anchor selection significantly improves the accuracy and reduces the entrywise error compared to uniform anchor selection, highlighting the benefit of adaptive sampling based on leverage scores.

This figure compares the performance of value iteration (VI) and policy iteration (PI) using different anchor selection methods for low-rank matrix estimation. It shows how leverage scores (quantifying information) improve the accuracy of the methods compared to uniform random selection of anchors in each iteration. The experiment uses a low-rank matrix with 70 states and 50 actions, a discount factor of 0.9 and a noise level of 0.01. The number of samples is increased geometrically in each iteration.

This figure compares the performance of three different value iteration methods in estimating a low-rank value matrix Q*. LoRa-VI with leveraged anchors uses leverage scores to select informative samples, while LoRa-VI with uniform anchors samples uniformly. The full-matrix VI serves as a baseline, using all entries. The results indicate that using leverage scores for anchor selection significantly improves estimation accuracy.

The figure shows the performance of three different value iteration methods for low-rank MDPs. The x-axis represents the total number of samples used, and the y-axis shows the error in estimating the value matrix Q*. The three methods compared are VI with leveraged anchors, VI with uniform anchors, and full-matrix VI. The results show that VI with leveraged anchors achieves significantly better performance than the other methods, demonstrating the effectiveness of the leveraged sampling approach. The results are averaged over multiple simulations and show error bars to indicate the variability in performance.
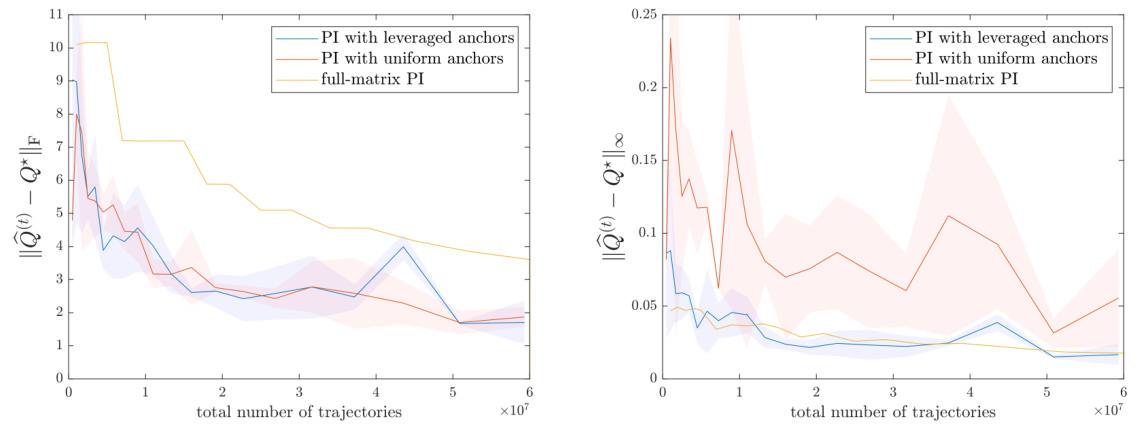
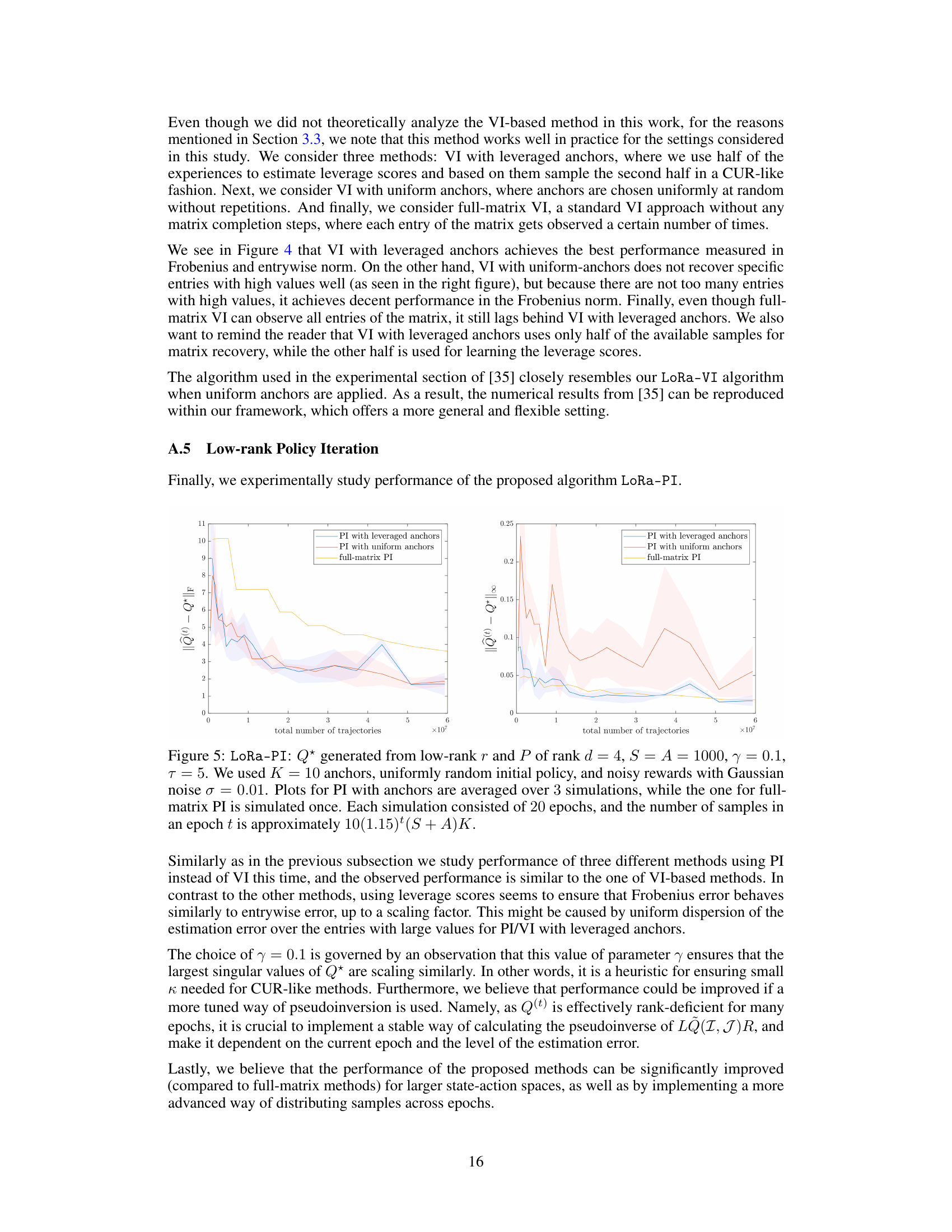
This figure shows the performance of three different policy iteration methods: PI with leveraged anchors, PI with uniform anchors, and full-matrix PI. The plot compares the Frobenius norm and entrywise error of the estimated Q-matrix against the true Q*-matrix, as the total number of trajectories increases. Leveraged anchors significantly improve the estimation accuracy compared to uniform anchors and the full-matrix method.
Full paper#