↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Reinforcement learning often struggles with data efficiency when evaluating multiple General Value Functions (GVFs) simultaneously, especially using off-policy methods with fixed behavior policies. Existing methods either rely on inefficient fixed policies or pre-collected data, leading to high variance in return estimations and inaccurate GVF predictions. This problem becomes more pronounced as the number of GVFs increases, making it computationally expensive and challenging to obtain reliable estimates.
This paper introduces GVFExplorer, a novel method that adaptively learns a single behavior policy to efficiently gather data for multiple GVFs. GVFExplorer minimizes the total variance in return across all GVFs, directly reducing the required environmental interactions. Theoretically, each behavior policy update guarantees a non-increase in overall mean squared error (MSE). Experiments in tabular, non-linear, and continuous control environments showcase significant performance improvements compared to several baselines, demonstrating the effectiveness of GVFExplorer in optimizing data usage and reducing prediction errors across multiple GVFs.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on reinforcement learning and multi-objective optimization. It introduces a novel, data-efficient approach to learning multiple General Value Functions (GVFs) in parallel, a significant challenge in current RL research. The adaptive behavior policy proposed not only improves the accuracy of GVF estimation but also opens avenues for more efficient exploration in complex, real-world scenarios.
Visual Insights#

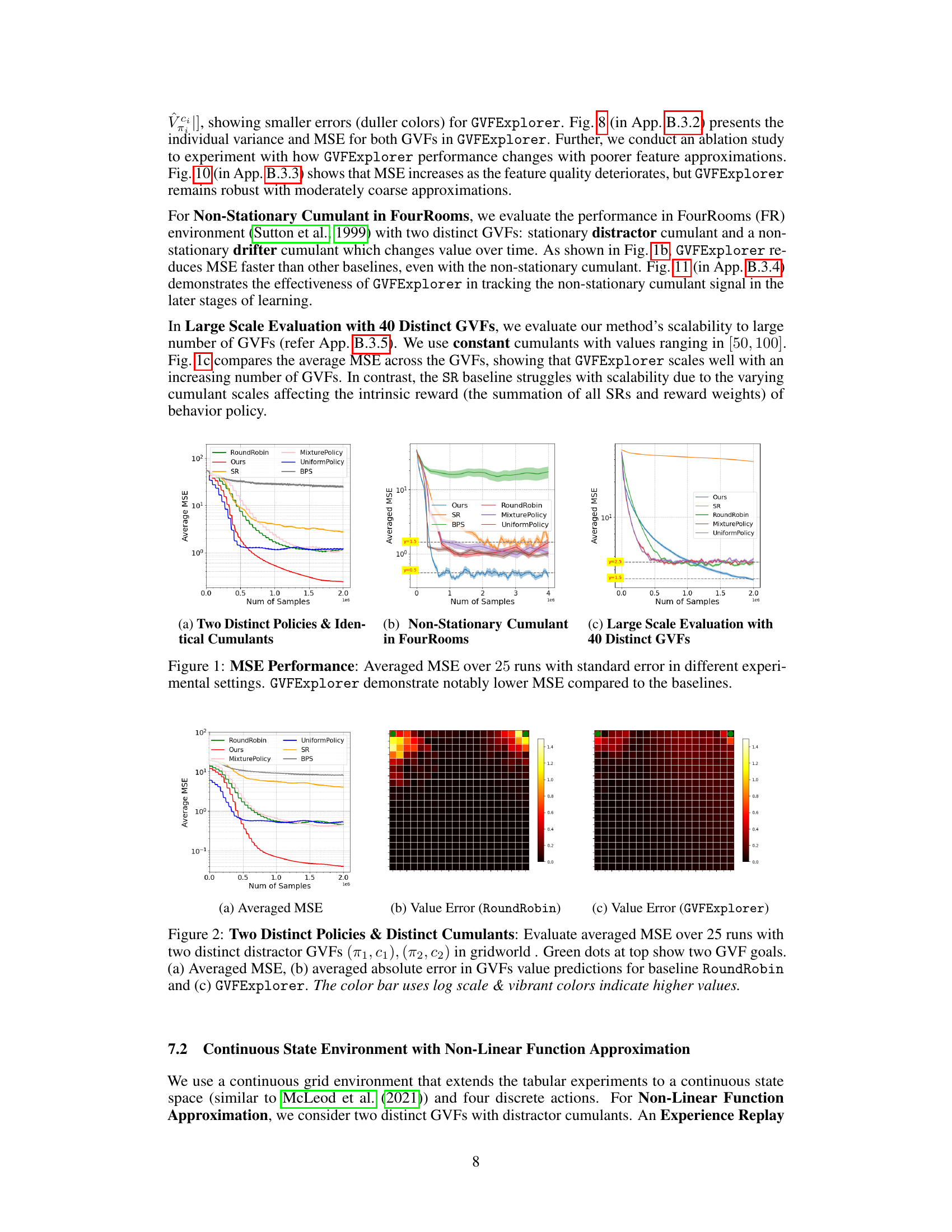
This figure displays the averaged Mean Squared Error (MSE) over 25 runs for different algorithms across three distinct experimental settings. The x-axis represents the number of samples and the y-axis shows the MSE. Each subplot corresponds to a different experimental setup: (a) Two Distinct Policies & Identical Cumulants, (b) Non-Stationary Cumulant in FourRooms, and (c) Large Scale Evaluation with 40 Distinct GVFs. The results clearly indicate that the GVFExplorer algorithm consistently outperforms all baseline methods in terms of achieving significantly lower MSE values across all three experiments.

This table compares the average Mean Squared Error (MSE) across multiple General Value Functions (GVFs) for different experimental settings using a tabular environment. It compares the performance of the proposed GVFExplorer algorithm against several baseline methods (BPS, SR, UniformPol, RoundRobin, MixPol) after 2 million learning steps. The table highlights the percentage improvement achieved by GVFExplorer compared to the best-performing baseline. Lower MSE values indicate better performance.
In-depth insights#
GVF Exploration#
Exploring General Value Functions (GVFs) presents a unique challenge in reinforcement learning due to the need for efficient data collection when evaluating multiple GVFs simultaneously. Standard approaches often struggle with data efficiency, relying on fixed behavior policies or pre-collected datasets that may not adequately cover the state-action space relevant to all GVFs. Adaptive exploration strategies offer a compelling solution by learning a single behavior policy that efficiently gathers data for all GVFs. Such a policy should ideally minimize the total variance across all GVFs, leading to more accurate predictions with fewer interactions. The design of such a policy requires careful consideration of the trade-off between exploration (sampling high-variance state-action pairs) and exploitation (focusing on areas where value estimates are already relatively certain). Methods that utilize variance estimators to guide the behavior policy update offer a promising path towards data-efficient GVF exploration, allowing for the iterative improvement of the behavior policy based on ongoing learning.
Adaptive Policy#
An adaptive policy, in the context of reinforcement learning, particularly concerning General Value Functions (GVFs), dynamically adjusts its behavior based on the current learning goals. Unlike fixed policies, which remain constant, an adaptive policy continuously learns and refines its action selection strategy. This adaptation is crucial for data-efficient learning of multiple GVFs because it allows the agent to focus on exploring states and actions that are particularly uncertain, thereby reducing the need for extensive environmental interaction. The adaptive policy is typically designed to minimize the total variance of the return across multiple GVFs, effectively lowering the mean squared error in predictions. This approach is particularly useful when learning many GVFs in parallel, as a fixed strategy would struggle to provide sufficient data for all target policies. Therefore, an adaptive policy represents a significant improvement over traditional approaches, improving learning efficiency, data usage, and prediction accuracy. It tackles the exploration-exploitation dilemma inherent in reinforcement learning, efficiently balancing the need to explore unfamiliar parts of the state-action space with the need to exploit already-known high-reward areas to optimize the overall MSE of the GVFs.
Variance Reduction#
Variance reduction is a crucial concept in many areas of research, particularly in machine learning and statistics, aiming to enhance the efficiency and accuracy of estimations by minimizing the variability in results. Effective variance reduction techniques can significantly reduce the amount of data required to achieve a certain level of accuracy, making them especially valuable when data collection is expensive or time-consuming. In the context of reinforcement learning, where agents interact with environments to learn optimal policies, variance reduction is critical for efficient learning. Methods for reducing variance often involve careful sampling strategies, such as importance sampling, or the use of control variates. These techniques aim to select data points that provide the most informative insights, reducing the influence of noisy or less-relevant observations. The goal is to improve the reliability of estimates and accelerate the convergence of learning algorithms, ultimately leading to improved performance and generalization. The choice of a suitable variance reduction technique will depend on the specific application and the nature of the data, requiring a careful consideration of the trade-offs between computational complexity and the magnitude of variance reduction achieved.
Mujoco Results#
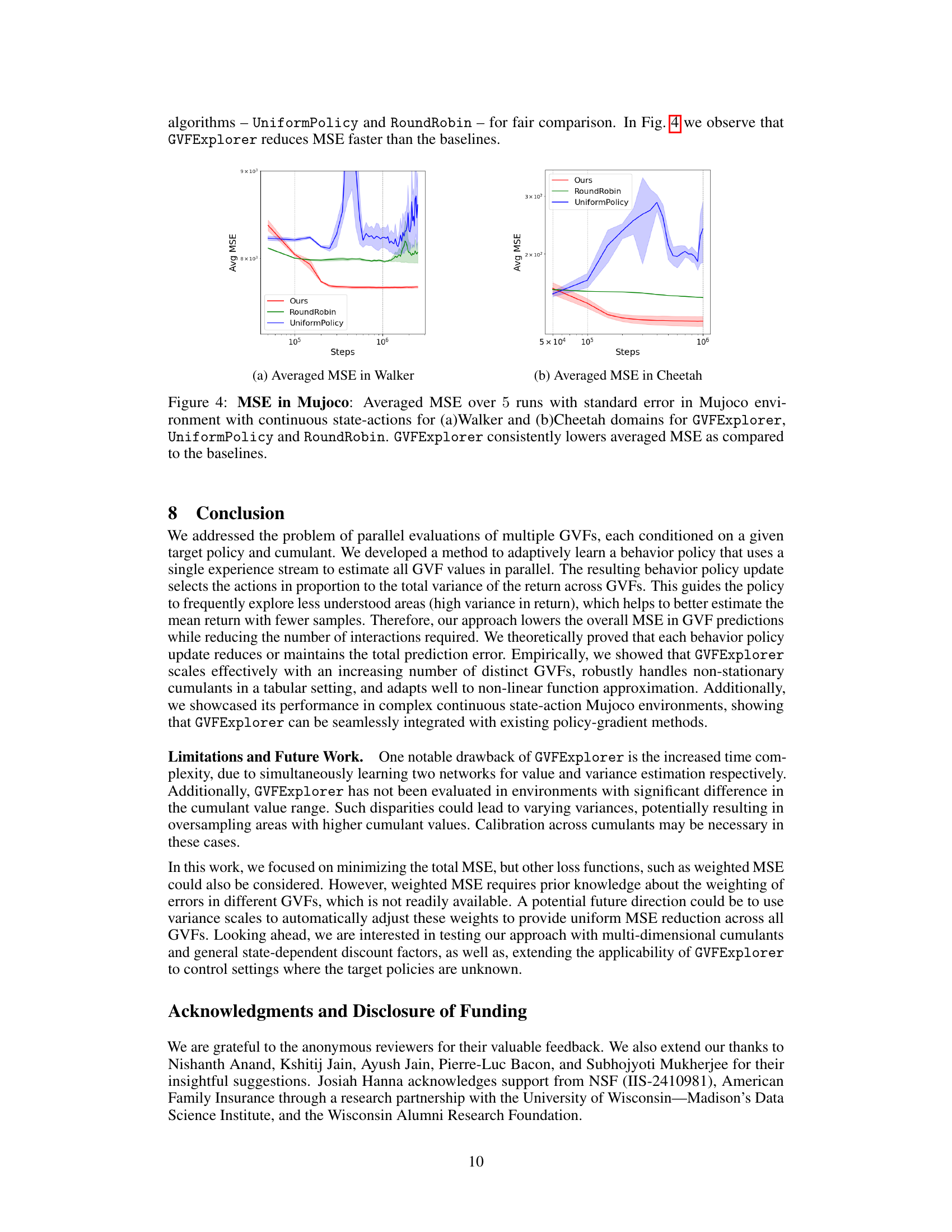
In a MuJoCo environment, the study evaluates the GVFExplorer algorithm’s performance on continuous state-action tasks using the Walker and Cheetah domains. Two distinct GVFs (‘walk’ and ‘flip’ for Walker, ‘walk’ and ‘run’ for Cheetah) are defined to assess the algorithm’s ability to handle diverse tasks. A policy gradient method (Soft Actor-Critic or SAC) is integrated to accommodate the continuous action space. Results indicate that GVFExplorer consistently outperforms baselines (UniformPolicy and RoundRobin) in reducing mean squared error (MSE), showcasing its effectiveness in data-efficient multi-objective learning in complex, continuous environments. This is particularly notable as MuJoCo simulations present significant challenges due to their high dimensionality and non-linear dynamics. The use of KL regularization to prevent divergence from target GVFs further highlights the algorithm’s robustness. The inclusion of PER (Prioritized Experience Replay) further improved performance in some aspects, illustrating the complementary nature of exploration strategies and data prioritization for efficient learning.
Future Works#
Future work for this research could explore several promising avenues. Extending the approach to handle more complex reward functions and environments is crucial, particularly those with non-stationary or multi-modal reward signals, and investigating the effects of different function approximation techniques on the overall performance is important. Additionally, developing a more robust variance estimator to deal with the challenges of off-policy learning and high-dimensional state spaces is important. This would enhance the accuracy and efficiency of the GVFExplorer algorithm. Further theoretical analysis focusing on the convergence rates and stability properties of the behavior policy updates could provide deeper insights into the algorithm’s workings. Finally, it would be beneficial to evaluate the approach on a wider range of real-world tasks and applications, such as personalized recommender systems or robotics control problems, to demonstrate its practical value and scalability.
More visual insights#
More on figures

This figure compares the Mean Squared Error (MSE) performance of the proposed GVFExplorer algorithm against several baseline methods across three different experimental scenarios. The x-axis represents the number of samples used, and the y-axis shows the average MSE across all GVFs (General Value Functions). The three subfigures showcase different experimental settings: (a) Two Distinct Policies & Identical Cumulants, (b) Non-Stationary Cumulant in FourRooms, and (c) Large Scale Evaluation with 40 Distinct GVFs. In all cases, GVFExplorer consistently outperforms the baselines, demonstrating its effectiveness in learning multiple GVFs efficiently and accurately.
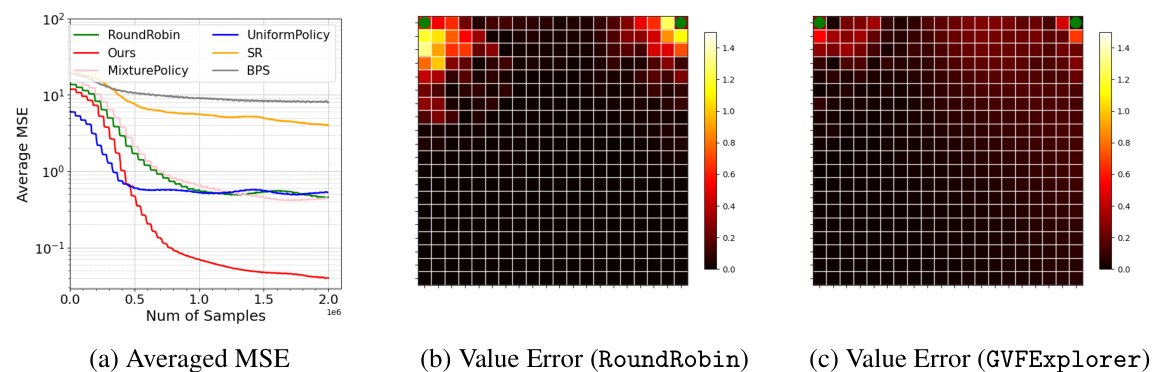
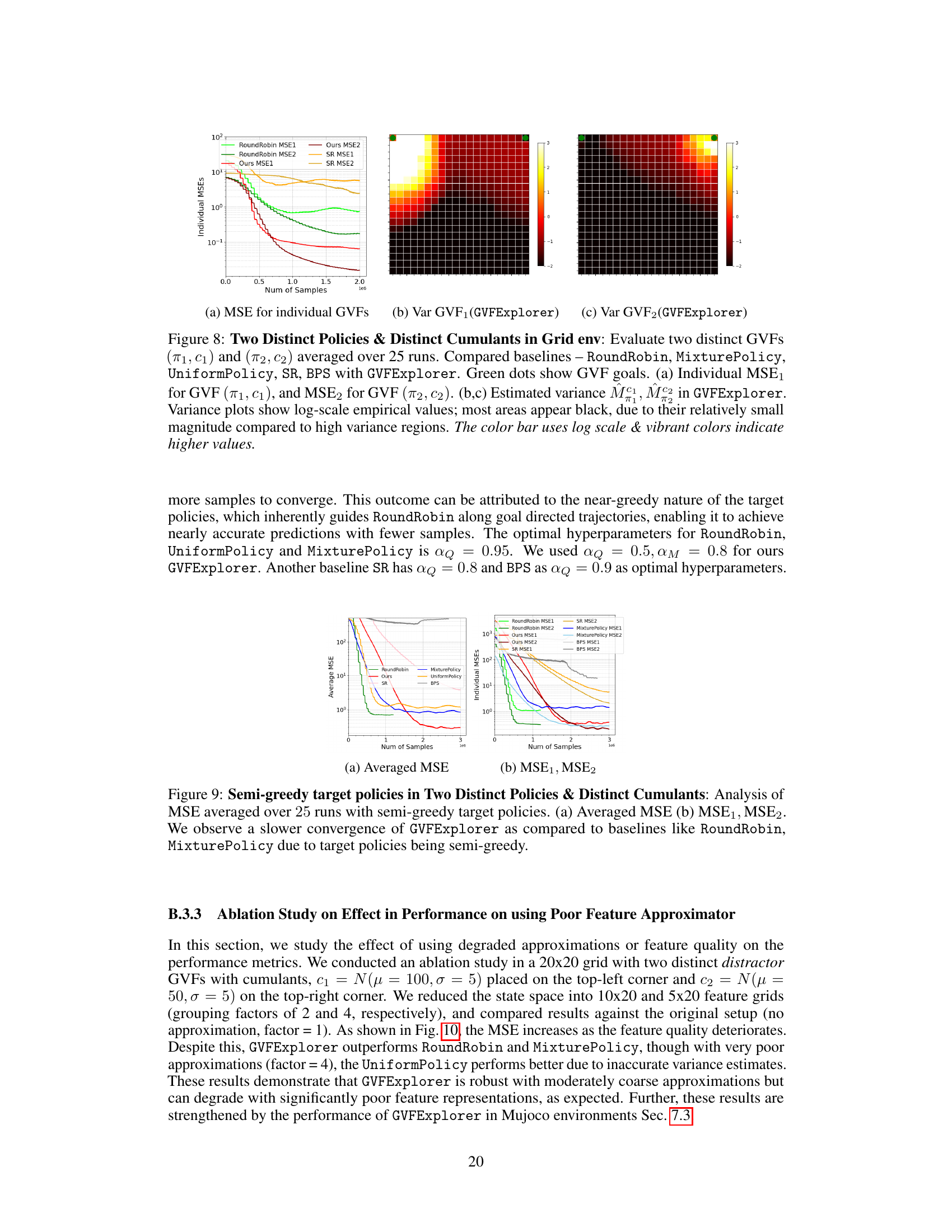
This figure compares the performance of GVFExplorer against a baseline method (RoundRobin) for estimating two General Value Functions (GVFs) with distinct target policies and distinct cumulants in a gridworld environment. The averaged Mean Squared Error (MSE) is shown, along with heatmaps visualizing the absolute error in GVF value predictions for both methods. The heatmaps reveal that GVFExplorer achieves significantly lower errors, particularly in areas where the RoundRobin baseline exhibits higher uncertainty.
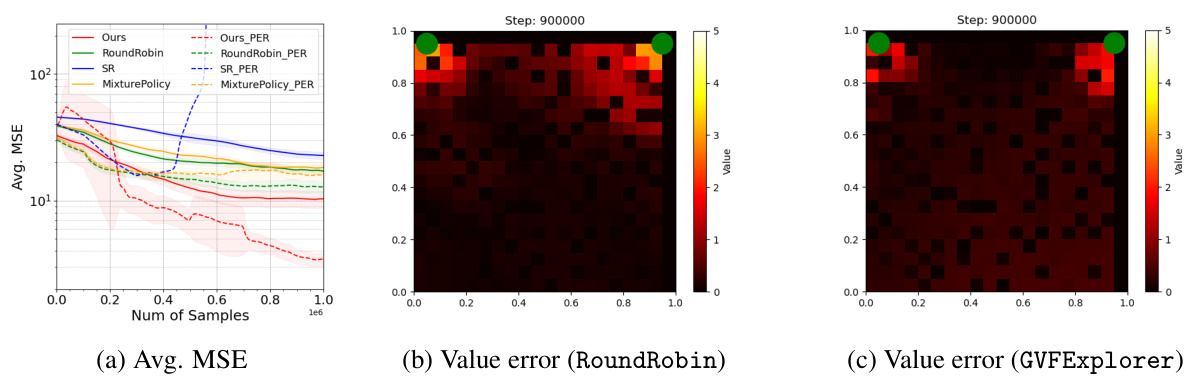
This figure compares the performance of GVFExplorer against several baselines in a continuous state environment with non-linear function approximation using both standard experience replay and prioritized experience replay (PER). The results show that GVFExplorer achieves the lowest mean squared error (MSE) in both cases, highlighting the effectiveness of the algorithm even with complex function approximation. The use of PER further improves the performance of all methods.
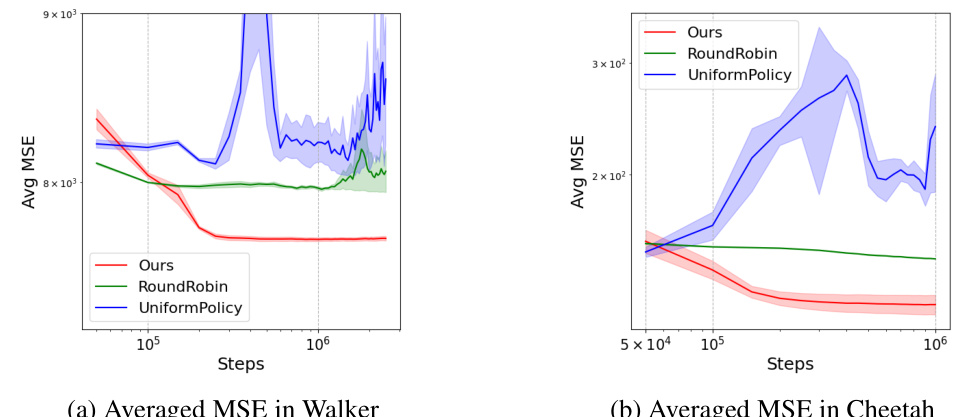
This figure compares the performance of GVFExplorer against two baselines (UniformPolicy and RoundRobin) across two MuJoCo environments (Walker and Cheetah) in terms of averaged Mean Squared Error (MSE). The results show that GVFExplorer consistently achieves lower MSE than the baselines, highlighting its effectiveness in efficiently learning multiple General Value Functions (GVFs) in complex continuous control environments.

This figure shows three different types of cumulants used in the paper’s experiments: constant, distractor, and drifter. The constant cumulant has a fixed value. The distractor cumulant is a stationary signal with a fixed mean and variance, following a normal distribution. The drifter cumulant is a non-stationary signal, modeled as a zero-mean random walk with low variance. The figure visually represents how each type of cumulant varies over time.
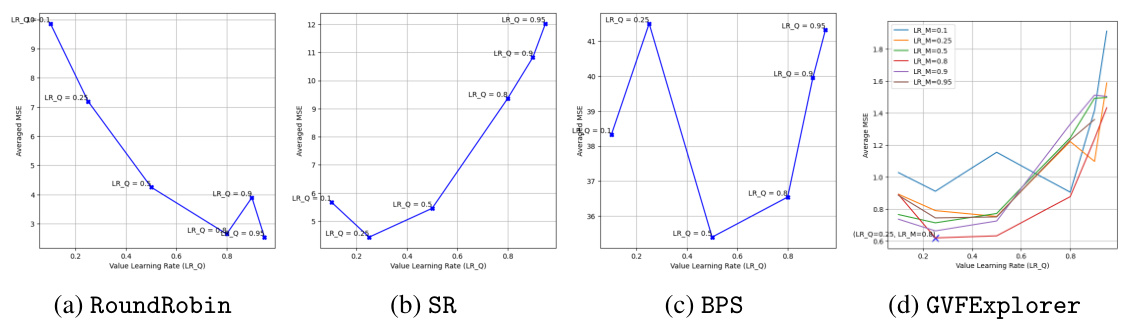
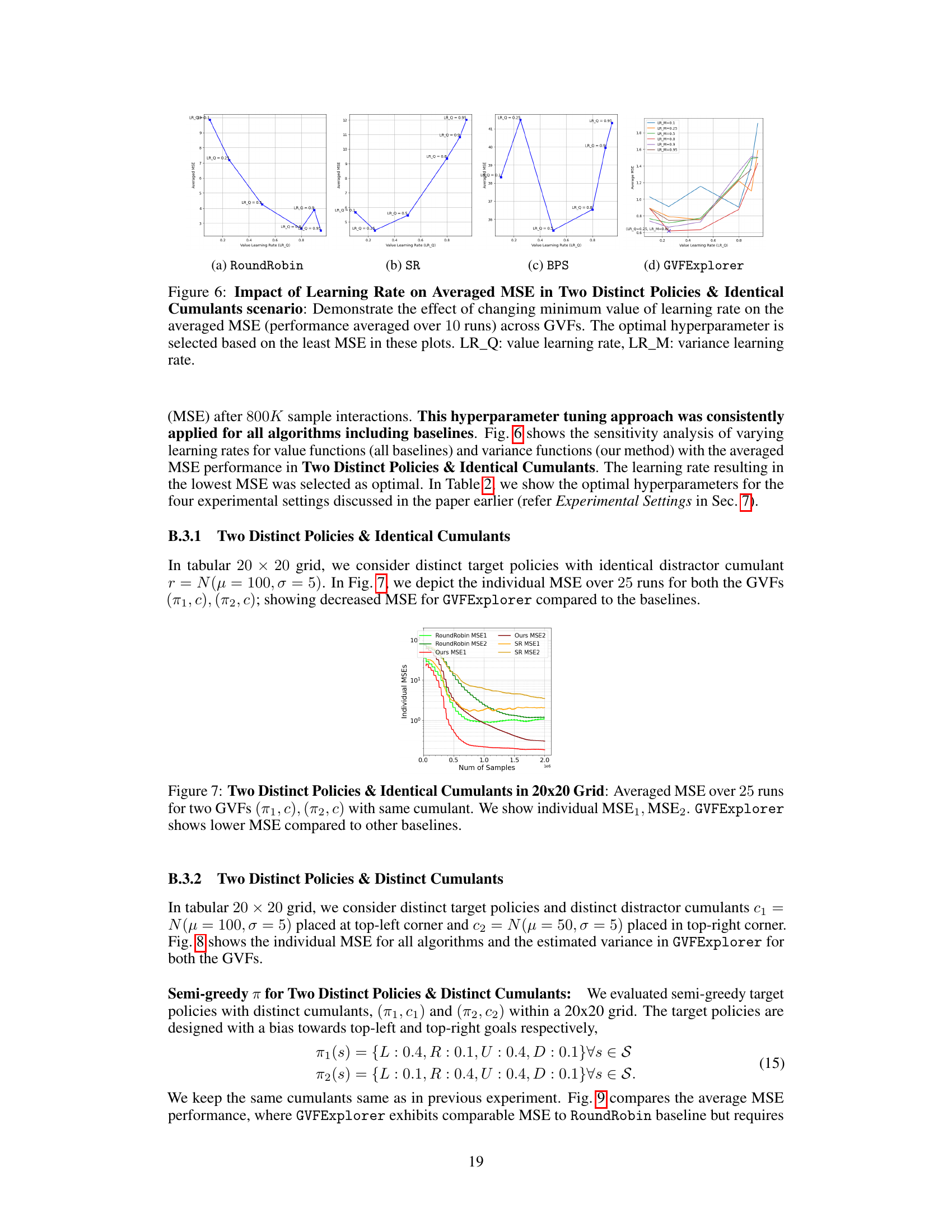
This figure shows the sensitivity analysis of varying learning rates for value functions (all baselines) and variance functions (GVFExplorer) with the averaged MSE performance in Two Distinct Policies & Identical Cumulants. The learning rate resulting in the lowest MSE was selected as optimal. For each algorithm, the averaged MSE across multiple GVFs is shown. The optimal hyperparameters for each algorithm are obtained from these plots by selecting the combination of learning rates that resulted in the lowest MSE.

This figure shows the mean squared error (MSE) for two different general value functions (GVFs) over 25 independent runs in a 20x20 gridworld environment. The two GVFs use distinct target policies but share the same cumulant (a distractor cumulant). The figure compares the performance of GVFExplorer to several baseline methods (RoundRobin, SR, etc.). The results demonstrate that GVFExplorer achieves a lower MSE than the baselines, indicating improved performance in estimating the value functions.
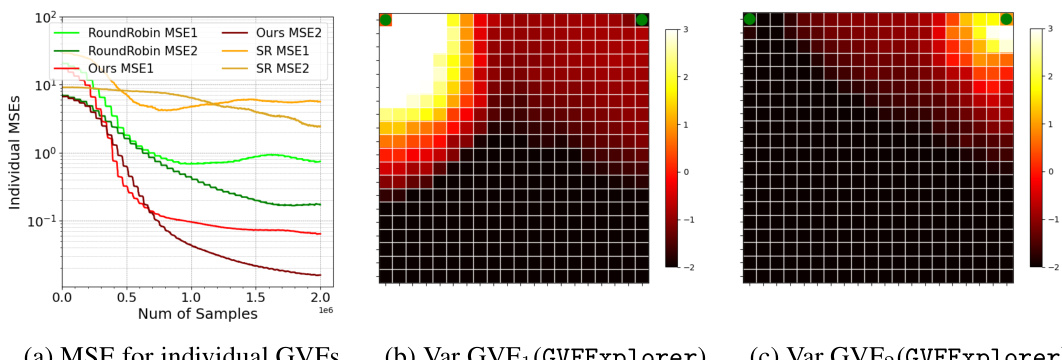
This figure shows the results of an experiment comparing GVFExplorer to several baseline methods for estimating two distinct general value functions (GVFs) in a grid environment. The GVFs have different target policies and distinct distractor cumulants. The figure shows (a) the individual mean squared error (MSE) for each GVF over 25 runs. Panels (b) and (c) show the estimated variance of the returns for each GVF, illustrating the higher variance areas that GVFExplorer prioritizes. The results demonstrate GVFExplorer’s superior performance in minimizing MSE compared to the baselines.
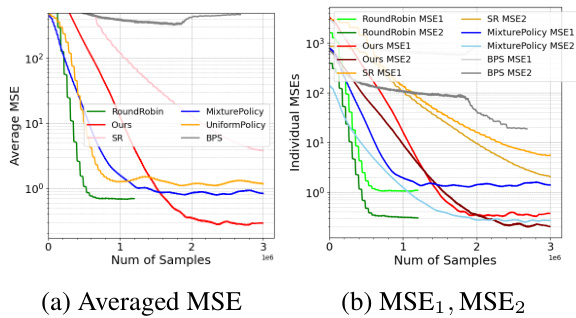
This figure compares the performance of GVFExplorer against several baseline methods in terms of Mean Squared Error (MSE) across multiple General Value Functions (GVFs). The results are shown for three different experimental settings: 1) Two distinct policies with identical cumulants, 2) Non-stationary cumulants in a FourRooms environment, and 3) a large-scale evaluation involving 40 distinct GVFs. In all three scenarios, GVFExplorer demonstrates significantly lower MSE compared to baselines, indicating its superior performance in accurately estimating multiple GVFs with improved data efficiency.

This figure shows how the performance of different algorithms changes when the resolution of the state space representation is reduced. As expected, performance degrades for all algorithms with lower resolution due to loss of information. However, GVFExplorer consistently outperforms the other methods even at lower resolutions. This highlights the algorithm’s robustness to less precise state representations.
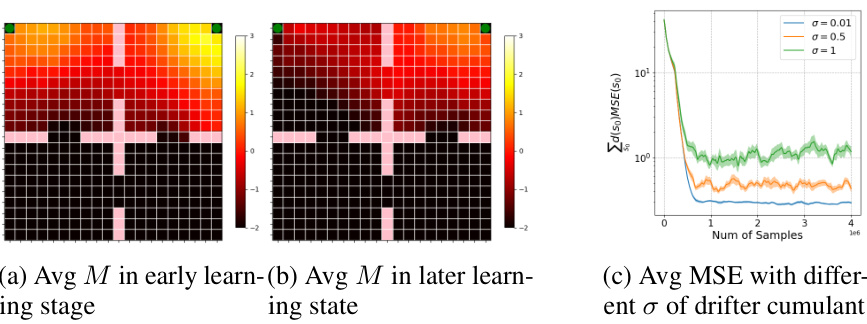
This figure demonstrates the performance of GVFExplorer in a FourRooms environment with non-stationary rewards. Panels (a) and (b) show heatmaps of the estimated variance (M) at different stages of training, illustrating how GVFExplorer adapts to track the changing reward. Panel (c) shows how the average MSE changes as the variability (σ) of the non-stationary reward is increased, revealing GVFExplorer’s robustness to this variation.
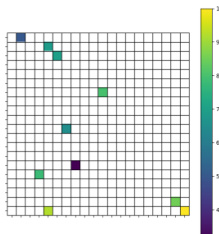
This figure shows the 10 different cumulants used in the large-scale evaluation experiment with 40 distinct GVFs. Each cumulant is assigned to a specific region (goal) in the 20x20 gridworld environment. The color intensity of each grid cell represents the empirical value of the cumulant in that region. The figure helps to visualize the distribution of cumulants across the gridworld and aids in understanding how different cumulants contribute to the overall GVF evaluation task.
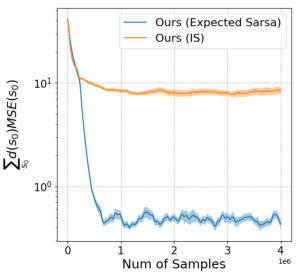
The figure compares the performance of using Importance Sampling (IS) and Expected Sarsa for updating the value function in the FourRooms environment. It shows that Expected Sarsa achieves a lower mean squared error (MSE) and converges faster than IS. This indicates that Expected Sarsa is a more effective method for off-policy learning in this environment.

This figure compares the performance of different algorithms with and without prioritized experience replay (PER) for estimating general value functions in a continuous state environment with non-linear function approximation. It shows that GVFExplorer consistently achieves lower mean squared error (MSE) than the other baselines, both with and without PER. The use of PER further improves the performance of most algorithms, especially GVFExplorer. The plots visualize the average MSE and the absolute error in GVF value estimations to provide a more detailed view of performance.

This figure compares the prediction errors of two different algorithms, RoundRobin and GVFExplorer, for estimating the values of two general value functions (GVFs) in a continuous environment. The top row displays the errors from the RoundRobin algorithm, while the bottom row shows the errors from the GVFExplorer algorithm. Each column shows a different metric: the average error across both GVFs, the error for the first GVF, and the error for the second GVF. The results indicate that GVFExplorer achieves lower errors, particularly in areas where RoundRobin has higher errors, demonstrating its effectiveness in minimizing overall error.
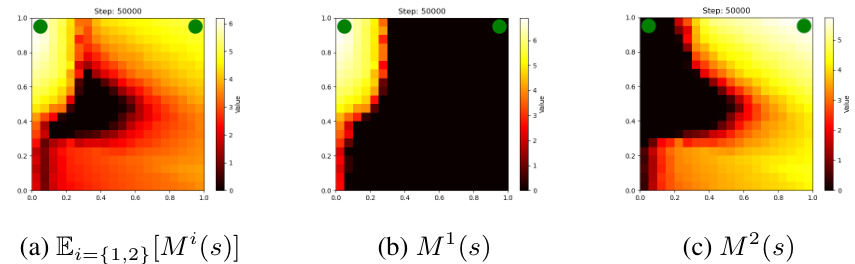
This figure shows the estimated variance of returns across states for two different GVFs (left and right goal). The color intensity reflects the magnitude of the variance, with brighter colors indicating higher variance. This visualization helps explain why GVFExplorer focuses on high-variance areas to improve the efficiency of data collection, thereby reducing the mean squared error in the GVF estimations.
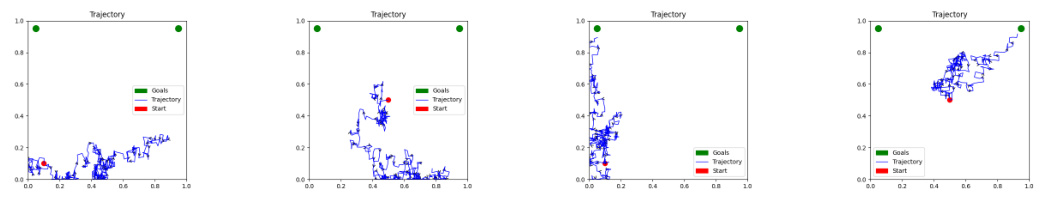
This figure compares the trajectories generated by GVFExplorer and RoundRobin in a continuous environment. GVFExplorer’s trajectories are more focused, aiming to minimize the overall variance and MSE. In contrast, RoundRobin’s trajectories follow the given target policies more directly, potentially leading to less efficient exploration and higher MSE.
More on tables
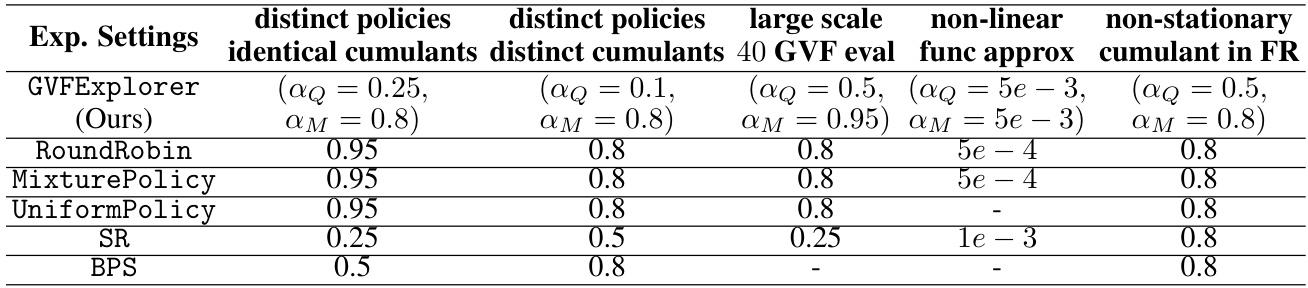
This table presents the optimal hyperparameter settings for various experimental setups used in the paper. It lists the learning rates (αQ for the Q-value network and αM for the variance network) that yielded the best performance (lowest MSE) for each experimental condition. The conditions include using identical or distinct cumulants, and the number of GVFs evaluated. The learning rates were optimized for different scenarios, demonstrating the adaptive nature of the algorithm.

This table presents the average Mean Squared Error (MSE) for two General Value Functions (GVFs) across different algorithms in a continuous environment. The algorithms are compared using both standard experience replay and prioritized experience replay, after 1 million learning steps. The table shows that GVFExplorer consistently outperforms other methods, achieving lower MSE across both replay buffer types. The percent improvement of GVFExplorer over the best-performing baseline is also provided.
Full paper#