↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Graph-based semi-supervised learning (SSL) methods, particularly Laplace learning, often struggle with low label rates and class imbalances. These limitations arise from the degeneracy of solutions near decision boundaries, exacerbated by post-hoc thresholding to obtain discrete predictions from continuous outputs. Existing solutions like mean-shift heuristics only partially mitigate these issues and may not provide exact integer solutions.
CutSSL is proposed as a novel framework that formulates SSL as a continuous nonconvex quadratic program. Unlike previous methods, CutSSL is guaranteed to produce integer solutions, eliminating the need for heuristic thresholding and addressing the degeneracy problem. It connects to Laplace learning and mean-shift heuristics, providing new insights into their performance. CutSSL demonstrates superior performance on various benchmark datasets, surpassing state-of-the-art methods, especially in low-label and imbalanced scenarios.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in semi-supervised learning and graph-based methods. It directly addresses the limitations of existing Laplace learning algorithms, offering a novel and significantly improved approach. Its scalability and performance on large datasets make it highly relevant to current research trends, opening exciting avenues for future work on handling class and label imbalances.
Visual Insights#
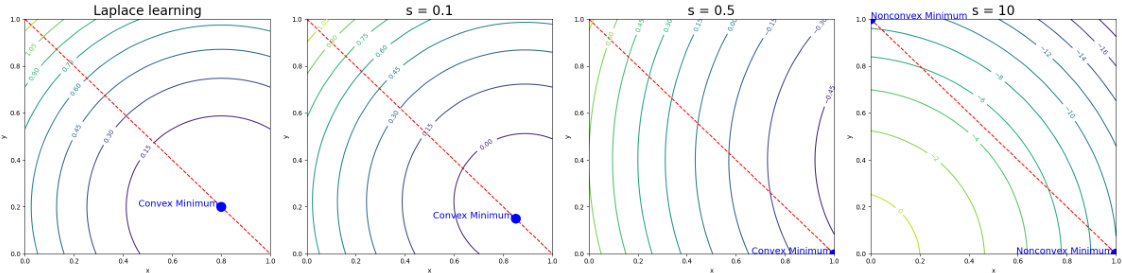
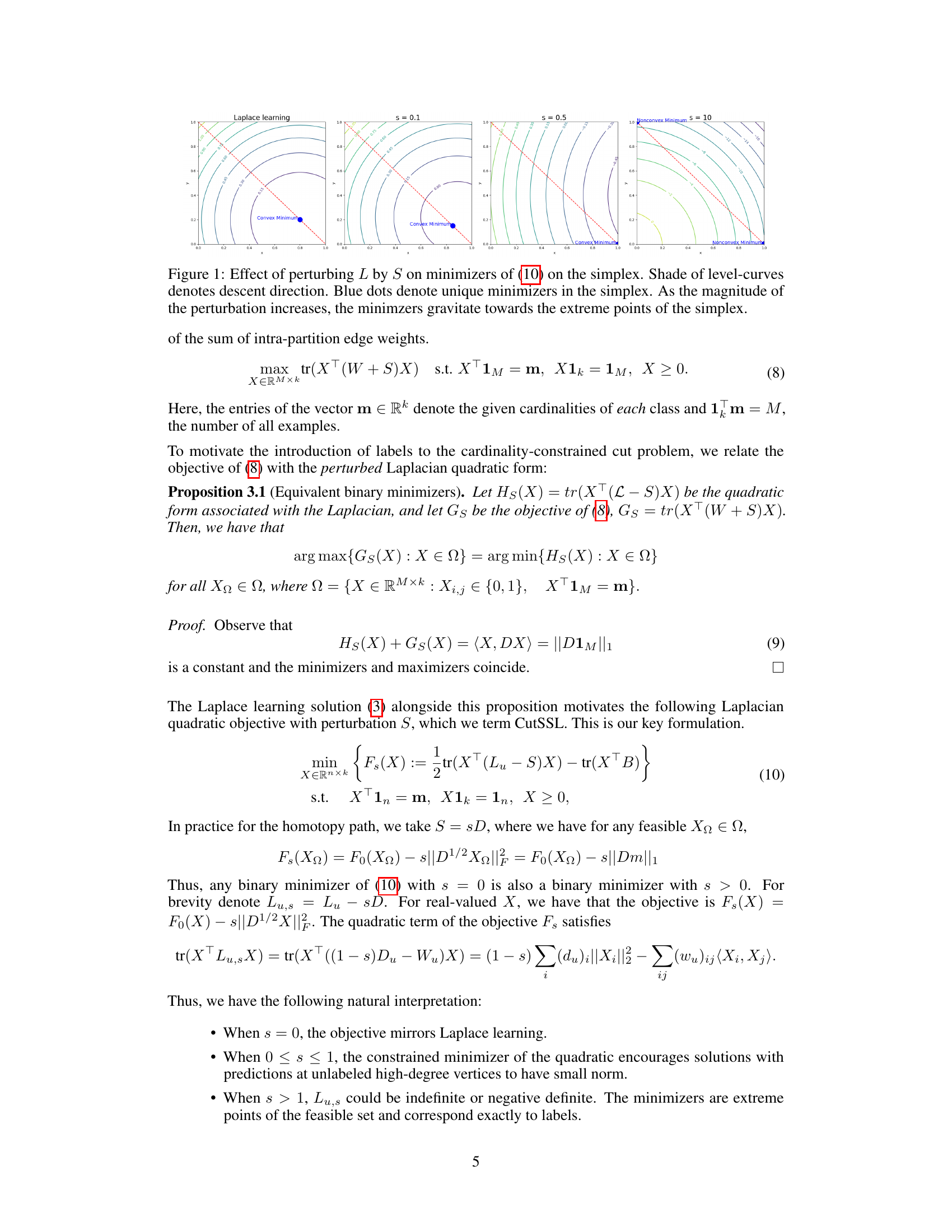
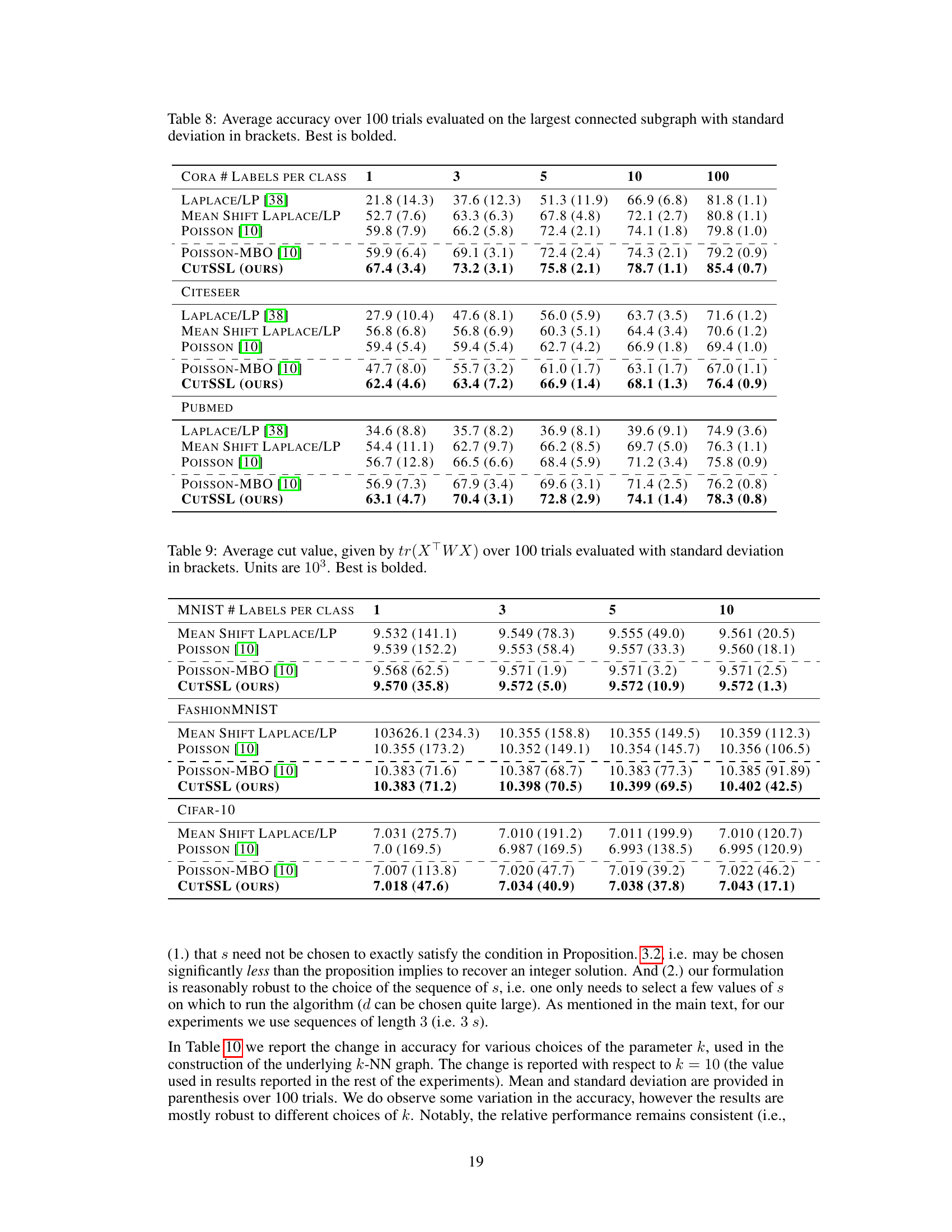
This figure shows how adding a perturbation matrix S to the graph Laplacian L affects the minimizers of the objective function in equation (10). As the value of s (scaling factor for S) increases, the initially convex objective function becomes non-convex, and the minimum shifts from the interior of the simplex (representing a non-integer solution) towards its vertices (representing integer solutions). This illustrates the core idea of the CutSSL method, where a controlled perturbation drives the optimization towards integer solutions representing smooth discrete label assignments.

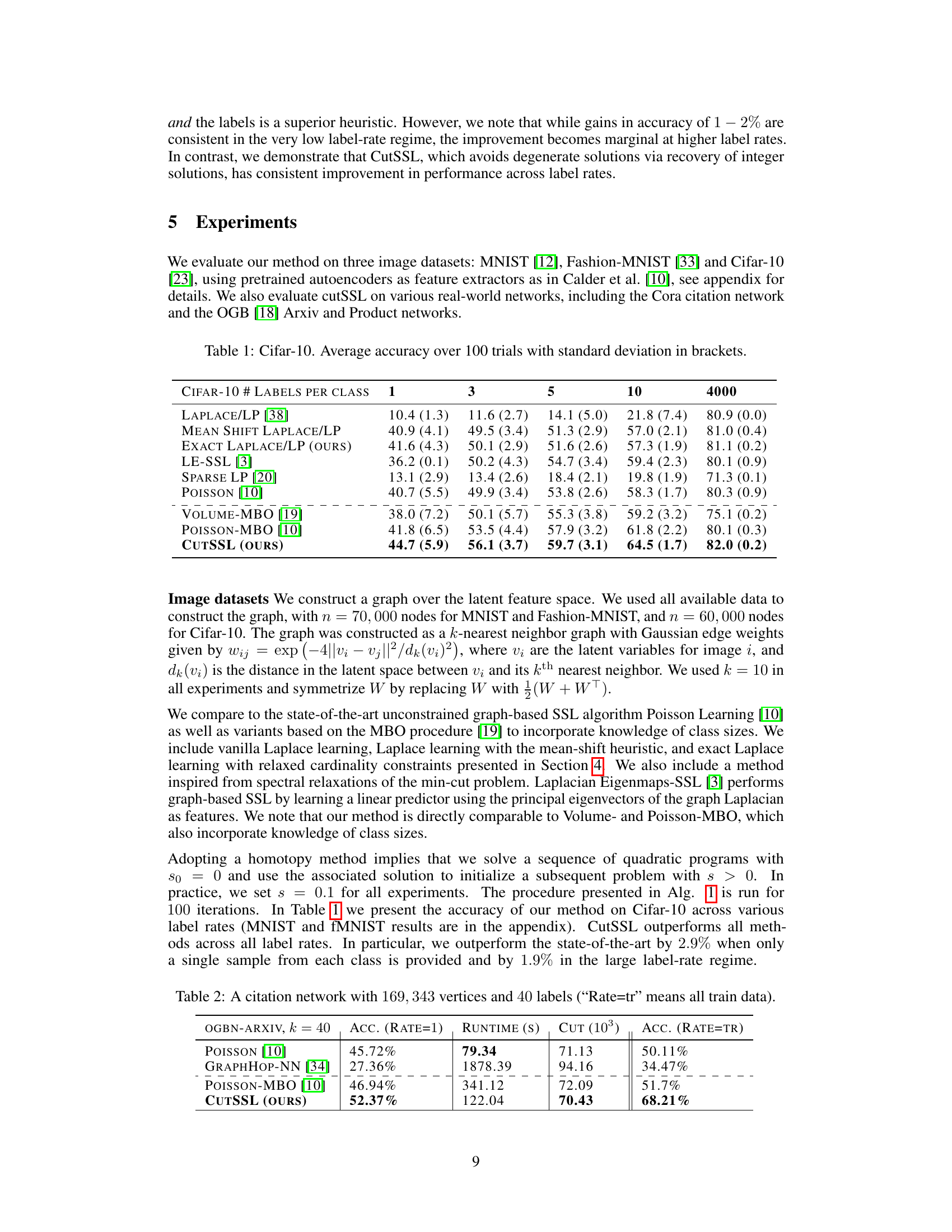
This table presents the average accuracy and standard deviation of different semi-supervised learning methods on the CIFAR-10 dataset. The results are broken down by the number of labeled examples per class (1, 3, 5, 10, and 4000). The methods compared include Laplace learning, mean-shifted Laplace learning, exact Laplace learning, LE-SSL, sparse LP, Poisson learning, Volume-MBO, Poisson-MBO, and CutSSL. The table highlights CutSSL’s superior performance, especially at low label rates.
In-depth insights#
CutSSL Framework#
The CutSSL framework, introduced for graph-based semi-supervised learning, presents a novel approach to address limitations of existing methods like Laplace learning. CutSSL tackles degeneracy issues at low label rates and in imbalanced class scenarios by formulating the problem as a continuous nonconvex quadratic program, which provably obtains integer solutions. This contrasts with relaxations used in other methods, leading to a more accurate and stable solution. The framework’s connection to the minimum-cut graph partitioning problem provides theoretical grounding, and its relation to mean-shifted Laplace learning offers insights into existing heuristics. CutSSL demonstrates significant improvements over state-of-the-art techniques in various label rate and imbalance regimes, across different graph structures, and showcases scalability to large real-world datasets. The efficiency of the ADMM-based iterative solution method is a key strength, further enhancing the framework’s practical applicability.
ADMM Algorithm#
The Alternating Direction Method of Multipliers (ADMM) algorithm, as applied in this research, is a crucial component for solving the non-convex quadratic program formulated for semi-supervised learning. ADMM’s strength lies in its ability to decompose complex problems into smaller, more manageable subproblems, making it particularly well-suited for large-scale graph-based data. The iterative nature of ADMM, involving alternating updates of primal and dual variables, ensures convergence to a solution, although theoretical guarantees often require convexity assumptions which are not satisfied in this context. The authors’ use of ADMM on a non-convex problem is notable, highlighting the practical efficacy of the approach, even if global optimality cannot be guaranteed. The choice to employ ADMM showcases a focus on scalability and numerical efficiency, critical considerations when tackling the massive datasets often involved in graph-based SSL. Further details on the convergence properties and computational complexity within the context of non-convexity would strengthen the analysis. The paper should discuss the specific parameters used in the ADMM implementation, as these settings may significantly affect the algorithm’s performance.
Mean-Shift Link#
The concept of a “Mean-Shift Link” in the context of semi-supervised learning on graphs suggests a connection between the standard Laplace learning approach and a refined heuristic that addresses its limitations. Laplace learning, while elegant in its theoretical foundation, suffers from degeneracy at low label rates, producing homogenous predictions. The mean-shift heuristic attempts to mitigate this issue by shifting the predictions to ensure that the column means of the prediction matrix are zero. This effectively counteracts the tendency toward degenerate estimates near decision boundaries, improving predictive accuracy. A “Mean-Shift Link” would analyze the precise mathematical relationship between these two methods, possibly revealing the mean-shift as an approximate solution to a modified optimization problem, perhaps one incorporating cardinality constraints to ensure discrete label assignments. This connection could provide valuable insights into the behavior of both methods and potentially lead to more robust and accurate semi-supervised learning algorithms that seamlessly integrate the benefits of Laplace learning with the corrective power of the mean shift.
Scalability & Benchmarks#
A robust research paper should dedicate a section to evaluating the scalability and performance of its proposed methods. This often involves benchmarking against existing state-of-the-art techniques using a diverse range of datasets. For algorithms operating on graphs, scalability is particularly crucial. The benchmarks should include experiments with varying graph sizes, number of nodes and edges, to assess how computational time and memory usage scale. The choice of benchmarks is critical and should reflect the target applications. Real-world datasets are ideal but can be supplemented with synthetic data that exhibit relevant characteristics. Comprehensive evaluation should consider factors such as label rate, class imbalance, and other factors impacting algorithm performance. The results should be clearly presented, ideally visually, demonstrating the trade-off between computational cost and accuracy. Finally, the authors should discuss the limitations of the benchmarking strategy and potential biases, and how future work could improve the methodology.
Future Work#
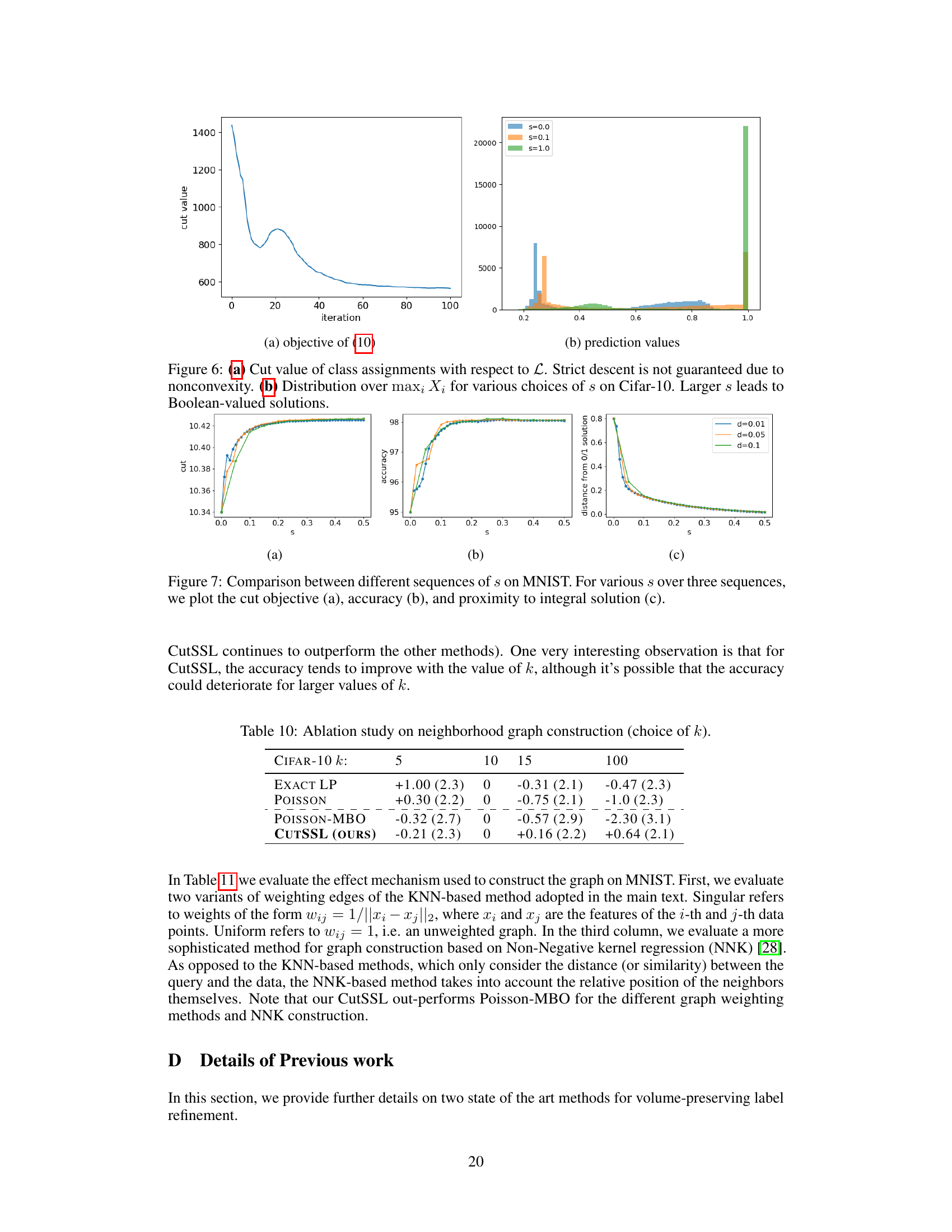
The paper’s lack of a dedicated “Future Work” section is notable. However, we can infer potential future directions based on the limitations and open questions raised. Extending CutSSL to more complex graph structures beyond k-NN graphs is crucial, as real-world networks often exhibit more intricate topologies. A deeper theoretical analysis of the algorithm’s convergence properties and conditions for exact integer solution recovery is needed. Investigating the effect of different choices of the regularization matrix S on performance is also important. Finally, applying CutSSL to a wider range of real-world problems and benchmark datasets will further validate its effectiveness and demonstrate its applicability in various domains.
More visual insights#
More on figures
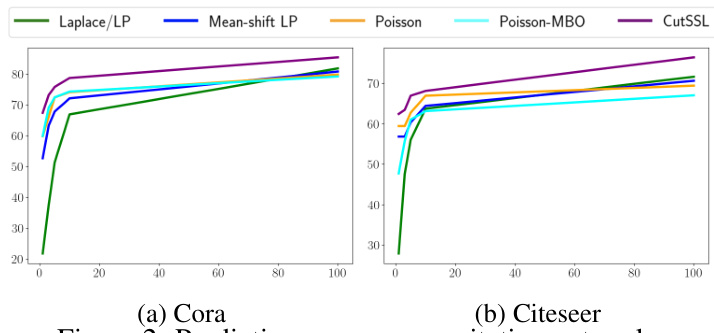
This figure shows the prediction accuracy of different semi-supervised learning methods on Cora and Citeseer citation networks, with varying label rates. It demonstrates the performance of Laplace learning, mean-shifted Laplace learning, Poisson learning, Poisson-MBO, and CutSSL across different label ratios. The graph visually represents how each method’s accuracy changes as more labels are added to the training data. It highlights the superior performance of CutSSL, especially at low label rates.
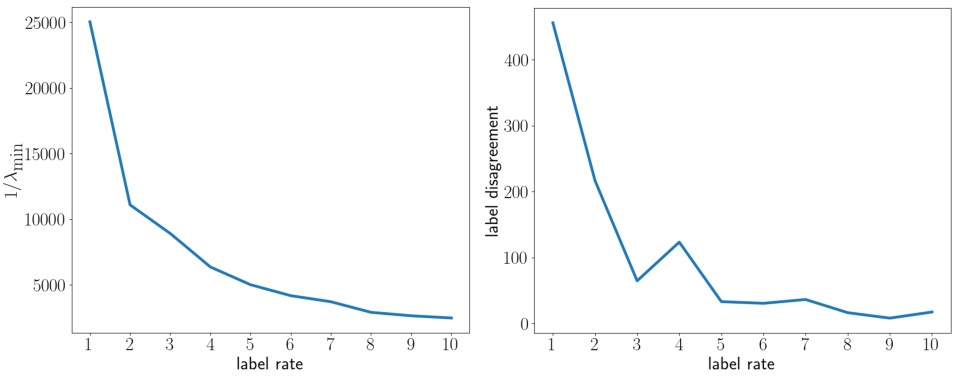
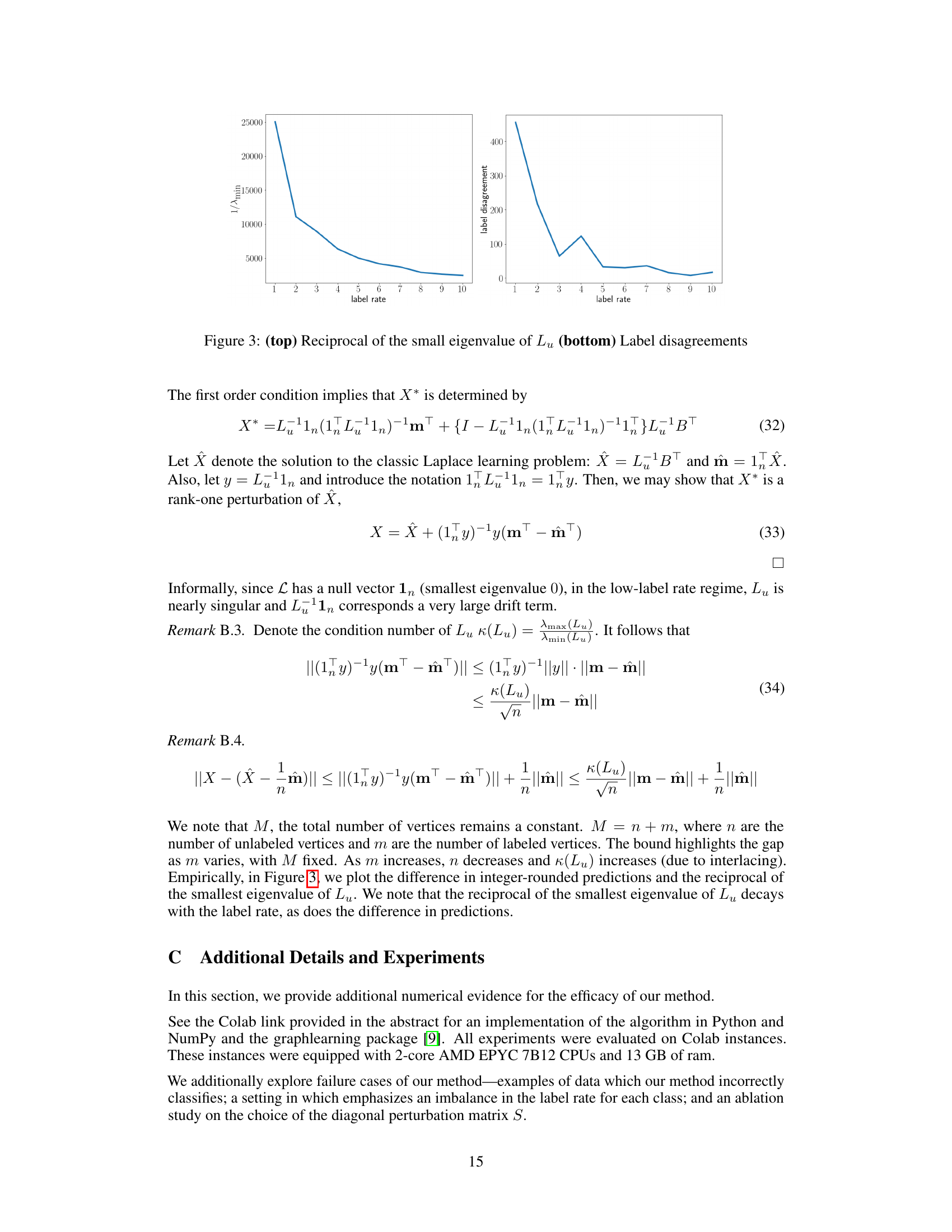
This figure shows two plots. The top plot displays the reciprocal of the smallest eigenvalue of the matrix Lu against the label rate. The bottom plot shows the number of label disagreements against the label rate. The plots illustrate how the smallest eigenvalue of Lu and the number of label disagreements change as the label rate varies. This is relevant to understanding the performance of the Laplace learning algorithm under different label rates. The figure supports the discussion on how the Laplace learning algorithm suffers from degeneracy at low label rates.

The figure shows the predicted label distributions of three different methods on the MNIST dataset with one label per class. Vanilla Laplace learning shows a highly unbalanced distribution, concentrated on one class. The mean-shift heuristic shows a much more balanced distribution across all classes. Shifting the labels alone does not produce a balanced distribution.

This figure shows examples of misclassified images from the MNIST and Fashion-MNIST datasets. These examples are specifically chosen from images located on the boundary between different partitions created by the CutSSL algorithm. The images in (a) are handwritten digits, and the images in (b) are images of clothing items. The misclassifications likely occur because these images are ambiguous or lie on the decision boundary between classes, making them difficult for the algorithm to classify accurately.
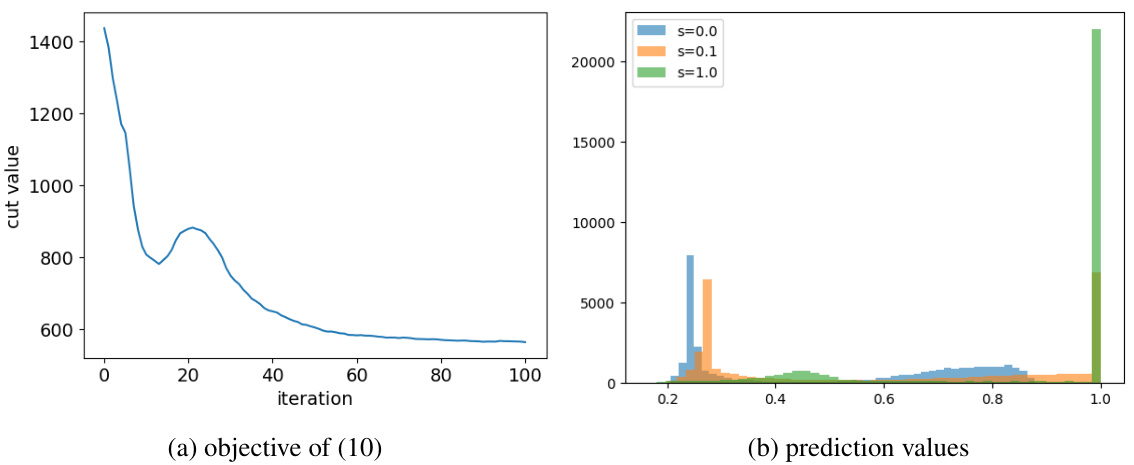
This figure visualizes how adding a perturbation matrix S to the Laplacian matrix L affects the minimizers of the objective function (10) over the probability simplex. As the magnitude of S (controlled by the scalar parameter ’s’) increases, the initially unique minimizer moves towards the vertices (corners) of the simplex, representing the binary solutions that are desirable for the graph partitioning problem. The level curves illustrate the change in the objective function’s value, and the color shading indicates the direction of descent.
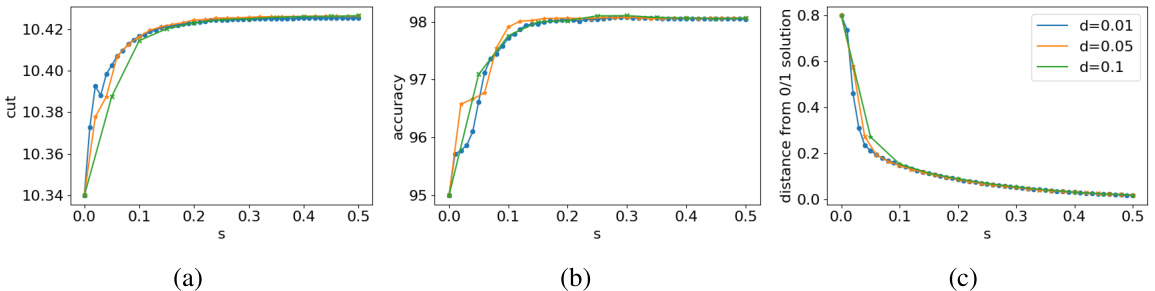
This figure shows how adding a perturbation matrix S to the Laplacian L affects the minimizers of the objective function (10) defined on the simplex. As the magnitude of S increases (controlled by parameter s), the minimizers move from the interior of the simplex to its vertices (extreme points). This illustrates the effect of the perturbation in guiding solutions towards binary values.
More on tables

This table shows the average accuracy and standard deviation of different semi-supervised learning methods on the CIFAR-10 dataset. The accuracy is shown for different numbers of labeled examples per class (1, 3, 5, 10, and 4000). The methods compared include Laplace learning, mean-shifted Laplace learning, various improvements on Laplace learning from other papers, and the CutSSL method proposed in this paper. The results demonstrate the performance of CutSSL compared to other state-of-the-art methods across different label rates.

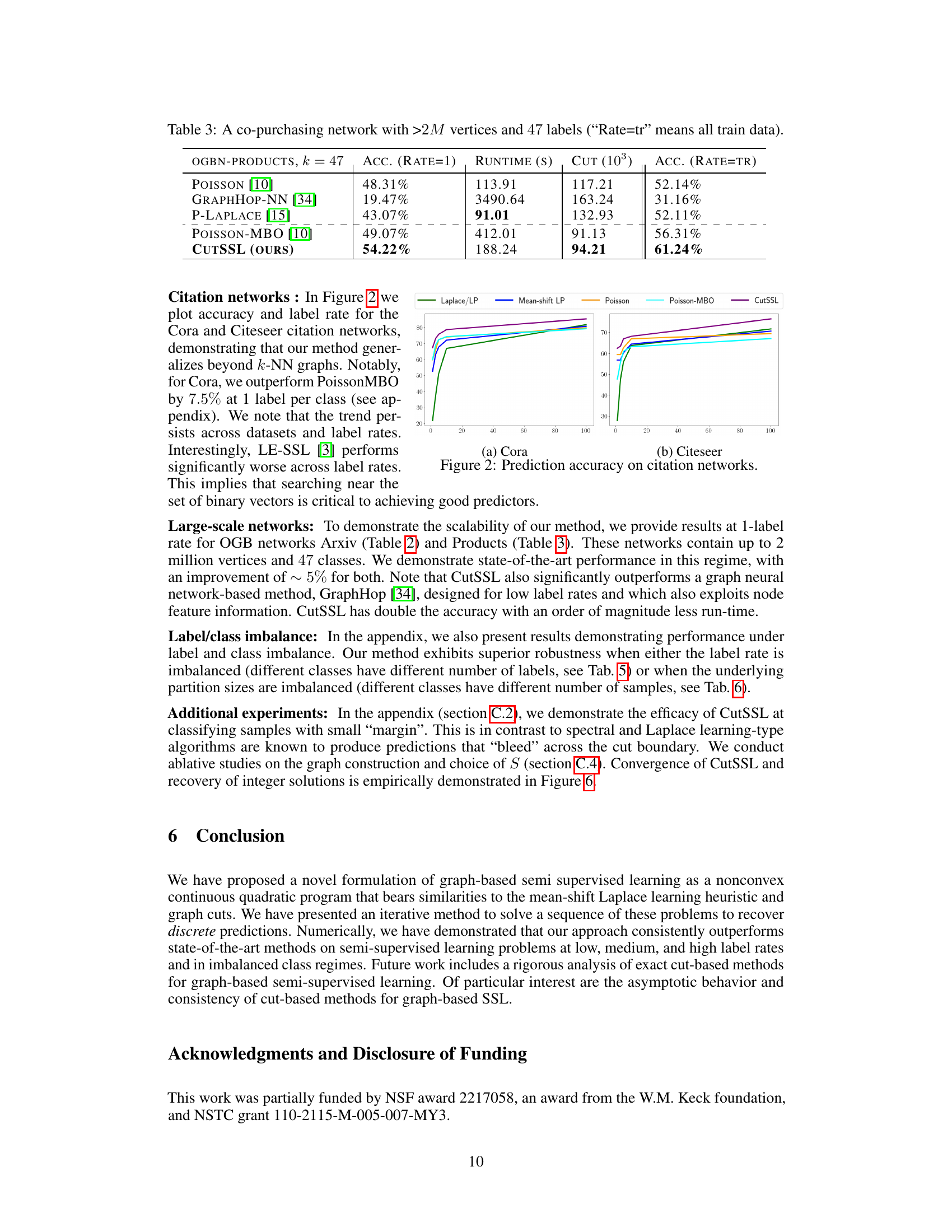
This table presents the results of the CutSSL algorithm and other baseline methods on the OGB-PRODUCTS dataset, a large-scale co-purchasing network with over 2 million vertices and 47 labels. The table shows the accuracy achieved at a label rate of 1 and at the full training rate, along with the runtime and the size of the minimum cut obtained. CutSSL significantly outperforms other methods, demonstrating its scalability and effectiveness on large, real-world datasets.

This table presents the average accuracy and standard deviation (in brackets) over 100 trials for different semi-supervised learning methods on the CIFAR-10 dataset. The results are broken down by the number of labels per class (1, 3, 5, 10, and 4000). It compares the performance of CutSSL against several baseline methods, including Laplace learning, mean-shifted Laplace learning, Poisson learning, and volume-constrained MBO methods. This allows for a direct comparison of CutSSL’s performance against state-of-the-art approaches under varying label conditions.
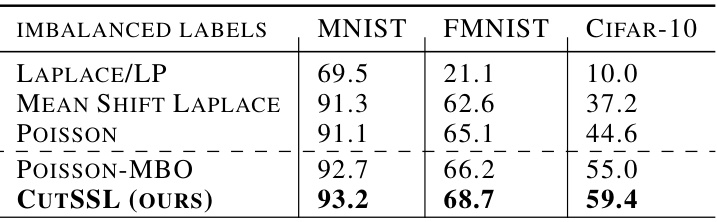
This table presents the average accuracy results for imbalanced label regimes on MNIST, FMNIST, and CIFAR-10 datasets. The imbalance is created by assigning 1 label to odd-numbered classes and 5 labels to even-numbered classes. The table compares the performance of different semi-supervised learning methods, including Laplace Learning, Mean Shift Laplace, Poisson, Poisson-MBO, and CutSSL. The results demonstrate the performance of each method under data imbalance.
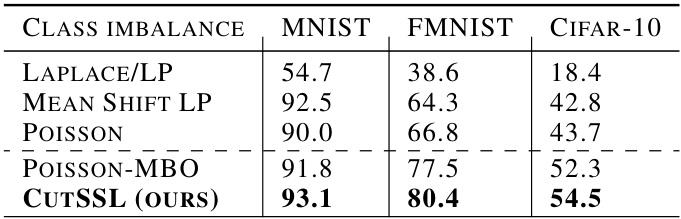
This table shows the performance of different semi-supervised learning methods on imbalanced datasets. The datasets (MNIST, Fashion-MNIST, CIFAR-10) have been modified so that even-numbered classes contain 10 times more samples than odd-numbered classes, and each odd-numbered class has only one labeled sample. The results demonstrate CutSSL’s robustness to class imbalance compared to other methods.

This table compares the accuracy of different methods (Exact Laplace/LP, Poisson, and CutSSL) on subsets of samples from the CIFAR-10 dataset, focusing on samples with the smallest margin (i.e., those closest to the decision boundary). The margin threshold is used to select samples. The results show that CutSSL has significantly higher accuracy for these hard-to-classify samples.

This table presents the average accuracy and standard deviation over 100 trials for different semi-supervised learning methods on the CIFAR-10 dataset. The methods are compared across varying numbers of labeled examples per class (1, 3, 5, 10, and 4000). The results show the performance of CutSSL in comparison to other state-of-the-art methods.

This table presents the average accuracy and standard deviation for different semi-supervised learning methods on the CIFAR-10 dataset. The accuracy is calculated over 100 trials and broken down by the number of labels per class (1, 3, 5, 10, and 4000). The methods compared include Laplace learning, mean-shifted Laplace learning, Exact Laplace learning, LE-SSL, Sparse LP, Poisson Learning, Volume-MBO, Poisson-MBO, and CutSSL. The table highlights the performance of CutSSL compared to state-of-the-art methods, particularly at low label rates.
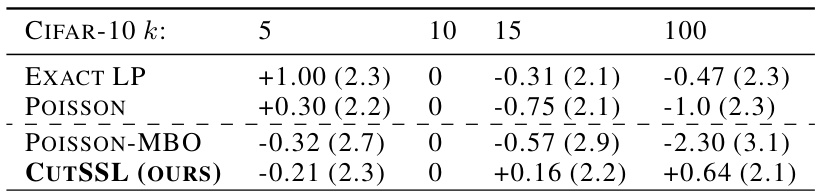
This table presents the average accuracy and standard deviation over 100 trials for different semi-supervised learning methods on the CIFAR-10 dataset. The results are broken down by the number of labels per class (1, 3, 5, 10, and 4000). The table compares the performance of CutSSL with other state-of-the-art methods, including Laplace learning, mean-shifted Laplace learning, LE-SSL, Sparse LP, Poisson learning, Volume-MBO, and Poisson-MBO.

This table presents the average accuracy and standard deviation of different semi-supervised learning methods on the CIFAR-10 dataset. The results are shown for various numbers of labeled examples per class (1, 3, 5, 10, and 4000). The methods compared include Laplace learning, mean-shifted Laplace learning, exact Laplace learning, LE-SSL, Sparse LP, Poisson learning, Volume-MBO, Poisson-MBO, and CutSSL. The table highlights the performance of CutSSL, demonstrating its superior accuracy compared to existing state-of-the-art methods, especially at lower label rates.
Full paper#