Surge Phenomenon in Optimal Learning Rate and Batch Size Scaling

↗ arXiv ↗ Hugging Face ↗ Hugging Face ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working with Adam-style optimizers because it reveals a previously unknown surge phenomenon in optimal learning rates as batch size increases. It provides a new scaling law, enabling more efficient hyperparameter tuning and faster model training. This has significant implications for improving the scalability and performance of large-scale deep learning applications.

Visual Insights

#

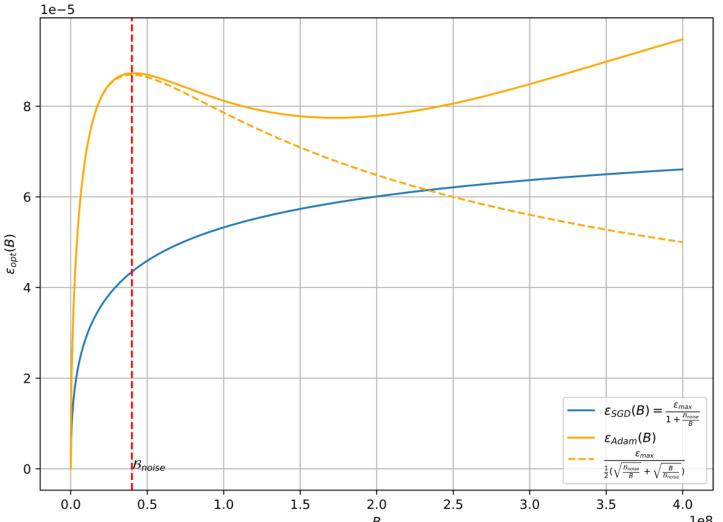
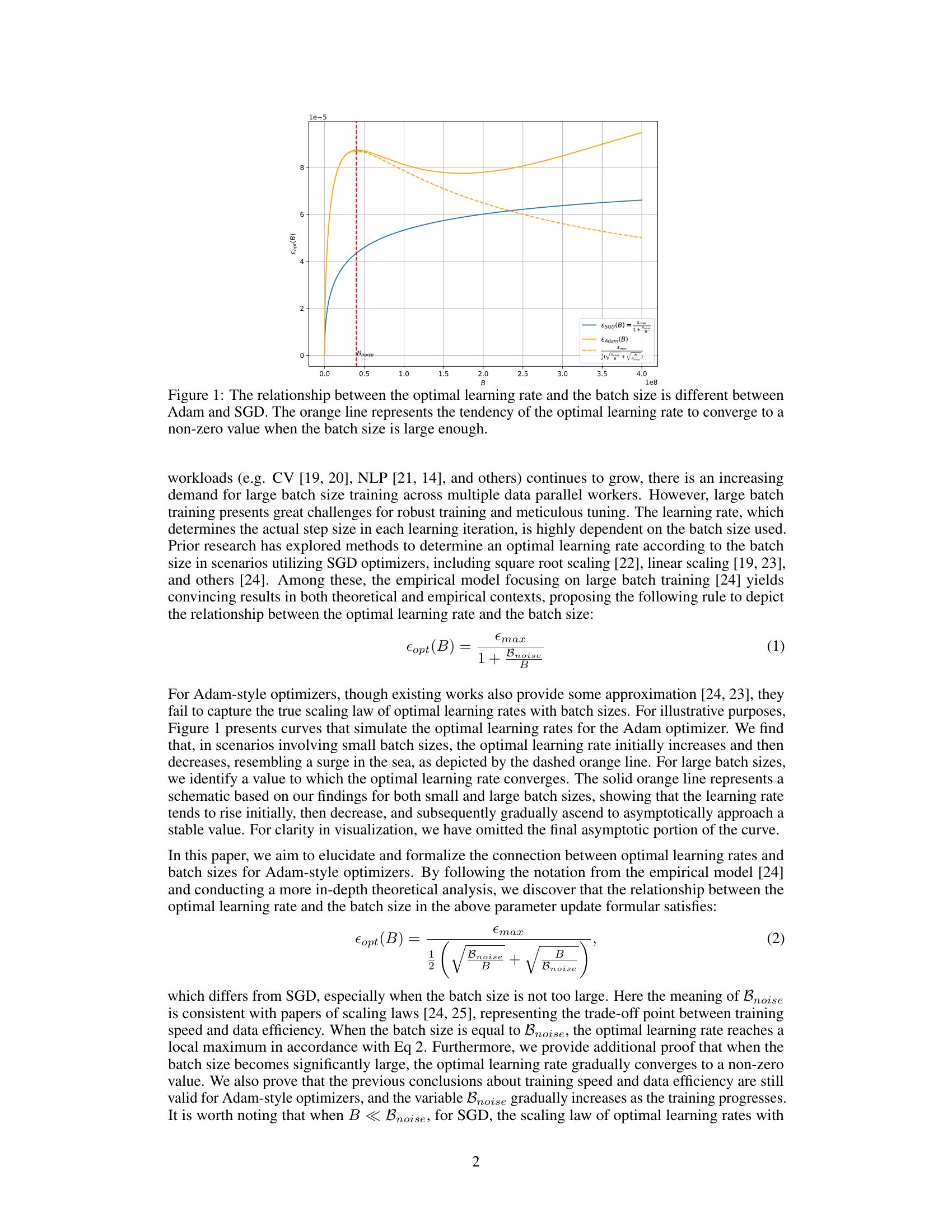
🔼 This figure illustrates the contrasting relationships between optimal learning rate and batch size for Adam-style and SGD-style optimizers. The SGD curve shows a linear increase in optimal learning rate with batch size. Conversely, the Adam curve demonstrates a surge, initially increasing, then decreasing, and finally leveling off at a non-zero value as the batch size grows large enough. This highlights a key difference in how these optimizer types respond to scaling.

read the caption

Figure 1: The relationship between the optimal learning rate and the batch size is different between Adam and SGD. The orange line represents the tendency of the optimal learning rate to converge to a non-zero value when the batch size is large enough.

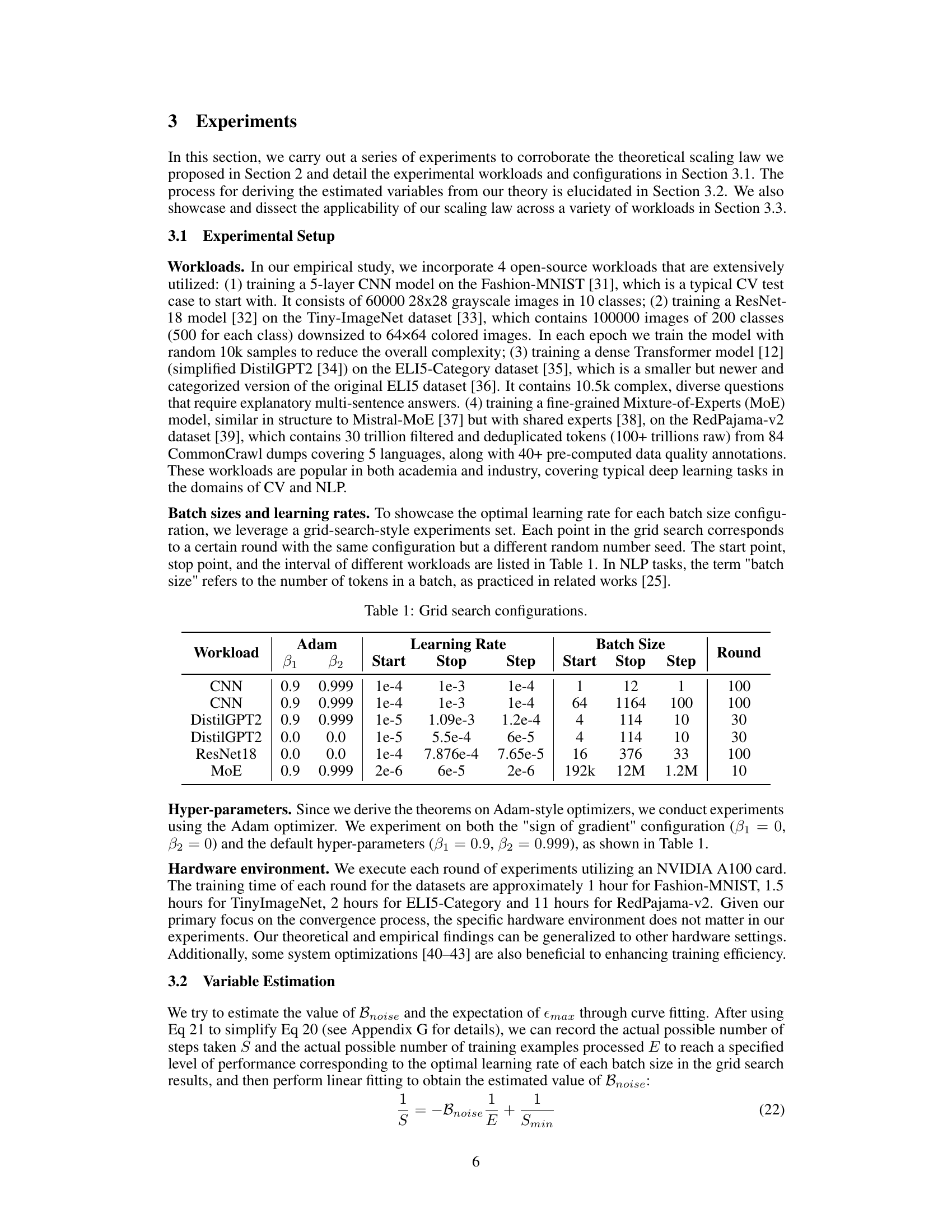
🔼 This table details the configurations used in the grid search experiments for different workloads (CNN, DistilGPT2, ResNet18, MoE). For each workload, it lists the Adam optimizer hyperparameters (β1 and β2), the range and step size for the learning rate, and the range and step size for the batch size. Finally, the number of rounds for each experiment is provided.

read the caption

Table 1: Grid search configurations.

In-depth insights

#

Adam’s Surge

#

The concept of “Adam’s Surge” refers to a phenomenon observed in the Adam optimizer, where the optimal learning rate initially increases with batch size, then decreases after reaching a peak, before eventually plateauing. This behavior contrasts sharply with SGD optimizers, which typically show a linear or square root relationship between optimal learning rate and batch size. This surge is theoretically explained by analyzing the impact of batch size on the gradient’s sign in Adam-style updates. The peak of the surge, represented by the variable Bnoise, is a critical point reflecting the trade-off between training speed and data efficiency. As training progresses, Bnoise increases, shifting the surge peak towards larger batch sizes. Understanding Adam’s Surge is vital for effective hyperparameter tuning in deep learning, particularly when employing large batch sizes. The findings highlight the need to move beyond simple scaling rules and consider the unique dynamics of Adam-style optimizers.

Batch-Size Scaling

#

Batch size scaling is a crucial aspect of deep learning optimization, impacting both training speed and model performance. Larger batch sizes generally lead to faster training by utilizing more data per update, but this can come at the cost of reduced generalization ability. The optimal learning rate also changes with batch size; naive scaling is insufficient. This paper investigates the complex relationship between batch size and learning rate, particularly for Adam-style optimizers. It introduces a theoretical analysis showing that, unlike SGD, the optimal learning rate for Adam-style optimizers exhibits a non-monotonic relationship with batch size; initially rising, then falling before stabilizing, forming a ‘surge’ phenomenon. The paper empirically validates this surge effect, demonstrating its presence across various datasets and model architectures. This challenges previous work that assumed a simpler, monotonic scaling law. The findings offer critical insights for hyperparameter tuning in Adam-based training, particularly in large-scale settings.

Theoretical Underpinnings

#

The theoretical underpinnings section of this research paper would ideally delve into the mathematical and statistical framework supporting the empirical findings. It should rigorously establish the relationship between optimal learning rates and batch sizes for Adam-style optimizers. A key element would be the derivation of the scaling law, explaining the initial increase and subsequent decrease in optimal learning rate as batch size increases. The analysis should justify the approximation used to model Adam-style optimizers, likely involving a simplification of the update rule and assumptions about the gradient distribution (e.g., Gaussian). The derivation should clearly articulate the assumptions made and their limitations, including considerations of the Hessian matrix for second-order analysis. Furthermore, the theoretical results should precisely connect to the empirical observations, providing a clear explanation for the observed surge phenomenon and subsequent asymptotic convergence. This section is crucial for establishing the validity and generalizability of the study’s findings beyond the specific experiments conducted.

Empirical Validation

#

An ‘Empirical Validation’ section in a research paper would rigorously test the study’s hypotheses. This would involve designing experiments with appropriate controls, selecting relevant datasets, and employing suitable statistical methods. Detailed descriptions of the experimental setup, including datasets, parameters, and metrics, are essential for reproducibility. The results section should clearly present the findings, often visually through graphs or tables, accompanied by a discussion of their statistical significance. A strong validation section would not only confirm or refute hypotheses, but also explore any unexpected findings and discuss potential limitations of the methodology. Finally, the results should be contextualized within the broader scientific literature to highlight the study’s contributions and implications. The overall quality of the empirical validation is crucial for assessing the reliability and significance of the research claims.

Future Directions

#

Future research could explore extending the theoretical analysis to other Adam-style optimizers and investigating the impact of different hyperparameter configurations on the surge phenomenon. A deeper exploration of the relationship between gradient noise and optimal learning rates is crucial, potentially involving higher-order approximations of the loss function to capture the complex dynamics. Investigating adaptive learning rate and batch size scheduling algorithms that leverage the discovered scaling laws would be beneficial for practical applications. Furthermore, research into the interplay of the surge phenomenon with other factors influencing model convergence, such as weight decay and gradient clipping, would offer valuable insights. Finally, applying the findings to various architectures beyond those studied, and evaluating performance across a broader range of deep learning tasks, would contribute to a more robust understanding of optimal learning rate and batch size scaling.

More visual insights

#

More on figures

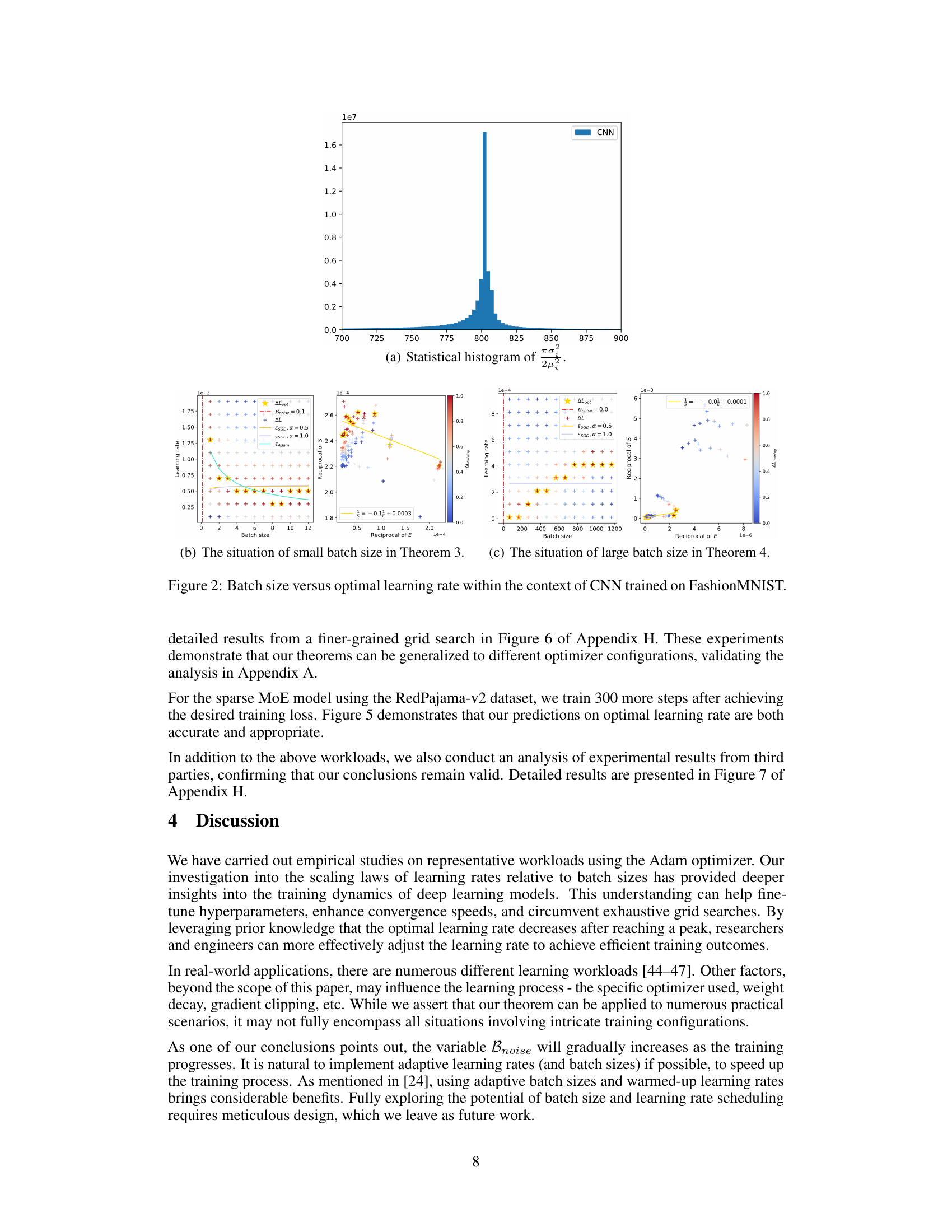
🔼 This figure shows the relationship between batch size and optimal learning rate for a Convolutional Neural Network (CNN) trained on the Fashion-MNIST dataset. It includes three subfigures: (a) a statistical histogram showing the distribution of the term (πσ²/2μ²)²; (b) illustrating the relationship for small batch sizes, aligning with Theorem 3 from the paper; and (c) illustrating the relationship for larger batch sizes, according to Theorem 4. The plots visually represent how the optimal learning rate changes as batch size increases, demonstrating the ‘surge’ phenomenon described in the paper. The plots also include curves generated using existing SGD scaling laws for comparison, illustrating the difference in scaling behavior between Adam-style and SGD optimizers.

read the caption

Figure 2: Batch size versus optimal learning rate within the context of CNN trained on FashionMNIST.

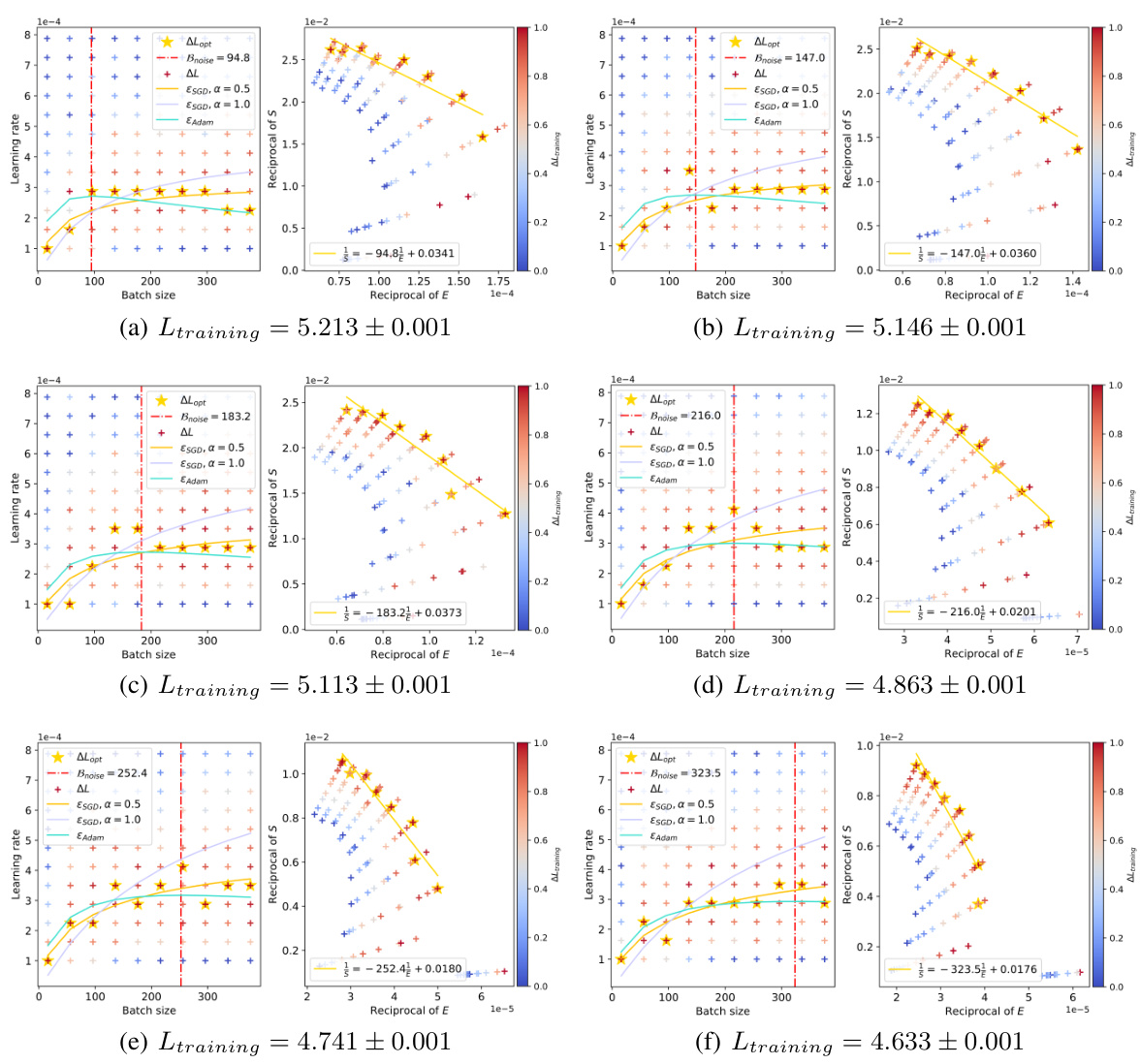
🔼 This figure shows the relationship between batch size and optimal learning rate for the ResNet-18 model trained on the TinyImageNet dataset. The figure is a grid plot showing multiple trials for each batch size, showing a surge (increase and then decrease) in optimal learning rate as batch size increases. The peak of the optimal learning rate moves to the right (larger batch sizes) as the training loss decreases. A red dashed line shows the model fit which the authors propose in the paper. This illustrates the non-linear relationship between batch size and optimal learning rate in Adam-style optimizers.

read the caption

Figure 3: The relationship between batch sizes and optimal learning rates within the context of ResNet-18 trained on TinyImageNet. The red dashed line accurately predicts the peak value, and as the training loss decreases, the peak value gradually shifts to the right.

🔼 This figure visualizes the relationship between batch size and optimal learning rate for the DistilGPT2 model trained on the ELI5-Category dataset. It shows two scenarios: one with Adam optimizer’s hyperparameters set to β₁ = 0.0, β₂ = 0.0 (sign of gradient), and another with β₁ = 0.9, β₂ = 0.999 (default Adam). The plots illustrate how the optimal learning rate initially increases and then decreases as the batch size increases, resembling a surge. The figure also shows the estimated values of Bnoise and Emax for each configuration, and compares the results with fitted curves from previous research for SGD optimizers.

read the caption

Figure 4: The relationship between batch sizes and optimal learning rates within the context of DistilGPT2 trained on Eli5Category.

🔼 This figure visualizes the relationship between batch size and optimal learning rate for a Convolutional Neural Network (CNN) trained on the Fashion-MNIST dataset. The left subplot shows the results of a grid search, plotting various learning rates against different batch sizes, color-coded by the final training loss achieved. The right subplot presents fitted curves based on theoretical analysis, comparing the proposed scaling law (orange line) with linear and square root scaling laws commonly used for SGD-type optimizers. This comparison highlights the difference between Adam-style optimizers and SGD-style optimizers in terms of how optimal learning rate scales with batch size.

read the caption

Figure 2: Batch size versus optimal learning rate within the context of CNN trained on FashionMNIST.

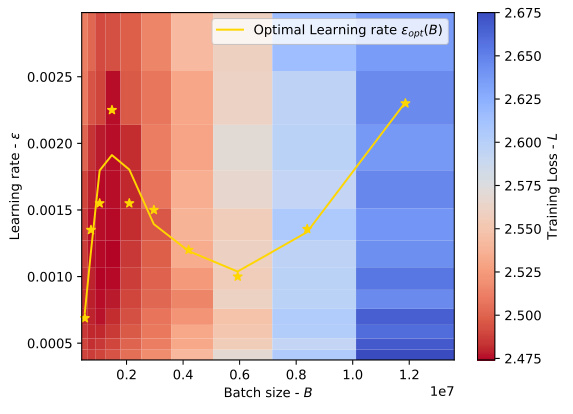
🔼 This figure presents a more detailed grid search focusing on the relationship between batch size and optimal learning rate for the DistilGPT2 model trained on the ELI5-Category dataset, specifically expanding upon the results shown in Figure 4(b). The heatmap shows the training loss (color coded) across various batch size and learning rate combinations, while the yellow line highlights the optimal learning rate for each batch size. The finer granularity of this grid search provides a more precise visualization of the optimal learning rate’s behavior.

read the caption

Figure 6: Finer-grained grid search results for the experiments shown in Figure 4(b).

🔼 This figure visualizes the relationship between batch size and optimal learning rate for a Convolutional Neural Network (CNN) trained on the Fashion-MNIST dataset. The left panel shows a heatmap illustrating the training loss achieved with different combinations of batch size and learning rate. The right panel displays the optimal learning rate (y-axis) plotted against the batch size (x-axis). The orange line represents the theoretical prediction of the optimal learning rate based on the authors’ proposed model, showcasing how the optimal learning rate initially increases, then decreases, and finally plateaus as the batch size grows larger. This behavior contradicts previous findings that learning rate increases monotonically with batch size. The figure demonstrates the ‘surge phenomenon’ described in the paper, where the optimal learning rate peaks at a specific batch size before decreasing, a phenomenon not captured by previous models.

read the caption

Figure 2: Batch size versus optimal learning rate within the context of CNN trained on FashionMNIST.

🔼 This figure shows the relationship between batch size and optimal learning rate for a Convolutional Neural Network (CNN) trained on the Fashion-MNIST dataset. The left panel displays the results of a grid search showing training loss as a heatmap with different batch sizes and learning rates. The right panel displays a curve showing the optimal learning rate across various batch sizes, along with theoretical curves for comparison. This illustrates the ‘surge phenomenon’ described in the paper where the optimal learning rate initially rises, then falls before eventually plateauing.

read the caption

Figure 2: Batch size versus optimal learning rate within the context of CNN trained on FashionMNIST.

🔼 This figure shows the relationship between batch size and optimal learning rate for a Convolutional Neural Network (CNN) trained on the Fashion-MNIST dataset. The left subplot displays the results of a grid search, showing the optimal learning rates for various batch sizes. The right subplot displays curves fitting to the data from the left subplot which depicts the theoretical relationship between optimal learning rate and batch size according to Theorem 3 and Theorem 4 from the paper. The figure demonstrates that the optimal learning rate initially increases, then decreases (a surge), and eventually plateaus as the batch size increases, as predicted by the theoretical analysis.

read the caption

Figure 2: Batch size versus optimal learning rate within the context of CNN trained on FashionMNIST.

Full paper

#