↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Molecular learning, crucial for drug discovery, faces challenges due to the high cost of human annotation for molecular data. Active learning (AL) offers a solution by automatically querying labels for the most informative samples. Existing AL methods struggle with 3D molecular graphs due to the complexity of comparing 3D geometries and the lack of principled methods for handling this. This research addresses these issues.
This paper proposes a new AL paradigm specifically for 3D molecular graphs. It introduces novel 3D graph isometries for more accurate diversity sampling, leveraging distributions of 3D geometries to eliminate redundancy. A Bayesian geometric graph neural network efficiently computes uncertainties for sample selection. The active sampling is formulated as a quadratic programming problem, resulting in a computationally efficient framework. Experimental results demonstrate the effectiveness of the proposed approach.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in molecular learning and active learning, particularly those working with 3D molecular graphs. It provides a novel, principled active learning paradigm that significantly reduces annotation effort, a common bottleneck in the field. The introduced geometric graph isomorphisms and distributional representations advance the state-of-the-art in 3D graph analysis, opening avenues for more efficient and accurate model development. The quadratic programming approach offers a computationally efficient solution for sample selection. This work will influence future research on active learning for complex, 3D molecular data.
Visual Insights#

This figure illustrates the encoding process for molecular triangular and cross-angular isometries. Part A shows the triangular isometry, where angles are measured between a reference vector (from the centroid to the farthest atom) and vectors pointing to other atoms. Part B demonstrates the cross-angular isometry, which includes angles formed by any two atoms relative to the reference vector, providing a more comprehensive representation of 3D molecular geometry.
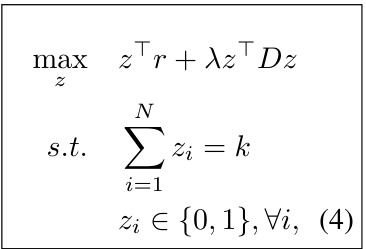
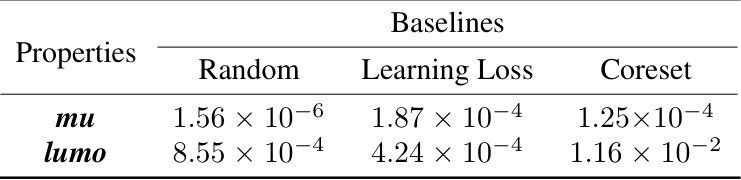
This table presents the p-values from paired t-tests comparing the performance of the proposed active learning method against four baseline methods (Random, Learning Loss, Coreset, Evidential Uncertainty) across four molecular properties (mu, alpha, homo, lumo). A p-value less than 0.05 indicates a statistically significant difference. The table shows the proposed method significantly outperforms all baselines across all properties.
In-depth insights#
3D Graph Isometry#
3D graph isometry, in the context of molecular representation learning, focuses on developing techniques to compare and classify 3D molecular structures based on their inherent geometric properties. This is a challenging problem because molecules are not rigid bodies and can exist in various conformations. A key aspect is defining suitable isometries – transformations that preserve relevant geometric features, such as distances between atoms, angles formed by atomic bonds, and overall molecular shape. These isometries are crucial for defining measures of similarity between molecules. The choice of isometries directly impacts the expressiveness of the resulting representation; more expressive isometries can better distinguish subtle differences in molecular geometry, which is critical for accurate predictions of molecular properties. Therefore, research in this area often involves designing novel isometries that provide a balance between expressiveness and computational efficiency, and rigorously analyzing their properties with respect to existing methods like the Geometric Weisfeiler-Lehman test (GWL) to demonstrate their effectiveness. The development of efficient algorithms for computing these isometries is also a major focus, as this is a computationally expensive task. The outcome of this research is improved 3D molecular graph representations that can be used in machine learning models for applications like drug discovery and materials science.
Bayesian GNNs#
Bayesian Graph Neural Networks (GNNs) represent a powerful paradigm shift in leveraging the strengths of both Bayesian methods and GNNs for improved uncertainty quantification and robustness. Bayesian methods excel at quantifying uncertainty, providing valuable insights into model confidence and aiding in decision-making, especially in scenarios with limited data or noisy observations. GNNs, on the other hand, are adept at capturing complex relationships and patterns within graph-structured data, making them well-suited for tasks involving molecules, social networks, knowledge graphs, and other relational data. The combination of these two powerful techniques results in models that are not only accurate but also provide measures of uncertainty associated with predictions. This is particularly important in high-stakes applications, such as medical diagnosis or drug discovery, where understanding uncertainty is crucial. A key aspect of Bayesian GNNs is the incorporation of prior knowledge or beliefs about the model parameters. This prior knowledge can help to regularize the model, improve generalization performance, and make the model more robust to noise and overfitting. Furthermore, Bayesian GNNs facilitate active learning strategies, enabling efficient and targeted data acquisition. By identifying data points where the model has high uncertainty, active learning focuses data collection efforts on the most informative samples, maximizing the impact of limited annotation resources.
Diversity Sampling#
Diversity sampling, in the context of active learning for 3D molecular graphs, aims to select a diverse subset of unlabeled molecules for annotation. This is crucial because including redundant samples doesn’t significantly improve model performance, while diverse samples provide more comprehensive information about the underlying data distribution. Effective diversity sampling methods must consider the 3D geometry of molecules, going beyond simple 2D structural comparisons, because the 3D structure significantly influences the chemical properties. The challenge lies in developing efficient and expressive methods to quantify the dissimilarity of molecules in 3D space, and this often involves computationally expensive techniques. A key aspect is selecting a measure of dissimilarity that captures the essential geometric features of molecules while being computationally feasible for large datasets. This often involves advanced graph isomorphism techniques or feature extraction methods that appropriately represent 3D structure. Ultimately, the goal of diversity sampling is to maximize information gain by strategically selecting molecules that represent the diversity in the dataset, thereby improving the model’s generalization ability and reducing annotation burden.
Active Learning AL#
Active learning (AL) in the context of 3D molecular graphs presents a unique opportunity to significantly reduce the annotation burden inherent in supervised learning approaches. The high computational cost associated with methods like density functional theory (DFT) makes traditional supervised learning impractical for large datasets. AL addresses this by strategically selecting the most informative samples for manual labeling. The key challenge lies in defining effective criteria for sample selection, balancing the need for maximizing uncertainty (samples where the model is least confident) with the need for diversity (avoiding redundant samples). The paper proposes an AL paradigm specifically tailored for 3D molecular graphs, leveraging novel 3D graph isometries and a Bayesian geometric graph neural network to quantify uncertainty. The resulting framework effectively combines diversity and uncertainty measures to choose the most beneficial samples for annotation, demonstrating improved efficiency and accuracy compared to baseline methods.
Future Directions#
Future research could explore extending the proposed active learning framework to encompass diverse molecular datasets, including larger-scale datasets and those with varied chemical properties. Investigating the framework’s performance with different 3D GNN architectures beyond SphereNet and DimeNet++ would further strengthen its generalizability. A crucial area for future investigation is the development of more sophisticated uncertainty quantification methods, potentially incorporating advanced Bayesian techniques or ensemble methods, to improve sample selection accuracy. Exploring different diversity metrics and their impact on AL performance warrants attention. Additionally, integrating the framework with other molecular property prediction methods could enhance its versatility. Finally, applying the framework to real-world drug discovery and materials science challenges is essential for demonstrating its practical value and identifying limitations in complex, real-world scenarios.
More visual insights#
More on figures

This figure shows two molecules, A and B, illustrating the concepts of triangular and cross-angular isometries. Both molecules share a similar overall structure, yet they differ in their precise 3D arrangement. The figure highlights how the choice of reference point (r1 and r2) and the relative positions of atoms (afar, ak, ai, aj) are crucial to encoding these isometries, particularly for computing the angles between vectors (such as v0 and vk) which is key to distinguishing the geometries of the molecules despite having similar planar structures.

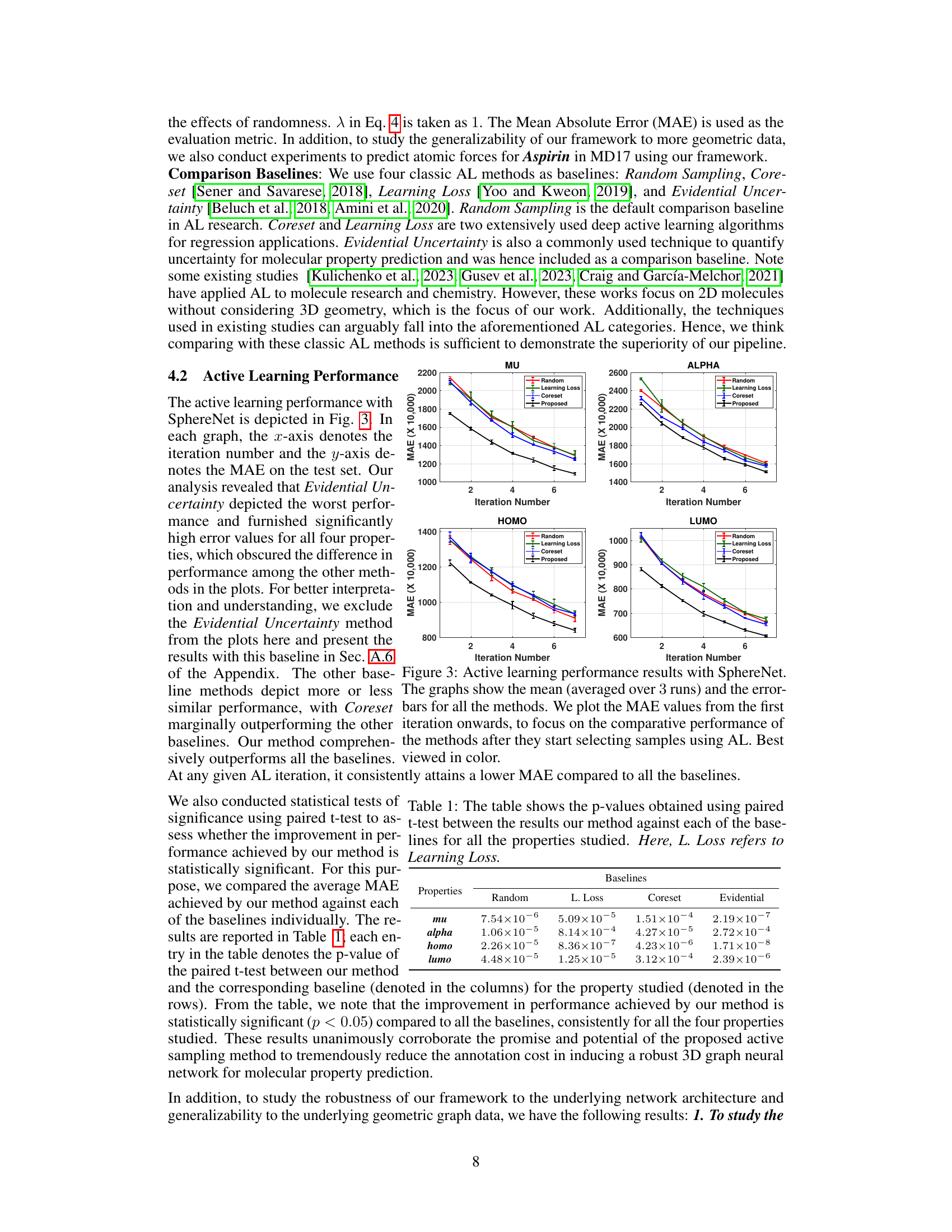
The figure presents the active learning performance results of the proposed method (using SphereNet) in comparison with four baseline methods across four different molecular properties (mu, alpha, homo, and lumo). Each graph shows the mean absolute error (MAE) on the test set plotted against the iteration number. The error bars represent the standard deviation over three runs. The results demonstrate the superior performance of the proposed approach after initial sample selection.
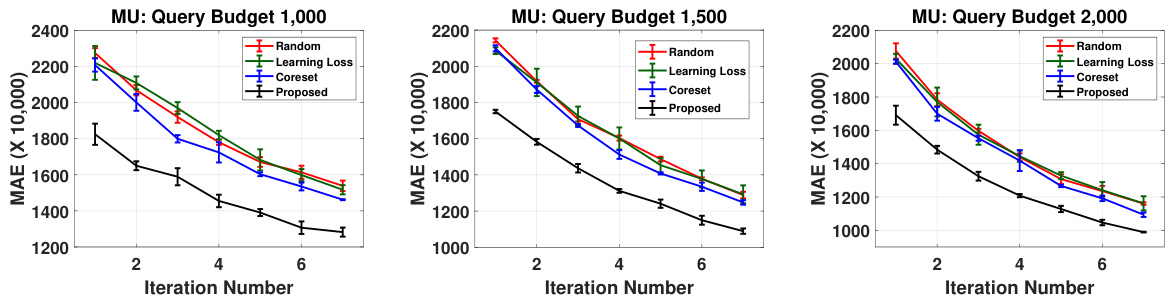
This figure shows the results of an experiment designed to evaluate the impact of different query budget sizes on the active learning performance of the proposed method and several baselines. The x-axis represents the iteration number, while the y-axis displays the mean absolute error (MAE) on a held-out test set. Three different query budget sizes (1000, 1500, and 2000) were tested, and the results for each are presented as separate subplots. Error bars represent the standard deviations obtained across three independent runs. The results demonstrate the consistency and robustness of the proposed method across different query budget settings.

This figure presents the ablation study results, comparing the performance of the proposed active learning framework against versions using only the uncertainty or diversity components. It demonstrates the synergistic effect of combining both uncertainty and diversity for improved performance in predicting the mu and lumo properties, highlighting that neither component alone achieves the same results as the combined approach.

This figure shows a flowchart of the active learning process used in the paper. It starts with an initial labeled dataset and an unlabeled dataset. The Bayesian Geometric Graph Neural Network (BGGNN) is trained on the labeled dataset. Then, the trained model is used to calculate an uncertainty score for each sample in the unlabeled dataset and a diversity matrix that describes the diversity between each pair of samples in the dataset. These scores and the matrix are then used in a quadratic programming (QP) problem to select a batch of k samples to be labeled. These samples are then added to the labeled set, and the unlabeled set is updated. The process is repeated iteratively.

This figure showcases the active learning performance of SphereNet for four properties (mu, alpha, homo, and lumo). The x-axis represents the iteration number (number of times samples are actively selected), and the y-axis depicts the mean absolute error (MAE) on a held-out test set. Error bars indicate the variability across three separate runs. The figure compares the performance of the proposed method against four baseline active learning approaches (Random Sampling, Core-set, Learning Loss, and Evidential Uncertainty). It highlights that the proposed approach consistently shows significantly lower MAE values than the baselines, demonstrating its effectiveness in improving active learning for 3D molecular graphs.

The figure presents the results of an active learning experiment using DimeNet++ as the backbone model. It compares the performance of the proposed method against several baselines (Random, Learning Loss, Coreset) across two properties (mu and lumo) from the QM9 dataset. The plots show Mean Absolute Error (MAE) values over seven AL iterations. Error bars represent the standard deviation across three experimental runs. The proposed method consistently outperforms baselines.

This figure shows the Mean Absolute Error (MAE) over iterations for four different active learning methods (Random, Learning Loss, Coreset, and the proposed method) using the SphereNet model. The x-axis represents the number of iterations, and the y-axis represents the MAE. Error bars are included to show variability in performance across the three runs. The results demonstrate that the proposed method consistently outperforms the baseline methods.
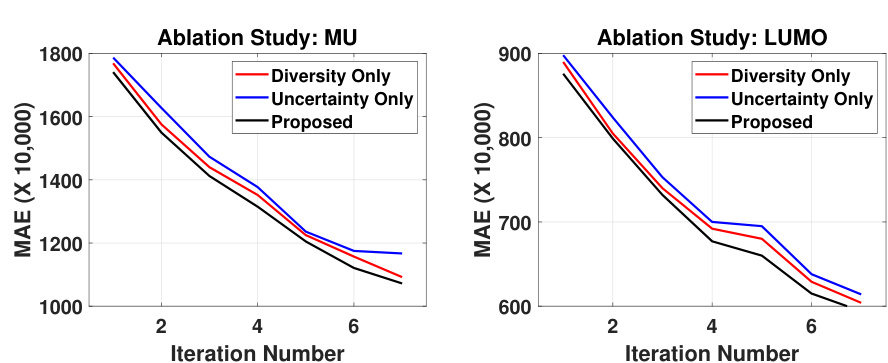
This figure presents the ablation study results on the mu and lumo properties using SphereNet. It compares the performance of the proposed method against two baseline methods: one using only the diversity component and the other using only the uncertainty component. The results show that the proposed method, which combines both diversity and uncertainty, outperforms both baselines, demonstrating the importance of both factors in achieving superior active learning performance.
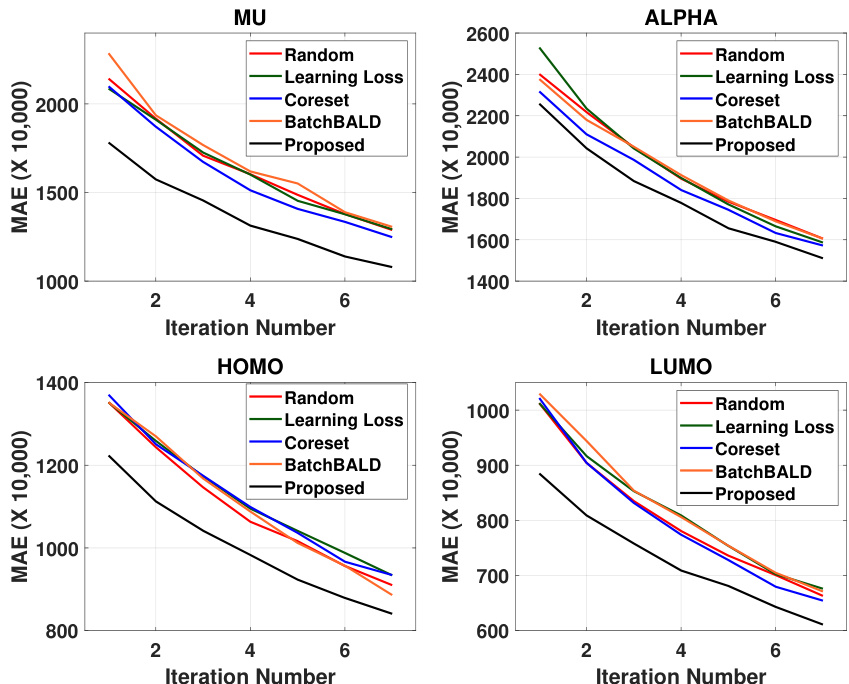
This figure presents the active learning performance results obtained using the SphereNet model on the QM9 dataset. It compares the performance of the proposed active learning method against several baseline methods (Random, Learning Loss, Coreset, BatchBALD). The x-axis represents the iteration number of the active learning process, and the y-axis shows the Mean Absolute Error (MAE) for four different molecular properties (mu, alpha, homo, lumo). The graph visually demonstrates the improvement in accuracy achieved by the proposed method across all four properties over multiple iterations. The use of color enhances the readability and understanding of the performance comparison.
More on tables

This table presents the p-values from pairwise t-tests comparing the proposed active learning method’s performance against several baseline methods (Random, Learning Loss, Coreset, Evidential Uncertainty) across four molecular properties (mu, alpha, homo, lumo). A p-value less than 0.05 indicates a statistically significant difference in performance.

This table shows the average time, in minutes, taken by each active learning method for one iteration of the active learning process. The methods are compared for the time taken for both the selection of samples and for training of the SphereNet model. The standard deviation is also reported alongside the average.
This table presents the p-values from paired t-tests comparing the performance of the proposed active learning method against three baseline methods (Random, Learning Loss, Coreset) for predicting two molecular properties (mu and lumo) using the DimeNet++ model as the backbone. Small p-values (typically less than 0.05) indicate statistically significant differences, suggesting that the proposed method outperforms the baselines.

This table presents the p-values from paired t-tests comparing the performance of the proposed active learning method against several baseline methods. The p-values indicate the statistical significance of the performance differences for the ‘mu’ property across three different query budgets (1000, 1500, and 2000). Lower p-values suggest a more significant improvement by the proposed method compared to the baselines.

This table presents the p-values from paired t-tests comparing the performance of the proposed active learning method against two ablation models: one using only the uncertainty component and the other using only the diversity component. The p-values indicate the statistical significance of the performance differences for predicting the ‘mu’ and ’lumo’ properties of molecules.

This table compares the performance of the proposed geometric descriptor with the SOAP descriptor for predicting the properties mu and lumo using SphereNet as the underlying GNN model. For each property, the Mean Absolute Error (MAE) is presented for seven AL iterations. ‘SOAP D’ refers to SOAP descriptor with diversity only, while ‘SOAP B’ indicates SOAP with both uncertainty and diversity. Similarly, ‘Our D’ and ‘Our B’ represent the proposed descriptor with diversity only and with both uncertainty and diversity respectively. The results show the effectiveness of the proposed descriptor compared to the SOAP descriptor.
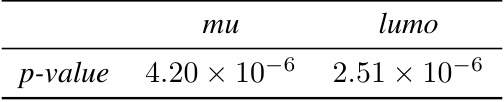
This table presents the p-values from paired t-tests comparing the performance of the proposed method against the SOAP descriptor for predicting the mu and lumo properties of molecules using the SphereNet model. The p-values indicate the statistical significance of the performance difference between the two methods.

This table presents the p-values from paired t-tests comparing the performance of the proposed active learning method against four baseline methods (Random, Learning Loss, Coreset, and Evidential Uncertainty) across four molecular properties (mu, alpha, homo, and lumo). Small p-values (typically <0.05) indicate statistically significant improvements of the proposed method over the corresponding baseline.

This table lists the assets used in the paper, their respective licenses, and a short description of what each asset is. The assets include pre-trained graph neural network models (SphereNet and DimeNet++), benchmark datasets (QM9 and MD17), and active learning schemes (Coreset, Learning Loss, and Evidential Uncertainty). The licenses are provided to ensure compliance and transparency in the use of these assets.
Full paper#