SCAFFLSA: Taming Heterogeneity in Federated Linear Stochastic Approximation and TD Learning

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it addresses the significant challenge of heterogeneity in federated learning, a critical issue limiting the scalability and efficiency of current methods. The proposed SCAFFLSA algorithm offers a significant improvement in communication complexity, enabling faster and more efficient model training in diverse settings. This work also provides novel theoretical insights into the impact of heterogeneity and offers new avenues for research in federated optimization and reinforcement learning.

Visual Insights

#

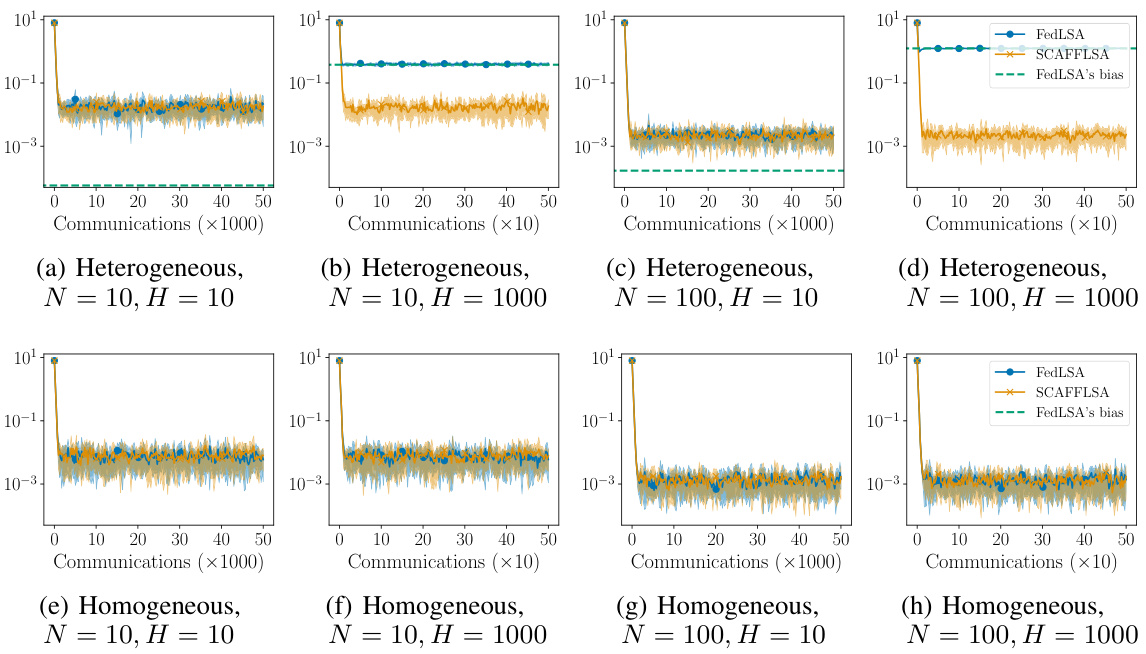
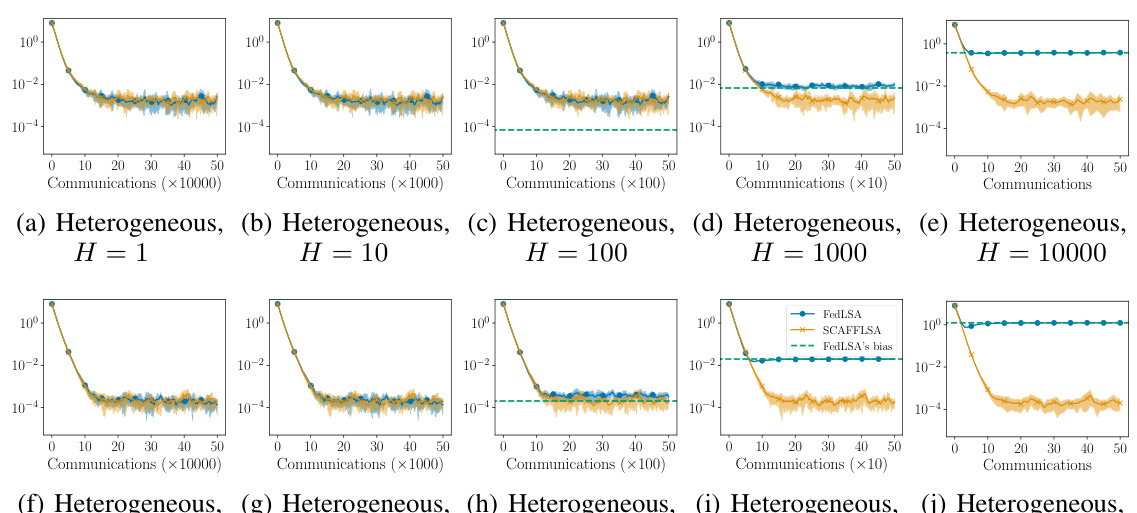
This figure compares the performance of FedLSA and SCAFFLSA algorithms on federated TD(0) with varying levels of heterogeneity. The plots show the mean squared error (MSE) as a function of the number of communication rounds. Different plots illustrate the results under different conditions: homogeneous versus heterogeneous agents, and different numbers of agents and local update steps. A key observation is that SCAFFLSA mitigates the bias inherent in FedLSA, leading to a significantly lower MSE, especially in heterogeneous settings.

This table presents the communication and sample complexities for three different algorithms: FedLSA, Scaffnew, and SCAFFLSA. It compares their performance in terms of how many communication rounds (T) and local updates (H) are needed to achieve a mean squared error (MSE) below a certain threshold ( ). The table highlights that SCAFFLSA achieves a logarithmic communication complexity compared to the polynomial complexity of FedLSA, while maintaining linear speedup in terms of sample complexity. The results for i.i.d. (independent and identically distributed) samples are shown, with a reference to Corollary 4.3 for complexities under Markovian assumptions.

In-depth insights

#

FedLSA Analysis

#

The heading ‘FedLSA Analysis’ suggests a section dedicated to a rigorous examination of the Federated Linear Stochastic Approximation (FedLSA) algorithm. This analysis likely involves a deep dive into the algorithm’s convergence properties, particularly focusing on its behavior under conditions of agent heterogeneity and its impact on communication efficiency. A key aspect would likely be the quantification of the algorithm’s bias, stemming from the differences in local data distributions across participating agents. The analysis would likely explore different scenarios, including i.i.d. (independent and identically distributed) data assumptions and Markovian noise sampling, providing comprehensive sample and communication complexity bounds. The mathematical techniques employed would probably include stochastic approximation theory and potentially martingale methods. Ultimately, the aim is to establish theoretical guarantees for FedLSA’s convergence while carefully characterizing the impact of heterogeneity on its performance. This would likely involve innovative theoretical arguments, especially regarding the achievement of linear speedup in sample complexity despite heterogeneity. The analysis may also include comparisons to related algorithms, highlighting the strengths and limitations of FedLSA in different settings.

SCAFFLSA Method

#

The SCAFFLSA method, a novel variant of FedLSA, is designed to address the communication complexity challenges inherent in federated learning, especially when dealing with heterogeneous agents. SCAFFLSA leverages control variates to correct for client drift, a common problem where agents diverge from the global optimum due to differences in their local training data. By incorporating control variates, SCAFFLSA significantly reduces bias and improves the convergence rate. The method achieves logarithmic communication complexity with respect to the desired accuracy, a substantial improvement over FedLSA’s polynomial scaling. This is particularly significant for large-scale federated learning where communication overhead is a major bottleneck. Furthermore, SCAFFLSA retains the linear speedup in sample complexity, indicating efficient use of data across multiple agents. The theoretical analysis of SCAFFLSA provides rigorous guarantees on its sample and communication complexity, making it a robust and efficient approach for solving systems of linear equations in heterogeneous federated learning environments.

TD Learning

#

The paper significantly contributes to the field of federated learning by analyzing and improving the Federated Linear Stochastic Approximation (FedLSA) algorithm, particularly in the context of temporal difference (TD) learning. It highlights how heterogeneity among agents impacts communication complexity in FedLSA for TD learning and introduces SCAFFLSA, a novel algorithm leveraging control variates to mitigate this issue. SCAFFLSA is shown to achieve logarithmic communication complexity and linear speedup, which is a significant improvement over the polynomial complexity of FedLSA. The theoretical analysis provides sample and communication complexity bounds for both algorithms, illustrating that SCAFFLSA effectively addresses heterogeneity bias while maintaining efficient training in the context of TD learning. The experimental results support the theoretical findings, demonstrating the effectiveness of SCAFFLSA in practical scenarios. The focus on TD learning with linear function approximation is noteworthy, as it addresses a key challenge in reinforcement learning, where efficient collaborative training is often limited by high variance and communication costs.

Complexity Bounds

#

The complexity bounds analysis in this research paper is crucial for understanding the efficiency of federated learning algorithms. The authors meticulously analyze both sample and communication complexities, providing theoretical guarantees on the convergence rate. This is particularly important in resource-constrained environments typical of federated settings, where minimizing communication overhead is paramount. The analysis reveals a polynomial scaling for FedLSA’s communication complexity with the inverse of the desired accuracy, which is a significant limitation. However, the introduction of SCAFFLSA, using control variates, dramatically improves this, achieving logarithmic scaling. This is a key contribution, demonstrating the effectiveness of bias correction techniques in improving communication efficiency. Furthermore, the study’s demonstration of linear speed-up with the number of agents is a major theoretical advancement, showing how the proposed algorithms benefit from distributed computation. The rigorous mathematical analysis supports these claims, and the numerical experiments validate the theoretical findings in various settings.

Future Work

#

Future research directions stemming from this work could explore several promising avenues. Extending the theoretical analysis to encompass more general settings beyond linear function approximation and i.i.d. data is crucial. Investigating the impact of different communication topologies and exploring decentralized variants of the proposed algorithms could yield valuable insights. Addressing practical challenges associated with real-world data heterogeneity in federated learning is another important area, as is developing methods to enhance robustness against adversarial attacks and stragglers. Empirically validating the theoretical findings on larger, more realistic datasets is essential, including those reflecting diverse real-world scenarios. Finally, further investigating the trade-off between communication efficiency and model accuracy will offer significant guidance for practical applications.

More visual insights

#

More on figures

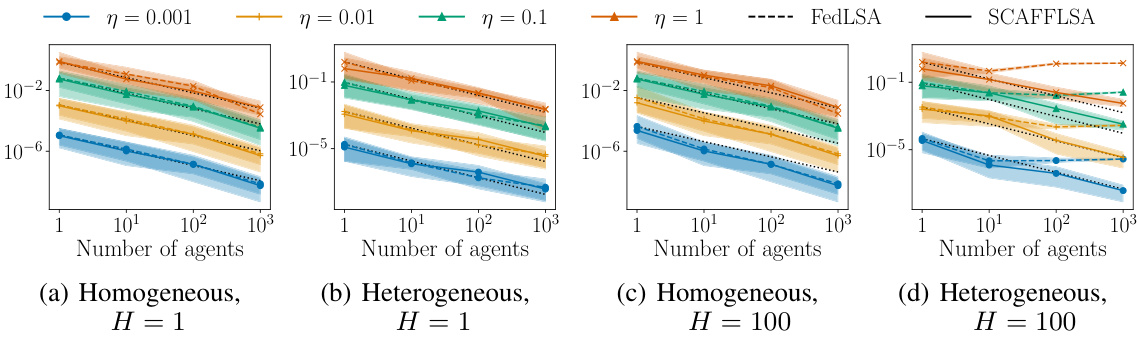
This figure compares the performance of FedLSA and SCAFFLSA in terms of Mean Squared Error (MSE) as the number of agents increases. The plot shows MSE in both homogeneous and heterogeneous settings for various step sizes. The black dotted line represents a 1/N decrease, which serves as a reference for linear speedup. The results demonstrate that both algorithms achieve linear speedup in the homogeneous setting. However, only SCAFFLSA maintains this speedup in heterogeneous settings, highlighting the benefits of SCAFFLSA’s bias correction technique.

This figure compares the performance of FedLSA and SCAFFLSA algorithms on federated TD(0) in terms of Mean Squared Error (MSE). The algorithms are tested in both homogeneous and heterogeneous settings with varying numbers of agents and local update steps. The green dashed line represents the bias predicted by Theorem 4.1 for FedLSA. The plots show MSE as a function of the number of communication rounds. For each configuration, the average MSE and variance across five runs are reported.

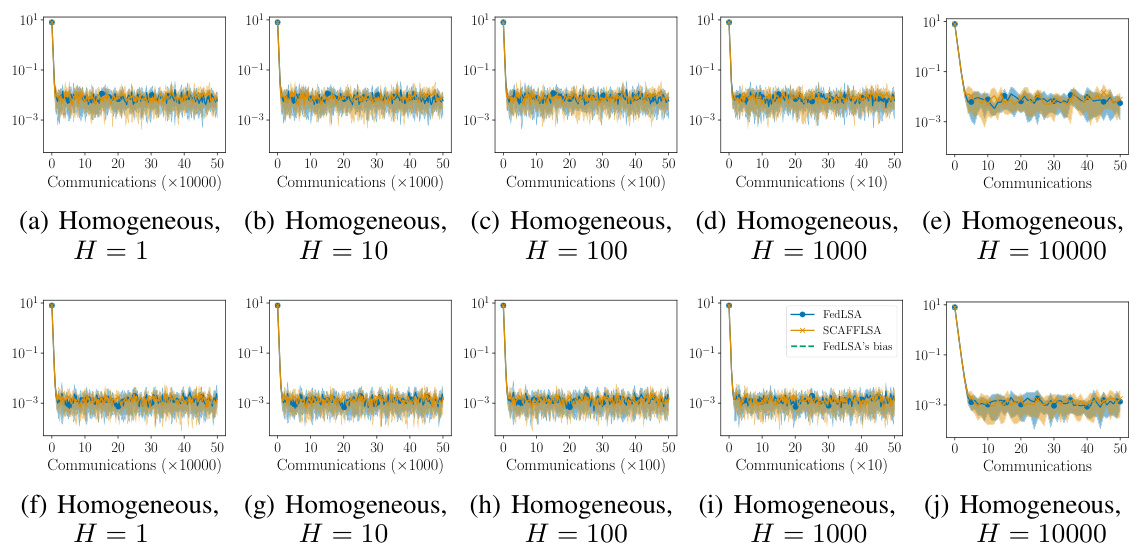
This figure compares the performance of FedLSA and SCAFFLSA on federated TD(0) in different settings. The x-axis represents the number of communication rounds, and the y-axis represents the mean squared error (MSE). Different plots show various combinations of heterogeneity (homogeneous vs. heterogeneous agents), number of agents (N), and number of local updates (H). The green dashed line shows the theoretical bias of FedLSA as predicted by Theorem 4.1. The figure demonstrates that SCAFFLSA generally outperforms FedLSA and is less sensitive to increases in the number of local updates (H), especially in heterogeneous settings.

This figure compares the performance of FedLSA and SCAFFLSA algorithms on federated TD(0) tasks under varying levels of heterogeneity (homogeneous vs. heterogeneous). Different numbers of agents (N = 10, 100) and local updates (H = 10, 1000) were tested. The green dashed line indicates the bias predicted by Theorem 4.1 for FedLSA. The results show the average MSE and variance across five runs for both algorithms. The plots illustrate how SCAFFLSA mitigates the bias inherent in FedLSA, particularly in heterogeneous settings, leading to improved MSE.

This figure compares the performance of FedLSA and SCAFFLSA algorithms on federated TD(0) for different settings. It demonstrates how the mean squared error (MSE) changes as a function of the number of communication rounds. The results are shown for both homogeneous (all agents have similar characteristics) and heterogeneous (agents have diverse characteristics) scenarios with different numbers of agents and different numbers of local updates. A green dashed line shows the bias of FedLSA, which is theoretically predicted. For each algorithm, the average MSE and variance are shown across 5 runs, offering a clear comparison between the two algorithms under various conditions.

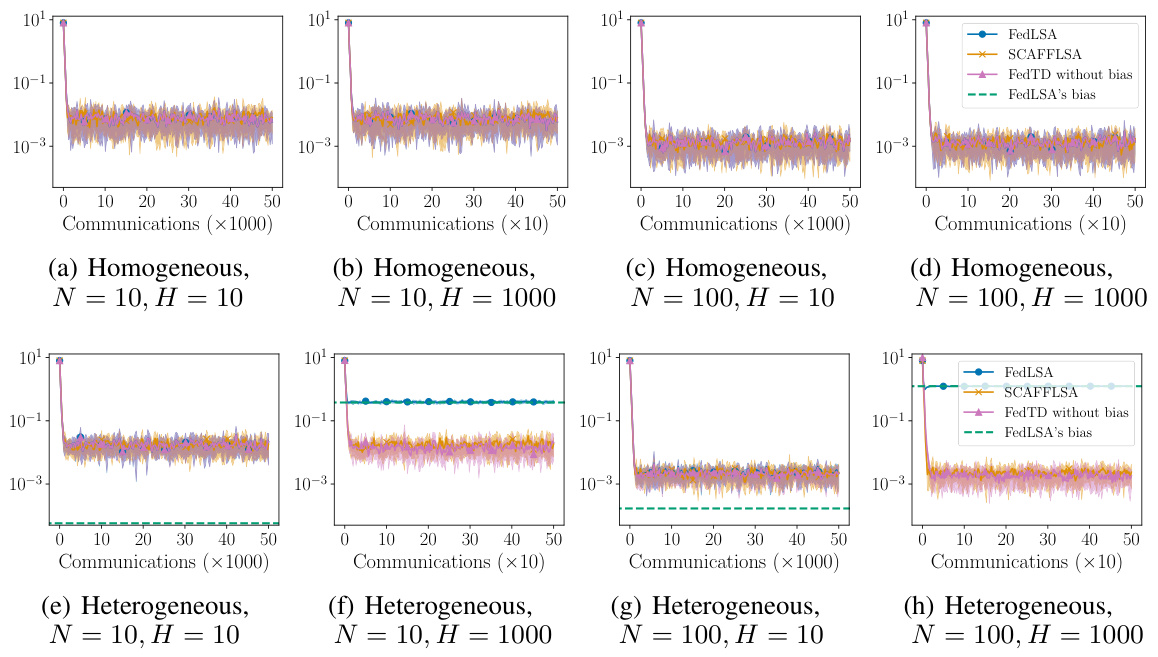
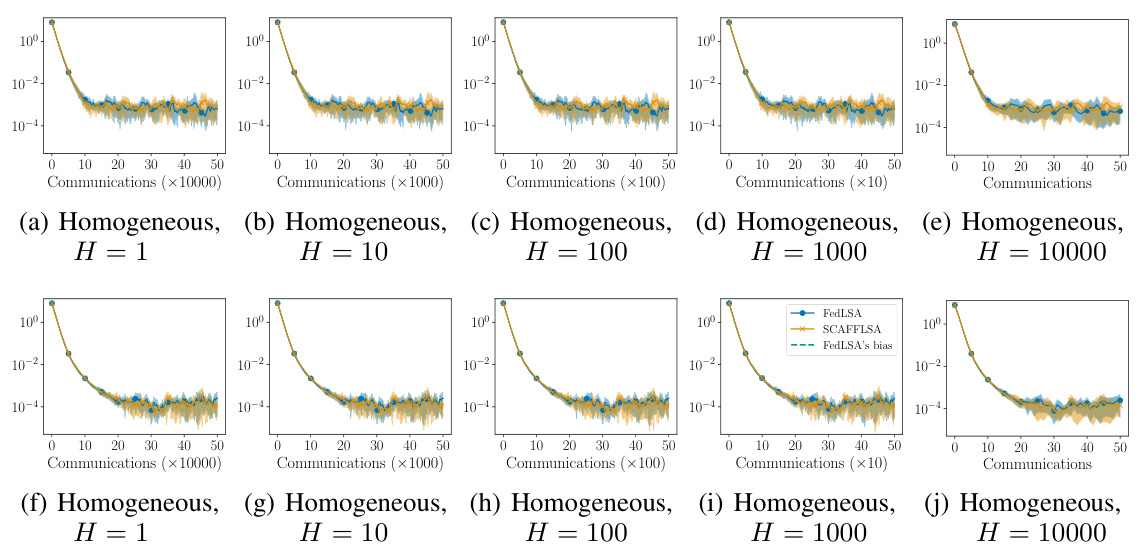
This figure compares the performance of FedLSA and SCAFFLSA algorithms on federated TD(0) tasks under different conditions. It showcases the mean squared error (MSE) over various communication rounds, varying the number of agents (N) and local updates (H). The plots illustrate how heterogeneity and the number of local updates affect the MSE. Notably, the green dashed line represents the bias inherent in FedLSA as predicted by Theorem 4.1. The figure shows that SCAFFLSA consistently outperforms FedLSA in heterogeneous settings by mitigating the bias.

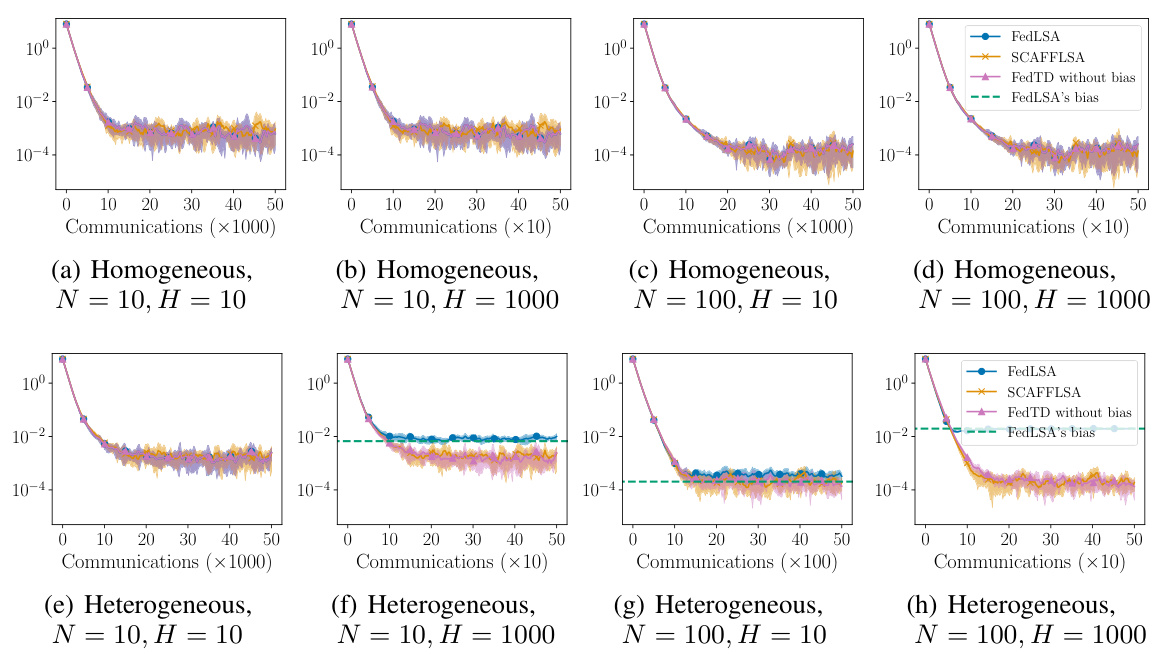
This figure compares the performance of FedLSA and SCAFFLSA algorithms on federated temporal difference (TD) learning. It shows the mean squared error (MSE) over a number of communication rounds for both homogeneous and heterogeneous settings. Different numbers of agents and local updates are considered. The green dashed line represents the bias of the FedLSA algorithm, highlighting how SCAFFLSA corrects for this bias, especially in heterogeneous scenarios. Error bars show the variance across multiple runs of each experiment.

More on tables

This table summarizes the communication and sample complexities for three algorithms: FedLSA, Scaffnew, and SCAFFLSA. It shows how these complexities scale with the desired accuracy (epsilon), the number of agents (N), and the number of local updates (H). A key finding highlighted is that FedLSA and its variant SCAFFLSA achieve linear speedup, meaning their sample complexity scales favorably with the number of agents.

This table summarizes the communication and sample complexity for three algorithms (FedLSA, Scaffnew, and SCAFFLSA) applied to the federated TD learning problem. It shows how the number of communication rounds, local updates, and sample complexity scale with respect to the desired accuracy (ε) and the number of agents (N). The key finding is that SCAFFLSA achieves logarithmic communication complexity with linear speedup, improving on the polynomial complexity of FedLSA.

Full paper

#