TL;DR#
In-context learning (ICL), where large language models (LLMs) learn new tasks from a few examples without parameter updates, is surprisingly effective but lacks theoretical understanding. Prior works focused on simpler models, neglecting the complex interplay of deep neural networks and attention mechanisms within LLMs. This raises the question of whether ICL’s success is just an empirical observation or reflects deeper, principled learning dynamics.
This paper bridges this gap by analyzing ICL using tools from statistical learning theory. The authors developed theoretical bounds for a transformer model comprising a deep neural network and a linear attention layer, trained on nonparametric regression tasks. They demonstrated that sufficiently trained transformers achieve near-minimax optimal risk, even improving upon optimal rates when task classes reside in coarser spaces. This suggests that successful ICL hinges on both the diversity of pretraining tasks and the ability of the model to effectively learn and encode relevant representations.
Key Takeaways#
Why does it matter?#
This paper is crucial because it provides a theoretical foundation for understanding the surprising effectiveness of in-context learning in large language models. It offers novel insights into the roles of pretraining and representation learning, paving the way for improved ICL algorithms and a deeper understanding of LLMs. This has significant implications for various AI research areas, including model optimization and few-shot learning.
Visual Insights#
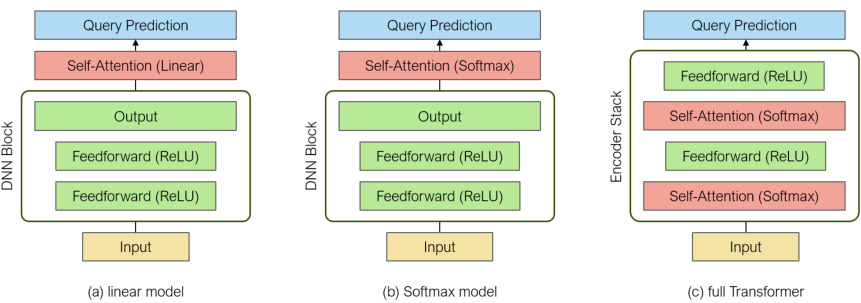
🔼 The figure shows the architecture of three different transformer models used in the paper’s experiments. Model (a) is a simplified linear model, (b) uses softmax attention, and (c) is a full transformer with two encoder layers. All models have two MLP components, single-head attention, and no layer normalization. The input dimension is 8, hidden layer widths and DNN output widths are 32. The query prediction is extracted from the last element of the model output.
read the caption
Figure 1: Architecture of the compared models. Each model contains two MLP components, all attention layers are single-head and LayerNorm is not included. (a),(b) implement the simplified reparametrization for attention, while all layers in (c) utilize the full embeddings. The input dimension is 8 and all hidden layer and DNN output widths are 32. The query prediction is read off the last entry of the output at the query position.
In-depth insights#
ICL Optimality#
The study explores the theoretical underpinnings of in-context learning (ICL) in large language models, focusing on its optimality. A key finding is that sufficiently trained transformers can attain near-minimax optimal estimation risk, even exceeding it under certain conditions. This optimality is demonstrated particularly within Besov spaces, achieving nearly dimension-free rates in anisotropic settings. Pretraining plays a crucial role, enabling the model to improve upon the a priori optimal rate by learning informative basis representations. The research rigorously establishes information-theoretic lower bounds, highlighting the joint optimality of ICL when pretraining data is ample but showing suboptimality when pretraining data is scarce. Task diversity emerges as a significant factor, influencing the attainment of optimal ICL performance. This work provides a deeper, statistical learning theory-based understanding of why ICL works effectively, extending the existing knowledge beyond single-layer linear models. However, the model analyzed is a simplified version of a transformer, leaving open questions regarding complex, multi-layer architectures.
Transformer ICL#
The concept of “Transformer ICL” combines the architectural strengths of transformer networks with the intriguing phenomenon of in-context learning (ICL). Transformers, known for their ability to capture long-range dependencies in sequential data through self-attention mechanisms, are well-suited for ICL tasks. ICL leverages a model’s pre-trained knowledge to perform new tasks by simply providing a few examples in the input prompt, without explicit retraining. Analyzing “Transformer ICL” involves exploring how the transformer architecture facilitates ICL, examining the role of pre-training on the model’s capacity for few-shot learning and investigating the generalization properties of this approach. Key questions include: how does the depth and architecture of the transformer impact its ability to perform ICL? How does the nature of the pre-training data affect ICL performance? Understanding the theoretical underpinnings of this combined approach is crucial. Formal analysis can provide insights into the factors driving ICL success in transformers and contribute to improved model designs and training strategies.
Besov Space ICL#
The concept of ‘Besov Space ICL’ merges the mathematical framework of Besov spaces with the machine learning paradigm of in-context learning (ICL). Besov spaces offer a versatile tool for analyzing function smoothness, capturing both local and global regularity, unlike simpler spaces like Sobolev or Hölder spaces. Applying Besov spaces to ICL provides a rigorous way to analyze the performance of large language models (LLMs) on few-shot learning tasks. This allows researchers to determine optimal learning rates and understand the impact of factors like model depth, data diversity, and context length on the model’s ability to generalize. A key insight here is that the minimax optimal learning rate in Besov spaces is achievable by sufficiently trained transformers in ICL settings. This finding is particularly significant as it establishes a theoretical foundation for the empirical success of LLMs in few-shot learning. Further research could explore the influence of specific hyperparameters within the transformer architecture and the relationship between task diversity and the effective dimensionality of the Besov space in determining the model’s generalization capabilities. Ultimately, a detailed understanding of Besov space ICL is crucial for developing more efficient and effective LLMs.
Minimax Bounds#
The minimax bounds analysis in this research paper is crucial for understanding the fundamental limits of in-context learning (ICL). The authors derive both upper and lower bounds on the estimation error, characterizing the best possible performance of any ICL algorithm under specific conditions. These bounds are expressed in terms of several key factors including sample size, the number of tasks, and the complexity of the underlying function class. The upper bounds provide guarantees on the performance of the proposed transformer model, demonstrating its ability to achieve near-optimal rates under sufficient pretraining. The lower bounds, on the other hand, establish fundamental limitations, proving that no algorithm can substantially outperform the obtained bounds. This two-sided analysis is a significant contribution because it sheds light on the role of pretraining, sample size, and diversity in ICL’s success and offers insights into its inherent limitations.
Future ICL#
Future research in In-Context Learning (ICL) should prioritize rigorous theoretical understanding of its mechanisms, moving beyond empirical observations. Addressing the limitations of current models, such as their sensitivity to prompt engineering and the need for massive pretraining datasets, is crucial. Exploring the connections between ICL and other meta-learning paradigms could lead to more efficient and robust algorithms. Furthermore, investigating the impact of architectural choices on ICL capabilities is essential, potentially uncovering more efficient architectures for few-shot learning. Finally, research must focus on developing ICL techniques for broader applications, such as addressing task heterogeneity and extending to complex, real-world scenarios beyond benchmark datasets.
More visual insights#
More on figures
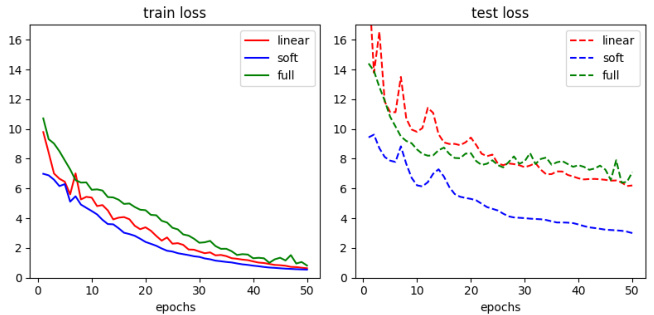
🔼 This figure shows the training and testing loss curves for three different transformer models during the pretraining phase of in-context learning. The models are: a linear model, a softmax model, and a full transformer model. The Adam optimizer was used with a learning rate of 0.02 for all layers. The task class parameters were set to a=1, p=q=∞, T=n=512. Samples were generated from random combinations of order 2 wavelets. The plot shows that all three models converge to a low training loss, demonstrating the effectiveness of the pretraining procedure.
read the caption
Figure 2: Training and test curves for the ICL pretraining objective. We use the Adam optimizer with a learning rate of 0.02 for all layers. For the task class we take a = 1, p = q = ∞, T = n = 512 and generate samples from random combinations of order 2 wavelets.
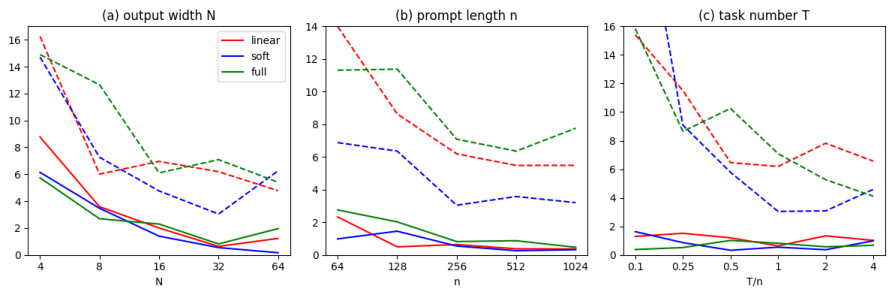
🔼 This figure shows the training and test losses of three different transformer models after 50 training epochs. The models are compared under varying conditions: (a) changes in the width of the deep neural network (DNN) layer, (b) changes in the number of in-context examples, and (c) changes in the number of training tasks used for pretraining. The results are shown as median values over 5 runs to highlight robustness. The figure demonstrates how model performance is affected by these various parameters.
read the caption
Figure 3: Training and test losses of the three models after 50 epochs while varying (a) DNN width N; (b) number of in-context samples n; (c) number of tasks T. For (a), the widths of all hidden layers also vary with N. We take the median over 5 runs for robustness.
Full paper#



















