↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Variational inference, a widely used technique in machine learning for approximating complex probability distributions, typically relies on Kullback-Leibler (KL) divergence. However, KL divergence has limitations, notably its tendency to underestimate variance, leading to suboptimal results. Recent works have explored alpha-divergence, a more general family of divergences that offers flexibility in adjusting the trade-off between accuracy and variance, but a theoretical understanding of its asymptotic properties has been lacking. This research directly addresses this gap.
This research focuses on the convergence properties of alpha-divergence minimization algorithms. It establishes sufficient conditions to guarantee convergence to a local minimum at a geometric rate, particularly for exponential families. The paper also introduces a novel unbiased algorithm that overcomes the limitations of previous biased gradient estimators. This unbiased approach is proven to converge almost surely to a local minimum with a given convergence rate. The work then extends the algorithm to variational autoencoders (VAEs) and presents a detailed empirical analysis demonstrating the improved performance of the novel algorithm over existing methods for both toy and real datasets, providing detailed proofs of convergence and rates.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in variational inference. It provides rigorous theoretical guarantees for alpha-divergence minimization algorithms, addressing a critical gap in the existing literature. This work also opens new avenues for developing more robust and efficient variational inference methods, impacting various machine learning applications.
Visual Insights#
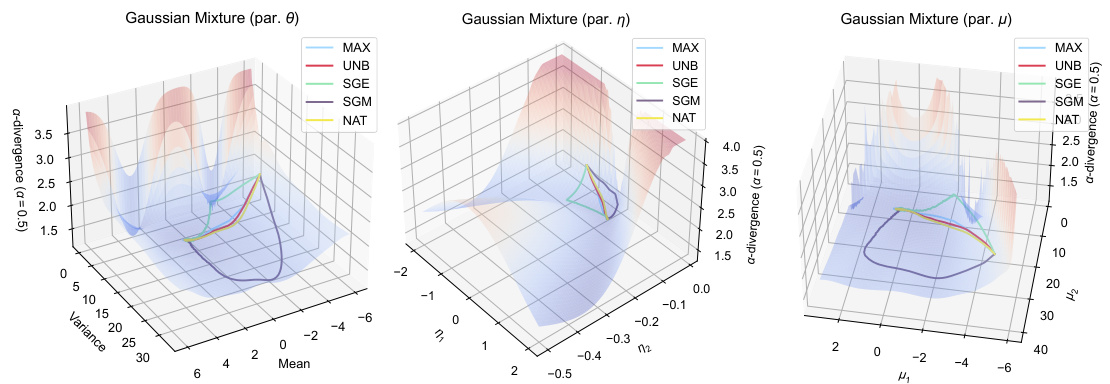
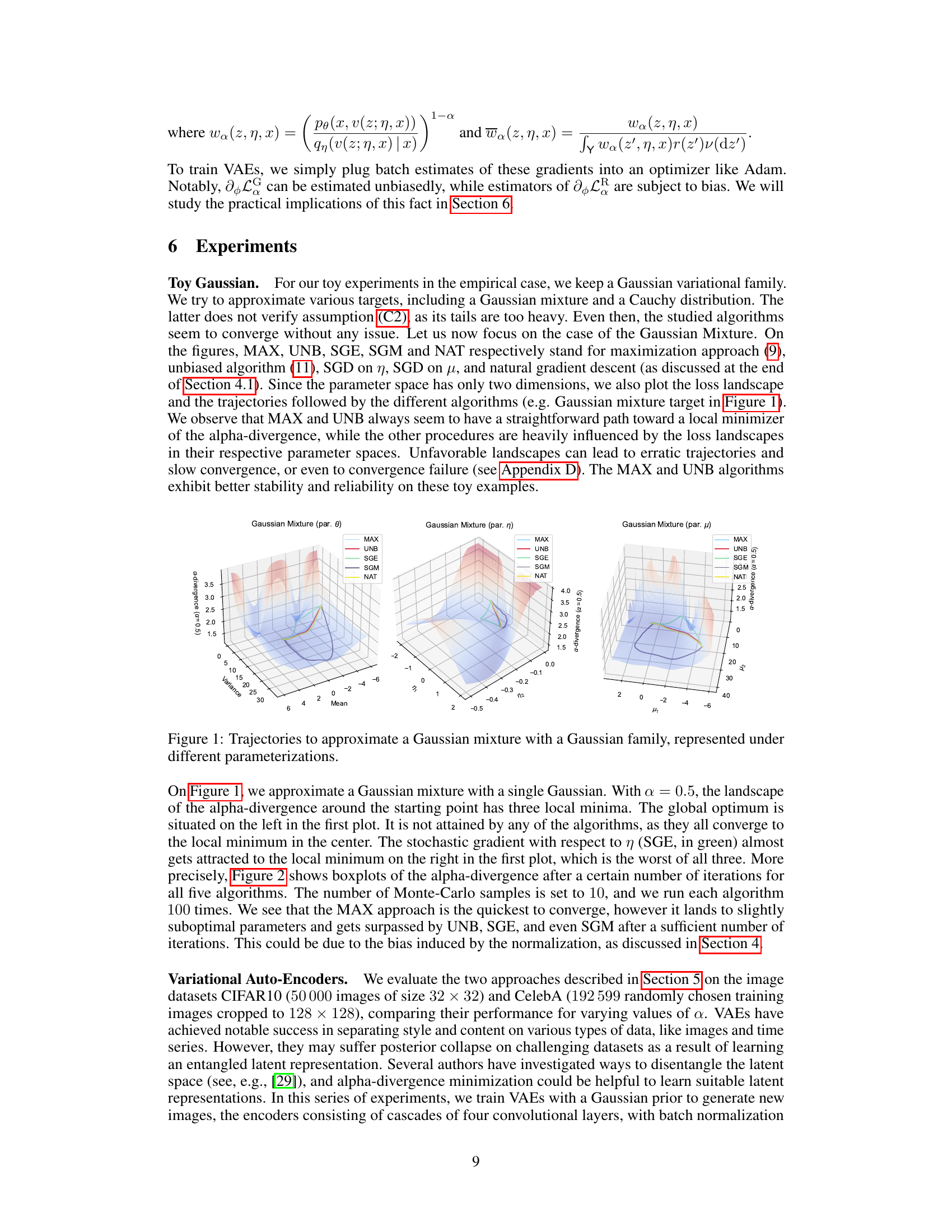
This figure displays the trajectories of five different variational inference algorithms (MAX, UNB, SGE, SGM, NAT) while approximating a Gaussian mixture target using a single Gaussian family. The three subplots represent the trajectories in three different parameter spaces: the original parameters (θ), the natural parameters (η), and the mean parameters (μ). Each subplot shows how the algorithms converge to a local minimum of the alpha-divergence. The different colors represent the different algorithms, and the shaded surface represents the alpha-divergence landscape. The figure illustrates the impact of parameterization on algorithm behavior and convergence paths.
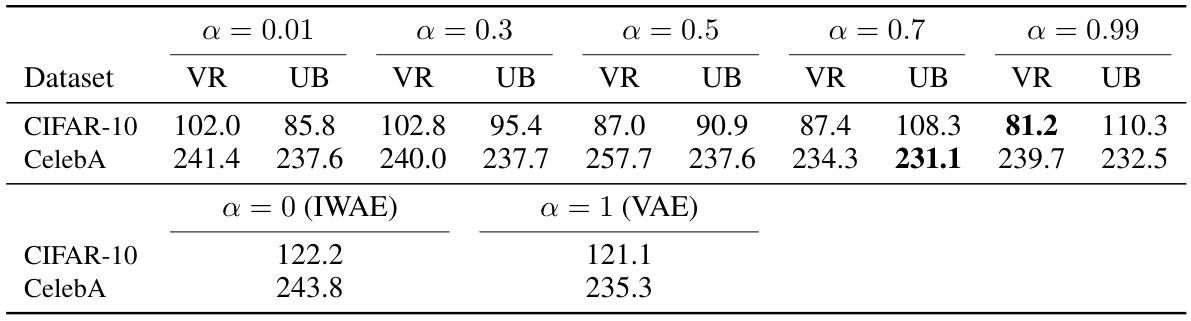
This table presents the Fréchet Inception Distance (FID) scores, a metric for evaluating the quality of generated images, for different variational autoencoder (VAE) models trained using the biased and unbiased alpha-divergence minimization algorithms. The results are shown for various values of the alpha parameter (α) and for two datasets: CIFAR-10 and CelebA. Lower FID scores indicate better image generation quality. The table also includes results for the IWAE (α=0) and standard VAE (α=1) baselines for comparison.
In-depth insights#
α-Divergence Theory#
Alpha-divergence, a family of divergences generalizing the Kullback-Leibler divergence, offers flexibility in variational inference by controlling the balance between model accuracy and variance. Lower values of α emphasize inclusive KL, encouraging exploration and potentially mitigating the zero-forcing effect seen in standard variational approaches. Conversely, higher α values approach exclusive KL, leading to more precise but potentially overconfident models. The theoretical analysis of alpha-divergence methods is challenging due to the non-convexity of the objective function. Convergence proofs often rely on specific assumptions about the model family (like exponential families) and the optimization procedure. Establishing convergence rates and characterizing asymptotic behavior are crucial aspects of the theoretical development, providing important guarantees for practical applications. The research likely investigates whether the convergence is to a global optimum or merely a local one and explores the effect of different α values on the final model, its bias, and variance.
Algo Convergence#
The paper delves into the asymptotic behavior of alpha-divergence variational inference algorithms, focusing on their convergence properties. A key aspect is the analysis of a monotonic algorithm, proving its convergence to a local minimizer at a geometric rate under specific conditions, particularly when the variational family belongs to exponential models. The algorithm’s convergence is rigorously established, offering a theoretical guarantee not often found in similar works. However, the study also acknowledges the challenges in directly applying this ideal algorithm to real-world scenarios due to biased gradient estimators. Consequently, an unbiased alternative is proposed and its almost sure convergence is demonstrated. This unbiased version, backed by a law of the iterated logarithm, provides stronger theoretical support for practical applications. The analysis highlights crucial assumptions and limitations, paving the way for a more robust understanding of alpha-divergence methods within variational inference.
Unbiased Algorithm#
The core of this research paper revolves around addressing the limitations of biased gradient estimators commonly used in alpha-divergence variational inference. The authors recognize that these estimators hinder theoretical analysis and propose an unbiased alternative. This unbiased algorithm, unlike its biased counterpart, converges almost surely to a local minimizer of the alpha-divergence, a crucial improvement. The theoretical foundation is solidified by a proof of almost sure convergence and a law of the iterated logarithm, offering strong guarantees on the algorithm’s behavior. The algorithm’s unbiased nature enhances its reliability and allows for a more rigorous analysis of its convergence properties, paving the way for more robust variational inference applications. Furthermore, the authors elegantly connect their unbiased algorithm to the framework of Robbins-Monro algorithms, providing a clearer understanding of its behavior and facilitating further investigation. The paper validates the effectiveness of the unbiased algorithm through experimentation on both synthetic and real-world datasets, demonstrating its superior stability and performance compared to other methods.
VAE Application#
The section on VAE application demonstrates a practical extension of the core alpha-divergence variational inference methods. It cleverly adapts the biased and unbiased algorithms to the training of Variational Autoencoders (VAEs), showcasing their applicability to a complex, widely-used model. The key insight is the connection established between the algorithms and variational bounds (VR and LG), providing a principled justification for their use in this setting. This effectively transforms the alpha-divergence minimization into a gradient ascent procedure on these bounds, allowing for a straightforward optimization within the VAE framework. The authors further demonstrate how to maximize these bounds using the reparameterization trick for practical implementation and discuss the bias inherent in estimating certain gradient components, a critical consideration in the context of VAE training and model performance. This section highlights the practical impact of the theoretical findings, showcasing a significant application of the developed methods. Finally, empirical results using the proposed algorithms on real-world image datasets (CIFAR-10 and CelebA) provide compelling evidence of the method’s efficacy. The inclusion of FID scores offers a robust and relevant metric to assess the generated images’ quality, enabling direct comparison between different settings and algorithms. This section contributes to the field by showing a successful implementation in a challenging domain that leverages the theoretical advancements.
Empirical Results#
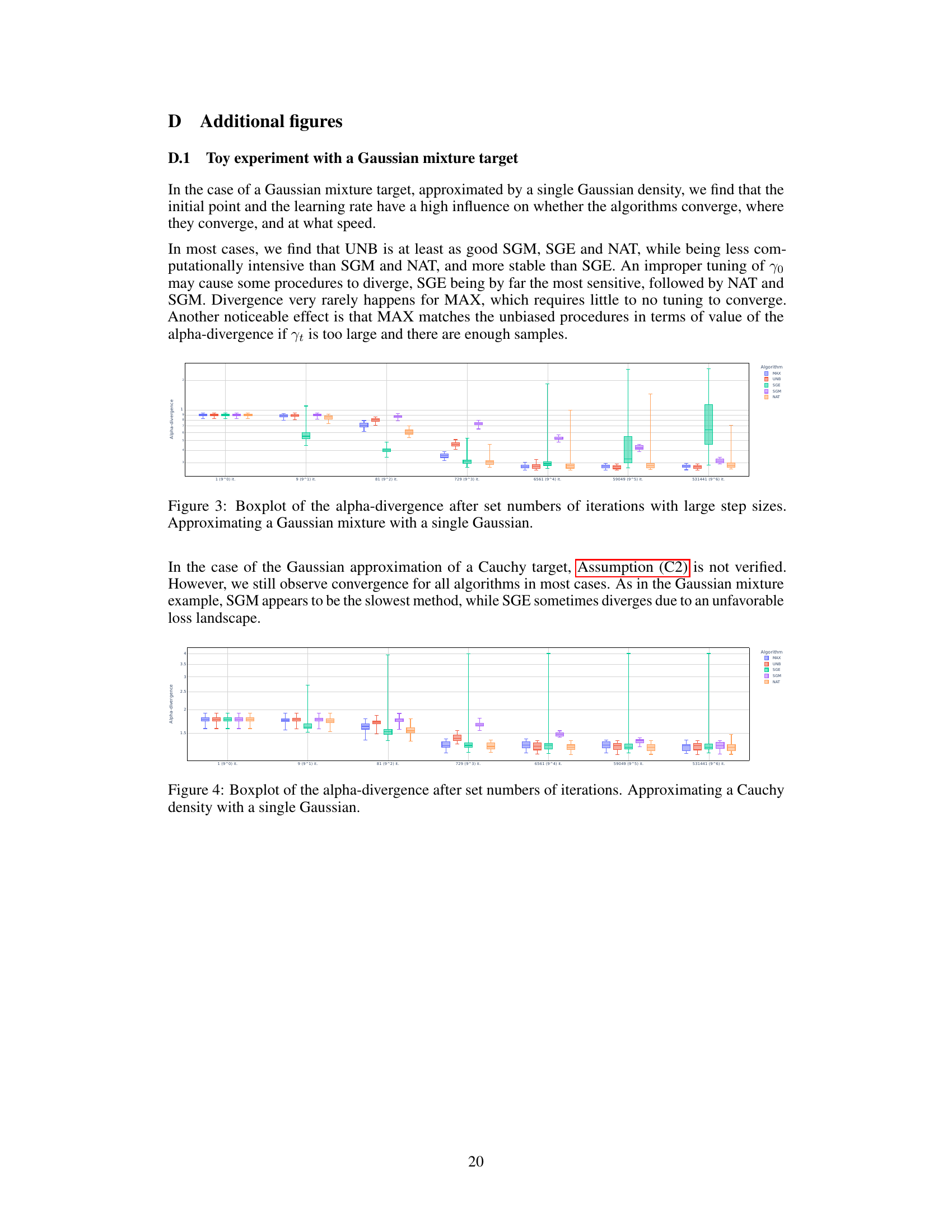
An effective ‘Empirical Results’ section would begin by clearly stating the goals of the empirical study. It should then present the datasets used, clearly describing their characteristics and limitations. The chosen evaluation metrics should be justified and results presented using appropriate visualizations such as tables and figures, including error bars. Crucially, the results section should directly address the claims made in the introduction and provide a clear comparison to relevant baselines. Any unexpected or anomalous results should be discussed, acknowledging limitations and potential biases in the methodology. Finally, the section should provide a concise summary of the key findings, highlighting any significant insights or novel observations that emerged from the empirical analysis. A discussion of limitations and potential future work should also be included to foster a comprehensive understanding of the study’s scope and contribution.
More visual insights#
More on figures
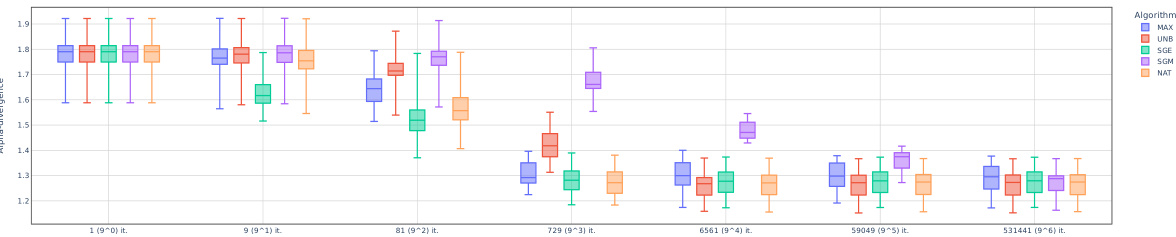
This figure visualizes the performance of five different variational inference algorithms (MAX, UNB, SGE, SGM, NAT) in approximating a Gaussian mixture distribution using a Gaussian variational family. The trajectories of each algorithm’s parameters (mean and variance) are plotted across iterations, showcasing their convergence behavior toward a local minimum of the alpha-divergence. The three subplots represent different parameterizations (Gaussian mixture parameters, Gaussian family parameters using natural parameters η, and Gaussian family parameters using mean parameters μ). The figure highlights the different convergence behaviors of the algorithms under different parameterizations and loss landscapes, with MAX and UNB demonstrating more direct paths towards local minima compared to the other algorithms, which exhibit more erratic trajectories due to unfavorable landscapes.

This figure compares the performance of five different algorithms (MAX, UNB, SGE, SGM, NAT) in approximating a Gaussian mixture using a Gaussian family. Each algorithm’s trajectory in the parameter space is shown for both parameterizations (η and μ). The alpha-divergence (a=0.5) is used as the objective function. The figure highlights the different convergence behaviors and paths toward a local minimum of the alpha-divergence for each algorithm. The variations in trajectories reflect the algorithms’ sensitivity to the loss landscape and the chosen parameterization.

This figure visualizes the trajectories of five different variational inference algorithms (MAX, UNB, SGE, SGM, NAT) while approximating a Gaussian mixture using a Gaussian family. Each algorithm’s path through the parameter space is shown for three different parameterizations (par. 0, par. η, par. μ), providing a visual comparison of their convergence behavior. The alpha-divergence (with α=0.5) is used as the optimization criterion. The different trajectories highlight the impact of algorithm choice and parameterization on convergence speed and final result.
Full paper#