↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current diffusion models for solving inverse problems are computationally expensive and require vast amounts of data, especially for high-resolution images like those in 3D medical imaging. This limits their applicability to many real-world problems. The significant cost associated with training these models and the large memory requirement for inference creates a major bottleneck.
To address these issues, the researchers developed PaDIS, a patch-based diffusion inverse solver. PaDIS trains a diffusion model on image patches instead of whole images, significantly reducing both computational cost and data requirements. Importantly, it leverages positional encoding to generate complete, high-resolution images during inference, while maintaining high accuracy in solving various inverse problems such as CT reconstruction, deblurring, and super-resolution. The results demonstrate PaDIS’s superior performance, particularly with limited training data, showcasing its data efficiency.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on high-dimensional inverse problems, especially in medical imaging. It introduces a highly efficient training method that significantly reduces computational cost and data requirements, making it applicable to large-scale problems previously considered infeasible. The proposed technique’s flexibility in pairing with various inverse solvers opens doors for broader applications and future research into effective data-efficient priors.
Visual Insights#
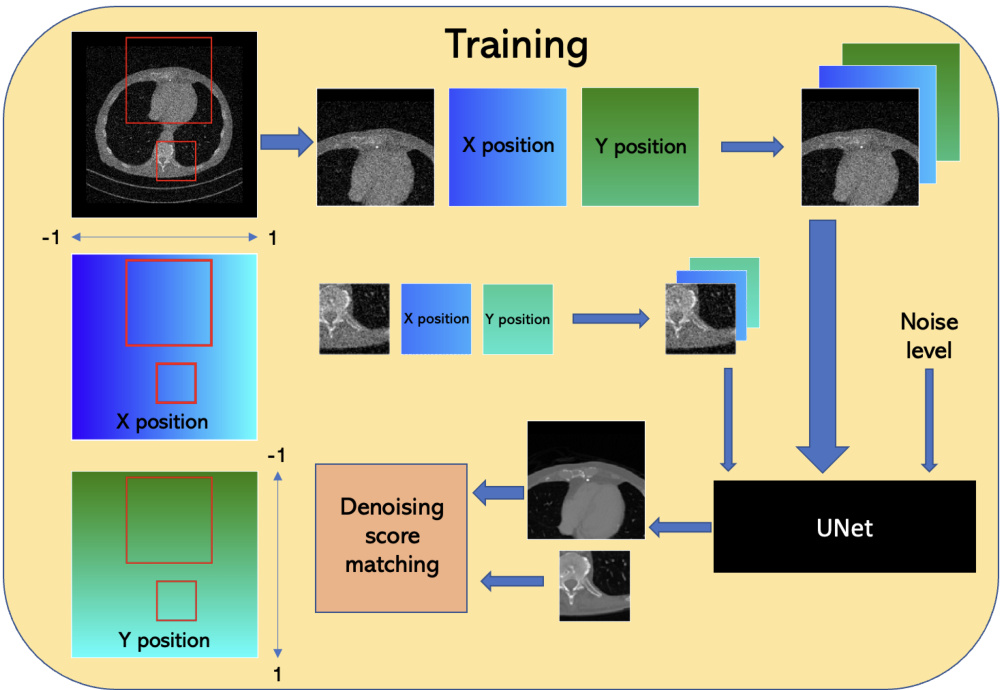
The figure illustrates the training process of the PaDIS method. It shows how different sized image patches are extracted from the training images. For each patch, the x and y coordinates of each pixel are normalized and appended to the patch as additional channels. These patches with positional information are then fed into a UNet to learn the denoising score function. The noise level is also inputted to the UNet during training.

This table presents a quantitative comparison of different methods for solving three inverse problems: CT reconstruction with 8 and 20 views, image deblurring, and image super-resolution. The methods compared include baselines (FBP, ADMM-TV, PnP-ADMM, PnP-RED), a whole-image diffusion model, and the proposed PaDIS method along with several sampling algorithms. The results are presented as average PSNR and SSIM values across all test images. The bold values indicate the best performing method for each inverse problem.
In-depth insights#
Patch-Based Priors#
The concept of ‘Patch-Based Priors’ in image processing offers a compelling approach to address computational and data limitations associated with traditional diffusion models. By training models on image patches rather than entire images, memory efficiency and training speed are significantly enhanced, making it feasible to handle high-resolution and high-dimensional data. This approach reduces the need for extensive datasets, as numerous patches can be extracted from a relatively small number of images. The use of positional encoding is crucial for maintaining the ability to reconstruct the complete image from its individual components, ensuring that the global structure and inter-patch relationships are preserved. The effectiveness of patch-based priors is demonstrated through their ability to improve the efficiency and performance across various inverse problems, such as CT reconstruction and image deblurring, particularly in scenarios with limited training data. Generalizability is another notable aspect because the learned patch priors can be combined with various sampling techniques and inverse problem solvers, increasing the overall utility of the method.
PaDIS Framework#
The PaDIS framework presents a novel approach to learning efficient image priors for solving inverse problems. Its core innovation lies in training diffusion models on image patches rather than entire images, significantly reducing computational costs and data requirements. This patch-based strategy is coupled with positional encoding, allowing the model to effectively reconstruct whole images from the learned patch-level representations. The framework demonstrates high flexibility, readily pairing with various diffusion inverse solvers and sampling methods. Improved memory efficiency and data efficiency are key advantages, enabling the application of PaDIS to high-dimensional and high-resolution data where traditional methods struggle. The effectiveness of PaDIS is validated through its successful application to diverse inverse problems, such as CT reconstruction, deblurring, and super-resolution, showcasing its generalizability and robustness.
Inverse Problem#
Inverse problems, where the goal is to infer a hidden cause from observed effects, are pervasive in imaging science. The paper tackles these challenges by leveraging the power of diffusion models to learn strong image priors. The core idea revolves around training these models on image patches instead of whole images, which drastically enhances computational efficiency and reduces data requirements. This strategy allows for effective processing of high-dimensional data such as 3D images. The authors propose a novel method, PaDIS, which cleverly combines the learned patch-level priors with positional encoding to reconstruct entire images. This patch-based approach is highly flexible, enabling the use of various diffusion models and inverse problem-solving techniques. Importantly, the paper demonstrates PaDIS’s superior performance, especially with limited training data, on multiple inverse problems including CT reconstruction, deblurring, and super-resolution. The results highlight the significant potential of patch-based diffusion models in addressing the computational bottlenecks that hamper many applications of deep learning in medical and natural image analysis. Furthermore, the study highlights the method’s capability to solve a broad range of problems, emphasizing its potential across diverse imaging modalities.
Ablation Studies#
Ablation studies systematically remove or alter components of a model to assess their individual contributions. In this context, the researchers likely investigated the impact of various parameters on the performance of their patch-based diffusion model. This could involve examining the effect of patch size, dataset size, and positional encoding. Analyzing the results would reveal insights into the model’s robustness, efficiency, and the critical factors driving its performance. For instance, smaller patch sizes might improve computational efficiency but could harm the accuracy of the global image reconstruction, revealing a trade-off between speed and accuracy. Similarly, examining the impact of data size helps understand the model’s generalization ability and its susceptibility to overfitting. Finally, evaluating the importance of positional encoding would highlight its necessity for holistic image generation, demonstrating whether the spatial information is crucial for capturing global image context.
Future Works#
Future research directions stemming from this work on patch-based diffusion models for inverse problems could explore several avenues. Scaling to even higher-dimensional data (e.g., 4D or higher) would be a significant advance, possibly leveraging advanced parallel computing techniques or more efficient network architectures. Investigating alternative patch sampling strategies could enhance image quality and reduce artifacts. The current approach shows great promise, but further improvements in sample efficiency are crucial for practical applications, especially in medical imaging where computational resources are often limited. Exploring novel architectures or loss functions to improve the data efficiency of the patch-based models would also be a valuable next step. Finally, investigating the potential for incorporating learned priors into other image processing and computer vision tasks warrants further study. The flexible nature of the learned prior suggests broader applications beyond the examples demonstrated here.
More visual insights#
More on figures
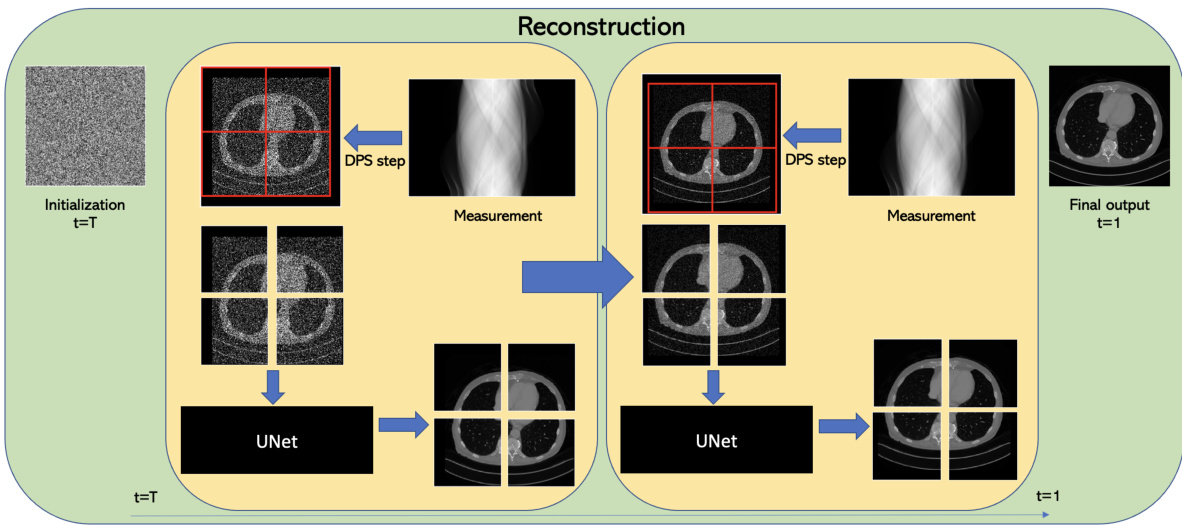
This figure illustrates the reconstruction process of the PaDIS method. It begins with pure noise at time t=T. At each step, a random partition of the zero-padded image is selected, and a neural network (trained on image patches) computes the score function for the entire image. This process iteratively refines the image, removing noise until a clean reconstruction is obtained at t=1. The shifting patch locations during each iteration help to avoid boundary artifacts in the final image.
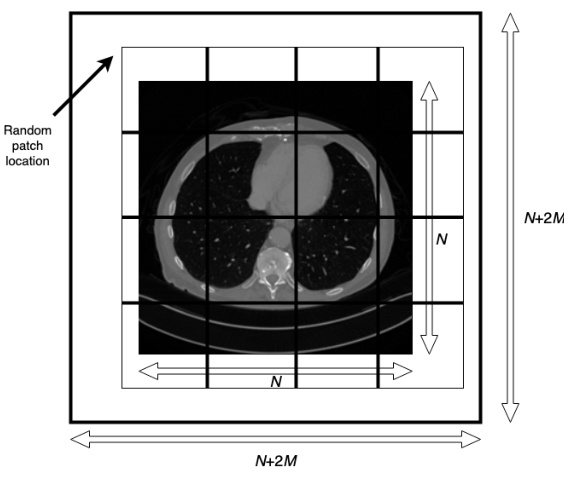
The figure illustrates the process of preparing an image for patch-based processing. First, the image is zero-padded on all sides by M pixels. Then, this padded image is partitioned into (k+1)² patches, each of size P x P. The patches are arranged in a grid, where k = [N/P] and N is the original image size. The central N x N area of the padded image corresponds to the original image. This method provides a way to obtain overlapping patches without explicitly using overlapping patches, which would lead to boundary artifacts.
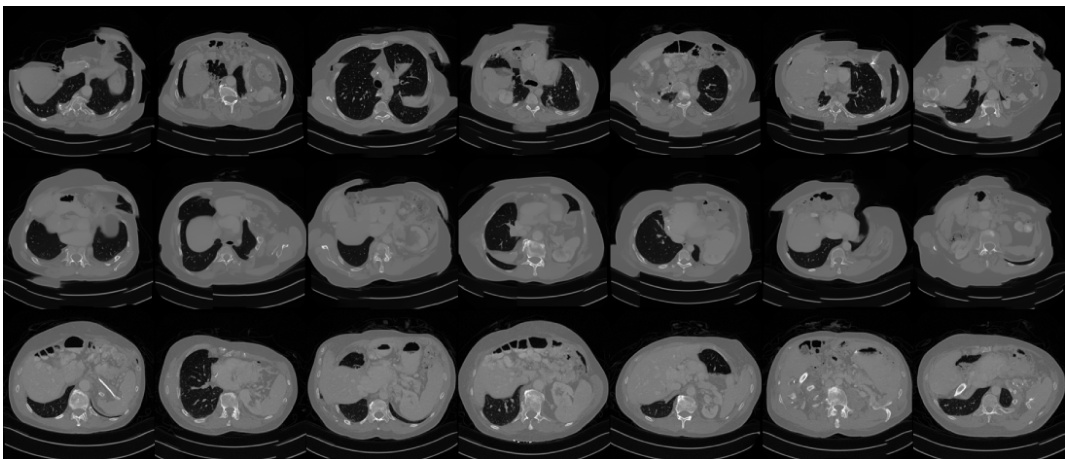
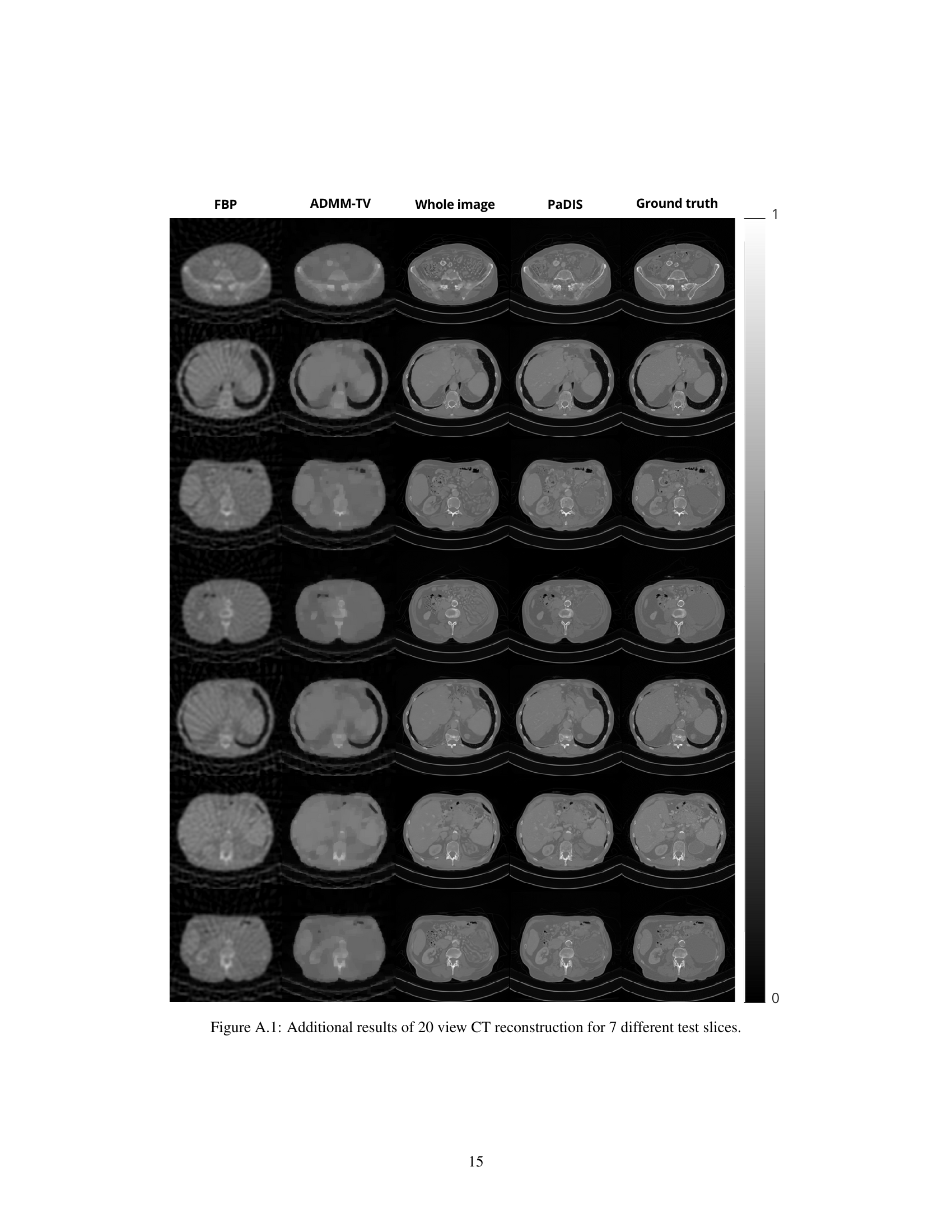
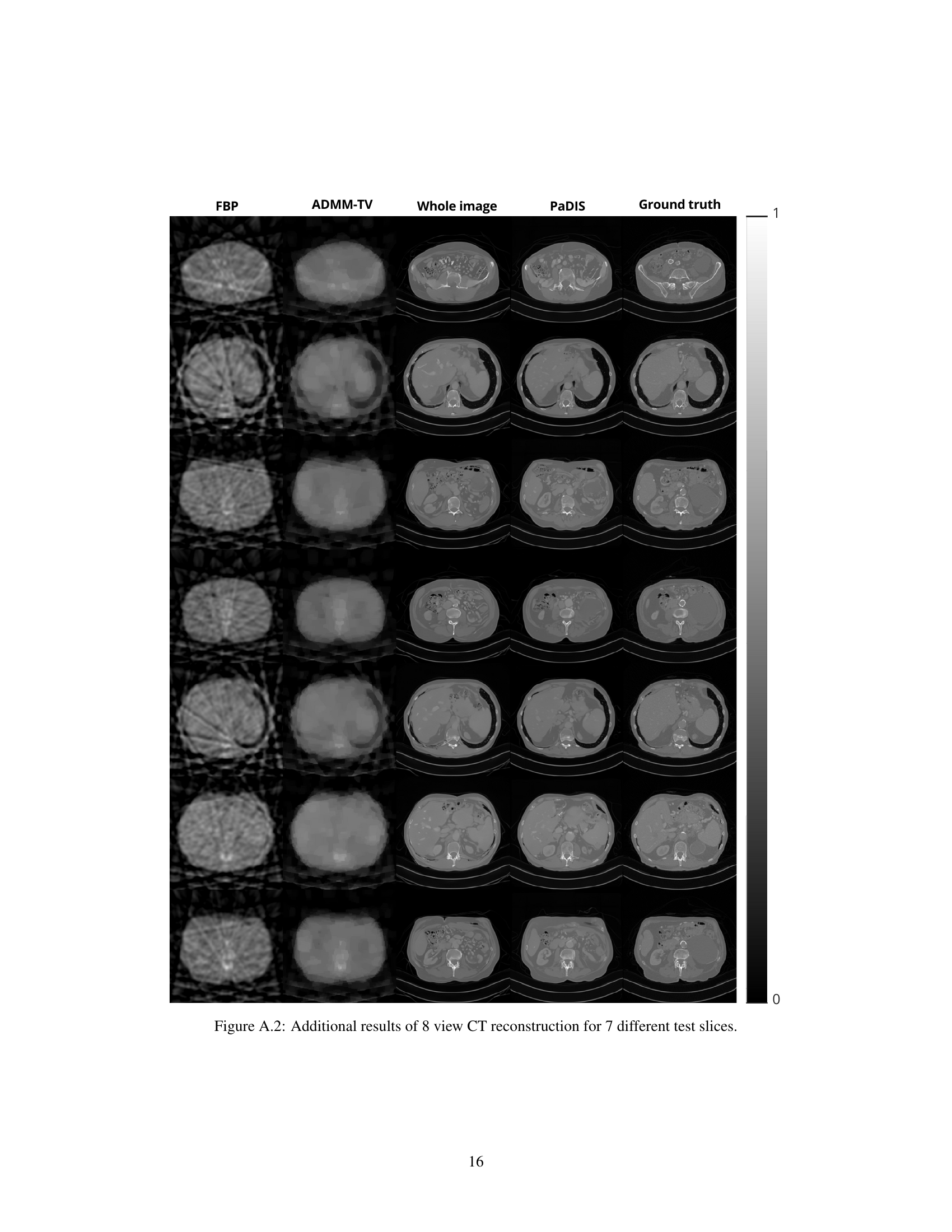
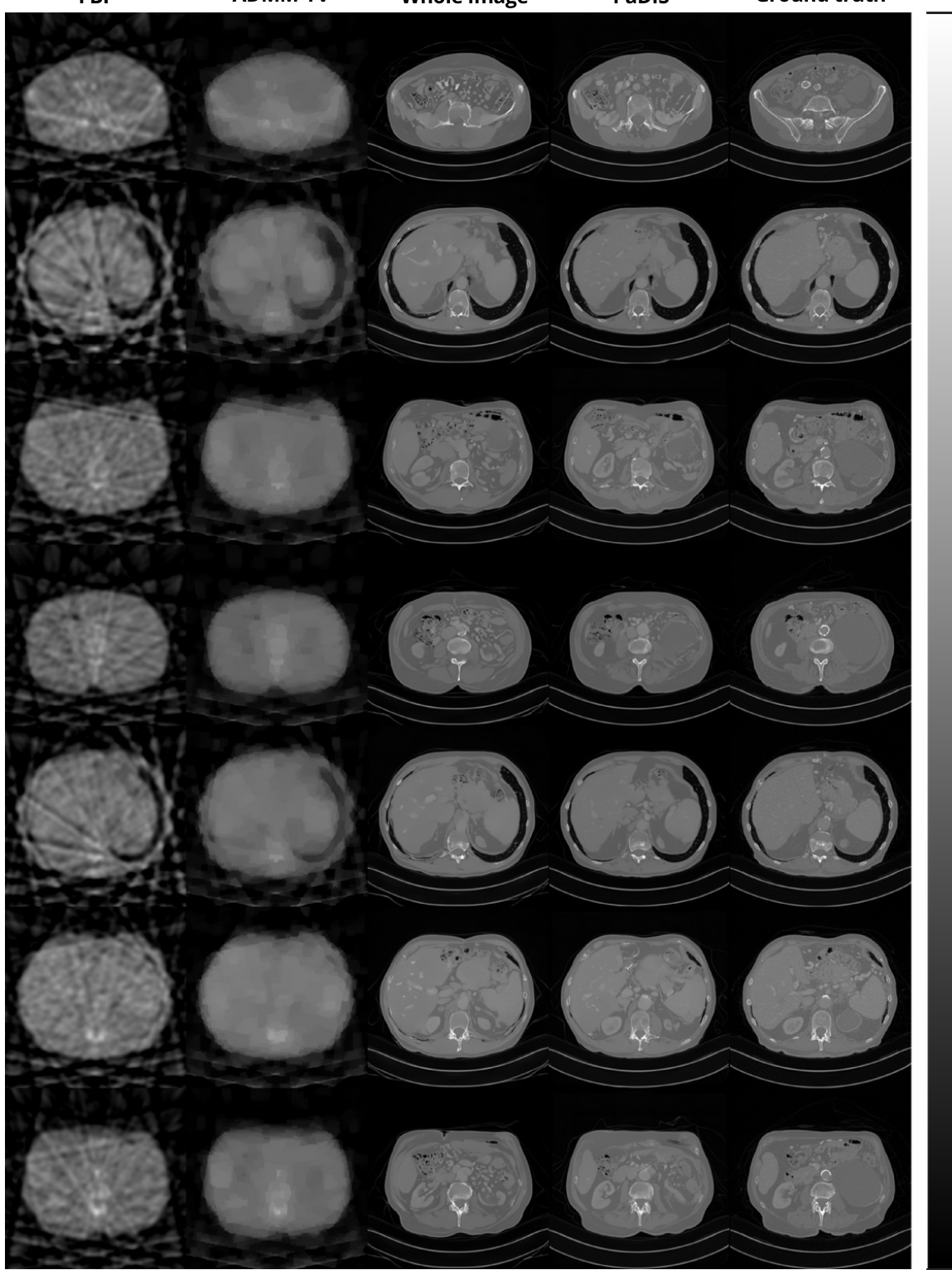
This figure displays additional results of 20-view CT reconstruction for seven different test slices. It showcases the performance of several methods, including Filtered Back Projection (FBP), ADMM-TV, a whole image diffusion model, and the proposed PaDIS method. Each column shows the reconstruction results for a specific slice, allowing for a visual comparison of the different methods. The ground truth is also included for reference.
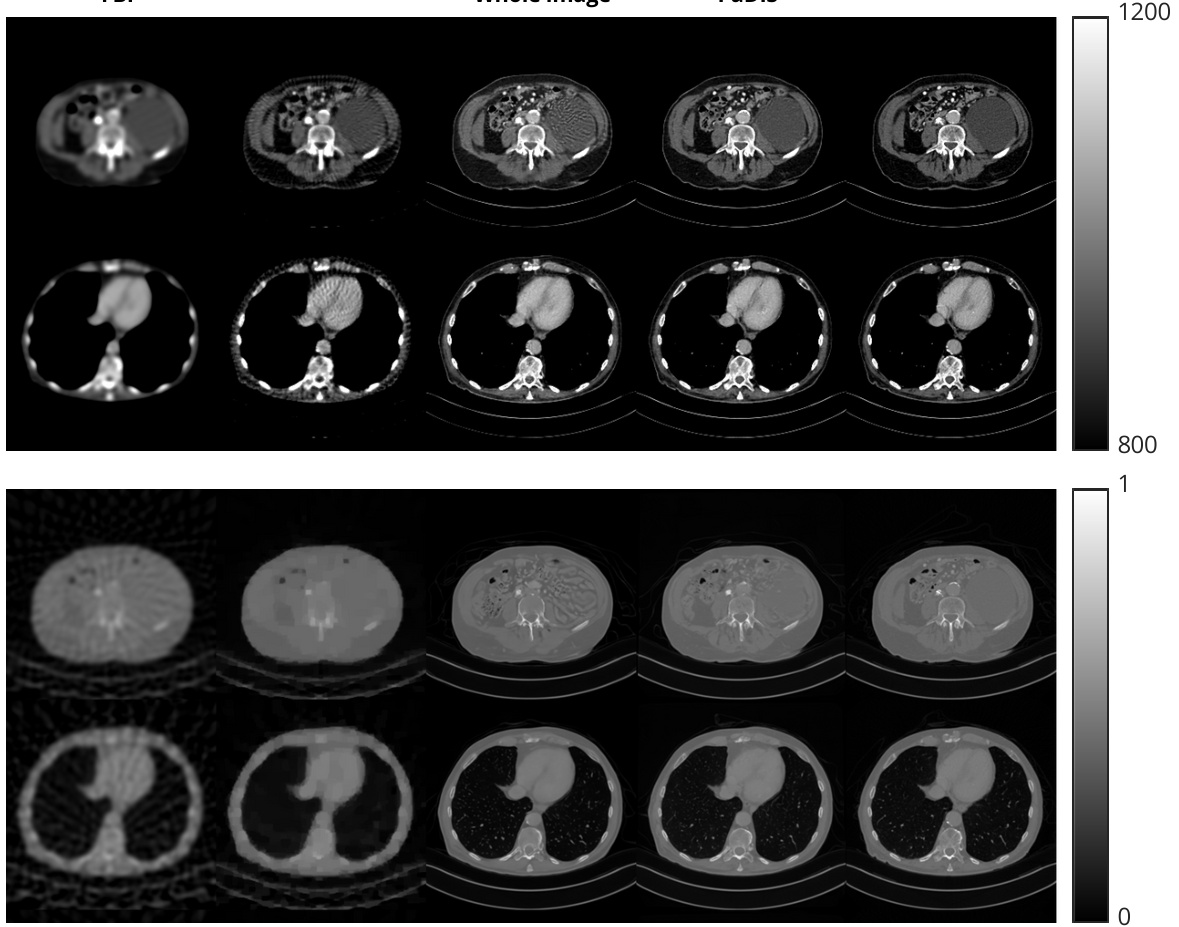
This figure demonstrates the unconditional image generation capabilities of three different methods: a whole-image diffusion model, a patch-based method from a previous work ([16]), and the proposed PaDIS method. The top row shows the results from training and generating with the entire image. The middle row shows the result of using only patches to train a model and generate individual patches, then assembling them without considering global image consistency. The bottom row shows the results of the proposed PaDIS method which addresses the shortcomings of the previous patch-based approach by incorporating positional information and cleverly combining patches to generate complete, artifact-free images.

This figure displays additional examples of image deblurring results using four different methods: Measurement (blurred image), ADMM-TV, Whole image (using a whole-image diffusion model), PaDIS (the proposed patch-based diffusion model), and Ground truth (original, unblurred image). Each row shows the results for a different image. The figure visually demonstrates the performance comparison of different methods in deblurring images corrupted with Gaussian noise.

This figure displays additional examples of image deblurring results, comparing the performance of ADMM-TV, the whole-image diffusion model, and the proposed PaDIS method. Each row shows a different image, with the ‘Measurement’ column showing the blurry image, followed by the results from ADMM-TV, whole image diffusion, PaDIS, and finally the ‘Ground truth’ column showing the original, unblurred image. The results demonstrate the visual quality and effectiveness of the PaDIS method in reducing noise and restoring the sharpness and details of the images.

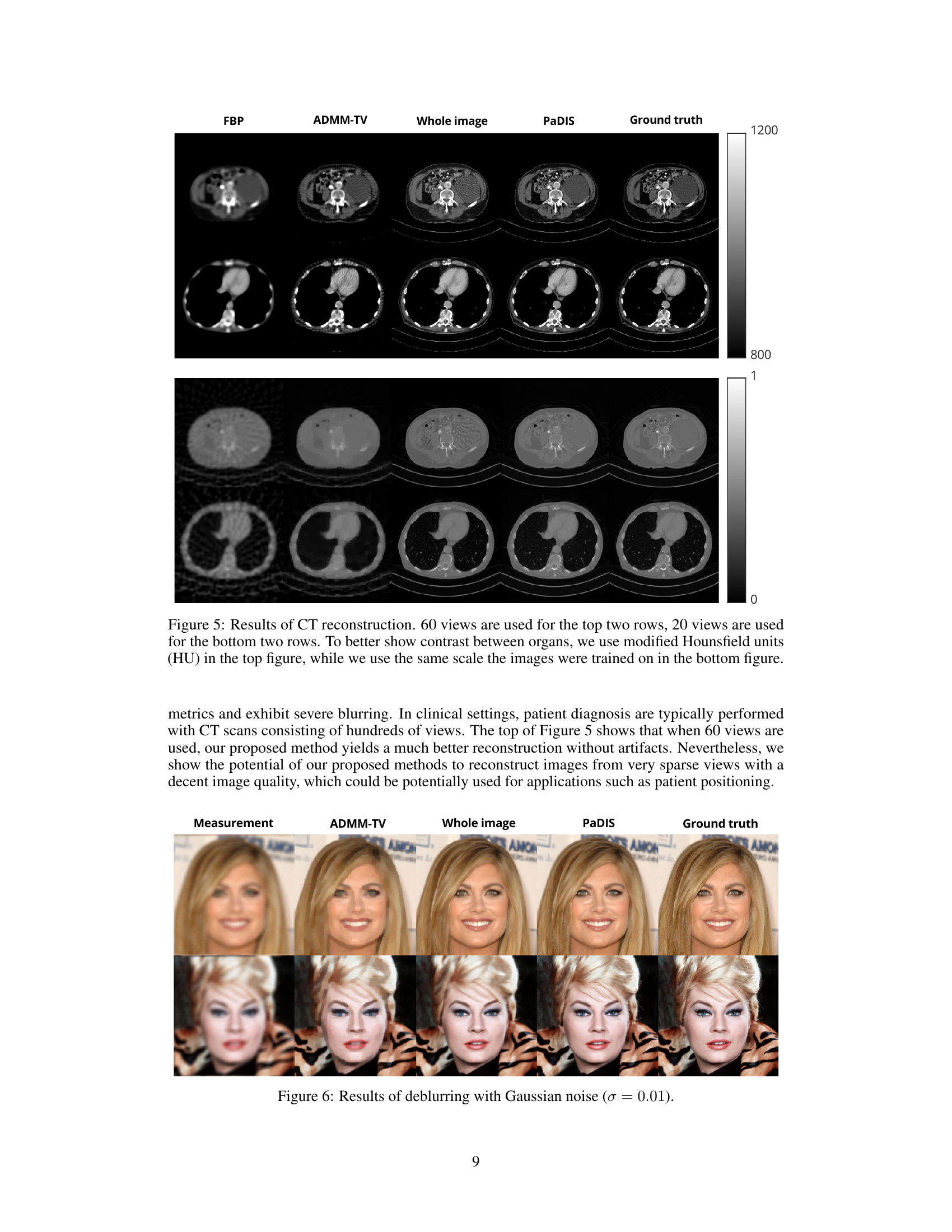
This figure compares the results of CT reconstruction using different methods: Filtered Back Projection (FBP), ADMM-TV, a whole image diffusion model, and the proposed PaDIS method. Two different scenarios are shown: one with 60 projection views and another with 20. The top row uses a modified Hounsfield unit scale to better visualize organ contrast, while the bottom row uses the same scale as the training data. The results demonstrate the improved performance of PaDIS, especially in the low-view scenario, compared to traditional and other diffusion methods.
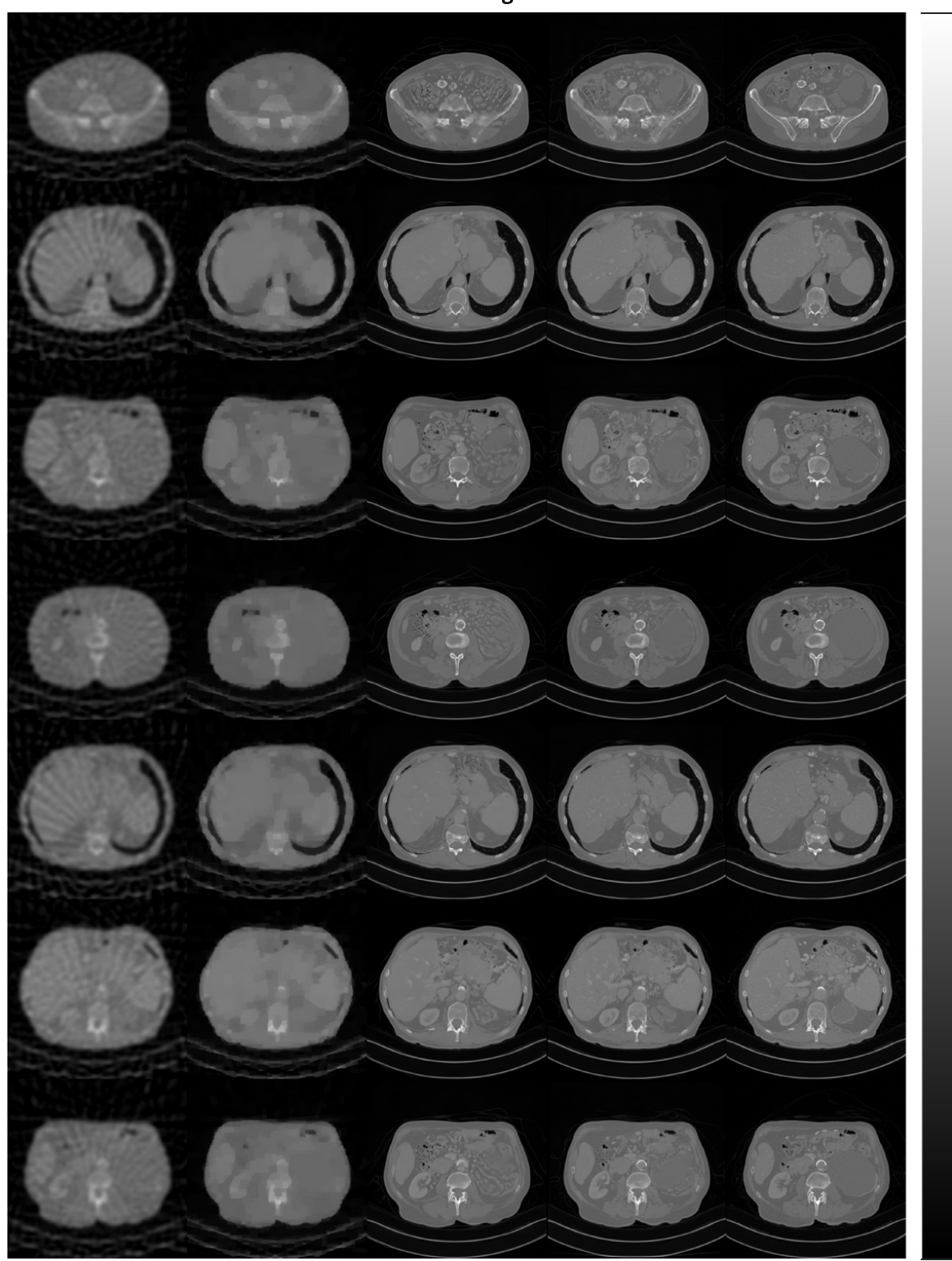
This figure shows additional results of 20-view CT reconstruction for seven different test slices. It expands on the results presented in the main body of the paper, providing visual examples to supplement the quantitative data.
This figure shows additional results of 20-view CT reconstruction for 7 different test slices. It compares the results of five methods: FBP, ADMM-TV, the whole image diffusion model, the proposed PaDIS method, and the ground truth. The images are arranged in columns, with each column representing one of the methods. Each row presents a slice from a different test image. The figure illustrates the performance of the proposed PaDIS method in reconstructing CT images from sparse data, and shows the qualitative difference between the proposed method and other traditional or deep learning based methods.

This figure shows additional visual results of the deblurring experiments with Gaussian noise (σ = 0.01). It presents a comparison between the results obtained using ADMM-TV, the whole image diffusion model, the PaDIS method, and the ground truth images for several different faces. The results show how well each method is able to recover the sharp details and clean textures of the images after they’ve been blurred and corrupted by noise.

This figure shows additional examples of the deblurring results. The images in each row show the results for a particular test image. The columns show (from left to right): the blurry input image, the deblurred images generated using ADMM-TV, the whole image diffusion model, PaDIS, and the ground truth image.
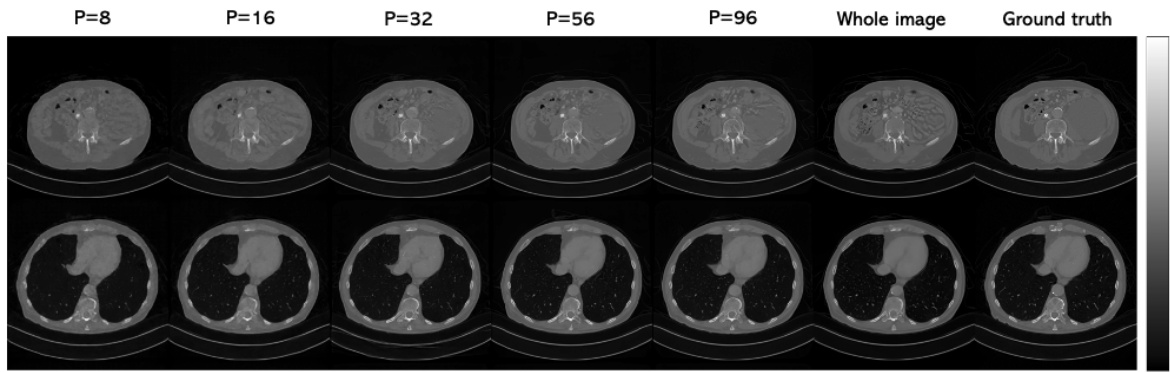
This figure demonstrates the effect of using different patch sizes (P) during the reconstruction process using the PaDIS method for 20-view CT reconstruction. It shows that the quality of the reconstruction varies depending on the size of the patches used. Small patch sizes lead to artifacts such as blurry features or the appearance of false features, while larger patches tend to produce better results. The figure visually compares the results obtained using patch sizes of 8, 16, 32, 56, and 96, alongside the result from using the whole image as a single patch (256). The ground truth image is also provided for comparison.

This figure compares the results of 20-view CT reconstruction using the proposed PaDIS method and a traditional whole-image diffusion model. The images in the top row show the reconstructions obtained with the PaDIS method, while those in the bottom row show reconstructions using the whole-image method. Each column represents a reconstruction from a dataset of different sizes. The ground truth is shown in the far-right column. The figure demonstrates that, despite decreasing dataset size, the PaDIS method is able to maintain reasonably consistent image quality. The whole-image diffusion model’s image quality is considerably worse, especially in the reconstructions obtained from smaller training datasets.
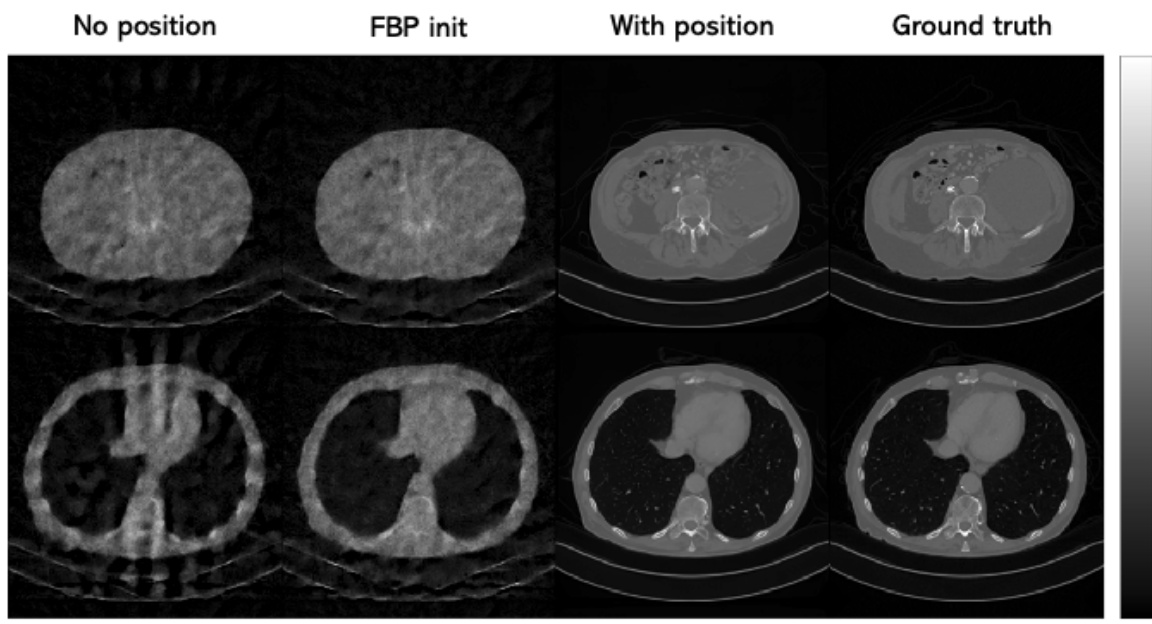
This figure demonstrates the importance of adding positional encoding information into the patch-based network. When positional information is not included, the network simply learns a mixture of all patches, resulting in a very blurry image with many artifacts. Even when a better initialization of the image is provided, the same blurriness remains. The figure shows the results for two different test images, comparing the performance with positional encoding versus without it, along with the filtered back-projection (FBP) baseline and the ground truth images.

This figure compares the results of using the proposed Patch Diffusion Inverse Solver (PaDIS) method with different sampling and inverse problem-solving algorithms against a whole-image diffusion model for 20-view CT reconstruction. The top row shows results using PaDIS, while the bottom row uses the whole-image model. The different algorithms used are: Predictor-corrector, Langevin, DDNM, and DPS. The ground truth image is also provided for comparison. The figure demonstrates the flexibility of PaDIS by showing comparable results across different sampling methods.

This figure shows additional results for 20-view CT reconstruction on 7 different test slices. It supplements the main results presented in Table 1 of the paper by providing visual examples of the reconstruction quality achieved using the proposed PaDIS method, compared against other methods (FBP, ADMM-TV, Whole image). Each row represents a different slice from the CT scan data, and each column represents a different reconstruction method. This allows a visual comparison of the effectiveness of each method in reconstructing different regions of the CT image.

This figure shows additional results of 20-view CT reconstruction for 7 different test slices. It expands on the main results presented in Table 1 of the paper, providing visual examples to complement the quantitative data. Each column represents a different reconstruction method: FBP (Filtered Back Projection), ADMM-TV (Alternating Direction Method of Multipliers with Total Variation regularization), Whole image, PaDIS (the proposed Patch Diffusion Inverse Solver), and Ground truth. The rows represent different slices from the test dataset. The image quality and detail are compared across different reconstruction methods for these seven slices.

This figure shows additional results for 20-view CT reconstruction on seven different test slices. It visually compares the results from Filtered Back Projection (FBP), ADMM-TV, the whole image diffusion model, the proposed PaDIS method, and the ground truth. The purpose is to show the performance of PaDIS in more detail and across several different slices, beyond the summary statistics presented in Table 1 of the main paper.
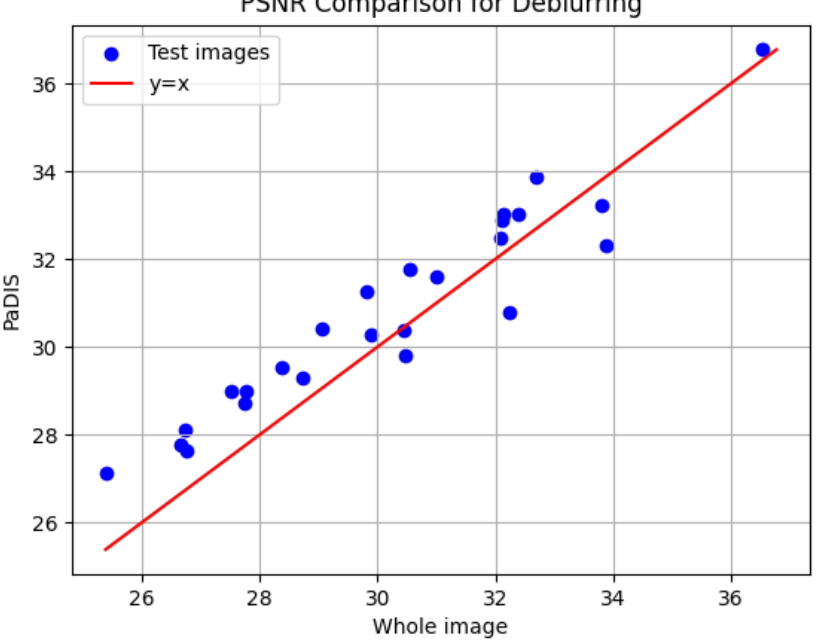
This figure shows a comparison of the Peak Signal-to-Noise Ratio (PSNR) for deblurring results obtained using two methods: a whole-image diffusion model and the proposed patch-based diffusion model. The x-axis represents the PSNR values obtained from the whole-image method for each test image, and the y-axis represents the corresponding PSNR values obtained using the proposed method. A red line representing y=x is added as a visual aid to quickly compare performance between both models on a per image basis.
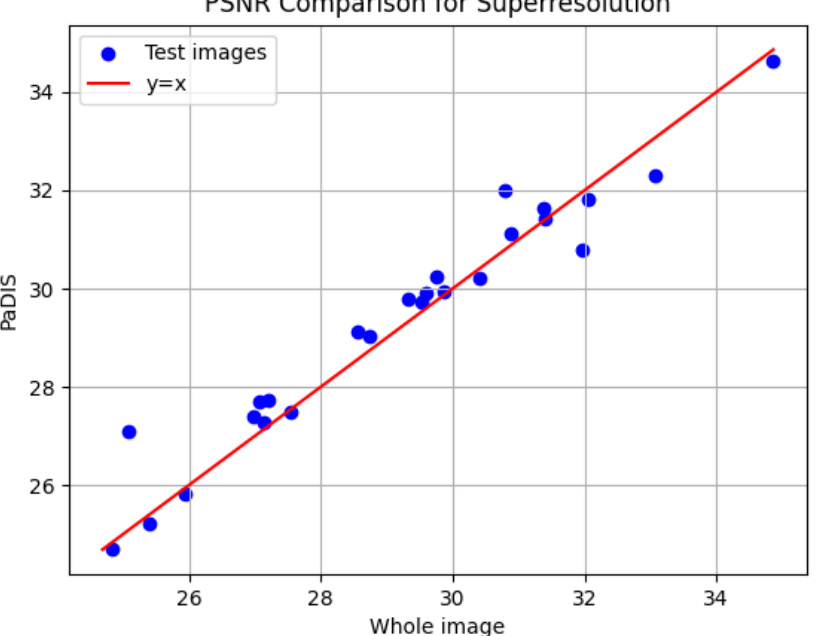
This figure compares the Peak Signal-to-Noise Ratio (PSNR) values for super-resolution between two models: a whole-image model and a proposed patch-based model. The x-axis represents the PSNR of the whole-image model, and the y-axis represents the PSNR of the proposed method. Each point represents the PSNR for a single image in the test dataset. The red line shows the y=x line, indicating where the PSNR values for both models are equal. Points above the line indicate that the proposed model outperforms the whole-image model for that particular image, while points below indicate the opposite.
More on tables

This table compares the performance of different methods on three inverse problems: CT reconstruction with 20 and 8 views, image deblurring, and image super-resolution. The methods compared include baselines (FBP, ADMM-TV, PnP-ADMM, PnP-RED), a whole-image diffusion model, several sampling algorithms used with the whole-image diffusion model (Langevin dynamics, predictor-corrector, VE-DDNM), other patch-based methods (Patch Averaging, Patch Stitching), and the proposed PaDIS method. The evaluation metrics are PSNR and SSIM, averaged across all test images. Bold values indicate the best performing method for each task.
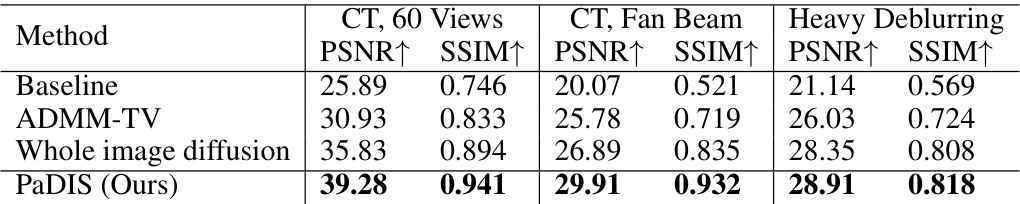
This table presents the quantitative results of additional experiments conducted on three different inverse problems: 60 view CT reconstruction, fan beam reconstruction using 180 views, and deblurring with a 17x17 uniform kernel. Each problem’s results are shown as PSNR and SSIM values, averaged across all images in the test dataset, comparing the proposed PaDIS method with baseline results, ADMM-TV, and a whole image diffusion model. The best-performing method for each metric is highlighted in bold.

This table shows the effect of different patch sizes (P) used during reconstruction on the performance of the proposed PaDIS method for the 20-view CT reconstruction task. The results (PSNR and SSIM) demonstrate that choosing an appropriate patch size is crucial for optimal performance. Smaller patch sizes may struggle to capture global image information while very large patch sizes may require more memory and training data, resulting in suboptimal performance. The best performance is achieved with a patch size of 56.

This table shows the impact of varying training dataset sizes on the performance of both the proposed patch-based method and the traditional whole-image diffusion model in 20-view CT reconstruction. The results demonstrate that while both approaches show a decrease in performance (measured by PSNR and SSIM) with reduced dataset size, the whole-image model’s performance degrades more significantly than the proposed patch-based method, highlighting the latter’s improved data efficiency.
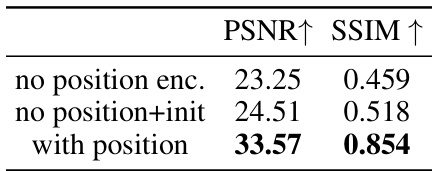
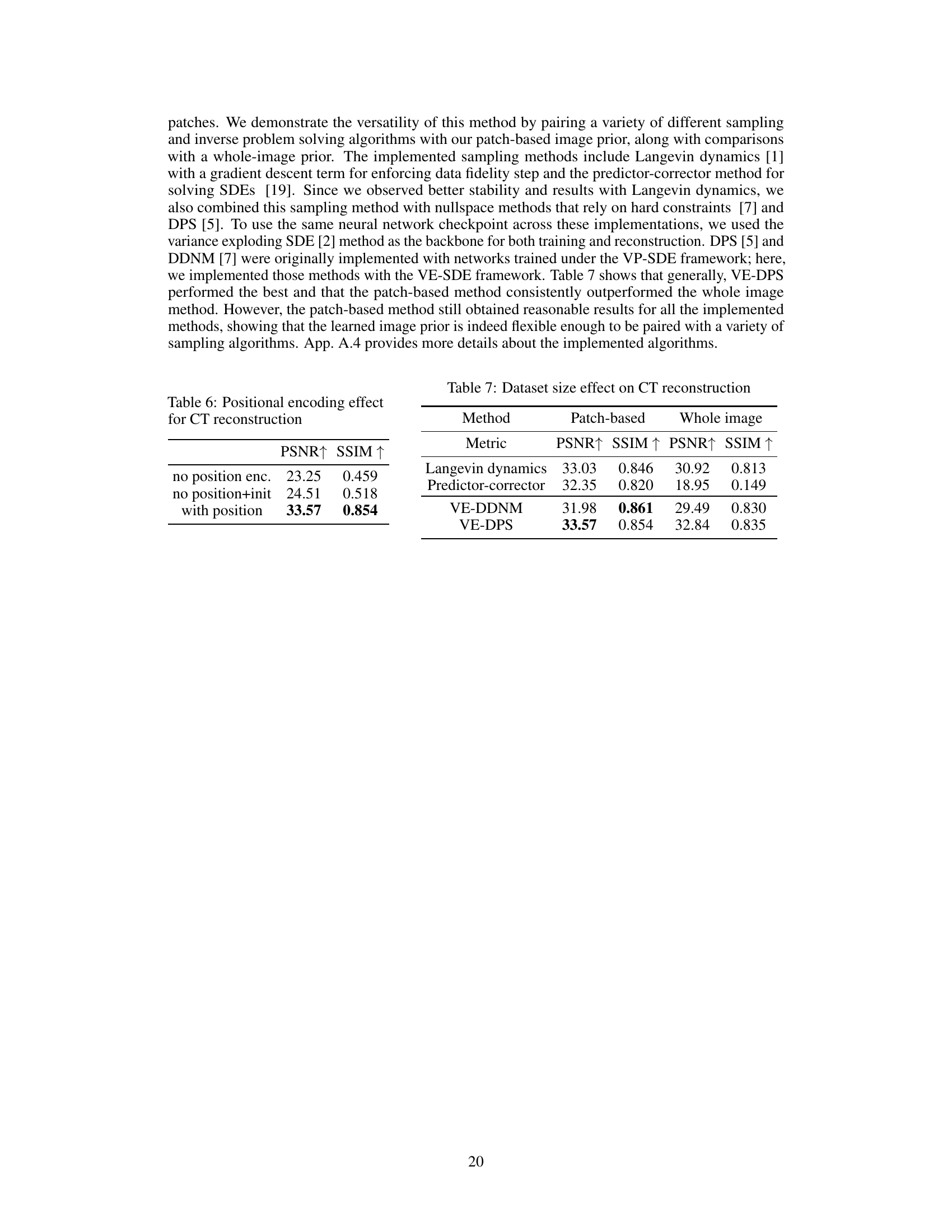
This table presents the results of an ablation study on the effect of positional encoding in the proposed PaDIS method for CT reconstruction. Three experimental settings are compared: (1) no positional encoding; (2) no positional encoding but with initialization; and (3) with positional encoding. The results show a significant improvement in PSNR and SSIM when positional encoding is included, highlighting its importance for effective image reconstruction in this context.

This table compares the performance of different sampling methods (Langevin dynamics, predictor-corrector, VE-DDNM, VE-DPS) for CT reconstruction using both patch-based and whole-image diffusion models. The results show the PSNR and SSIM metrics for each method and model type. It highlights the impact of dataset size on reconstruction accuracy for each approach.

This table compares the performance of different methods on three inverse problems: CT reconstruction (with 8 and 20 views), image deblurring, and image super-resolution. The methods compared include baselines (FBP, ADMM-TV, PnP-ADMM, PnP-RED), a whole-image diffusion model, and the proposed PaDIS method along with several sampling algorithms. The table reports the Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index (SSIM) metrics, which are higher is better. The best performing method for each task is shown in bold.

This table presents a comparison of Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index (SSIM) for three different inverse problems (CT reconstruction with 8 and 20 views, image deblurring, and image super-resolution). The results are compared across several methods: a baseline (no reconstruction), Total Variation with Alternating Direction Method of Multipliers (ADMM-TV), Plug-and-Play with ADMM (PnP-ADMM), Plug-and-Play with Regularization by Denoising (PnP-RED), a whole-image diffusion model, and several sampling methods (Langevin dynamics, predictor-corrector, Variation Exploding DDIM (VE-DDIM)) paired with the proposed PaDIS method. The best performance for each metric and problem is highlighted in bold, demonstrating the superior performance of PaDIS especially when compared to the whole-image diffusion model.

This table compares the performance of different methods for solving three inverse problems: CT reconstruction (with 8 and 20 views), image deblurring, and image super-resolution. The methods compared include baselines (FBP, ADMM-TV), plug-and-play methods (PnP-ADMM, PnP-RED), a whole-image diffusion model, and other sampling methods applied to the whole image diffusion model (Langevin dynamics, predictor-corrector, VE-DDNM). The proposed PaDIS method is also included. The results are presented in terms of average PSNR and SSIM across the test images. Bold values highlight the best performing methods for each problem.

This table presents a comparison of Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index (SSIM) for three different inverse problems (CT reconstruction with 20 and 8 views, image deblurring, and image super-resolution). It compares the performance of several methods: a baseline (no reconstruction), ADMM-TV, PnP-ADMM, PnP-RED, a whole image diffusion model, Langevin dynamics, predictor-corrector, VE-DDNM, patch averaging, patch stitching, and the proposed PaDIS method. The best results for each metric in each category are highlighted in bold. The results demonstrate the proposed PaDIS model’s performance compared to other methods across various inverse problems.
Full paper#