↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Estimating accurate signed distance functions (SDFs) from point clouds is crucial in various applications, but existing methods struggle with noisy data or slow convergence. Data-driven methods are fast but generalize poorly, while overfitting-based methods are slow. The problem is exacerbated in challenging scenarios like highly noisy point clouds.
This paper introduces LocalN2NM, a method that leverages the strengths of both data-driven and overfitting-based approaches. It uses a novel statistical reasoning algorithm to finetune data-driven priors without needing clean data or point normals. This leads to faster convergence and better generalization compared to existing methods. LocalN2NM demonstrates superior performance in surface reconstruction and point cloud denoising across multiple benchmark datasets.
Key Takeaways#
Why does it matter?#
This paper is highly relevant to researchers working on 3D surface reconstruction and point cloud processing. It offers a novel approach that combines the strengths of data-driven and overfitting-based methods, resulting in faster inference, better generalization, and higher accuracy. This work has the potential to advance various applications including computer graphics, computer vision, and robotics. By introducing a novel loss function and a statistical reasoning algorithm in local regions, this work opens new avenues for improving the accuracy and efficiency of neural SDF inference from noisy point clouds.
Visual Insights#
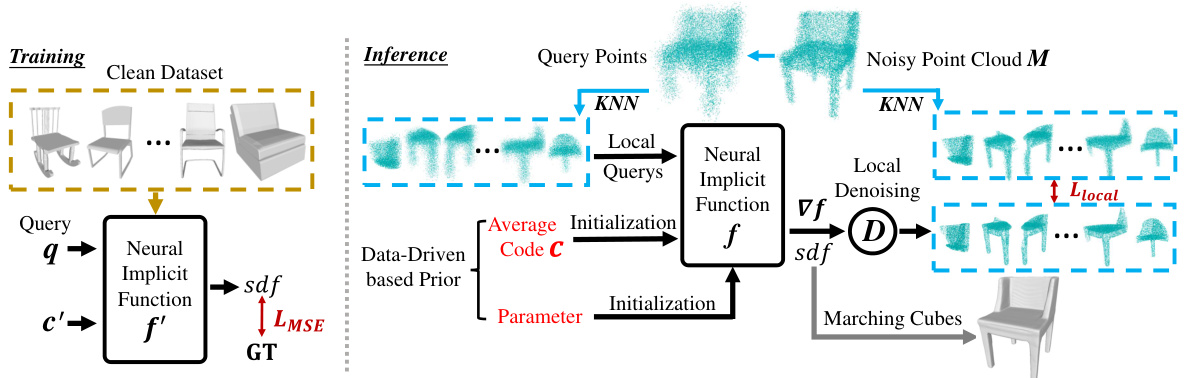
This figure illustrates the proposed method’s two-stage process: (1) training a data-driven prior using a clean dataset to learn a neural implicit function, and (2) inference on a noisy point cloud, where the learned prior is fine-tuned using a novel statistical reasoning algorithm to infer a neural SDF without needing signed distance supervision, clean points, or point normals. The diagram shows the flow of data and the key components, including KNN, local queries, local denoising, and marching cubes for surface reconstruction.

This table presents a numerical comparison of the proposed method with several state-of-the-art methods on the ShapeNet dataset. The comparison uses three metrics: CDL1 (Chamfer Distance L1) which measures the distance between the reconstructed surface and the ground truth, NC (Normal Consistency) which measures the accuracy of the normals, and F-Score which is a combined metric reflecting surface reconstruction quality. Lower values of CDL1 and higher values of NC and F-Score indicate better performance.
In-depth insights#
Prior-Finetuning#
Prior-finetuning, in the context of neural signed distance function (SDF) inference, presents a powerful strategy to leverage the strengths of both data-driven and overfitting-based approaches. Data-driven priors provide a strong initialization, accelerating convergence and improving generalization compared to purely overfitting methods that start from scratch. Finetuning adapts this prior to a specific, noisy point cloud, allowing the model to capture fine details and overcome the limitations of limited training data, thus addressing the poor generalization often associated with purely data-driven methods. This approach cleverly combines the benefits of rapid inference inherent in using pretrained models with the ability to refine the reconstruction for a single, noisy input, achieving superior accuracy. A key challenge lies in the design of the finetuning loss function: it must be robust to noise, require minimal supervision, and effectively guide the network toward an accurate SDF representation. The success of prior-finetuning hinges on carefully selecting a suitable prior model and loss function to achieve this balance. The overall effect is a significant improvement in both the speed and accuracy of neural SDF inference, leading to improved 3D surface reconstruction and point cloud denoising.
Noise-Robust SDF#
The concept of a ‘Noise-Robust SDF’ is crucial for real-world applications of Signed Distance Functions (SDFs). Real-world point cloud data is inherently noisy, stemming from various sources like sensor limitations and environmental factors. A noise-robust SDF method must effectively handle this noise, avoiding overfitting to spurious data points and ensuring the generated implicit surface accurately represents the underlying shape. This robustness can be achieved through several strategies, including statistical reasoning in local regions, data-driven priors (pre-trained models that capture general shape characteristics), and regularization techniques that prevent the model from becoming overly complex. The success of a noise-robust SDF approach hinges on the balance between accurately capturing details from clean data points while mitigating the impact of noise. Algorithms that incorporate robust loss functions and local filtering mechanisms are likely to prove more effective in this challenge. The ultimate goal is to produce a smooth, accurate SDF representation even from extremely noisy input data, making SDFs practical for applications such as 3D reconstruction and point cloud denoising.
Local Statistical Reasoning#
The proposed “Local Statistical Reasoning” method presents a novel approach to inferring neural signed distance functions (NDSFs) from noisy point clouds. Unlike global methods that consider the entire point cloud simultaneously, this technique focuses on smaller, localized regions. This localized approach is crucial for handling noise effectively, as it prevents noise in one area from significantly affecting the estimation of distances in other regions. The method leverages statistical reasoning within these local neighborhoods to estimate a mean zero-level set representing the underlying surface. This is achieved by minimizing the distance between sampled query points projected onto the zero-level set and the noisy points within the local region. The core innovation lies in its ability to finetune a pre-trained data-driven prior, achieving faster convergence and better generalization compared to purely overfitting-based methods. This hybrid approach combines the strengths of both data-driven priors (fast inference) and overfitting (good generalization) to produce NDSFs with higher accuracy and improved efficiency, particularly in challenging scenarios like highly noisy point clouds. The effectiveness is demonstrated by superior results on surface reconstruction and point cloud denoising benchmarks. Key advantages include the lack of reliance on clean data, point normals or signed distance supervision during inference, making it robust and widely applicable.
Efficiency Improvements#
In the realm of neural signed distance function (SDF) inference, efficiency is paramount. The presented method leverages data-driven priors finetuned through an overfitting strategy on noisy point clouds. This approach elegantly balances the strengths of both data-driven and overfitting methods. Data-driven priors provide a strong initialization, accelerating convergence and improving generalization on unseen data. The novel statistical reasoning algorithm used for finetuning significantly reduces inference time compared to purely overfitting-based methods. The local nature of this statistical reasoning further enhances computational efficiency by focusing on smaller regions of the point cloud instead of performing global operations. This combination of well-initialized priors and localized processing contributes to the overall efficiency improvements. The method’s effectiveness is demonstrated through superior results on various benchmarks, showcasing a significant speed-up in both surface reconstruction and point cloud denoising tasks while retaining or surpassing the accuracy of existing state-of-the-art techniques.
Limitations & Future Work#
This research demonstrates a novel method for inferring neural signed distance functions (NDFs) from single, noisy point clouds. A key limitation is the method’s sensitivity to extremely noisy data; while it outperforms existing methods on moderately noisy data, severely corrupted point clouds still pose challenges. Future work could focus on improving robustness to extreme noise levels, perhaps by incorporating more sophisticated noise filtering techniques or developing more robust loss functions. Another area for improvement is scalability. Although the method is faster than some overfitting-based approaches, further optimizations could make it more suitable for large-scale datasets. Exploring different architectural choices for the neural network or investigating more efficient training strategies might yield significant improvements. Finally, generalization to unseen point cloud distributions warrants further investigation; additional experiments across diverse datasets could validate the method’s broader applicability and reveal any limitations in generalization capability.
More visual insights#
More on figures
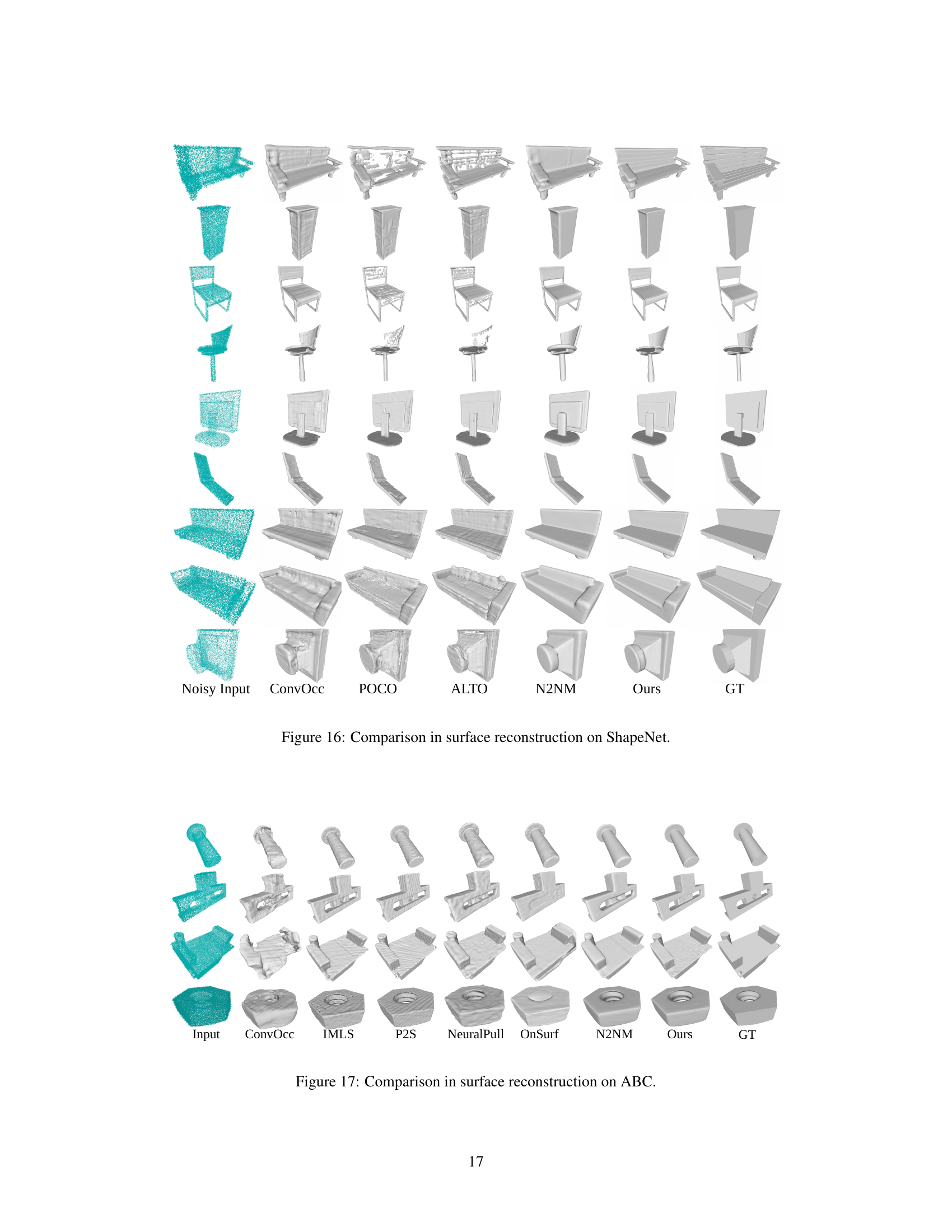
This figure displays a comparison of surface reconstruction results on the ShapeNet dataset. It shows the results of several methods, including the proposed method, alongside the ground truth. Each row represents a different shape, and the columns compare the reconstruction quality from different techniques. The noisy input is shown as the teal colored point cloud for each shape. The goal is to visualize how well each method handles noisy input data when attempting to reconstruct the underlying surface of a shape.

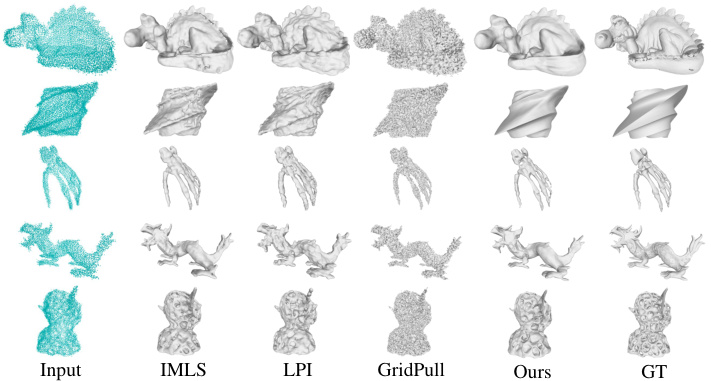
This figure compares the surface reconstruction results of different methods on the ABC dataset. The input is a noisy point cloud. The methods compared include IMLS, P2S, NeuralPull, and the proposed method (Ours). The ground truth (GT) surface is also shown for comparison. The visualization highlights the effectiveness of the proposed method in recovering detailed geometric features from noisy point cloud data, showcasing superior surface reconstruction quality compared to the baselines.
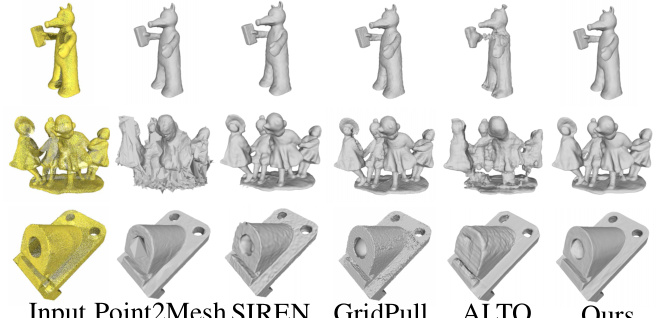
This figure compares the surface reconstruction results of several methods (Input Point2Mesh, PSR, SIREN, GridPull, ALTO, N2NM, Ours) with the ground truth (GT) on the SRB (Surface Reconstruction Benchmark) dataset. Each row shows the reconstructions for a different shape in the dataset, illustrating the relative performance of each method in terms of detail, accuracy, and noise reduction.
The figure compares the surface reconstruction results of different methods (Input, IMLS, NeuralPull, OnSurf, GridPull, N2NM, Ours, GT) on the FAMOUS dataset. Each row represents a different shape, showcasing the reconstruction capabilities of each method in terms of surface detail, smoothness, and overall accuracy. The ‘Input’ column displays the noisy point cloud used as input for each reconstruction. The ‘GT’ column shows the ground truth model. The other columns show the reconstructed surfaces from the different methods being compared.
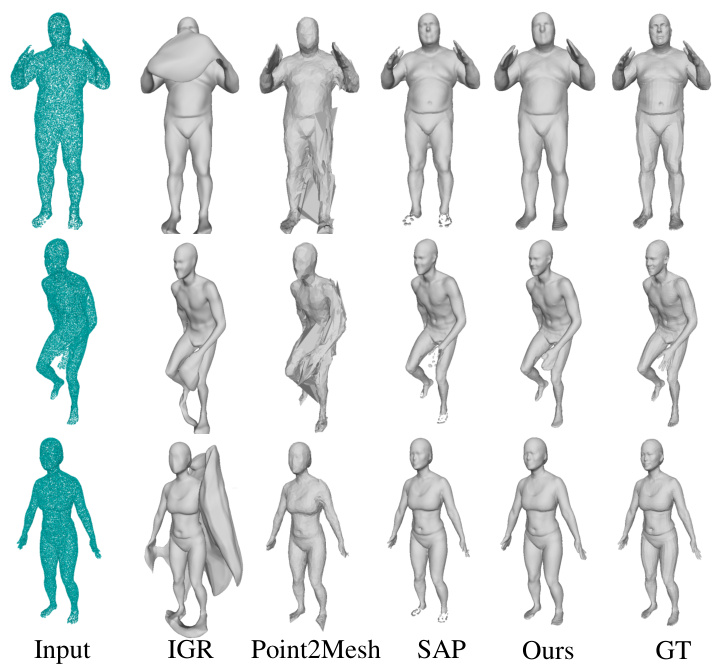
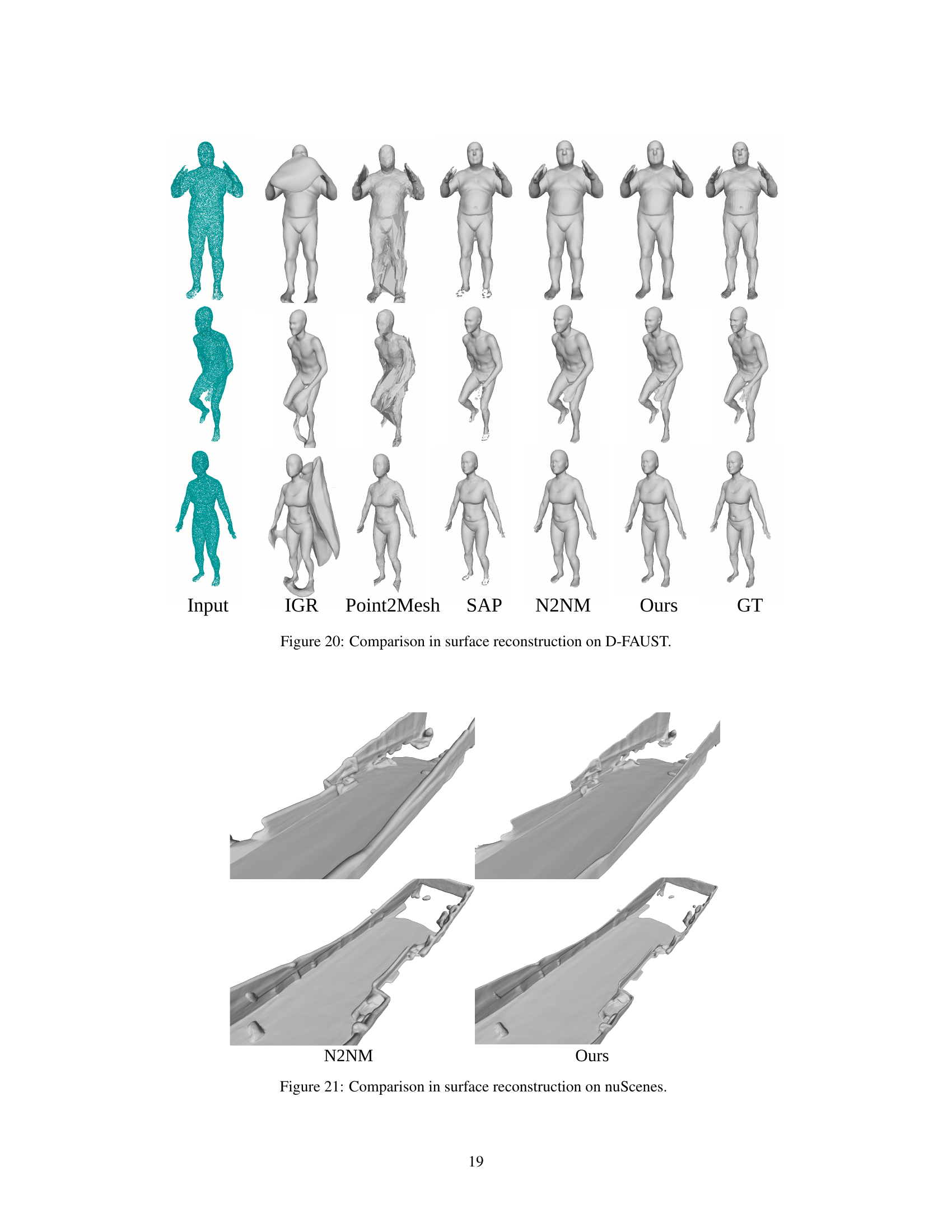
This figure compares the surface reconstruction results of several methods on the D-FAUST dataset. The D-FAUST dataset contains scans of humans in various poses. The figure shows that the proposed method (Ours) produces more accurate and complete reconstructions of the human shapes compared to other methods (IGR, Point2Mesh, SAP, N2NM). The input column shows the noisy point cloud data used for reconstruction. The GT column displays the ground truth surface for comparison.
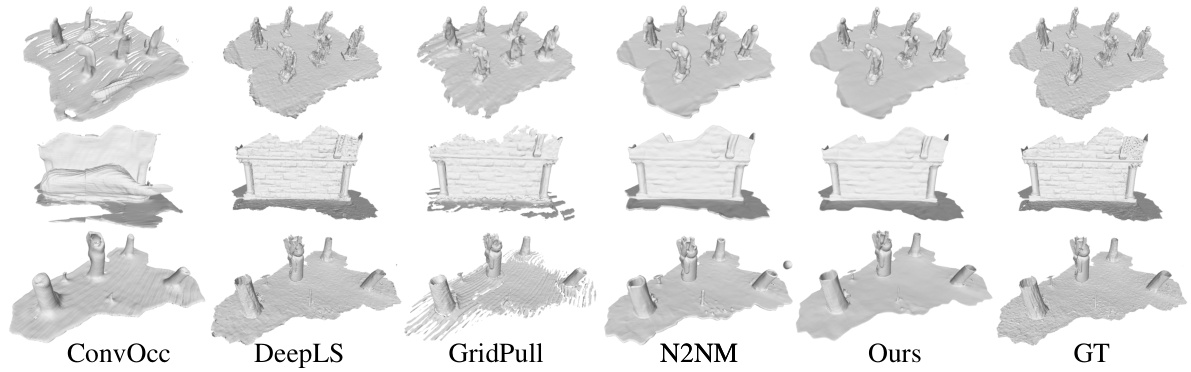
This figure compares the surface reconstruction results of several methods (ConvOcc, DeepLS, GridPull, N2NM, Ours) with the ground truth (GT) on the 3D Scene dataset. Each row shows the reconstruction of a different scene. The figure visually demonstrates the ability of the proposed method to produce more accurate and detailed surface reconstructions compared to other state-of-the-art methods, especially in handling noisy point clouds.

The figure shows a comparison of surface reconstruction results on the 3D Scene dataset. It compares the performance of the proposed method (Ours) against several other state-of-the-art methods, namely ConvOcc, DeepLS, GridPull, and N2NM. The visualization highlights the ability of the proposed method to recover finer details and complete geometry compared to other methods, especially in challenging areas with significant noise or incomplete data. The orange boxes highlight these areas of improved performance.

The figure shows a comparison of surface reconstruction results on the 3D Scene dataset using different methods: LIG, N2NM, and the proposed method. For each method, a 3D reconstruction is displayed, along with zoomed-in details showing the reconstruction quality of specific building sections. Yellow boxes highlight areas that are zoomed in.

This figure compares the surface reconstruction results obtained using different SDF initializations: random, square, sphere, and the proposed method. The results demonstrate that the proposed method significantly improves surface reconstruction accuracy and completeness compared to other initialization methods.

This figure demonstrates the robustness of the proposed method to non-uniform noise patterns. It presents visual comparisons of surface reconstruction results for three different types of nonuniform noise: patch noise, half noise, and a ground truth (GT) model. The results showcase that the proposed method handles non-uniform noise effectively, generating accurate surface reconstructions even in challenging scenarios where noise is unevenly distributed across the point cloud.

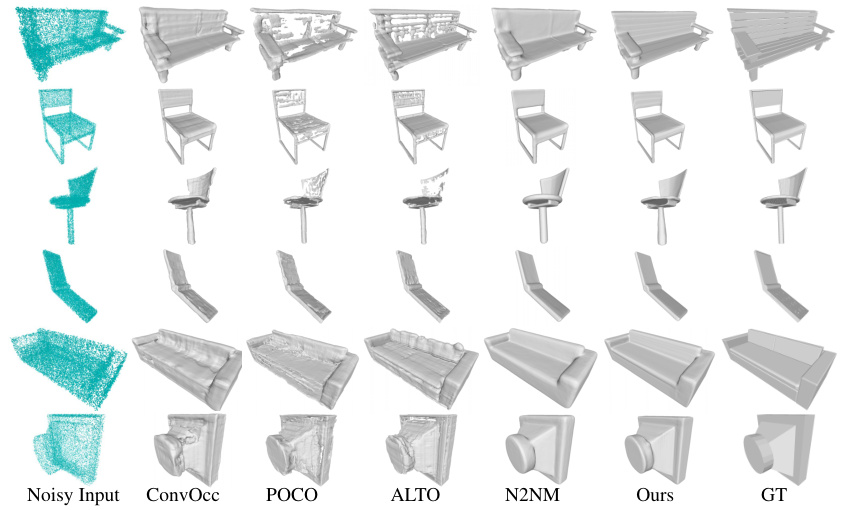
This figure shows visual comparisons of surface reconstruction results on a chair model using the proposed method under various types of noise, including impulse noise, quantization noise, Laplacian noise, and Gaussian noise. Each row represents a different type of noise. The columns show: the noisy input point cloud, the reconstruction results using four state-of-the-art methods (ConvOcc, POCO, ALTO, N2NM), the reconstruction results using the proposed method, and the ground truth model. The results demonstrate that the proposed method is effective for handling different types of noises and reconstructing accurate surface geometry.
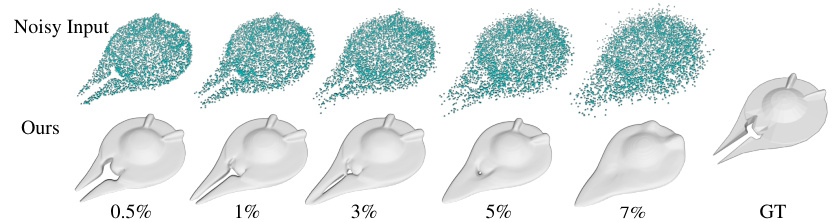
This figure shows a visual comparison of the surface reconstruction results obtained using the proposed method on a single point cloud with different noise levels. The first row displays the noisy input point clouds, while the second row shows the corresponding reconstructed surfaces generated by the proposed method. The noise levels increase from left to right, ranging from 0.5% to 7%. The last image shows the ground truth surface. This visualization highlights the robustness of the proposed method in handling various levels of noise, demonstrating its ability to reconstruct accurate surfaces even under challenging conditions.

This figure shows a visual comparison of surface reconstruction results using different numbers of points in a point cloud. The top row shows the noisy input point clouds with varying densities (10%, 30%, 50%, 70%, 100%), while the bottom row displays the corresponding reconstructed surfaces generated by the proposed method. The last image is the ground truth mesh.
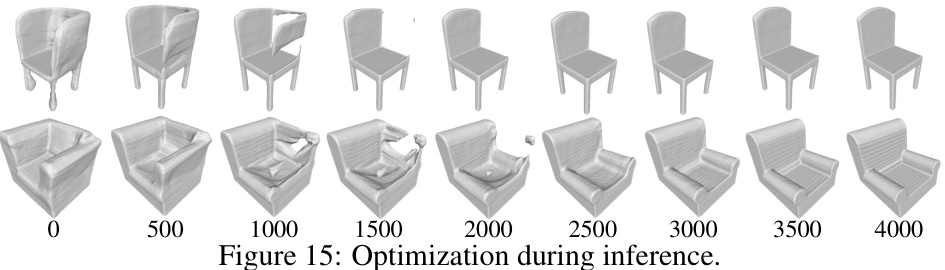
This figure shows the optimization process of the proposed method. The top row shows the reconstruction of a chair, and the bottom row shows the reconstruction of an armchair. The meshes are reconstructed using the neural SDF f learned in different iterations. The numbers below the images indicate the number of iterations. As the number of iterations increases, the shape is updated progressively to the ground truth shapes.
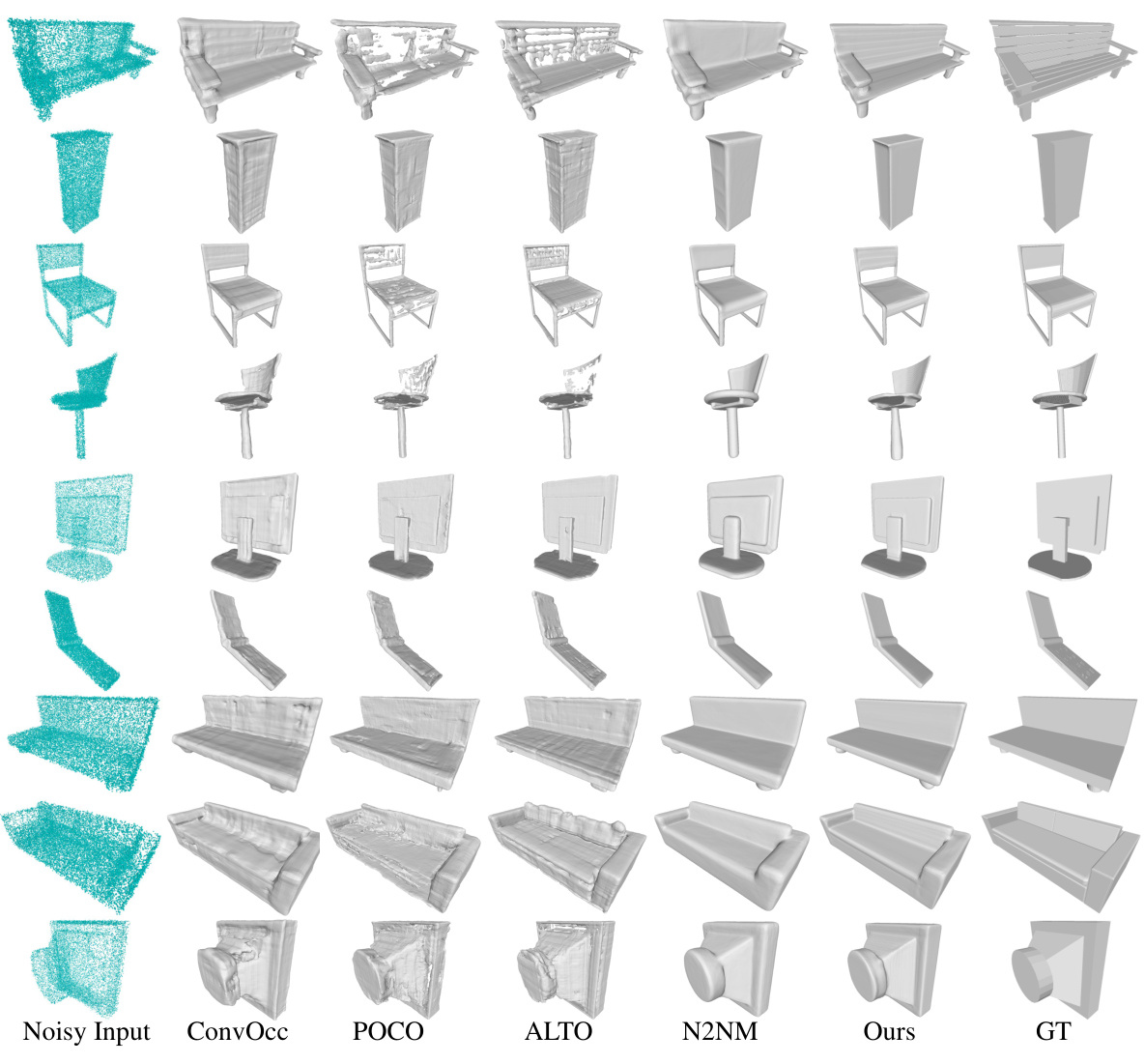
This figure compares the surface reconstruction results of several methods on the ShapeNet dataset. The first column shows the noisy input point cloud. Subsequent columns display the reconstructions generated by ConvOcc, POCO, ALTO, N2NM, and the proposed method, respectively. The final column presents the ground truth. The figure visually demonstrates the superior performance of the proposed method in accurately reconstructing surfaces compared to state-of-the-art techniques, especially in capturing finer details and handling noise.
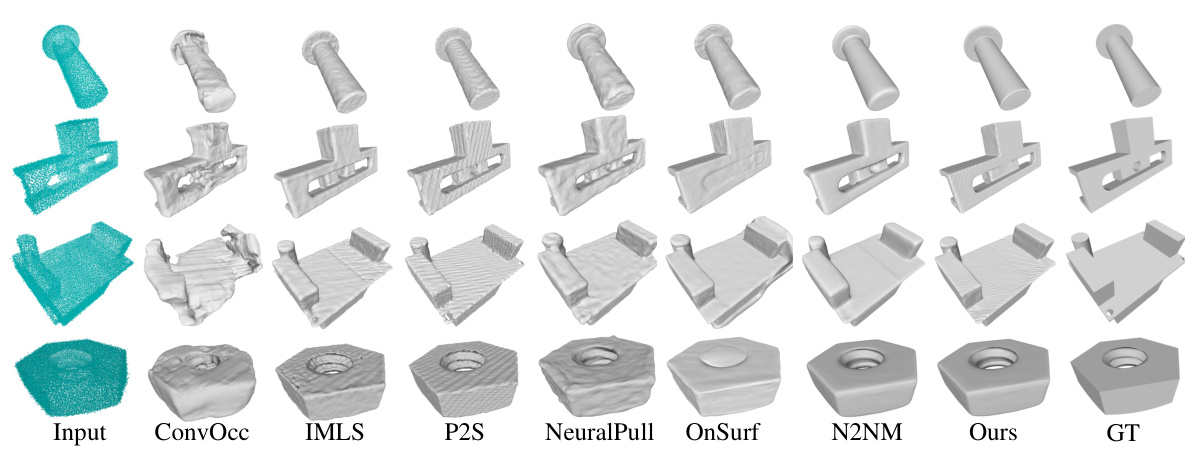
This figure compares the performance of different methods for surface reconstruction on the ABC dataset. The first column shows the noisy input point cloud. Subsequent columns display the reconstructed surfaces obtained using ConvOcc, IMLS, P2S, NeuralPull, OnSurf, N2NM, the proposed method (Ours), and the ground truth (GT). Each row represents a different shape from the dataset, demonstrating the methods’ ability to recover surface details from noisy point cloud data.

This figure compares the surface reconstruction results of different methods on the SRB dataset. It visually demonstrates the ability of each method to reconstruct 3D shapes from noisy point cloud data. The input shows the noisy point cloud data, followed by the surface reconstructions from Point2Mesh, PSR, SIREN, GridPull, ALTO, Steik, NKSR, N2NM, and the proposed method, with the ground truth reconstruction shown at the far right for comparison.
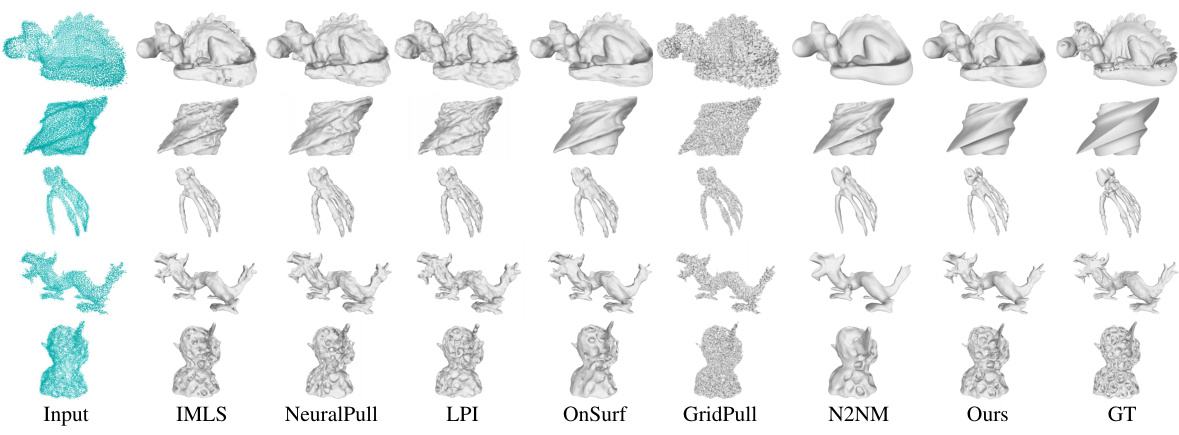
This figure compares the performance of different methods for surface reconstruction on the FAMOUS dataset. The input is a noisy point cloud. Several methods are compared, including IMLS, NeuralPull, LPI, OnSurf, GridPull, N2NM, and the proposed method. The ground truth is also shown for reference. The figure shows that the proposed method achieves better surface reconstruction results in terms of accuracy and detail compared to the other methods.
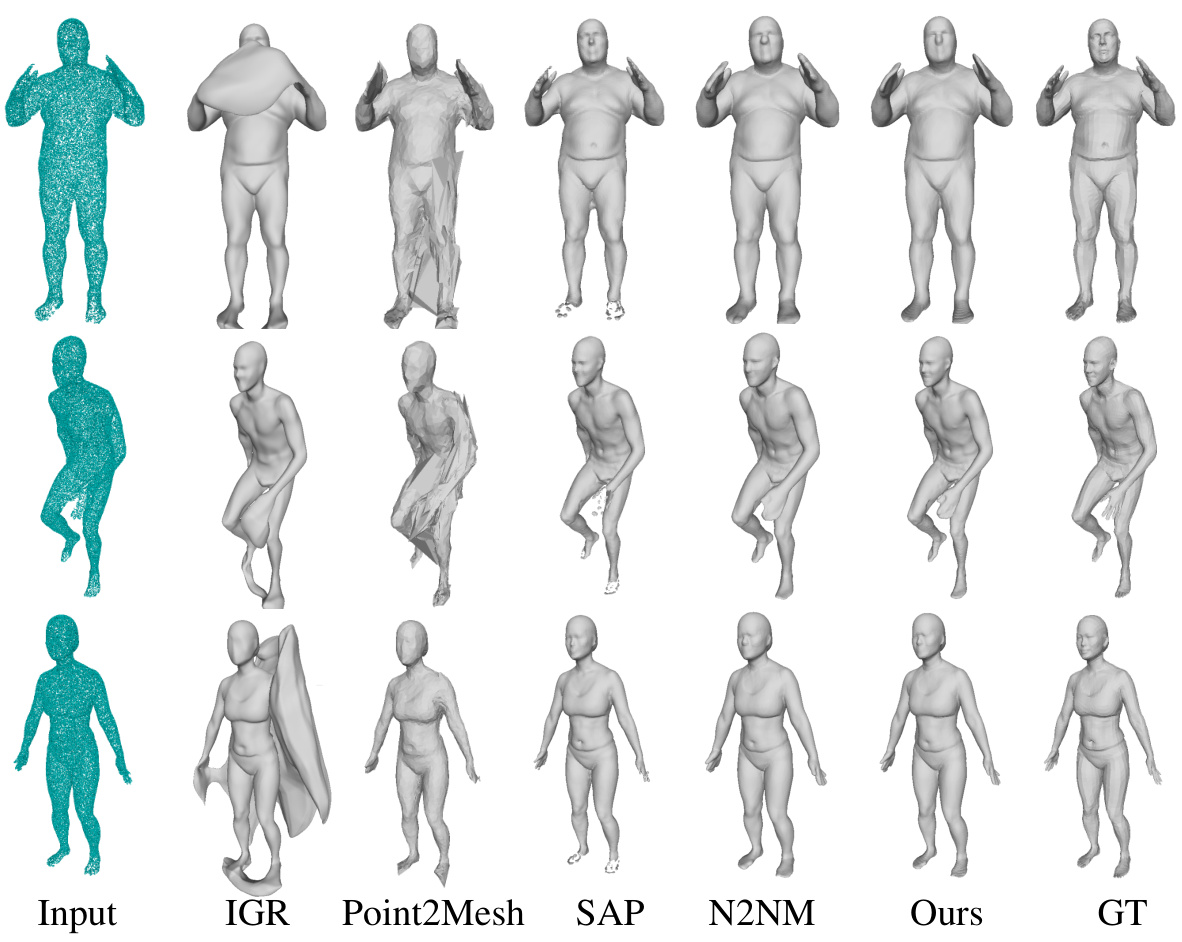
This figure compares the surface reconstruction results of different methods on the D-FAUST dataset. The D-FAUST dataset contains scans of humans in various poses. The input is a noisy point cloud of the human, and the different columns show the results of the IGR, Point2Mesh, SAP, N2NM, the proposed method, and the ground truth (GT). The figure highlights the ability of the proposed method to accurately reconstruct the fine details and poses of human shapes.
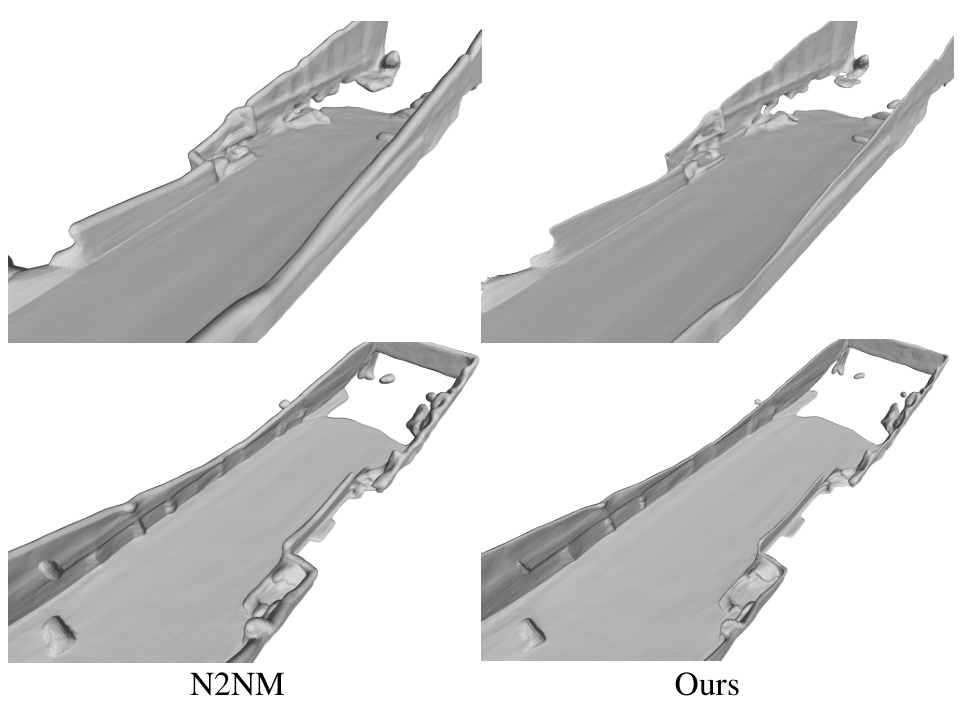
This figure compares the surface reconstruction results on the nuScenes dataset between the N2NM method and the proposed method. The image shows that the proposed method produces smoother, more complete surfaces compared to N2NM, particularly in areas with missing data or significant noise. This demonstrates the advantage of the proposed method in reconstructing surfaces from real-world, noisy point cloud data.
More on tables

This table presents a comparison of the inference time taken by three different overfitting-based methods for neural SDF inference on the ShapeNet dataset. The methods compared are SAP [70], N2NM [52], and the proposed method in the paper. The table shows that the proposed method achieves significantly faster inference (5 min) compared to the other two methods (14 min and 46 min, respectively).

This table presents a numerical comparison of the proposed method against several state-of-the-art techniques on the ABC dataset. The comparison uses the Chamfer distance (CDL2) metric, multiplied by 100, to evaluate the accuracy of surface reconstruction. Lower values indicate better performance. The results are split into two categories reflecting variations in noise level within the dataset: ABC var (variable noise) and ABC max (maximum noise). The table shows that the proposed method achieves superior performance compared to existing methods, especially under high noise conditions.
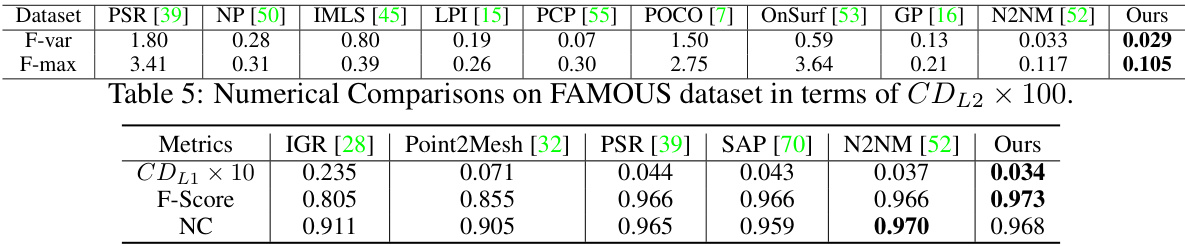
This table presents a numerical comparison of the proposed method’s performance against several state-of-the-art methods on the FAMOUS dataset. The comparison is done using the Chamfer Distance (CDL2) metric, which measures the distance between two point clouds, multiplied by 100. Two variants of the metric are reported: F-var (variance) and F-max (maximum). Lower values indicate better performance in terms of surface reconstruction accuracy.

This table presents the results of experiments conducted to determine the optimal embedding size for the proposed method. Different embedding sizes (128, 256, and 512) were tested, and the Chamfer Distance L2 (CDL2) was used as the evaluation metric. The results show that an embedding size of 256 yields the best performance, suggesting that this size is optimal for capturing the necessary information for accurate signed distance function inference.

This table presents the ablation study on the impact of using a data-driven based prior on the model’s performance. It compares the Chamfer Distance (CDL2) and inference time for four different settings: 1. Without Prior: The model is trained without any prior knowledge. 2. Without Embed: The model uses a random initialization for the embedding vector (c) instead of a learned one. 3. Fixed Param: The model fixes the learned parameters from the pretrained prior (f’) and only optimizes the embedding vector (c). 4. With Prior: The model uses the learned data-driven based prior for initialization and finetunes it during inference.

This table compares the performance of three different local region splitting strategies used in the proposed method for surface reconstruction. The strategies are: uniformly splitting the space into voxel blocks, randomly sampling a fixed-size sphere around a point, and sampling a sphere using KNN to include enough points for reliable statistical reasoning. The metric used for comparison is CDL2 × 100. The results show that the KNN-based sphere approach (Sphere (KNN)) outperforms the other two strategies, achieving the lowest CDL2 error.

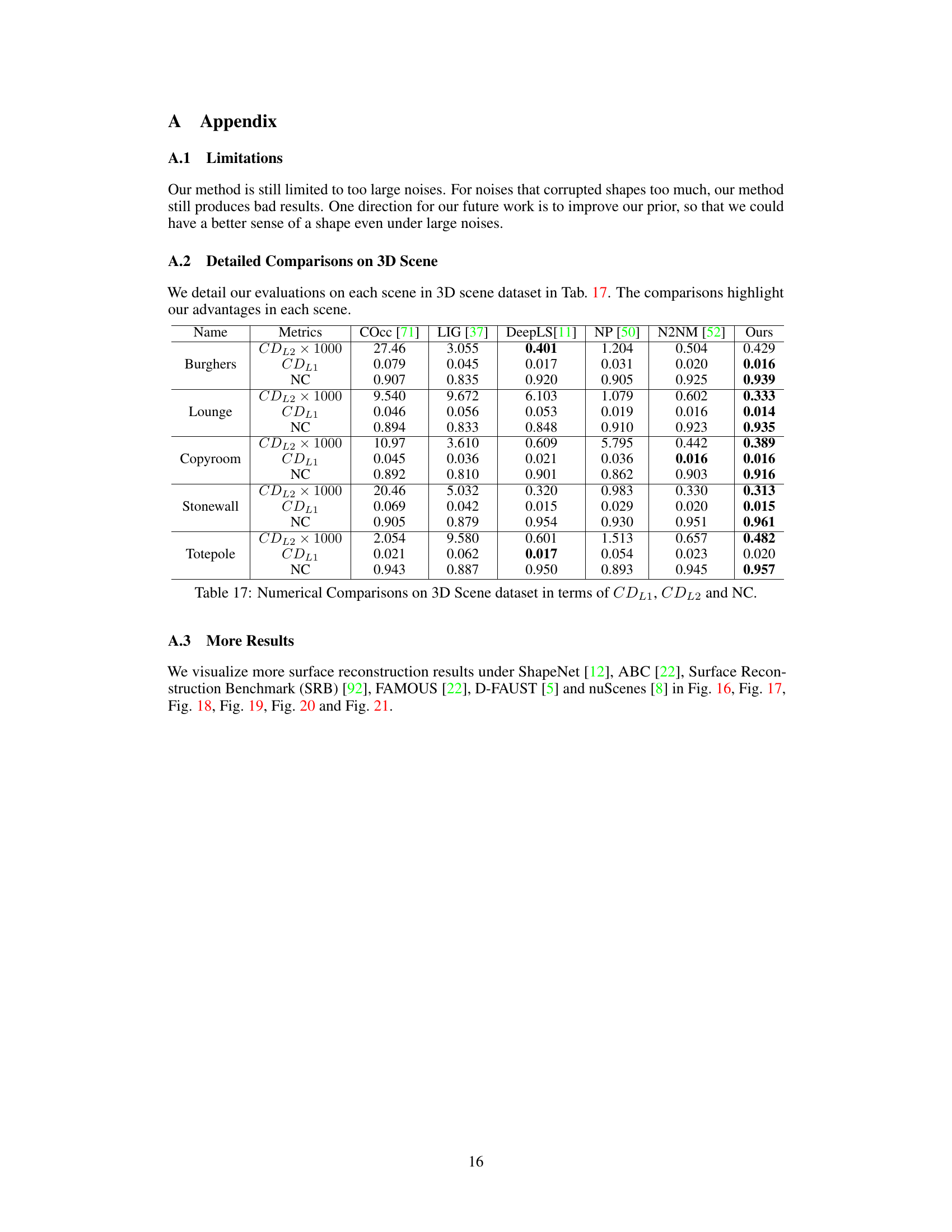
This table presents a numerical comparison of the proposed method against several state-of-the-art techniques for surface reconstruction on the 3D Scene dataset. The metrics used for comparison are Chamfer Distance L1 (CDL1), Chamfer Distance L2 (CDL2), and Normal Consistency (NC). Lower values for CDL1 and CDL2 indicate better surface reconstruction accuracy, while higher values for NC suggest better normal consistency. The table shows that the proposed method outperforms other methods across all metrics, demonstrating its superior performance in surface reconstruction on this specific dataset.
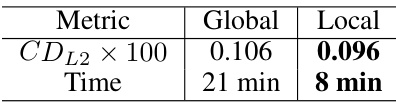
This table compares the performance of the proposed method using global and local mapping strategies during the fine-tuning process. The comparison is made in terms of Chamfer Distance (CDL2) and inference time. It shows that the local mapping strategy significantly improves the result and reduces the inference time.

This table presents the results of an ablation study on the effect of varying the local region size (number of points in a local region) used in the proposed method for inferring neural signed distance functions (SDF). The metric used is the Chamfer Distance (CDL2) multiplied by 100. The results show that a local region size of 1000 yields the best performance, as indicated by the lowest CDL2 value.

This table compares the time consumption of different SDF initialization methods: random, square, sphere (SAL), and the proposed method. The proposed method demonstrates the fastest inference time.

This table presents a comparison of the performance of the proposed method and N2NM [52] under different noise levels. The noise levels are categorized as Middle, Max, and Extreme, representing increasing levels of noise intensity. The metric used for comparison is CDL2 × 100. The results show that the proposed method consistently outperforms N2NM [52] across all noise levels.
This table presents a numerical comparison of different methods for surface reconstruction on the ShapeNet dataset. The metrics used are CDL1 (Chamfer Distance L1) multiplied by 10 for easier reading, NC (Normal Consistency), and F-Score. Lower values of CDL1 indicate better surface reconstruction accuracy, while higher values of NC and F-Score represent better normal consistency and overall surface quality.

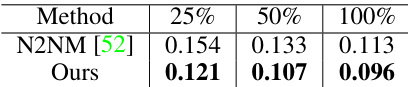
This table shows the inference time of the proposed method with different numbers of points in the input point cloud. The results demonstrate the efficiency of the proposed method, which can handle sparsity and requires less time as the point number decreases.
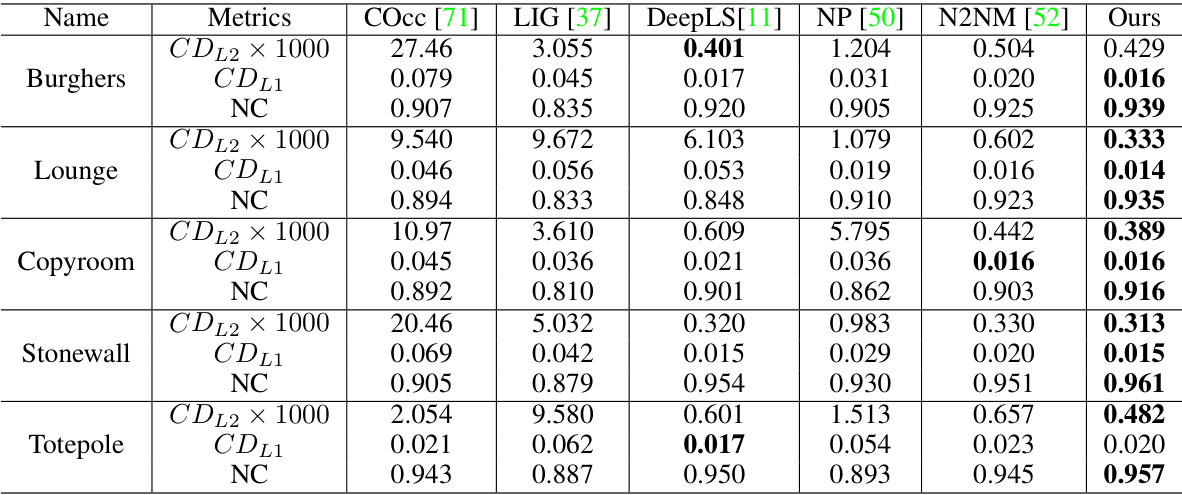
This table presents a quantitative comparison of the proposed method against several state-of-the-art techniques for surface reconstruction on the ShapeNet dataset. The comparison uses three metrics: CDL1 (Chamfer Distance L1) which measures the distance between the reconstructed surface and the ground truth, NC (Normal Consistency) which evaluates the accuracy of normals on the reconstructed surface, and F-Score which combines both metrics. Lower values for CDL1 indicate better surface reconstruction accuracy, and higher values for NC and F-Score represent better normal consistency and overall performance.
Full paper#