Inverse M-Kernels for Linear Universal Approximators of Non-Negative Functions

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it presents the first linear universal approximator for non-negative functions, addressing a major limitation in existing kernel methods. This opens doors for more efficient and flexible models in various applications, particularly where non-negativity constraints are critical such as in density estimation and intensity estimation. It also encourages further research into inverse M-kernels and their properties for multi-dimensional spaces.

Visual Insights

#

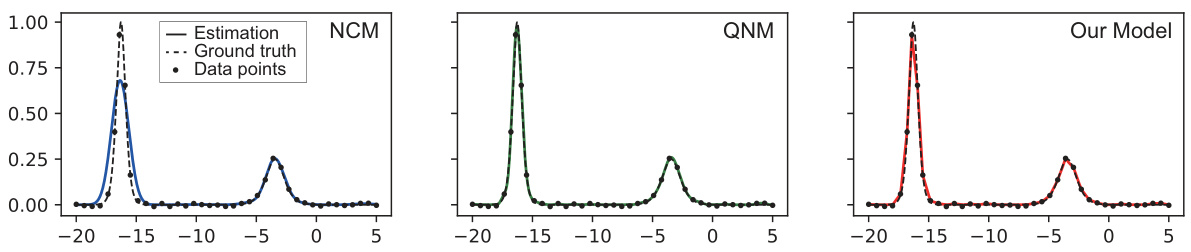
The figure compares the estimated density functions produced by three different methods: NCM, QNM, and the proposed ‘Our Model’, against a ground truth density function. The results are shown for a dataset with noise. Each plot shows the estimated density function overlaid on the ground truth function and data points. The figure demonstrates the ability of the three methods to approximate a bimodal density function and visually displays their performances.

This table presents the results of experiments on KdV data. Three models (NCM, QNM, and the proposed model) were compared across 100 trials with two noise levels (σ = 0.1 and σ = 0.01). The performance is measured using the integrated squared error (l2) between the model’s approximation and the ground truth, and the CPU time (cpu) taken for each trial. Lower l2 values indicate better performance.

In-depth insights

#

Inverse M-kernels

#

The concept of “Inverse M-kernels” introduces a novel class of kernels designed to construct linear universal approximators for non-negative functions. This is a significant departure from traditional kernel methods, which often sacrifice linearity for representational power when handling non-negativity constraints. The key innovation lies in establishing a sufficient condition for positive definite kernels to guarantee the non-negativity of the resulting linear approximator. This condition is linked to the theory of inverse M-matrices, generalizing the concept to kernel functions. The paper demonstrates that certain kernels like exponential/Abel kernels satisfy this condition in one-dimensional spaces, resulting in linear universal approximators. This finding is noteworthy because it addresses the trade-off between linearity (computationally efficient) and flexibility (good representation power), a major challenge in non-negativity-constrained problems. The proposed “Inverse M-kernel models” offer advantages in terms of computational efficiency and maintain good approximation power, potentially surpassing existing methods in specific applications. The extension to higher-dimensional input spaces poses a challenge, requiring further investigation into the conditions that would ensure the creation of inverse M-kernels in such settings.

Linear Approximators

#

The concept of “Linear Approximators” in the context of non-negative function approximation is a central theme. The paper explores the trade-off between achieving linearity (for computational efficiency) and maintaining representational power (accuracy). Existing methods often sacrifice one for the other. For example, non-negative coefficient models (NCM) ensure linearity but lack flexibility, while quadratic methods are flexible but computationally expensive. The core contribution is the introduction of “inverse M-kernels,” a novel class of kernels that allows the construction of linear approximators while addressing non-negativity constraints and maintaining strong representational ability. This offers a unique balance not found in previous approaches. The paper demonstrates how these kernels, particularly exponential kernels, achieve linear universal approximation, a significant improvement. The theoretical foundations are rigorously presented and experimentally validated. However, the current scope is limited to one-dimensional input spaces, leaving extension to higher dimensions as a crucial area for future research. This limitation highlights the complexity of extending this methodology to more practical scenarios.

Non-negativity

#

The concept of non-negativity is central to the paper, focusing on the creation of linear universal approximators that specifically output non-negative functions. This constraint is not trivial; standard kernel methods often produce approximators capable of negative outputs, which is problematic for applications such as density or intensity estimation where only positive values are meaningful. The paper introduces the concept of “inverse M-kernels”, which are positive definite kernels satisfying a sufficient condition to guarantee non-negative outputs from a linear model. This is a key contribution, offering flexible linear models without sacrificing representational power. The authors demonstrate that certain kernels, like exponential kernels, qualify as inverse M-kernels, paving the way for constructing linear universal approximators that are inherently non-negative. This contrasts with previous approaches that either compromised linearity or required computationally expensive non-linear solutions. The practical implications are significant for applications demanding non-negativity, enabling more efficient and robust modeling in fields like signal/image processing, system control, and clinical research.

Universal Approximation

#

The concept of universal approximation, crucial in the study of neural networks and machine learning, is central to the paper’s exploration of non-negative function approximation. The core idea revolves around the ability of a model, given enough capacity (e.g., neurons or kernel functions), to approximate any continuous function within a specified tolerance. This paper investigates whether this powerful capability extends to scenarios where the approximated function must remain non-negative. Linearity versus non-linearity plays a major role; while linear models provide computational advantages, they often sacrifice representational power. The paper explores sufficient conditions on kernel functions, defining them as “inverse M-kernels”, to achieve both linearity and universal approximation of non-negative functions. This is a significant contribution that potentially resolves the existing trade-off between efficient computation and accurate representation in constrained approximation problems.

Future Directions

#

The paper’s core contribution is establishing inverse M-kernels for building linear universal approximators of non-negative functions, primarily focusing on one-dimensional input spaces. A crucial future direction is extending this framework to higher-dimensional inputs. The current approach struggles with the dimensionality challenge, highlighting the need for innovative techniques to maintain linearity and flexibility. Investigating alternative kernel constructions or modifying the inverse M-kernel definition for multi-dimensional spaces is essential. Another important avenue is exploring different loss functions beyond the squared loss to cater to a wider range of non-negative function approximation problems. The impact of various kernel choices and their suitability for specific application domains also requires more exploration. Developing efficient algorithms optimized for higher dimensions is critical for scalability and practical use. Finally, rigorous theoretical analysis of the generalization bounds for multi-dimensional settings is necessary to understand the approximators’ performance in different scenarios.

More visual insights

#

More on figures

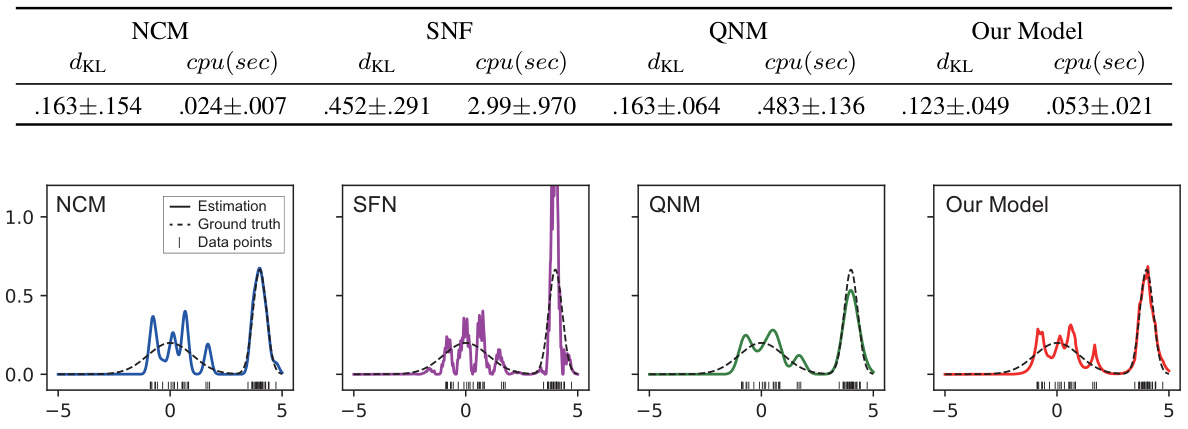
The figure compares the estimated density functions obtained using four different methods: NCM, SNF, QNM, and the proposed ‘Our Model’. Each plot shows the estimated density function (solid line), the ground truth density function (dashed line), and the data points used for estimation (small vertical lines at the bottom). The goal is to visually assess the accuracy and smoothness of each method’s estimation of the density function. Note that SNF significantly overfits, exhibiting multiple local peaks, while Our Model and QNM capture the main features of the bimodal distribution.

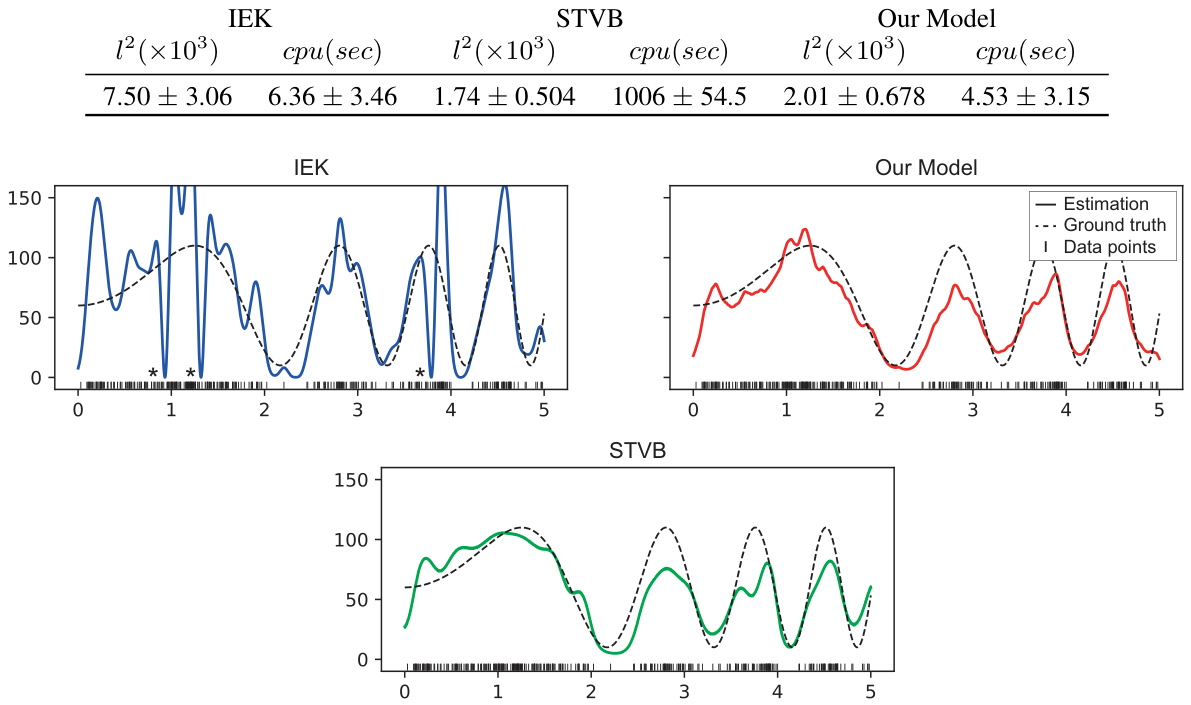
This figure compares the estimated intensity functions obtained using three different methods: IEK (Gaussian kernel intensity estimator), STVB (structured variational Bayesian approach with sigmoidal Gaussian Cox processes), and the proposed IMK (inverse M-kernel model). The x-axis represents the spatial location, and the y-axis represents the intensity. The black dashed line shows the ground truth intensity function, while the colored lines represent the estimations from each method. The asterisks (*) highlight locations where the intensity is zero. The figure visually demonstrates the IMK’s ability to accurately estimate the intensity function, outperforming both IEK and STVB in terms of accuracy and nodal point representation.

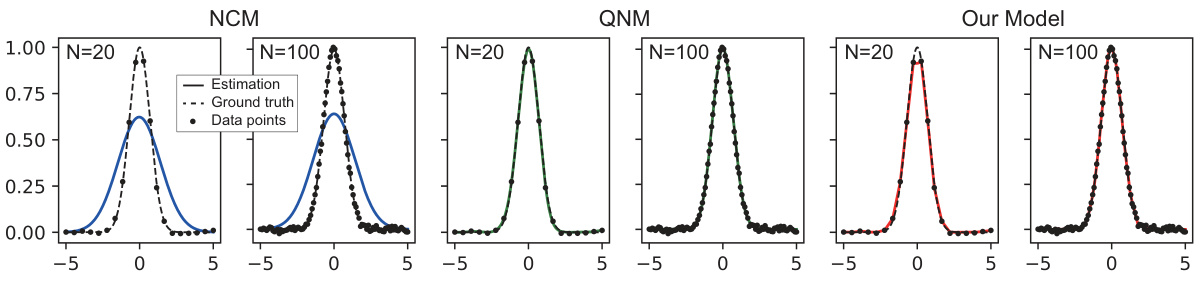
This figure shows the estimated non-negative functions for the ground truth function g(x) = e^-|x|² using three different methods: NCM (Non-negative coefficients Model), QNM (quadratic form of non-negative model), and the proposed Inverse M-kernel model. It compares their performance for two different sample sizes (N=20 and N=100). The plot visually demonstrates the difference in representation power between the methods. It highlights the ability of the proposed Inverse M-kernel model to accurately approximate the ground truth function even with a smaller sample size (N=20), while the other two methods struggle to provide a good fit.

Full paper

#