↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Federated learning (FL) faces challenges with non-IID data, where client data distributions differ significantly. Existing client selection methods for FL struggle to efficiently and effectively handle this heterogeneity. Some approaches incur high computational overheads, while others show reduced efficiency in various heterogeneity scenarios. This significantly impacts model training speed and accuracy.
To overcome these challenges, the authors propose HiCS-FL. This novel client selection method estimates the statistical heterogeneity of a client’s data using output layer updates and uses this information to hierarchically cluster and sample clients. Experiments show that HiCS-FL achieves faster convergence and drastically reduced computation costs compared to other state-of-the-art methods, adapting well to different heterogeneity scenarios.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses the critical challenge of efficient and fast federated learning in non-IID settings. Current methods either suffer from high computational costs or perform poorly under varied data heterogeneity. The proposed HiCS-FL offers a significant improvement by efficiently estimating data heterogeneity and using a hierarchical clustering approach for client selection, paving the way for faster, more efficient federated learning systems.
Visual Insights#
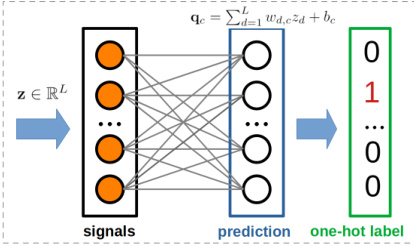
This figure shows the architecture of the last two layers of a neural network used in the HiCS-FL algorithm. The input is a vector z ∈ RL representing the signals from the previous layers. These signals are then multiplied by a weight matrix W ∈ RC×L, and a bias vector b ∈ RC is added. The result is a vector q ∈ RC representing the prediction, where each element corresponds to the logit for a class. Finally, this prediction is compared to a one-hot label representing the true class.

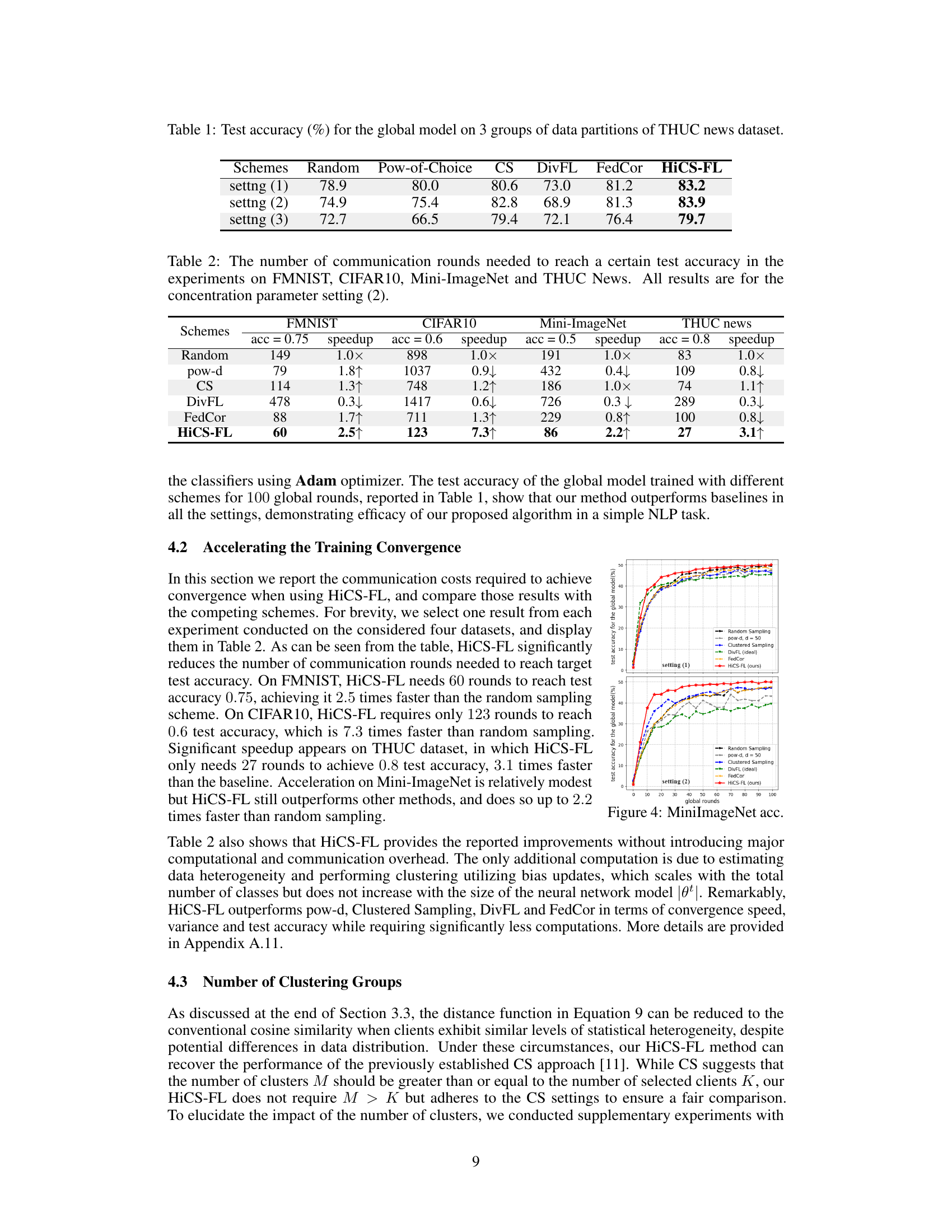
This table shows the number of communication rounds required by different client selection algorithms (random sampling, pow-d, Clustered Sampling, DivFL, FedCor, and HiCS-FL) to achieve a certain test accuracy on four different datasets (FMNIST, CIFAR10, Mini-ImageNet, and THUC News). The results are specifically for the second concentration parameter setting, demonstrating the efficiency of HiCS-FL in terms of communication rounds needed for convergence.
In-depth insights#
Non-IID FL Sampling#
Non-IID federated learning (FL) sampling tackles the challenge of data heterogeneity across client devices. Standard FL algorithms, assuming IID data, struggle in non-IID scenarios where clients possess data drawn from different distributions. This leads to biased model updates and slow convergence. Effective Non-IID FL sampling strategies aim to select clients whose data provides the most informative updates, thus improving model accuracy and training efficiency. Key considerations include balancing diversity (selecting clients with different data distributions) and informativeness (selecting clients with data that significantly contributes to model improvement). Various approaches exist, such as clustering clients based on data similarity and employing strategies that prioritize clients with high model loss or data imbalance. However, a major tradeoff exists between computational efficiency and selection effectiveness. Advanced techniques often introduce significant computational overhead in quantifying data heterogeneity or estimating client informativeness, thereby hindering practical implementation. Future research should focus on developing efficient algorithms that accurately capture data heterogeneity while maintaining low computational cost. This is crucial for scaling FL to large-scale, real-world applications with diverse data distributions.
HiCS-FL Algorithm#
The HiCS-FL algorithm is a novel client sampling method designed to enhance the speed and efficiency of federated learning (FL) in non-IID data settings. It addresses the challenges posed by statistical heterogeneity in FL, where client data distributions differ significantly, and communication resources are limited. Unlike existing methods that either have high computational costs or perform well only under specific heterogeneity scenarios, HiCS-FL leverages a hierarchical clustering approach. The algorithm strategically samples clients based on estimated data heterogeneity, using output layer updates to gauge data balance, which is more computationally efficient. The process involves clustering clients based on a novel distance measure incorporating heterogeneity estimates and then sampling clusters and individual clients with probabilities proportional to their estimated heterogeneity. This adaptive sampling significantly improves convergence speed and reduces variance compared to current state-of-the-art methods across various datasets and heterogeneity levels. Furthermore, HiCS-FL’s inherent adaptability to diverse heterogeneity scenarios makes it a robust and versatile solution for FL.
Heterogeneity Metrics#
In the realm of federated learning, data heterogeneity poses a significant challenge. A crucial aspect of addressing this is the development of robust and informative heterogeneity metrics. These metrics should effectively capture the multifaceted nature of data distribution discrepancies across participating clients. Ideally, a comprehensive metric would incorporate both class imbalance and feature distribution differences. Furthermore, the chosen metric needs to be computationally efficient, readily computable from locally available information (to preserve client privacy), and effectively guide client selection strategies. Methods that rely on output layer gradients or model updates show promise, as they can estimate heterogeneity without explicit access to clients’ sensitive data. However, further research is needed to fully assess the accuracy and robustness of various metrics across diverse datasets and learning tasks. Effective heterogeneity quantification enables smarter client sampling, improving model convergence and generalization performance in non-IID settings.
Convergence Analysis#
A thorough convergence analysis is crucial for evaluating the effectiveness and efficiency of any federated learning algorithm. It involves rigorous mathematical proof to establish the conditions under which the algorithm converges to a solution, and how quickly this convergence occurs. For federated learning, convergence analysis is particularly important due to its unique challenges: non-IID data distributions across clients, communication constraints, and potential device heterogeneity. A robust convergence analysis would ideally examine the impact of these factors on the algorithm’s convergence rate and stability. This should encompass scenarios with varying degrees of data heterogeneity and communication bandwidth, providing insights into the algorithm’s resilience to real-world conditions. Quantifying the convergence rate, in terms of the number of iterations or communication rounds, is essential. Ideally, the analysis would provide bounds on the convergence rate, demonstrating how it scales with the problem’s size and other relevant parameters. Moreover, the analysis should investigate the algorithm’s sensitivity to different initialization strategies, hyper-parameters, and client selection methods. Finally, a strong convergence analysis would also include empirical validation, showing that theoretical bounds align with observed performance in practice across a range of diverse settings.
Future of HiCS-FL#
The future of HiCS-FL (Hierarchical Clustered Sampling for Federated Learning) looks promising, building on its strengths of efficient heterogeneity-guided client sampling. Future research could explore enhancements to the heterogeneity estimation, perhaps incorporating more sophisticated metrics beyond output layer gradients or leveraging techniques from anomaly detection to identify outlier clients with unique data characteristics. Improving the clustering algorithm itself is another avenue, exploring alternative clustering methods or incorporating client dynamics over time. Addressing scenarios with high client churn or significant variations in client participation rates would be crucial for practical applications. Finally, extending HiCS-FL to other FL settings such as those with differential privacy or byzantine clients, or integrating it with other techniques like federated transfer learning, would further expand its applicability and impact.
More visual insights#
More on figures
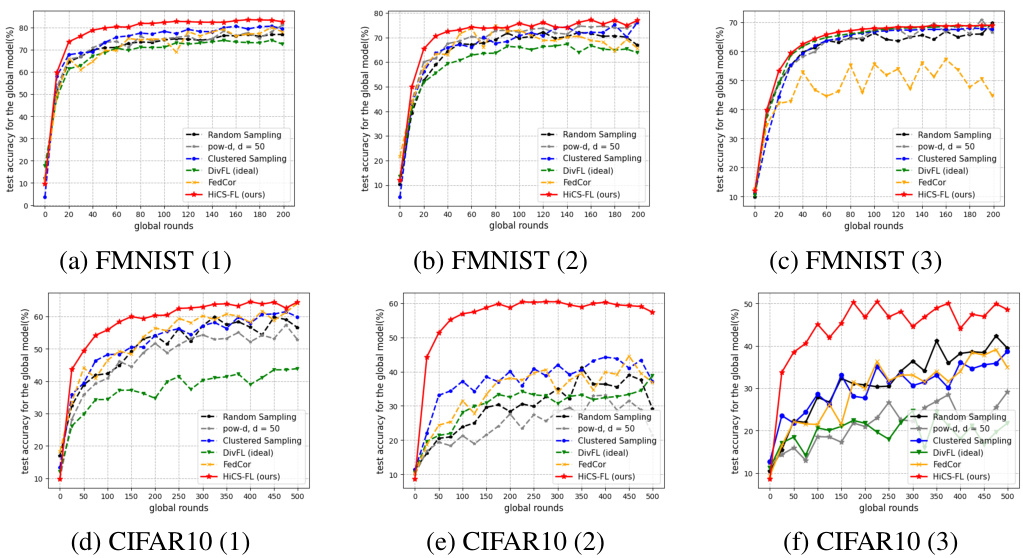
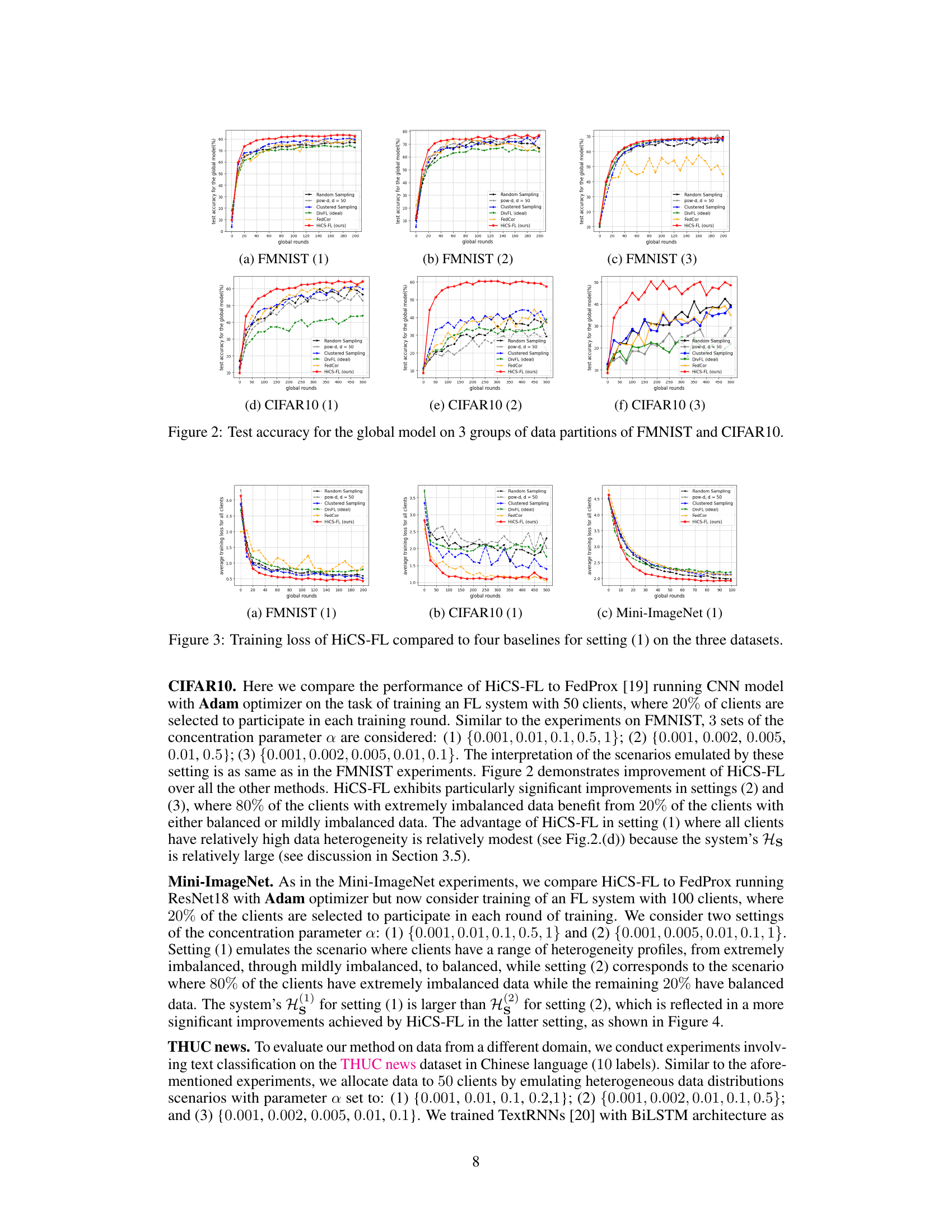
This figure shows the test accuracy of the global model trained using different client selection schemes (random sampling, pow-d, clustered sampling, DivFL, FedCor, and HiCS-FL) across three different data heterogeneity settings for FMNIST and CIFAR10 datasets. Each setting represents a different level of data imbalance across the clients. The results demonstrate the performance of HiCS-FL in comparison to other state-of-the-art methods.
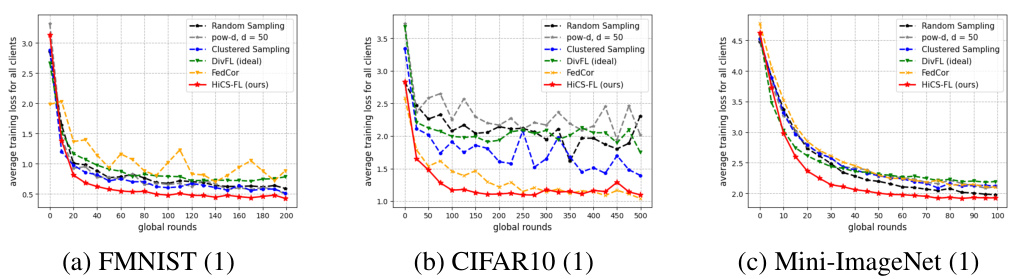
The figure shows the average training loss for all clients across different global training rounds for three benchmark datasets: FMNIST, CIFAR10, and Mini-ImageNet. The performance of HiCS-FL is compared against four baseline methods: random sampling, pow-d, Clustered Sampling, and FedCor. The results are presented for the data partition setting (1), where 80% of the clients have severely imbalanced data while the remaining 20% have balanced data. In all three datasets, HiCS-FL demonstrates significantly faster convergence with lower variance than the other methods.
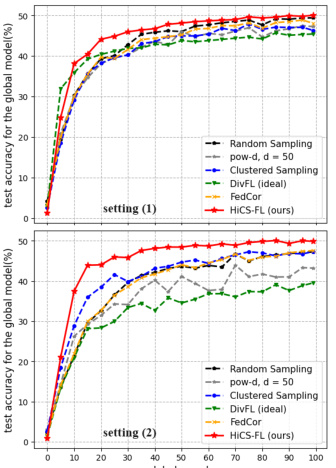
This figure compares the test accuracy of different client selection methods across three different data heterogeneity settings for the FMNIST and CIFAR10 datasets. Setting (1) represents a scenario where 80% of clients have severely imbalanced data while the remaining 20% have balanced data. Setting (2) has 80% of clients with severely imbalanced data and 20% with mildly imbalanced data. Finally, setting (3) has all clients with severely imbalanced data. The plot shows the test accuracy over a certain number of global rounds for each method: Random Sampling, pow-d, Clustered Sampling, DivFL (ideal), FedCor, and HiCS-FL. The results highlight HiCS-FL’s superior performance, particularly in settings with a mix of balanced and imbalanced data, demonstrating its effectiveness in non-IID federated learning scenarios.

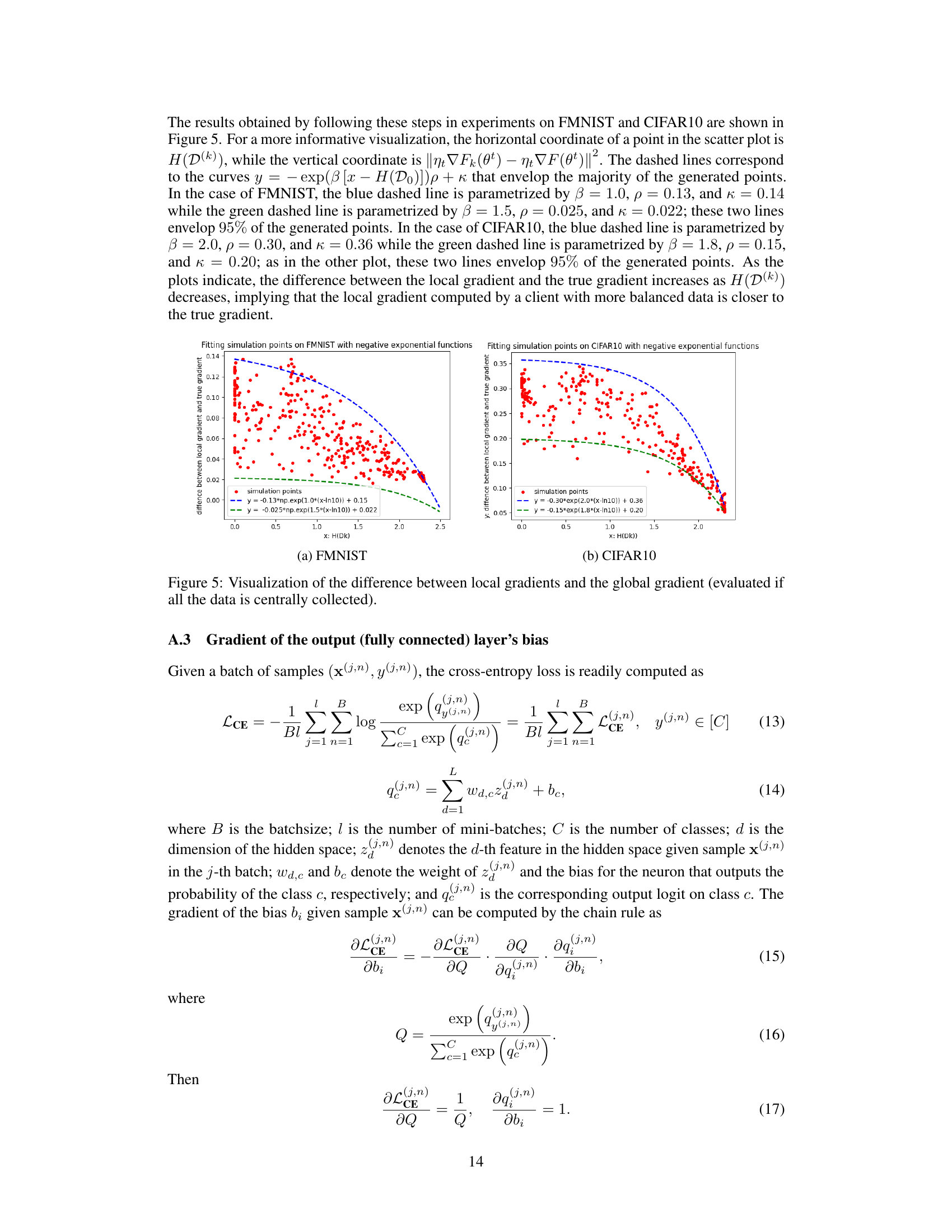
This figure shows the empirical validation of Assumption 3.1, which bounds the dissimilarity between local and global gradients based on data heterogeneity. The plots visualize the relationship between the Shannon entropy of the client’s data label distribution (H(D(k)) on the x-axis) and the squared Euclidean norm of the difference between the local gradient and the true global gradient (on the y-axis) for FMNIST and CIFAR10 datasets. The dashed lines represent negative exponential functions fitted to the data points, demonstrating that the difference between local and global gradients increases as the data label distribution becomes more imbalanced (i.e., H(D(k)) decreases). This visually confirms Assumption 3.1, supporting the theoretical analysis of HiCS-FL.
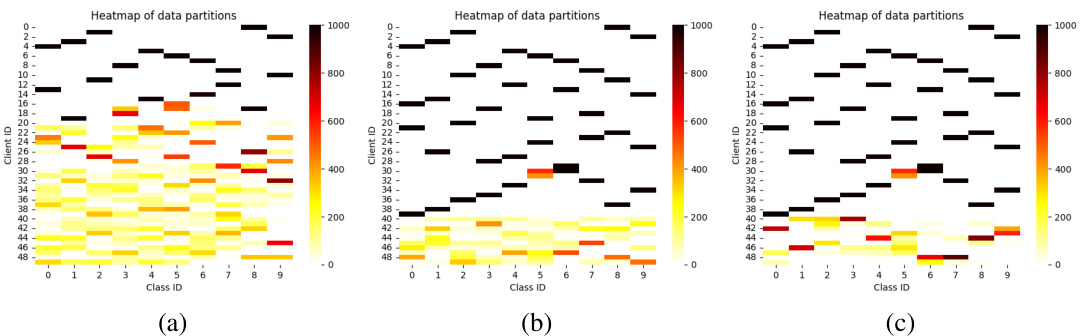
This figure shows the data distribution across 50 clients in CIFAR10 for three different levels of heterogeneity. Each subfigure represents a different setting of the concentration parameter α in the Dirichlet distribution used to generate non-IID data. Each cell in the heatmap represents the number of samples of a certain class owned by a specific client. The color intensity indicates the number of samples; darker colors represent more samples.
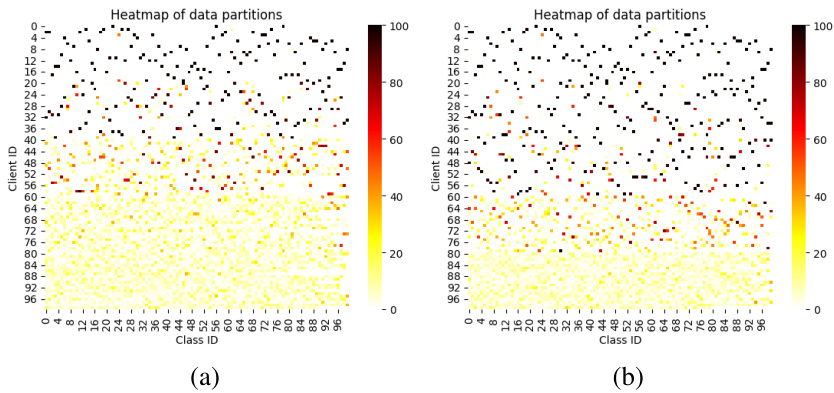
This figure shows the class distribution of training data across 50 clients in CIFAR10 dataset under three different settings of data heterogeneity controlled by Dirichlet distribution concentration parameter α. Each subfigure shows a heatmap where rows represent clients, columns represent classes, and color intensity represents the number of samples in each class per client. The three settings represent different levels of data heterogeneity; from most heterogeneous (a) to least heterogeneous (c).
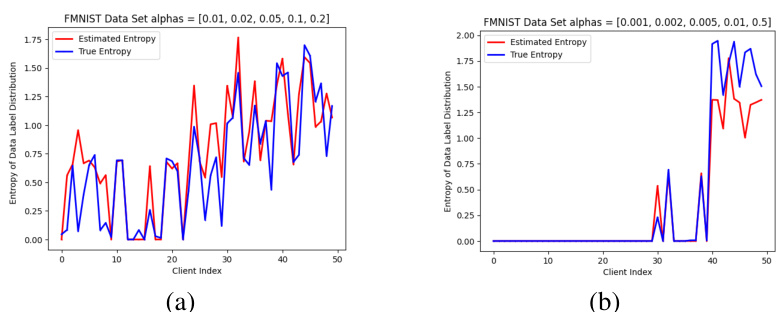
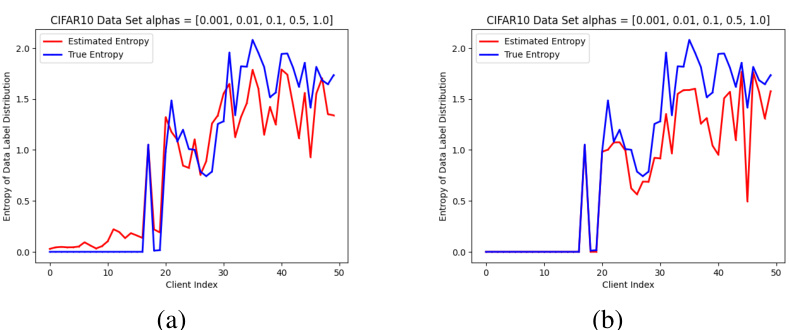
This figure shows the estimated entropy of data label distribution in experiments on the FMNIST dataset using SGD optimizer. It compares the estimated entropy (red line) against the true entropy (blue line) for two different settings of the concentration parameter α. The concentration parameter α controls the level of data heterogeneity; smaller α leads to more imbalanced data distributions. The plot visually demonstrates the relationship between the estimated entropy and the true entropy for various data distributions, providing empirical support for the accuracy of the proposed heterogeneity estimation method within the HiCS-FL framework.
This figure compares the test accuracy of different federated learning client selection methods across three different data heterogeneity scenarios for the FMNIST and CIFAR10 datasets. The x-axis represents the number of global training rounds, and the y-axis represents the test accuracy of the global model. Each line represents a different client selection method (Random Sampling, pow-d, Clustered Sampling, DivFL, FedCor, and HiCS-FL). The three subfigures (a), (b), and (c) correspond to different data heterogeneity levels in FMNIST, while (d), (e), and (f) correspond to those in CIFAR10. HiCS-FL consistently outperforms other methods, achieving faster convergence and lower variance, particularly in scenarios with a mixture of balanced and highly imbalanced data among clients.
The figure shows the test accuracy for the global model trained with different schemes for three different data partition settings of FMNIST and CIFAR10 datasets. Each setting represents a different level of data heterogeneity among the clients, ranging from severely imbalanced data to balanced data. The results demonstrate the performance of HiCS-FL in comparison with other state-of-the-art client selection methods. HiCS-FL outperforms other methods across different settings, exhibiting the fastest convergence rates and the least amount of variance, particularly significant when there is a mix of balanced and imbalanced data among clients.
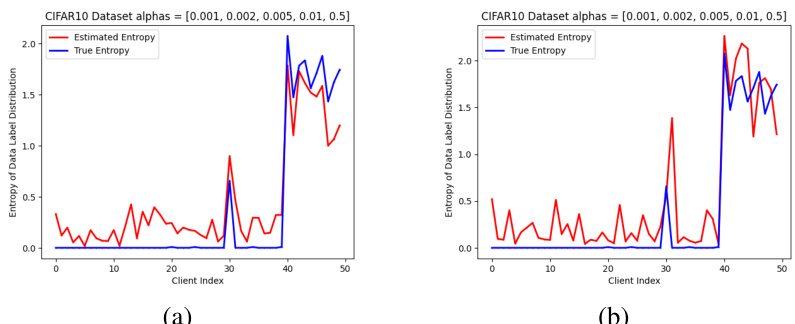
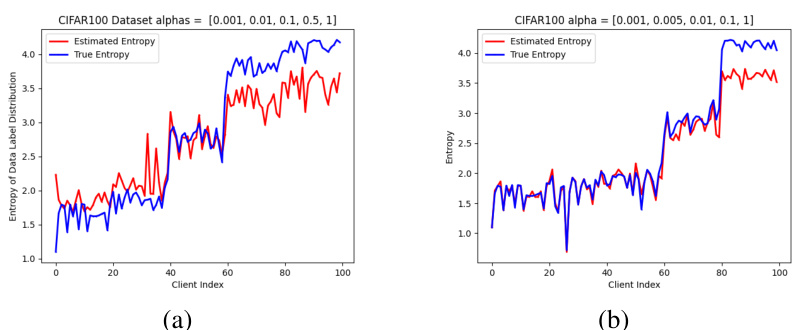
This figure compares the estimated entropy of data label distribution with the true entropy for two different optimizers (SGD and Adam) on the CIFAR10 dataset. The data is partitioned using a Dirichlet distribution with concentration parameter α = [0.001, 0.002, 0.005, 0.01, 0.5]. The x-axis represents the client index, and the y-axis represents the entropy. The red line shows the estimated entropy, and the blue line shows the true entropy.
More on tables

This table presents the test accuracy results achieved by different client selection schemes on the THUC news dataset. Three different data heterogeneity settings are considered, with varying degrees of class imbalance among clients. The results show how each client selection method performs under different levels of data heterogeneity. The ‘setting’ column specifies the level of heterogeneity, with (1) representing more balanced data, and (3) representing more imbalanced data. HiCS-FL consistently outperforms the other methods, demonstrating its effectiveness in handling diverse data heterogeneity scenarios.
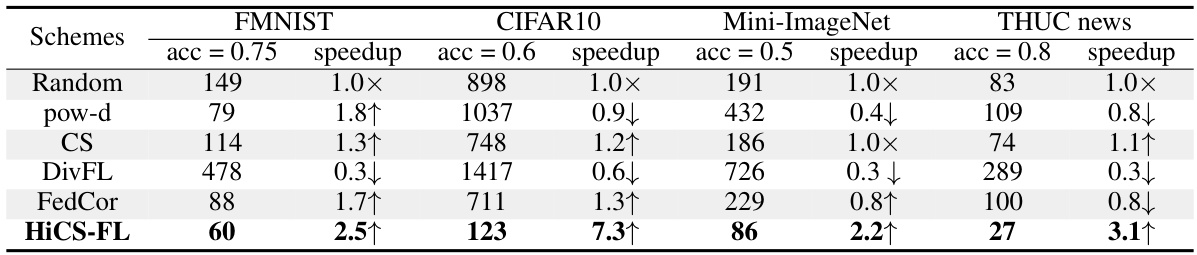
This table shows the number of communication rounds required to achieve a certain test accuracy for four different datasets (FMNIST, CIFAR10, Mini-ImageNet, and THUC News) using different client selection methods. The speedup is calculated relative to the random sampling method. A lower number of rounds indicates faster convergence.

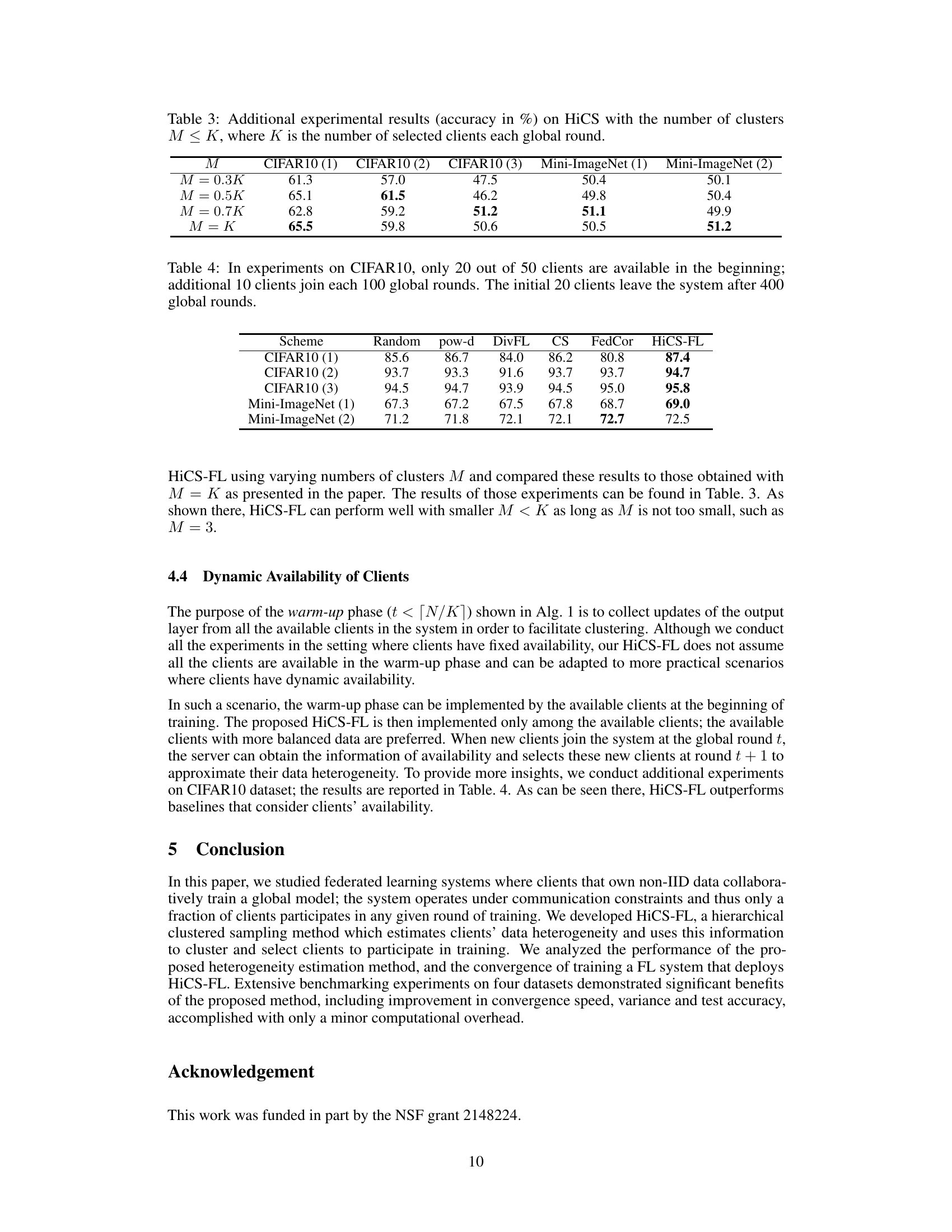
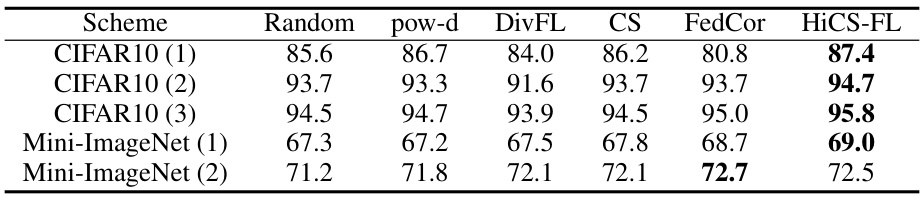
This table presents the accuracy results of the HiCS-FL algorithm under different numbers of clusters (M) compared to the number of selected clients per round (K). It shows how the accuracy changes as the ratio of M to K varies. The results are presented for different datasets and heterogeneity scenarios, indicated by CIFAR10 (1), CIFAR10 (2), CIFAR10 (3), Mini-ImageNet (1), and Mini-ImageNet (2). These different scenarios likely represent various levels of data heterogeneity across clients.
This table presents the test accuracy results (%) on CIFAR10 and Mini-ImageNet datasets under a dynamic client availability setting. In this setting, initially, only 20 out of 50 clients are available for training. Then, every 100 global rounds, 10 more clients join the training process, while the initial 20 clients leave after 400 global rounds. The table compares the performance of HiCS-FL against several baseline methods, showcasing its robustness in scenarios with fluctuating client participation.

This table compares the computational and communication complexities of different client sampling methods in federated learning. It shows the additional computational and communication overhead of each method compared to a baseline of random sampling. The complexity is expressed using Big O notation, where |θt| represents the size of the global model parameters at round t, and C represents the number of classes. HiCS-FL shows significantly lower computational overhead than other methods.
Full paper#