↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Adapting reinforcement learning (RL) policies from simulated to real-world environments is challenging due to discrepancies in dynamics. Existing domain adaptation methods require extensive interactions with real environments and are thus impractical in safety-critical applications. Offline domain calibration provides a more promising approach but suffers from low sample efficiency due to reliance on evolutionary algorithms.
This paper introduces Madoc, a multi-agent domain calibration framework. Madoc formulates domain calibration as a cooperative multi-agent RL problem, leveraging a variational autoencoder to cluster similar parameters and a bandit RL objective to match target trajectory distributions. Experiments on locomotion tasks demonstrate Madoc’s superior performance, highlighting its efficiency and effectiveness over other offline and hybrid online-offline approaches.
Key Takeaways#
Why does it matter?#
This paper is important because it tackles the critical challenge of domain adaptation in reinforcement learning, a significant hurdle in real-world applications. By introducing a novel multi-agent framework, it offers a highly efficient and sample-efficient solution to calibrate RL policies for deployment in new environments with limited target domain data. This work has the potential to advance various fields like robotics, healthcare, and autonomous driving, where extensive data collection can be expensive or unsafe.
Visual Insights#

This figure illustrates the Madoc framework. It begins with an imperfect source domain and offline data from the target domain. The source domain data is used to train a VAE which clusters similar physics parameters into groups, represented by different agents. These agents cooperatively learn calibration policies using MARL to adjust the source domain parameters, aiming to match the target trajectory distribution. The calibrated source domain is then used to train a final policy via an online RL algorithm, which can then be directly deployed in the target domain.
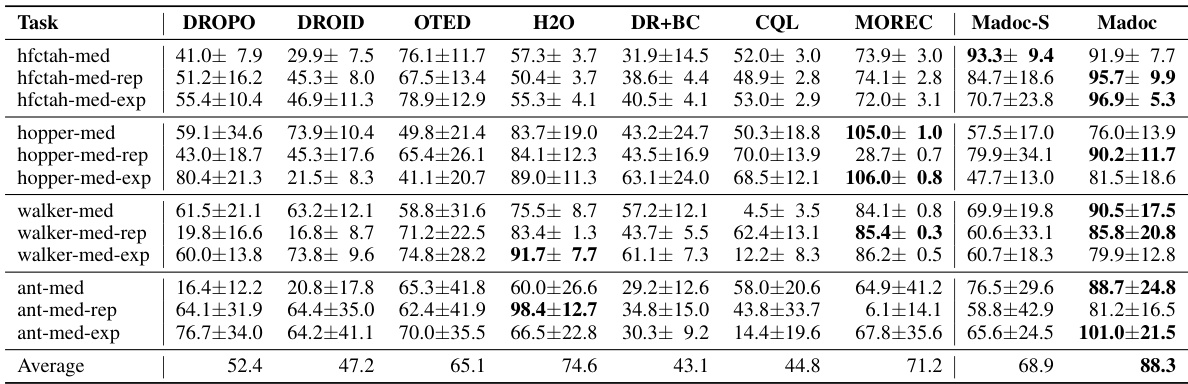
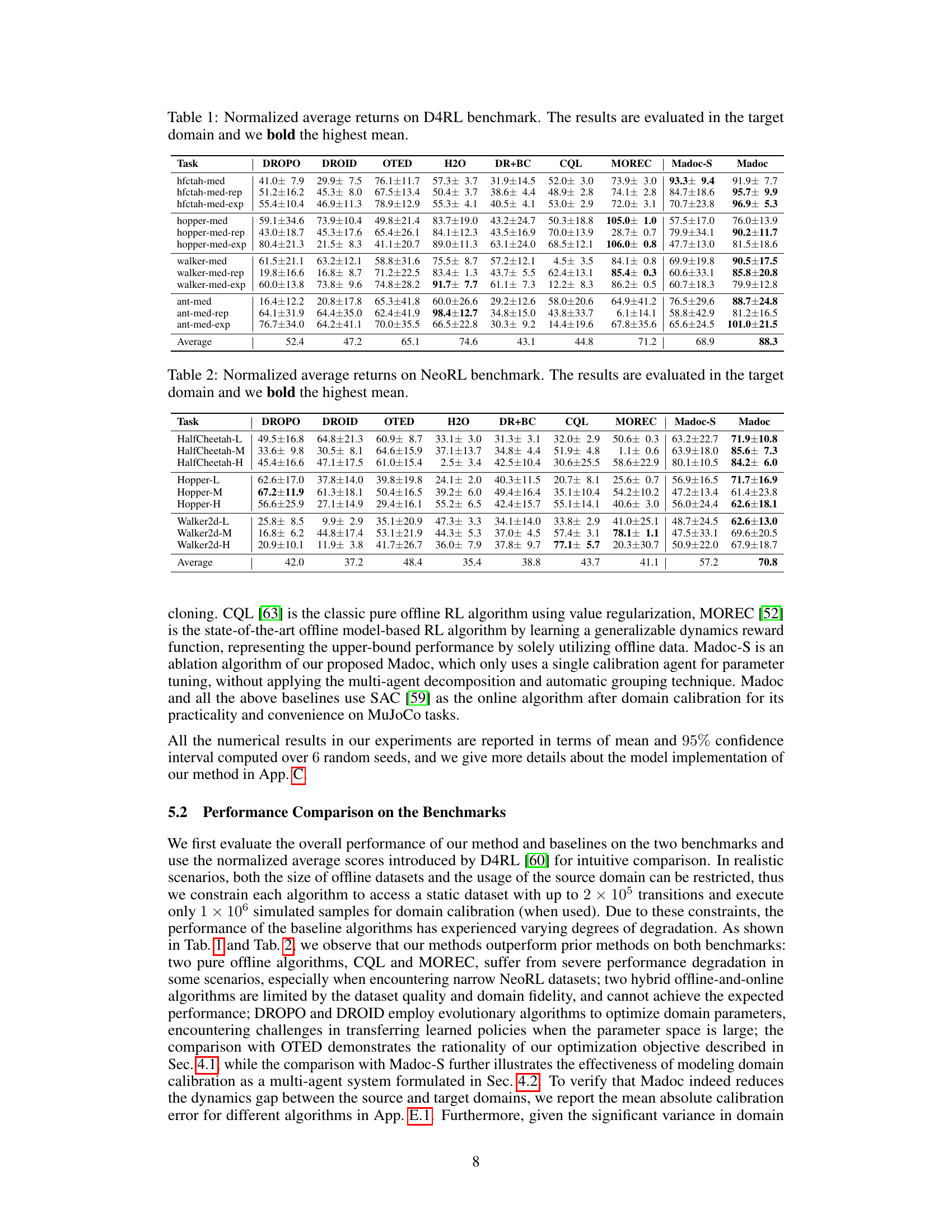
This table presents the normalized average returns achieved by different reinforcement learning algorithms on the D4RL benchmark. The results are obtained in the target domain, indicating the performance of each algorithm when transferring a policy trained in a source domain to the target domain. The highest average return for each task is bolded, enabling a quick comparison of algorithm performance across multiple tasks and dataset variations.
In-depth insights#
Offline Domain Cal.#
Offline domain calibration addresses the challenge of adapting reinforcement learning (RL) agents trained in a source domain (e.g., simulation) to perform well in a different target domain (e.g., real-world) using only offline data from the target domain. This is crucial because online adaptation in the target domain may be infeasible or unsafe in many real-world applications. The core idea is to calibrate the source domain’s parameters, such as physical properties in a simulator, to better match the target domain’s dynamics. This enables the direct deployment of the pre-trained policy without further online fine-tuning. Methods for offline domain calibration often focus on efficiently searching the large space of possible parameter adjustments, and this is where challenges lie. Existing approaches often rely on computationally expensive methods like evolutionary algorithms. Improved techniques would strive for higher sample efficiency and scalability to handle complex domains with many parameters, perhaps leveraging techniques like multi-agent reinforcement learning (MARL) or advanced optimization algorithms to address the challenges of this high-dimensional parameter space.
Multi-Agent MARL#
Employing a multi-agent approach within the framework of multi-agent reinforcement learning (MARL) presents a powerful strategy for tackling the inherent complexities of domain calibration. This technique allows for the decomposition of the large domain parameter space into smaller, more manageable sub-problems, each handled by an individual agent. This not only enhances efficiency by reducing search space but also allows for a more nuanced understanding of the interplay between different parameters, as each agent learns to calibrate its parameters while cooperating with others. The cooperative nature of the MARL framework allows agents to leverage collective knowledge and improve performance beyond what a single-agent approach could achieve. This multi-agent structure is particularly valuable when dealing with numerous interconnected physics parameters in complex real-world scenarios where the influence of a single parameter often isn’t independent. The VAE-based clustering method further streamlines the process by automatically grouping parameters with similar effects, thereby optimizing agent assignments and enhancing calibration performance. The overall framework demonstrates a significant improvement in sample efficiency and robustness compared to single-agent methods, making it highly suitable for deployment in real-world applications.
VAE Parameter Grouping#
The ‘VAE Parameter Grouping’ section likely details a crucial preprocessing step. A Variational Autoencoder (VAE) is used to automatically cluster physics parameters based on their effect on the simulated environment’s dynamics. This is essential because directly optimizing all parameters simultaneously in a high-dimensional space is computationally expensive and inefficient. The VAE learns a lower-dimensional representation where similar parameters cluster together, effectively reducing the search space. This clustering simplifies the subsequent multi-agent reinforcement learning (MARL) process, allowing each agent to focus on a smaller, more manageable subset of parameters. The choice of VAE highlights the need for a method that can capture complex relationships between parameters, potentially uncovering hidden structure in the parameter space that might otherwise be overlooked. The success of this grouping is vital for the efficiency and effectiveness of Madoc, since ineffective grouping would likely lead to suboptimal performance or failure to converge in the MARL phase.
Bandit RL Objective#
In the context of multi-agent domain calibration, a bandit RL objective offers a powerful approach to aligning a source domain’s dynamics with those of a target domain using limited offline data. The core idea is to formulate domain calibration as a trajectory distribution matching problem. Instead of directly optimizing complex physics parameters, a bandit RL framework allows the indirect optimization by learning a set of classifiers. These classifiers serve as a reward model, evaluating how well simulated trajectories from the source domain match real-world trajectories from the target domain. This reward signal guides the learning process, effectively transforming the complex high-dimensional parameter calibration into a simpler reward maximization problem within a bandit framework. The advantage is that it circumvents the need for precise system dynamics modeling. The proposed bandit RL objective is particularly well-suited to handle situations with numerous physics parameters, reducing the complexity of the calibration process and enhancing its sample efficiency. The use of classifiers adds robustness and avoids direct dependence on often-unavailable accurate or precise target domain dynamics models.
Future Work: Vision#
The heading ‘Future Work: Vision’ suggests a focus on the long-term goals and aspirations for the research. It implies a shift from immediate objectives towards a more ambitious, potentially transformative vision. This could involve exploring the applicability of the current methods to complex real-world scenarios like autonomous driving or robotics, which require more robust and generalizable approaches. Furthermore, it might encompass the development of new algorithms and architectures specifically tailored for visual data processing in domains with high dimensionality and noise. Exploring novel ways to leverage unlabeled or weakly labeled data for training and calibration is another promising avenue. Improving the sample efficiency of the methods would be critical, possibly through incorporating techniques like transfer learning or meta-learning. Finally, the ‘vision’ might involve integrating the current work with other areas like causal inference or explainable AI to produce more trustworthy and understandable systems.
More visual insights#
More on figures
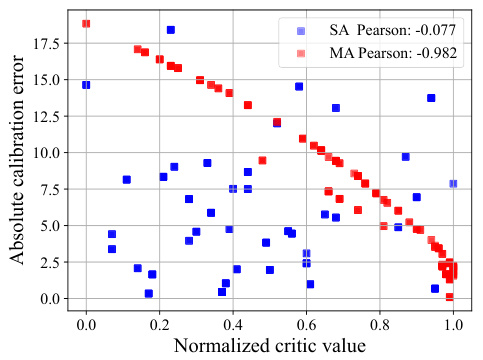
This figure shows the Pearson correlation between the critic value for the gravity coefficient and the absolute calibration error. Each point represents a sampled action, where the critic value is computed by feeding the action into the corresponding critic. The plot demonstrates that a stronger negative correlation exists between critic value and absolute calibration error for the multi-agent (MA) method, indicating that the multi-agent approach is better at identifying and reducing errors than the single-agent (SA) approach.
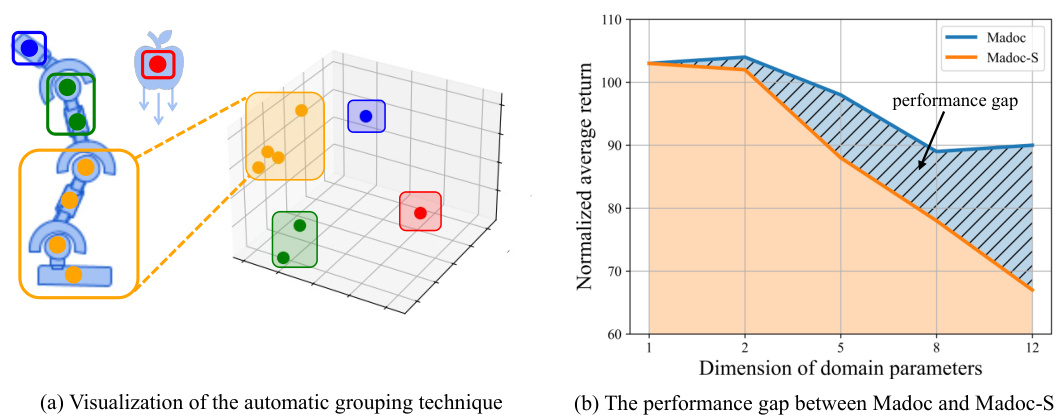
This figure visualizes the automatic grouping of physics parameters in the Madoc algorithm and compares the performance of Madoc and its single-agent counterpart (Madoc-S). (a) shows how similar parameters are grouped together based on their effect on the robot’s dynamics. (b) demonstrates the performance gap between Madoc and Madoc-S increases with the number of parameters to be calibrated, highlighting the efficiency of Madoc’s multi-agent approach.
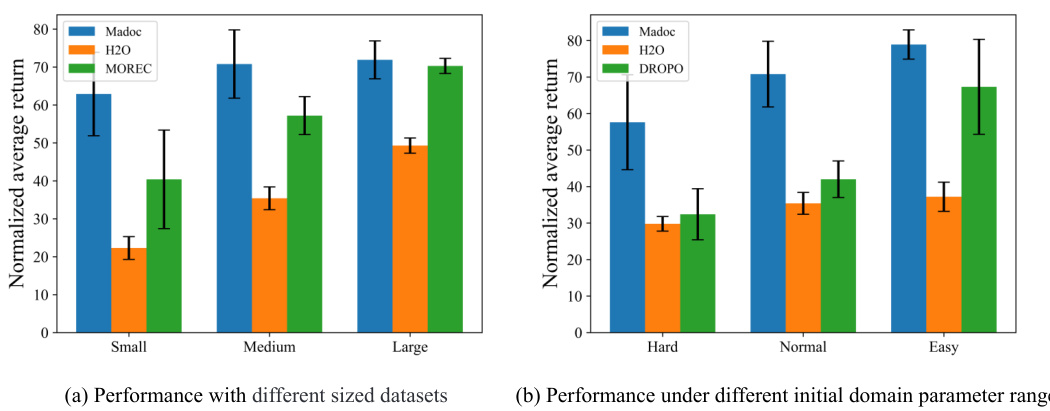
This figure shows the performance of Madoc and several baseline algorithms across datasets of varying sizes and with different initial parameter ranges of the source domain. Subfigure (a) compares the performance on the NeoRL benchmark using small, medium, and large datasets; demonstrating Madoc’s robustness to data size. Subfigure (b) shows performance variations when different initial ranges (hard, normal, easy) for the domain parameters are used, highlighting Madoc’s ability to handle varying degrees of parameter uncertainty.

This figure illustrates the Madoc framework’s workflow. It shows how simulated data from a source domain and offline data from a target domain are used to calibrate the source domain’s parameters. The process involves using a variational autoencoder (VAE) for parameter grouping and multi-agent reinforcement learning (MARL) for calibration.

Figure 3(a) visualizes the automatic grouping of physics parameters in the Hopper robot, showing how parameters with similar effects are clustered. Figure 3(b) compares the performance of Madoc and its single-agent variant (Madoc-S) on the Ant environment, demonstrating Madoc’s improved efficiency with increasing parameter dimensions.

This figure visualizes the automatic grouping technique used in Madoc and compares its performance with a single-agent approach (Madoc-S). Panel (a) shows how physics parameters of the Hopper robot are clustered into groups based on their similar effects on the dynamics. Panel (b) demonstrates that the multi-agent approach (Madoc) outperforms the single-agent approach (Madoc-S), especially as the number of parameters increases, highlighting the efficiency and fidelity gains achieved by the multi-agent strategy.

This figure illustrates the Madoc framework for multi-agent domain calibration. It shows the flow of simulated data from the source domain and offline data from the target domain. The source domain is calibrated using a multi-agent reinforcement learning approach (MARL) to match the target trajectory distribution. Different colors represent simulated data, offline data, and the calibration process. The agents cooperate to adjust multiple parameters simultaneously.
More on tables
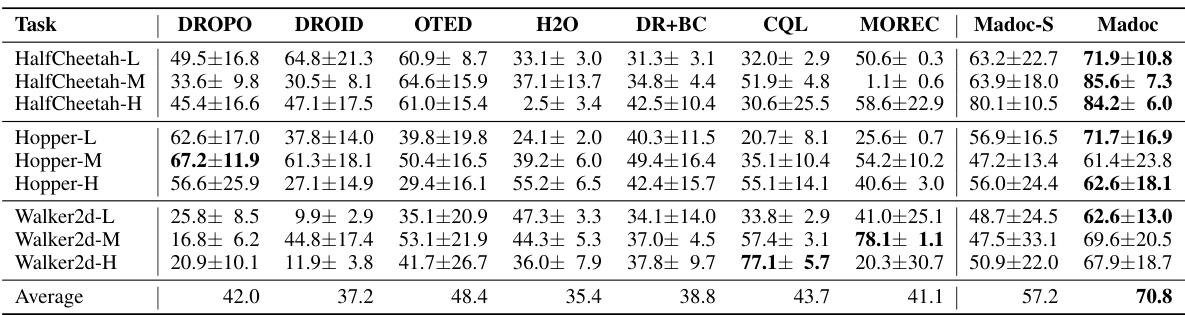
This table presents the results of the proposed Madoc algorithm and several baseline algorithms on the NeoRL benchmark. The ‘Normalized average returns’ represent a performance metric, adjusted to allow comparison across different tasks. The results are evaluated in the target domain (the real-world environment the algorithm is ultimately intended for). The highest average return for each task is bolded to easily highlight the best performing algorithm for each task.

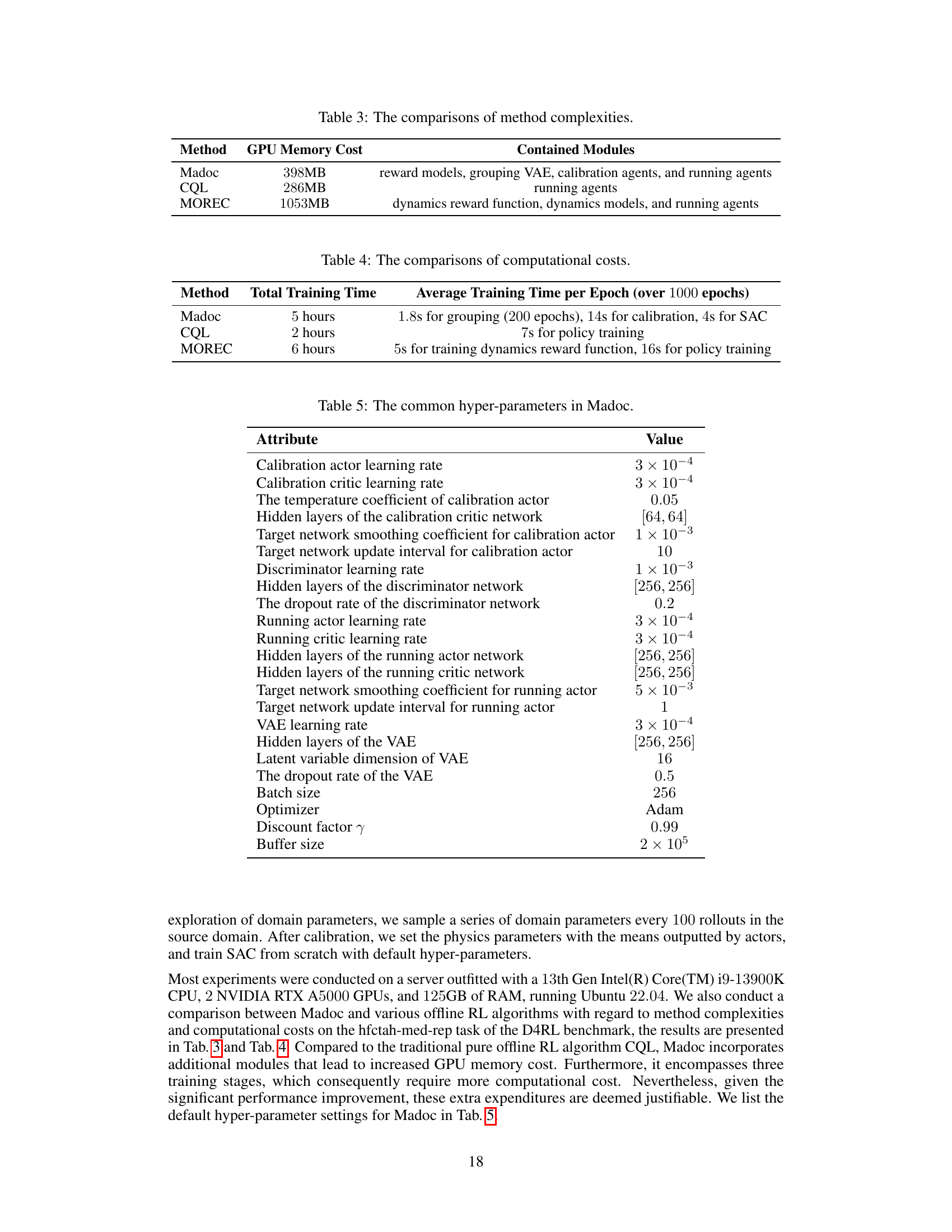
This table compares the GPU memory cost and modules of three different methods: Madoc, CQL, and MOREC. Madoc has the highest memory cost because it includes reward models, a Variational Autoencoder (VAE) for parameter grouping, multiple calibration agents, and running agents. CQL uses only running agents, resulting in the lowest memory cost. MOREC falls between the two, incorporating a dynamics reward function, dynamics models, and running agents.

This table presents the normalized average returns achieved by different reinforcement learning algorithms on the D4RL benchmark. The results are specifically for the target domain, showing how well policies trained in a source domain generalize. The highest mean return for each task is bolded to highlight the top-performing algorithms. The D4RL benchmark includes variations in dataset quality, providing a comprehensive evaluation.

This table presents the results of the normalized average returns achieved by different algorithms on the D4RL benchmark. The experiments were conducted on the target domain, and the highest mean for each task is highlighted in bold. The table allows for a direct comparison of the performance of Madoc against various baseline methods across multiple locomotion tasks and dataset variations.
This table presents the normalized average returns achieved by different reinforcement learning algorithms on the D4RL benchmark. The results are broken down by task (HalfCheetah, Hopper, Walker, Ant) and dataset type (medium, medium-replay, medium-expert). Higher values indicate better performance. The table highlights the superior performance of Madoc compared to other methods.
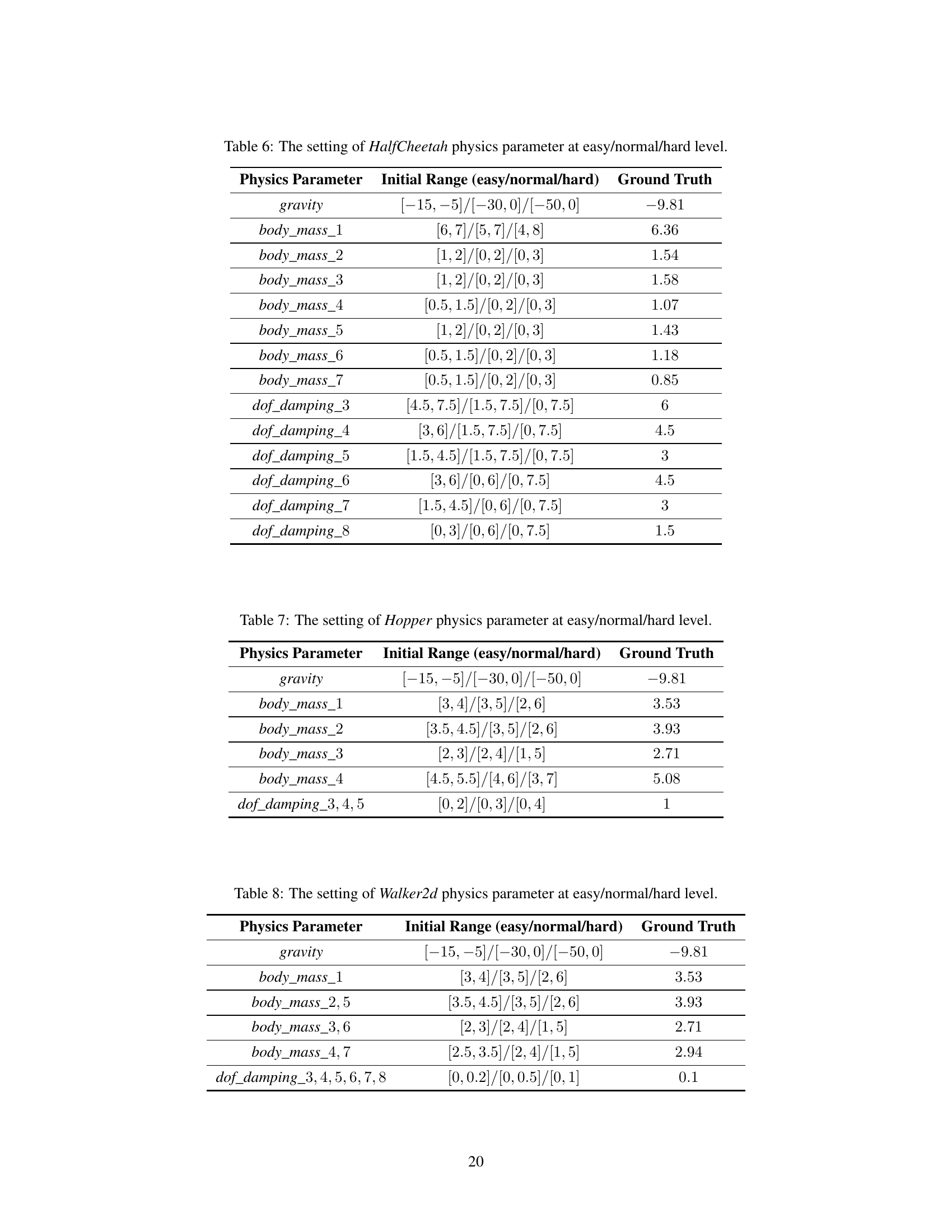
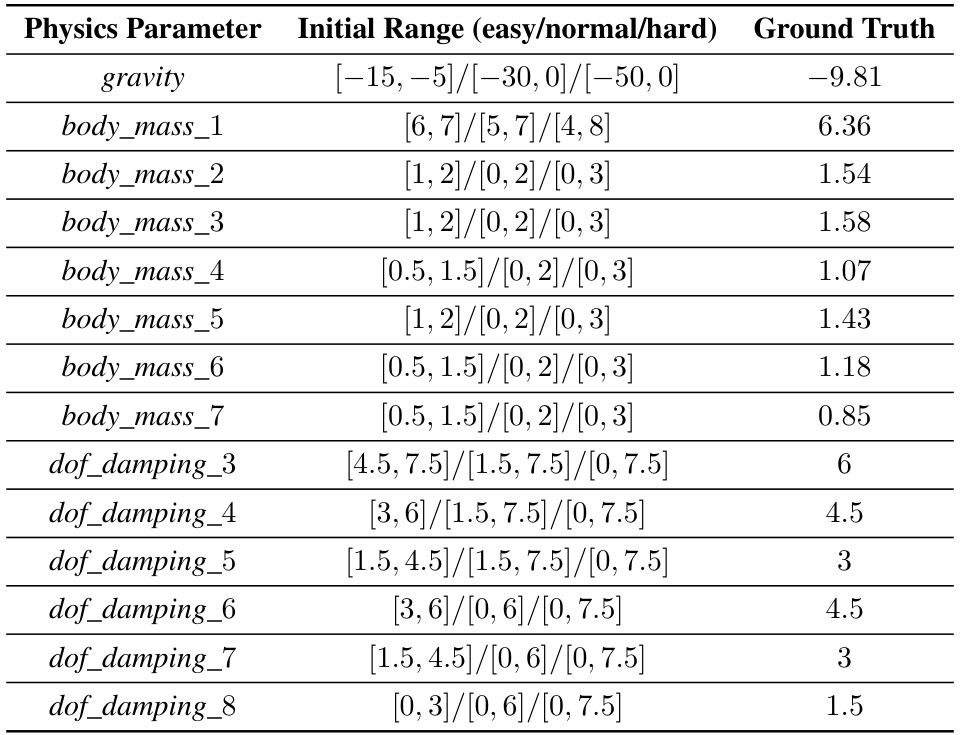
This table shows the initial range and ground truth values for various physics parameters of the Hopper robot in a simulation environment. The parameters are categorized into three levels of difficulty: easy, normal, and hard. The initial ranges represent the bounds within which the physics parameter values can vary during the simulation, while the ground truth values are the actual values used in the real-world environment. This table is crucial for understanding how the difficulty levels influence the calibration process in the Madoc framework.

This table presents the normalized average returns achieved by different reinforcement learning algorithms on the D4RL benchmark. The results are specifically for the target domain, and the highest average return for each task is highlighted in bold. The table compares Madoc’s performance against several other state-of-the-art methods across various locomotion tasks and dataset variations (medium, medium-replay, and medium-expert).

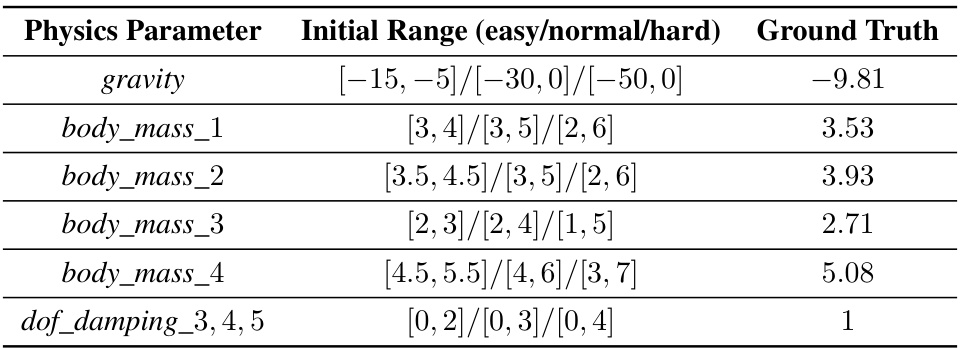
This table shows the initial range and ground truth values for various physics parameters of the Ant robot in the simulation environment. The parameters include gravity, and the mass of different body parts. These values are used to calibrate the source domain model to match the target domain.

This table shows the mean absolute calibration error for different algorithms on the D4RL benchmark. The error is a measure of how far the calibrated source domain parameters are from the true target domain parameters. Lower values indicate better calibration and thus better transfer performance to the target domain. The results are broken down by task and dataset (medium, medium-replay, medium-expert) within each task. The lowest mean error for each task and dataset is bolded.

This table presents the normalized average returns achieved by different algorithms on the D4RL benchmark. The results are specifically measured in the target domain to evaluate the performance of each method after domain transfer. The highest mean for each task is highlighted in bold.

This table presents the normalized average returns achieved by various algorithms on the D4RL benchmark. The results represent the performance of each algorithm in the target domain (real-world environment). The ‘highest mean’ return for each task is bolded, highlighting the best-performing algorithm for that particular task.
Full paper#