TL;DR#
Offline Reinforcement Learning (RL) faces challenges when training agents using datasets from multiple, potentially suboptimal experts. Existing methods often struggle to effectively learn from such data, leading to inefficient policies. The distribution shift between the learned policy and the behavior policies in the dataset causes instability and hinders performance. This paper addresses these issues by proposing a novel algorithm. This new approach re-imagines offline RL as an optimal transport problem. By using the Q-function as a cost and the policy as a transport map, the researchers create a maximin optimization problem.
The proposed algorithm, called Partial Policy Learning (PPL), directly trains a policy to identify the best expert actions for each state. This avoids cloning suboptimal behaviors, improving policy extraction. PPL is evaluated on continuous control problems using the D4RL benchmark. The results show significant improvements over existing methods, demonstrating the effectiveness of the proposed approach.
Key Takeaways#
Why does it matter?#
This paper is important because it offers a novel perspective on offline reinforcement learning by framing it as an optimal transport problem. This approach addresses the limitations of existing methods that struggle with suboptimal expert data, opening up new avenues for research in offline RL and potentially improving the performance of RL agents in real-world applications where online learning is costly or risky. It also presents a new algorithm, Partial Policy Learning (PPL), which demonstrates improved performance compared to state-of-the-art model-free offline RL techniques.
Visual Insights#
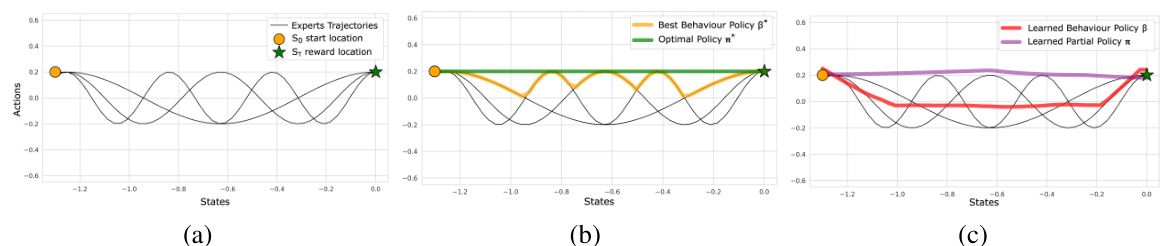
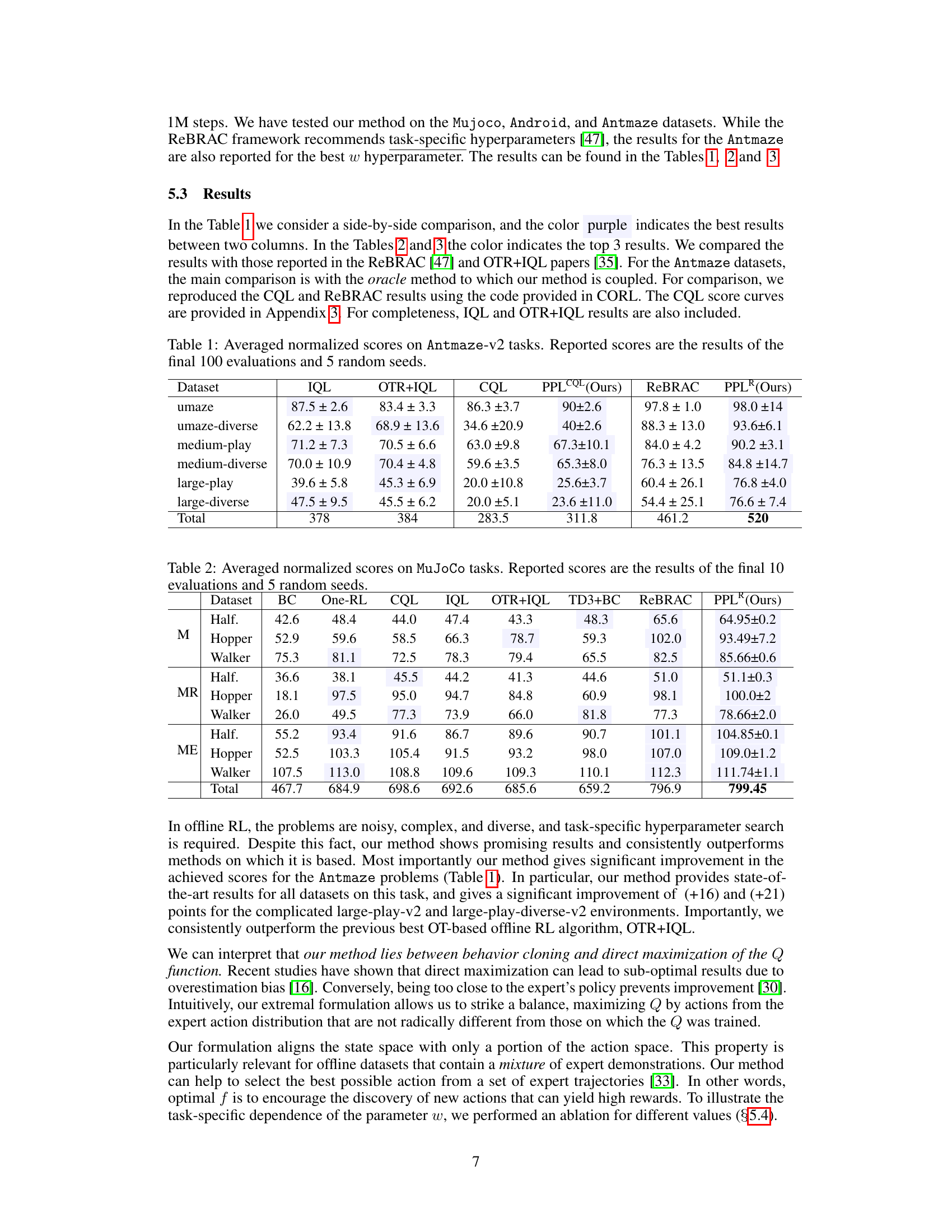
🔼 This figure demonstrates the results of the proposed Partial Policy Learning (PPL) algorithm on a simplified toy environment. Panel (a) shows several suboptimal expert trajectories attempting to reach a reward location. Panel (b) contrasts these with the best observed behavior and the true optimal policy. Panel (c) finally shows how the proposed PPL algorithm and standard behavior cloning approach perform in comparison to the true optimal.
read the caption
Figure 1: Toy experiments. (a) Left point S0 denoting start and ST is the only rewarded, target location. Black curves visualize behavior trajectories β. (b) Best behavior policy β* according to the data, and the optimal policy π* that provides the optimal (shortest path) solution. (c) Results of the policy β trained by minimizing −Qβ(s,π(s)) + BC and policy π trained by our algorithm 1.
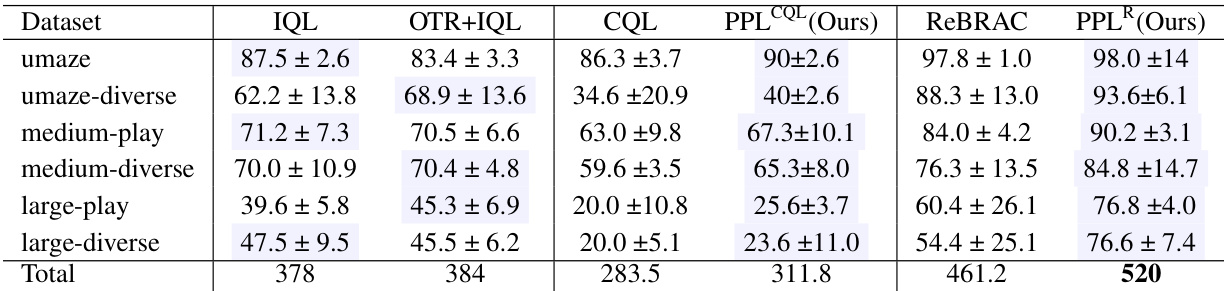
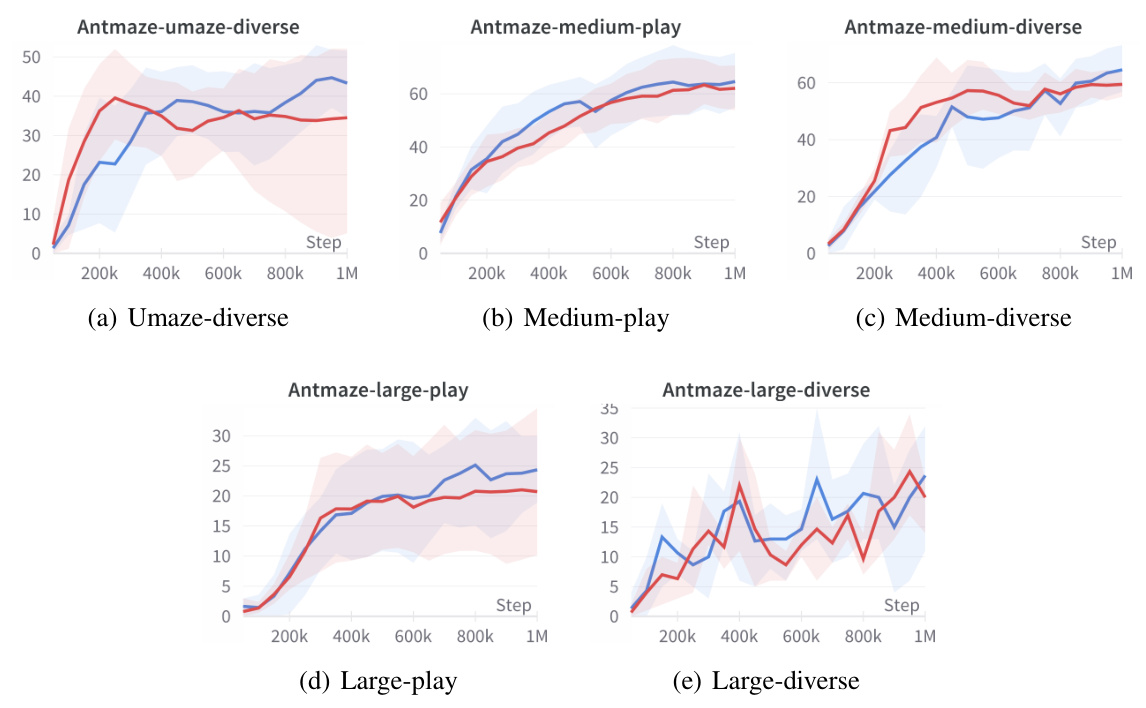
🔼 This table presents the averaged normalized scores achieved by different offline reinforcement learning algorithms on Antmaze-v2 tasks. The scores are averages across 100 final evaluations, with 5 random seeds used for each algorithm. The algorithms compared include IQL, OTR+IQL, CQL, the proposed PPL algorithm (both with CQL and ReBRAC cost functions), ReBRAC, and the proposed PPLR algorithm. The table provides a quantitative comparison of the performance of the proposed methods against state-of-the-art baselines on this specific set of benchmark tasks.
read the caption
Table 1: Averaged normalized scores on Antmaze-v2 tasks. Reported scores are the results of the final 100 evaluations and 5 random seeds.
In-depth insights#
OT in Offline RL#
Optimal Transport (OT) offers a novel perspective for offline reinforcement learning (RL) by framing the problem as finding an optimal mapping between state and action distributions. Instead of directly cloning behavior policies, which can be suboptimal when dealing with diverse or imperfect expert demonstrations, OT elegantly focuses on stitching together the best actions from various expert trajectories. This approach is particularly powerful in scenarios where datasets include suboptimal expert behaviors. By leveraging the Q-function as a cost function and the policy as the transport map, offline RL becomes a Maximin OT optimization problem, which can efficiently identify optimal actions for each state. Partial OT further refines this approach, allowing the algorithm to focus only on the most relevant parts of the action distribution. This results in a method robust to the presence of noisy or inefficient data in the dataset, providing a compelling alternative to standard behavior cloning techniques.
Partial Policy Learn#
Partial Policy Learning (PPL) represents a novel approach to offline reinforcement learning that cleverly addresses the challenge of suboptimal expert demonstrations within datasets. Instead of directly imitating all expert behaviors, which may include inefficient actions, PPL leverages optimal transport to selectively learn a policy that maps states to a partial distribution of the best expert actions. This is achieved by framing offline reinforcement learning as a maximin optimal transport problem, where the Q-function acts as the transport cost and the learned policy becomes the transport map. The algorithm cleverly integrates partial optimal transport, ensuring the policy only learns from the most relevant and efficient actions, thereby enhancing its overall performance. This approach, by avoiding the detrimental impact of suboptimal expert data, effectively stitches together the most rewarding expert behaviors, leading to superior policy extraction and improved performance in offline reinforcement learning settings.
RL as OT Problem#
Reframing reinforcement learning (RL) as an optimal transport (OT) problem offers a novel perspective on offline RL. The core idea is to view the policy as an optimal transport map, and the Q-function as the transport cost. This allows leveraging OT’s strengths in efficiently mapping probability distributions, especially when dealing with diverse or suboptimal expert data. Instead of directly cloning expert behavior, which can be inefficient with noisy data, this approach focuses on identifying and stitching together the best actions from various experts for each state. This is achieved by formulating the problem as a maximin OT optimization, which effectively extracts a partial distribution of the most optimal expert actions for each state. This contrasts with previous OT-based RL approaches that primarily use OT as a regularization technique or reward function. By rethinking the entire offline RL problem through the lens of OT, this framework offers a powerful and flexible method to overcome the limitations of traditional offline RL algorithms.
Stitching with POT#
The concept of ‘Stitching with Partial Optimal Transport (POT)’ presents a novel approach to offline reinforcement learning. It addresses the challenge of datasets containing suboptimal expert demonstrations by selectively integrating the best actions from various experts, rather than simply cloning the entire behavior. This stitching process uses POT, which allows for partial mapping of states to actions. Unlike prior OT methods that focus on full distribution matching or regularization, this approach leverages POT’s ability to strategically select only the most beneficial actions based on a cost function (often a learned critic), effectively mitigating negative influence from suboptimal expert data. This leads to a policy that learns a better representation of optimal behavior. The method elegantly combines the strengths of optimal transport with reinforcement learning to build robust and effective offline policies.
D4RL Experiments#
The section ‘D4RL Experiments’ would likely detail the empirical evaluation of a novel offline reinforcement learning algorithm on the Deep Data-Driven Reinforcement Learning (D4RL) benchmark. This would involve a rigorous comparison against multiple state-of-the-art offline RL methods. Key aspects would include the specific D4RL environments used (e.g., continuous control tasks like Walker, Hopper, HalfCheetah, or discrete tasks), a clear description of the baselines used for comparison, and a presentation of the quantitative results, such as average returns or success rates. A crucial part would be the analysis of the results, discussing the algorithm’s performance relative to the baselines, providing explanations for any significant differences, and identifying scenarios where the proposed method excels or falls short. Furthermore, the experimental setup would be described in detail (hyperparameters, training procedures), ensuring reproducibility. The discussion may also cover potential limitations of the experiments, and address issues such as the dataset size or diversity, and any biases present. Finally, ablation studies or sensitivity analyses varying key parameters, potentially including the effect of dataset size and quality, would help uncover insights into the algorithm’s robustness and behavior in varying settings.
More visual insights#
More on figures
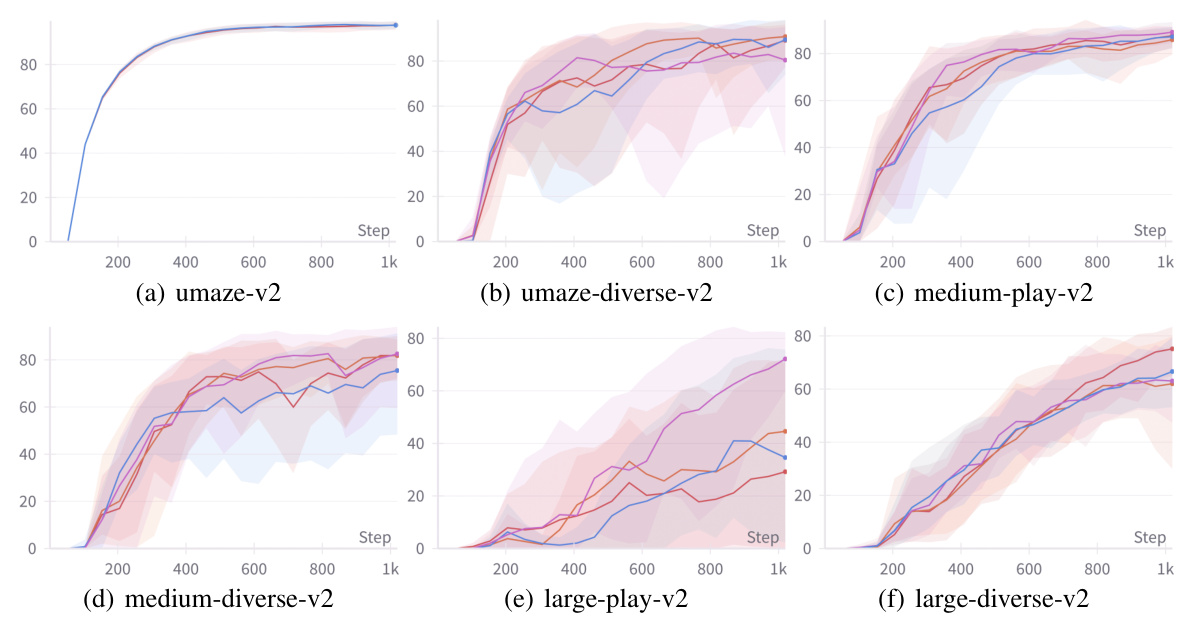
🔼 This figure shows a comparison of different policies in a simple toy environment. The goal is to find the shortest path from a starting point (S0) to a reward location (ST). Panel (a) displays the trajectories followed by three suboptimal expert policies. Panel (b) shows the optimal policy (π*) that achieves the shortest path and the best policy (β*) found in the data among the experts. Panel (c) contrasts the performance of a behavior cloning policy (β) and the policy (π) learned by the proposed algorithm. The proposed algorithm outperforms the behavior cloning policy by finding a path closer to the optimal solution.
read the caption
Figure 1: Toy experiments. (a) Left point S0 denoting start and ST is the only rewarded, target location. Black curves visualize behavior trajectories β. (b) Best behavior policy β* according to the data, and the optimal policy π* that provides the optimal (shortest path) solution. (c) Results of the policy β trained by minimizing −Qβ(s, π(s)) + BC and policy π trained by our algorithm 1.
🔼 This figure shows a comparison of different policies on a simple toy environment. Part (a) displays the environment and example trajectories of suboptimal behavior policies. Part (b) illustrates the optimal policy (π*) and the best policy found in the data (β*). Part (c) compares the performance of a behavior cloning policy (β) with the proposed Partial Policy Learning (PPL) algorithm (π), highlighting the PPL algorithm’s ability to extract a better policy by stitching together elements from the dataset.
read the caption
Figure 1: Toy experiments. (a) Left point S0 denoting start and ST is the only rewarded, target location. Black curves visualize behavior trajectories β. (b) Best behavior policy β* according to the data, and the optimal policy π* that provides the optimal (shortest path) solution. (c) Results of the policy β trained by minimizing -Qβ(s, π(s))+BC and policy π trained by our algorithm 1.
More on tables
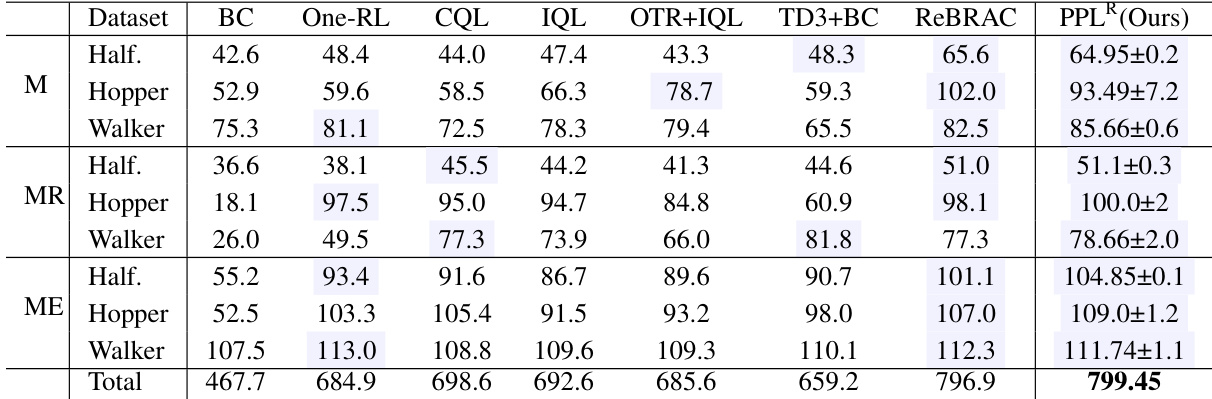
🔼 This table presents the average normalized scores achieved by different offline reinforcement learning algorithms on three MuJoCo continuous control tasks: HalfCheetah, Hopper, and Walker. The scores are averages over 10 final evaluations and 5 random seeds, offering a robust comparison of algorithm performance. Algorithms compared include behavior cloning (BC), One-Step RL, Conservative Q-Learning (CQL), Implicit Q-Learning (IQL), IQL with Optimal Transport Reward Labeling (OTR+IQL), Twin Delayed Deep Deterministic Policy Gradient with behavior cloning (TD3+BC), ReBRAC, and the proposed Partial Policy Learning (PPL) method. The table allows for a quantitative assessment of the relative effectiveness of each algorithm on these benchmark tasks.
read the caption
Table 2: Averaged normalized scores on MuJoCo tasks. Reported scores are the results of the final 10 evaluations and 5 random seeds.
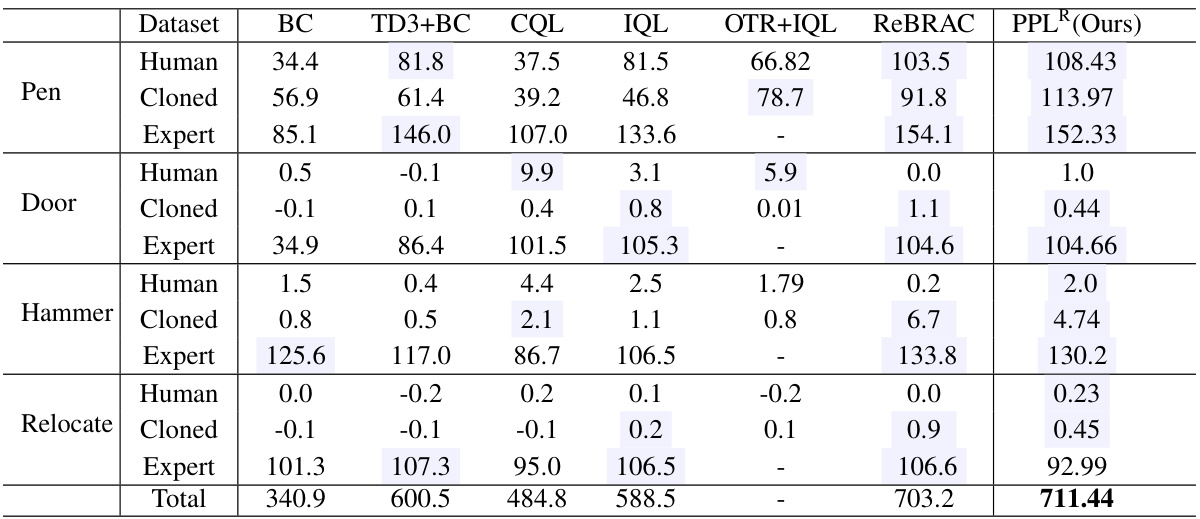
🔼 This table presents the averaged normalized scores achieved by different offline reinforcement learning algorithms on Android tasks from the D4RL benchmark. The scores represent the average performance across 5 random seeds and the final 100 evaluation steps. The algorithms compared include Behavior Cloning (BC), Twin Delayed Deep Deterministic Policy Gradient with behavior Cloning (TD3+BC), Conservative Q-Learning (CQL), Implicit Q-Learning (IQL), IQL with Optimal Transport Reward Labeling (OTR+IQL), ReBRAC, and the proposed Partial Policy Learning (PPLR). The table is broken down by task (Human, Cloned, Expert) for each environment (Pen, Door, Hammer, Relocate).
read the caption
Table 3: Averaged normalized scores on Android tasks. Reported scores are the results of the final 10 evaluations and 5 random seeds.

🔼 This table presents the averaged normalized scores achieved by the OneStep-RL and PPL (Partial Policy Learning) algorithms on three different MuJoCo tasks: HalfCheetah, Hopper, and Walker. The results are further broken down into three dataset categories: Medium, Medium-Replay, and Medium-Expert, representing variations in the data used for training. Each score is an average over 10 final evaluations and 5 random seeds, offering a measure of statistical reliability. The table highlights the performance differences between OneStep-RL and the proposed PPL method across various scenarios.
read the caption
Table 4: Averaged normalized scores on MuJoCo tasks. Results of the final 10 evaluations and 5 random seeds.

🔼 This table shows the optimal values of the hyperparameter ‘w’ for different environments in the D4RL benchmark suite. The hyperparameter ‘w’ controls the size of the action subspace considered by the Partial Policy Learning (PPL) algorithm. Different environments may require different values of ‘w’ to achieve optimal performance, reflecting the varying complexities and characteristics of the datasets.
read the caption
Table 5: Optimal w values for different environments
Full paper#