↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Graph Neural Networks (GNNs) are powerful tools, but their training often relies on backpropagation, which has biological implausibility and efficiency issues. This creates challenges for scalability and parallel processing, particularly when dealing with non-Euclidean graph data. Existing non-backpropagation methods have limitations when directly applied to GNNs.
The paper introduces DFA-GNN, a novel forward learning framework that addresses these challenges. DFA-GNN uses a dedicated forward training mechanism and extends the principles of Direct Feedback Alignment (DFA) to GNNs. It incorporates graph topology into feedback links to handle non-Euclidean data and uses a pseudo-error generator for semi-supervised learning, effectively spreading errors from labeled nodes to unlabeled ones. Extensive experiments demonstrate its superior performance and robustness against various types of noise and attacks, outperforming both traditional BP and other non-BP approaches.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses limitations of backpropagation in training graph neural networks (GNNs), offering a novel forward learning framework (DFA-GNN) that is more biologically plausible, efficient, and robust to noise and attacks. It opens new avenues for GNN research and development, especially in semi-supervised learning scenarios. Its excellent performance on various benchmarks and its adaptability to different GNN architectures showcase its significant potential impact.
Visual Insights#
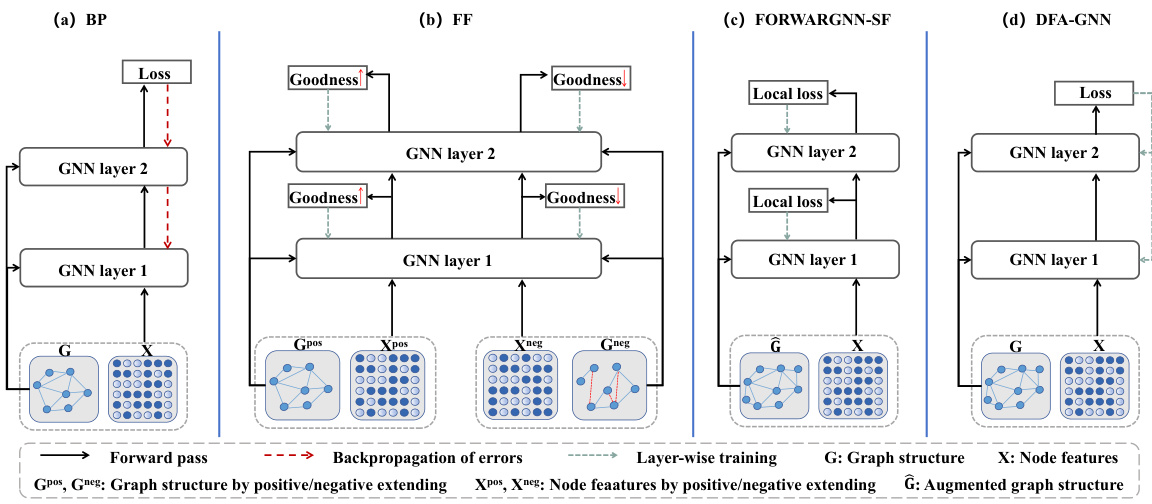
The figure illustrates four different training methods for graph neural networks (GNNs): Backpropagation (BP), Forward-Forward (FF), FORWARDGNN, and the proposed Direct Feedback Alignment-GNN (DFA-GNN). It visually compares the flow of information, including forward and backward passes, weight updates, and the handling of errors for each method. BP uses traditional backpropagation with a complete backward pass to adjust weights. FF uses two forward passes, one with positive and one with negative samples. FORWARDGNN uses layer-wise training with data augmentation. DFA-GNN, in contrast, leverages a direct feedback alignment mechanism, extending the principles of DFA to adapt to the unique structure of GNNs and the non-Euclidean nature of graph data, incorporating graph topology into feedback links. For semi-supervised learning, it includes a pseudo error generator to address the unavailability of true errors for all nodes.

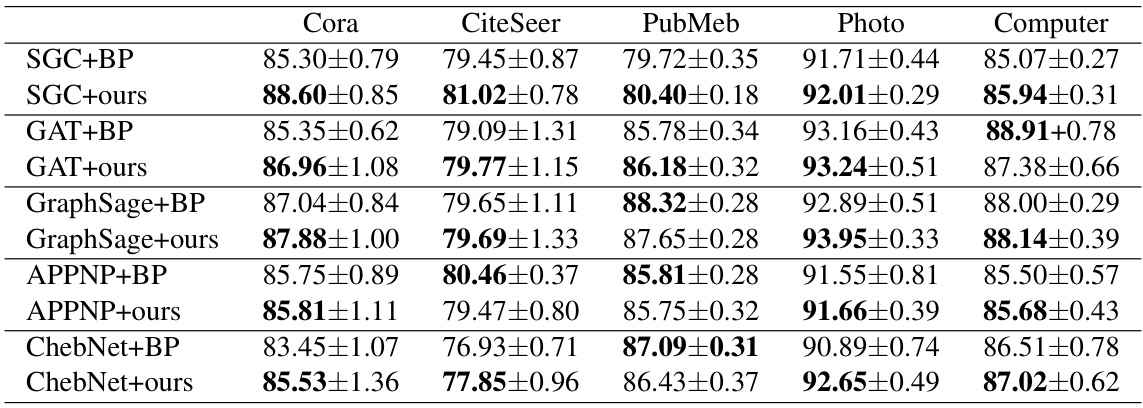
This table presents the mean accuracy and 95% confidence intervals achieved by various node classification methods on ten benchmark datasets. The methods compared include backpropagation (BP), PEPITA, CaFo (two versions), FF (two versions), FORWARDGNN-SF (SF), and the proposed DFA-GNN. The best performance on each dataset is highlighted in bold. This provides a quantitative comparison of the effectiveness of the proposed method against existing state-of-the-art and standard approaches.
In-depth insights#
DFA-GNN’s Design#
DFA-GNN cleverly adapts the principles of Direct Feedback Alignment (DFA) to the unique architecture of Graph Neural Networks (GNNs). The core innovation lies in incorporating graph topology information into the feedback links, moving beyond the limitations of DFA’s application to Euclidean data. This is achieved by integrating the adjacency matrix into the error feedback mechanism, enabling the method to effectively handle non-Euclidean characteristics of graph data. Furthermore, DFA-GNN addresses the challenge of semi-supervised learning by introducing a pseudo-error generator. This component strategically propagates residual errors from labeled nodes to unlabeled ones, providing feedback signals for training on the entire graph, even in the absence of complete ground truth labels. This design is crucial for enhancing the model’s performance and robustness in scenarios with limited labeled data. The combination of topology-aware feedback and pseudo-error generation allows DFA-GNN to learn effectively and efficiently from graph data, achieving excellent performance and biological plausibility.
Pseudo-error Gen.#
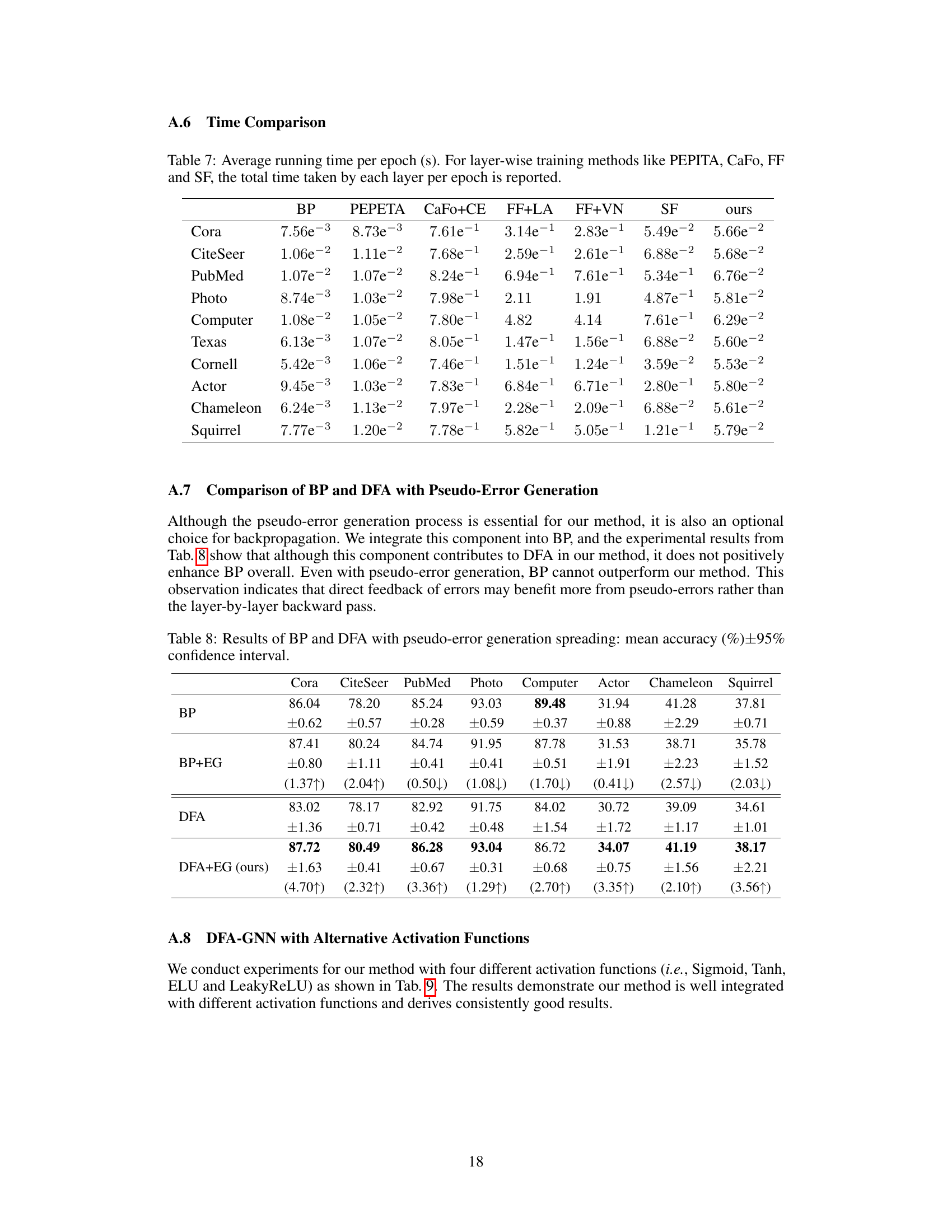
The ‘Pseudo-error Gen.’ section tackles a critical challenge in adapting Direct Feedback Alignment (DFA) to Graph Neural Networks (GNNs) for semi-supervised learning. The core problem is the lack of ground truth labels for all nodes in the graph, hindering the calculation of accurate error signals needed for training. To address this, the authors ingeniously devise a pseudo-error generator. This mechanism leverages the labeled nodes’ residual errors, spreading them to the unlabeled nodes via a process inspired by label propagation techniques. This approach cleverly addresses the non-i.i.d. nature of graph data, avoiding the pitfalls of directly applying DFA designed for Euclidean data to the non-Euclidean graph domain. The effectiveness of the pseudo-error generator is demonstrated empirically, showing that using these propagated errors significantly improves the performance of DFA-GNN, especially in semi-supervised settings. The inherent cleverness lies in the ability to transfer the scarce error information from labeled nodes to inform the learning process for unlabeled ones, bridging the gap and enhancing the GNN’s capacity to generalize from limited supervision.
Convergence Proof#
A rigorous convergence proof for a novel training algorithm, like the DFA-GNN presented in this hypothetical research paper, would be a significant contribution. The proof should establish that the algorithm’s parameter updates reliably lead to a reduction in loss and ultimately, convergence to an optimal or near-optimal solution. Key aspects to address would include showing the algorithm’s stability, addressing the non-Euclidean nature of graph data, and handling the challenges posed by semi-supervised learning. Demonstrating that the random feedback matrices in DFA-GNN do not hinder convergence, but instead facilitate efficient learning, would be crucial. The proof might leverage techniques from optimization theory, graph theory, and potentially probabilistic analysis, to show that the error decreases monotonically or within a specific tolerance. A key element is how the pseudo-error generation mechanism influences convergence and whether the proof establishes error bounds or convergence rates. The overall impact of the proof would strengthen the paper’s claims and its impact in the machine learning community by providing strong theoretical backing for the practical effectiveness of DFA-GNN.
Robustness Analysis#
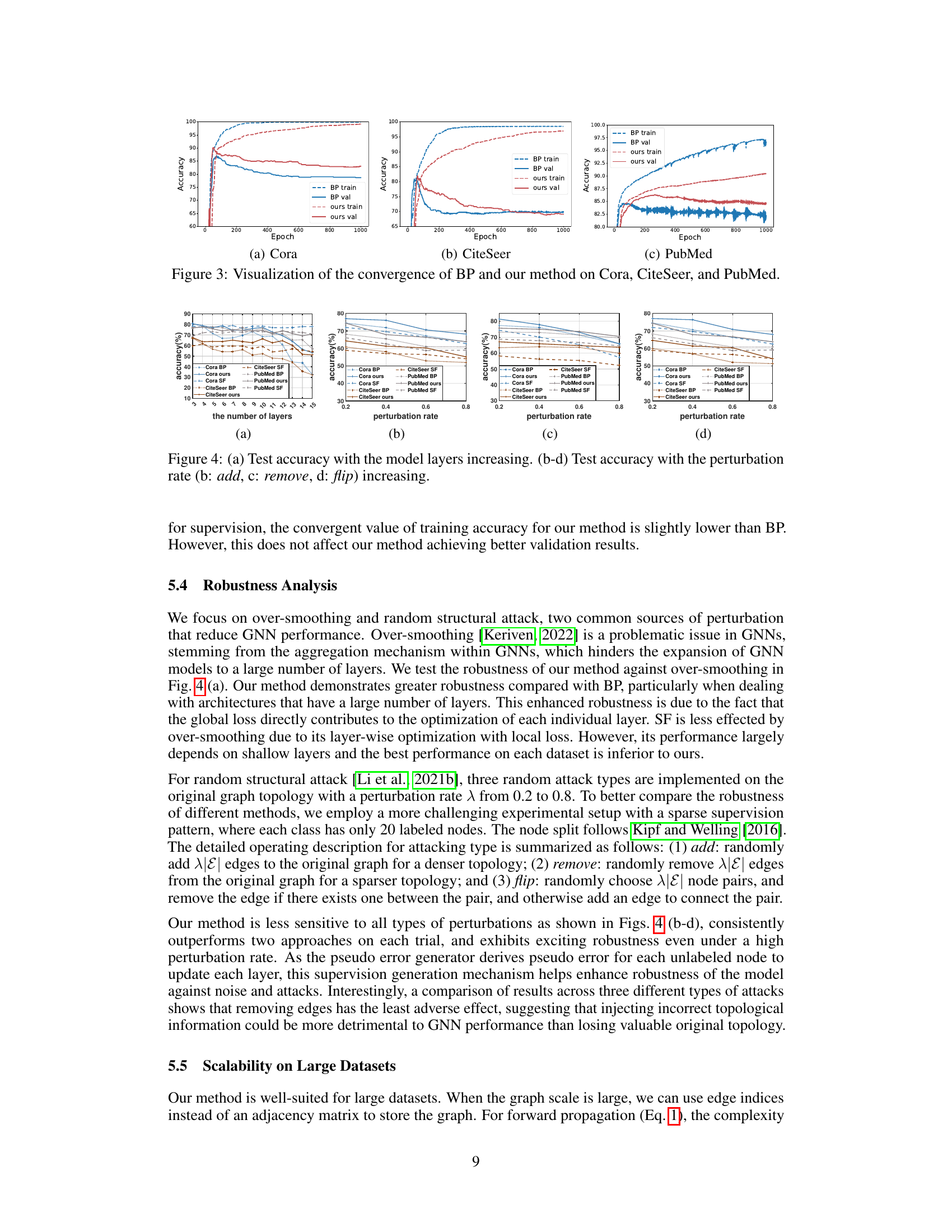
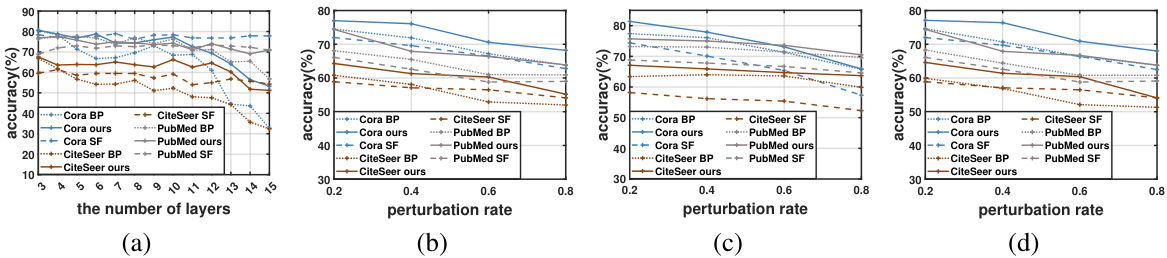
The robustness analysis section of a research paper is crucial for evaluating the reliability and generalizability of the proposed model. It should thoroughly assess the model’s performance under various challenging conditions, such as noise, adversarial attacks, or variations in data distribution. A strong robustness analysis would present the model’s resilience to over-smoothing by varying the number of layers, showing consistent performance regardless of depth. Furthermore, it should evaluate the impact of random structural attacks, such as edge removal or addition, on the model’s accuracy, demonstrating the model’s stability against data corruption. The inclusion of detailed quantitative results with appropriate error metrics is essential. Statistical significance tests should be used to support claims about the robustness of the model. Finally, the analysis should consider the specific characteristics of the data and task, potentially drawing comparisons with other models and methods to offer a comprehensive evaluation of the model’s real-world applicability.
Scalability & Limits#
A crucial aspect of any machine learning model is its scalability. The paper’s approach to graph neural networks (GNNs) shows promise in terms of scalability by cleverly using edge indices instead of adjacency matrices for large graphs. This significantly reduces computational complexity, a major improvement over traditional methods. However, the paper doesn’t explicitly discuss limitations to scalability, such as memory constraints for extremely large graphs, or the potential for computational bottlenecks during error propagation. Addressing these potential limits through further analysis and possibly optimized algorithms is vital for real-world applications. Exploring the trade-off between accuracy and efficiency at different scales would also provide valuable insights into the practical boundaries of the DFA-GNN approach. Finally, the impact of graph sparsity and density on scalability should be investigated, as the method’s efficiency could potentially vary depending on graph topology and structure.
More visual insights#
More on figures

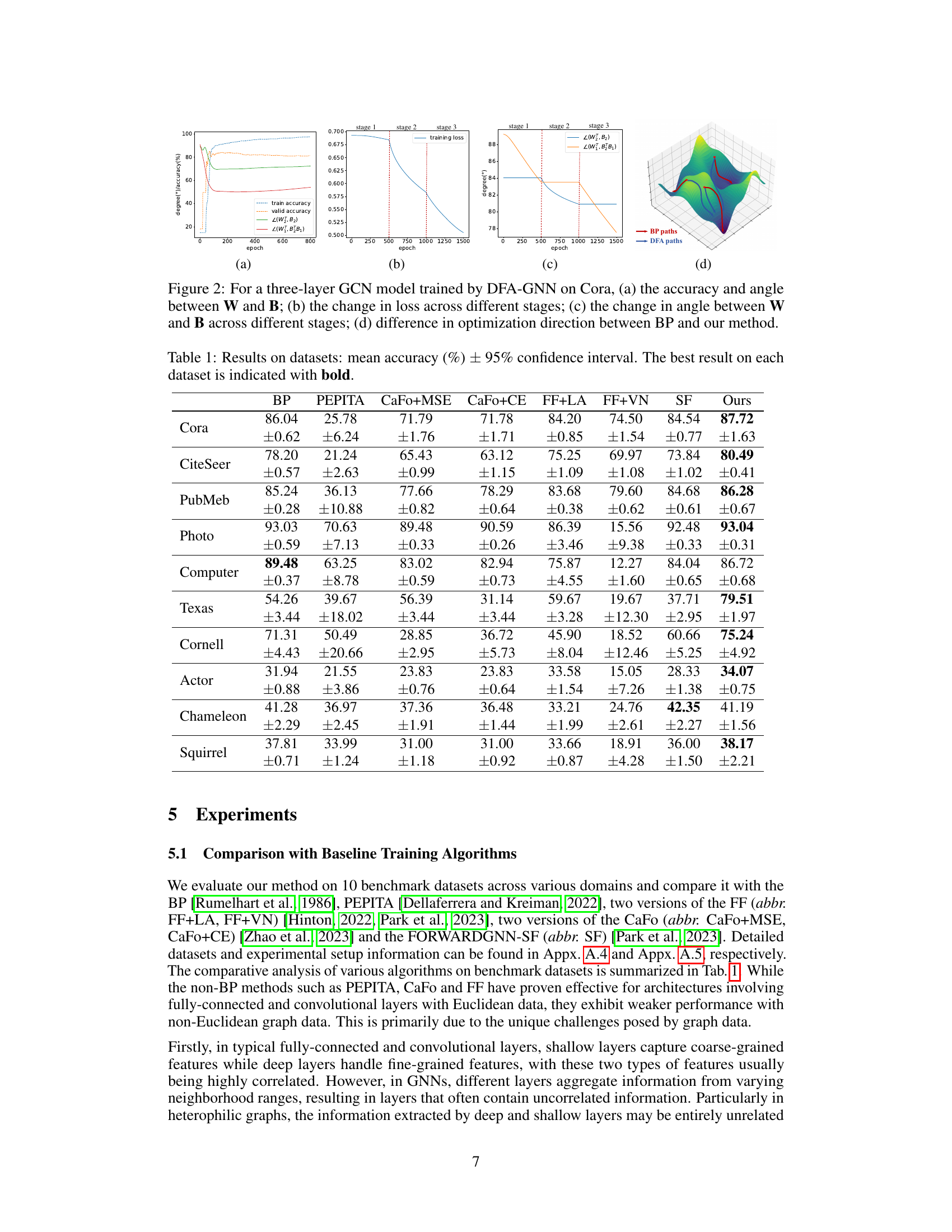
This figure visualizes various aspects of the DFA-GNN training process on the Cora dataset using a three-layer GCN model. Subfigure (a) shows the training accuracy and the angle between the forward weights (W) and feedback weights (B) over training epochs, illustrating the alignment between them. Subfigure (b) demonstrates the training loss across three distinct stages of training: training layers 1 and 2 while freezing layer 3, freezing layers 1 and 2 while training layer 3, and training layers 1 and 2 while freezing layer 3. Subfigure (c) presents the dynamic changes in the angle between W and B across these training stages. Finally, subfigure (d) provides a 3D visualization of the optimization direction differences between the traditional backpropagation (BP) and the proposed DFA-GNN methods, highlighting the distinct optimization paths taken by each approach.
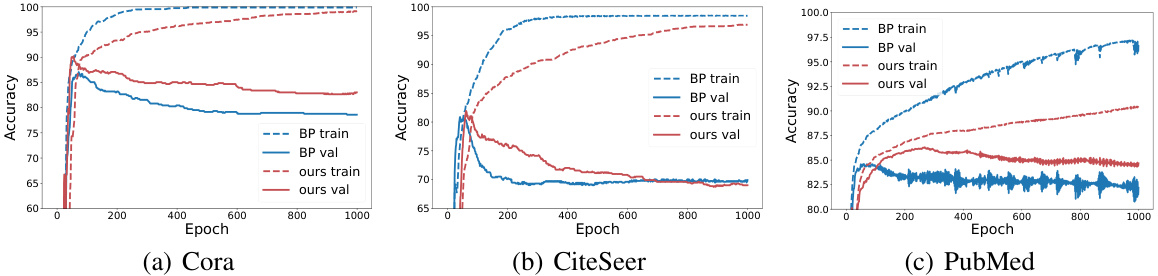
This figure visualizes the training and validation accuracy convergence for both backpropagation (BP) and the proposed DFA-GNN method across three datasets: Cora, CiteSeer, and PubMed. The plots show the accuracy over training epochs. It demonstrates that while DFA-GNN shows a slightly slower convergence rate in training accuracy compared to BP, it achieves superior validation accuracy, indicating less overfitting.
This figure visualizes the training process of DFA-GNN on the Cora dataset using a three-layer GCN model. Panel (a) shows the relationship between training accuracy and the angle between the forward weights (W) and feedback weights (B) during training. Panel (b) displays the changes in training loss across three training stages: stage 1 (layers 1 and 2 trained, layer 3 frozen), stage 2 (layer 3 trained, layers 1 and 2 frozen), and stage 3 (layers 1 and 2 trained, layer 3 frozen). Panel (c) illustrates the change in the angle between W and B across these same training stages. Finally, panel (d) provides a 3D visualization contrasting the optimization direction taken by DFA-GNN against traditional BP.
More on tables

This table presents the ablation study of the proposed DFA-GNN model. It shows the impact of removing the pseudo-error generator (EG) and node filter (NF) components on the model’s performance across six different datasets. Each row represents a different configuration (EG and NF either included or removed). The performance is measured by mean accuracy ± 95% confidence interval, allowing for a comparison of the model’s robustness under different settings and datasets.

This table presents the performance comparison of different algorithms on three large-scale datasets: Flickr, Reddit, and ogbn-arxiv. The results show the mean accuracy achieved by each algorithm. OOM indicates that the algorithm ran out of memory and could not complete the task on the dataset.
This table presents the mean accuracy and 95% confidence intervals achieved by different node classification methods on ten benchmark datasets. The methods compared include backpropagation (BP), PEPITA, CaFo (two versions), FF (two versions), SF, and the proposed DFA-GNN. The best-performing method for each dataset is highlighted in bold, showcasing the relative performance of each algorithm across diverse graph datasets.

This table presents the mean accuracy and 95% confidence intervals achieved by different methods (BP, PEPITA, CaFo+MSE, CaFo+CE, FF+LA, FF+VN, SF, and the proposed DFA-GNN) on ten benchmark datasets for node classification. The best performing method for each dataset is highlighted in bold. This provides a comparison of the performance of the proposed DFA-GNN method against existing baseline methods for semi-supervised node classification on graph data.
This table presents the results of the proposed DFA-GNN model and several baseline methods on ten benchmark datasets. The accuracy of each method is reported as the mean accuracy across ten random splits, along with the 95% confidence interval. The best performing method for each dataset is highlighted in bold. This allows for a direct comparison of the proposed method against several state-of-the-art baselines, demonstrating its effectiveness.

This table presents the results of the proposed DFA-GNN method and several baseline methods on ten different benchmark datasets. The results are reported as mean accuracy with a 95% confidence interval. The best result achieved for each dataset is highlighted in bold. The table allows for a comparison of the performance of DFA-GNN against existing backpropagation (BP) and other non-BP methods across various types of graph datasets.

This table presents the mean accuracy and 95% confidence intervals achieved by various methods (BP, PEPITA, CaFo+MSE, CaFo+CE, FF+LA, FF+VN, SF, and the proposed DFA-GNN) on ten different benchmark datasets. The best performing method for each dataset is highlighted in bold, providing a clear comparison of the proposed method against existing baselines.

This table presents the mean accuracy and 95% confidence intervals achieved by various methods on ten different benchmark datasets. The methods compared include backpropagation (BP), PEPITA, CaFo, FF, SF, and the proposed DFA-GNN. The best performing method for each dataset is highlighted in bold, enabling easy comparison of the different approaches across a range of graph datasets.
Full paper#