↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Reinforcement learning (RL) struggles in partially observable environments (POMDPs) due to the difficulty of modeling the belief state. A common workaround is using an agent state that summarizes past observations and actions. However, traditional RL algorithms assume a stationary policy, which is suboptimal since agent states generally don’t follow the Markov property. This is an important issue because many real-world scenarios are partially observable. This paper addresses these challenges.
The proposed solution, PASQL (Periodic Agent-state based Q-learning), learns periodic policies instead of stationary ones. This is theoretically justified by combining Markov chain theory with stochastic approximation. PASQL is shown to converge to a periodic policy and its sub-optimality gap is analyzed. Numerical experiments showcase PASQL’s superior performance compared to standard agent-state based Q-learning in a non-trivial POMDP.
Key Takeaways#
Why does it matter?#
This paper is crucial because it tackles the limitations of existing reinforcement learning algorithms in handling partially observable environments. By introducing periodic policies, it offers a novel approach to enhance performance, particularly in scenarios where the agent’s internal state doesn’t fully capture the environment’s dynamics. The findings provide a new direction for researchers and open up avenues for developing improved RL methods and a deeper understanding of non-stationary policies in real-world applications.
Visual Insights#
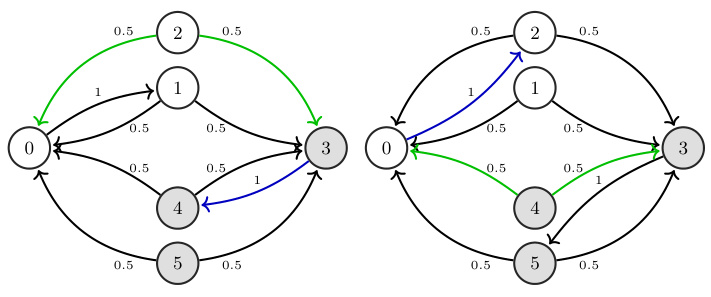
This figure shows two diagrams illustrating the dynamics of a POMDP under two different actions (0 and 1). The states are represented as nodes, and the transitions between states are represented by edges. The colors of the nodes indicate the observations associated with each state (white for 0 and grey for 1). The colors of the edges represent rewards: green for +1 and blue for +0.5. Each diagram shows the probability of transitioning to another state given the current state and the action taken. This is a simplified representation of the POMDP that helps in demonstrating the behavior and performance of different reinforcement learning algorithms.

This table presents the performance of periodic policies with different periods (L). The optimal performance J*L for each period L is shown. The performance was obtained by conducting a brute-force search over all deterministic periodic policies with a period up to 10 in a specific example POMDP. It highlights how the performance of periodic policies can outperform stationary policies in certain partially observable Markov decision processes (POMDPs) and illustrates the relationship between period length and performance.
In-depth insights#
POMDP Q-Learning#
Partially Observable Markov Decision Processes (POMDPs) present a significant challenge in reinforcement learning due to their inherent uncertainty. Standard Q-learning, designed for fully observable Markov Decision Processes (MDPs), struggles to directly handle POMDPs because the belief state (probability distribution over hidden states) is typically high-dimensional and non-Markovian. Agent-state based Q-learning emerges as a practical approach, representing the agent’s uncertainty using a recursively updated, model-free function of past observations and actions, thereby creating a Markov approximation for learning. This approach faces limitations, however; the crucial issue is that the agent’s representation may not accurately capture the environment’s true underlying state distribution. Standard Q-learning algorithms often learn stationary policies which are suboptimal in agent-state POMDPs because the Markov property is not guaranteed. This paper introduces PASQL (Periodic Agent-State based Q-Learning), addressing these issues by learning periodic policies. By leveraging periodicity, PASQL can model non-stationary behavior that can improve performance compared to traditional methods. Rigorous analysis is included to demonstrate convergence and quantify the approximation error.
Agent-State Models#
Agent-state models offer a powerful approach to reinforcement learning in Partially Observable Markov Decision Processes (POMDPs) by approximating the belief state. Instead of tracking the full belief state, which is computationally expensive and often intractable, agent-state models use a compact representation of the agent’s history, such as stacked frames or recurrent neural networks. This model-free approach makes them applicable to real-world scenarios where the system’s dynamics are unknown. However, a key limitation of agent-state models is that they typically violate the Markov property, meaning that the future state is not solely dependent on the current agent state and action but also on the past history. This non-Markovian nature complicates the theoretical analysis and can lead to suboptimal policies. While standard reinforcement learning algorithms assume a Markov decision process, techniques like periodic agent-state Q-learning address this by learning periodic policies. This approach leverages the inherent non-stationarity of agent-state models to improve performance, showing that they can outperform stationary policies in many cases. Further research is needed to improve the expressiveness of agent-state representations and to develop more sophisticated learning algorithms for POMDPs.
Periodic Policies#
The concept of “Periodic Policies” introduces non-stationarity into reinforcement learning, particularly beneficial for Partially Observable Markov Decision Processes (POMDPs). Unlike stationary policies that remain consistent, periodic policies systematically alternate between a set of predefined policies, creating a cyclical pattern. This approach leverages the fact that agent states in POMDPs, unlike true Markov states, don’t always possess the Markov property, rendering stationary policies suboptimal. By learning a periodic policy, the agent can adapt its behavior to the non-stationarity inherent in the agent’s state transitions and effectively learn a better policy than a solely stationary strategy. The periodic nature allows for a finite representation of a non-stationary policy, making it computationally tractable while capturing temporal dependencies often missed by standard algorithms. However, the effectiveness depends heavily on the choice of behavioral policy during learning and the period length, highlighting that finding optimal periodic policies remains a challenge that requires more exploration.
PASQL Algorithm#
The core of the research paper revolves around the PASQL (Periodic Agent-State based Q-learning) algorithm, a novel approach to reinforcement learning in Partially Observable Markov Decision Processes (POMDPs). PASQL addresses the limitations of standard Q-learning in POMDPs, which often struggle with the non-Markovian nature of agent states. By incorporating periodicity into the learning process, PASQL learns policies that are not stationary, thereby potentially achieving improved performance. The algorithm rigorously leverages periodic Markov chains and stochastic approximation, providing a theoretically sound framework for convergence analysis. A key contribution is the proof of convergence to a cyclic limit, and the subsequent characterization of the approximation error. This theoretical foundation is bolstered by numerical experiments demonstrating PASQL’s ability to outperform traditional, stationary approaches. The algorithm’s effectiveness is contingent upon careful selection of a suitable periodic behavior policy, highlighting a crucial trade-off between expressiveness and the computational cost of maintaining multiple Q-functions. Overall, PASQL presents a significant advance in tackling POMDPs by offering a principled method for harnessing the power of non-stationarity through periodic policies.
Convergence Analysis#
A rigorous convergence analysis is crucial for establishing the reliability and trustworthiness of any machine learning algorithm. In the context of reinforcement learning, especially for partially observable Markov decision processes (POMDPs), demonstrating convergence is challenging due to the inherent complexities of the problem. A key aspect often analyzed is the convergence of the Q-function, a central component in Q-learning. For POMDPs, the use of an agent state, a model-free representation of the observation history, adds another layer of complexity. The analysis must address the non-Markovian nature of the agent state, as this violates the standard assumptions of many convergence proofs. Researchers often explore stochastic approximation techniques to handle the inherent randomness and non-stationarity. Establishing convergence to a cyclic limit for periodic policies is a significant achievement, proving that the proposed algorithm learns effective and reliable strategies in POMDPs. The analysis should ideally characterize the rate of convergence, identify sufficient conditions, and possibly provide bounds on the approximation error. Quantifying the sub-optimality gap helps determine how close the learned policy is to the optimal solution, offering valuable insights into the algorithm’s performance and limitations. A comprehensive convergence analysis will greatly enhance the paper’s contribution, providing crucial insights into the algorithm’s efficacy and theoretical foundation.
More visual insights#
More on figures
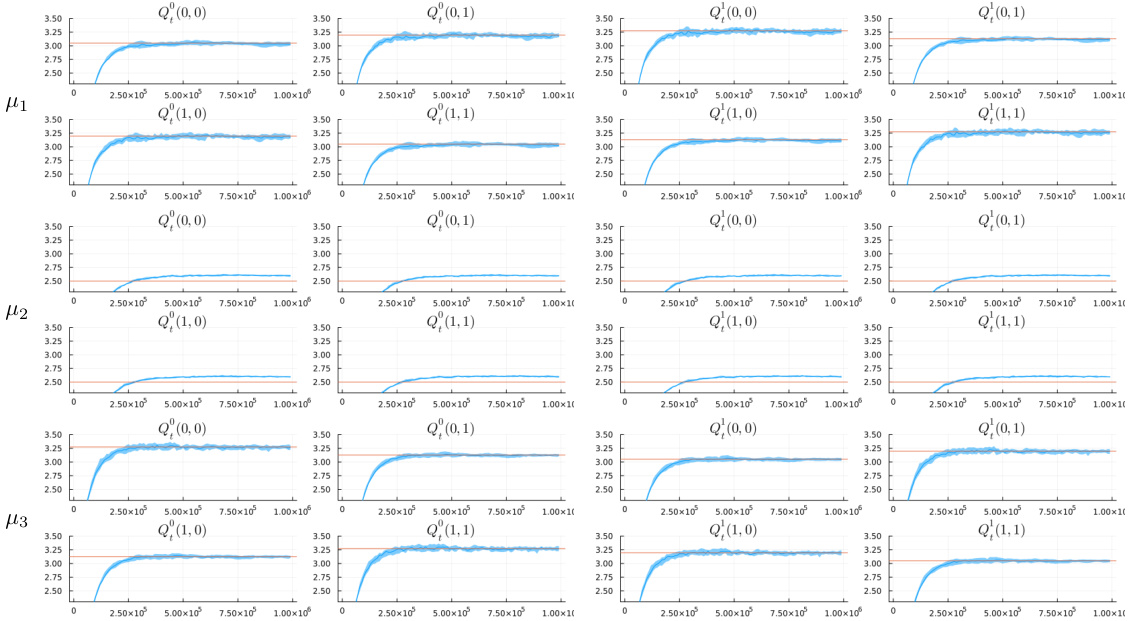
This figure shows the results of a numerical experiment on the convergence of PASQL with different behavioral policies. The plots show the evolution of the Q-values for different state-action pairs over time for three different behavioral policies (μ1, μ2, and μ3). The blue lines represent the actual Q-values learned by PASQL, while the red lines represent the theoretical limits predicted by Theorem 1. The experiment demonstrates the convergence of PASQL to its theoretical limit and the effect of different behavioral policies on the learning process.

This figure shows a T-shaped grid world used as an example in the paper. The agent starts at ’s’ and must learn which goal state (G1 or G2) is the correct one. The agent can only observe its location in the corridor (gray cells) or its location at either T, G1, or G2. The agent receives a reward of +1 for reaching the correct goal state and -1 for the incorrect one. The example highlights the difference between memory and periodic policies in solving the problem.

This figure shows the results of the PASQL algorithm for three different behavioral policies (μ1, μ2, μ3). The blue lines represent the actual iterates of the PASQL algorithm, while the red lines represent the theoretical limit predicted by Theorem 1. The plots show the convergence of the Q-function for each action-state pair ((0,0), (0,1), (1,0), (1,1)) across iterations. The figure illustrates that PASQL converges to the theoretical limit, and that the limiting value depends on the behavioral policy used.

This figure shows a POMDP model used in numerical experiments. The model has six states (0-5), two actions (0 and 1), and two observations (0 and 1). States 0, 1, and 2 have observation 0, and states 3, 4, and 5 have observation 1. Transitions are represented by edges, with green edges indicating a reward of +1, blue edges +0.5, and other transitions having no reward. The figure is divided into two parts: (a) dynamics under action 0 and (b) dynamics under action 1, showing how the state transitions differ based on the chosen action.
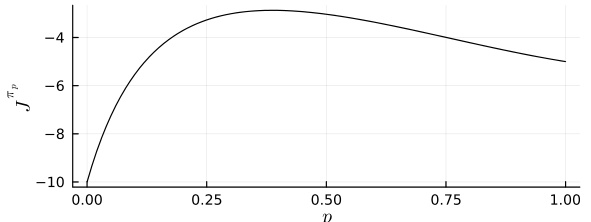
The figure shows the performance of stationary stochastic policies for different values of p, which is the probability of choosing action 1. The x-axis represents p, and the y-axis represents the performance Jπp. The curve shows that the optimal performance is achieved by a stochastic policy with p ≈ 0.39.

This figure illustrates a T-shaped grid world environment used in Example 4 of the paper to demonstrate the difference between stationary policies with memory augmentation and periodic policies. The agent starts at state ’s’, must navigate a long corridor of 2n cells to reach a decision point ‘T’. At ‘T’, the agent chooses to go up to G1 or down to G2. The reward is +1 for the correct goal and -1 otherwise. The observation space is limited, making the problem partially observable. This example highlights the limitations of policies with limited memory and how periodic policies can achieve optimal performance with a small number of parameters.
More on tables
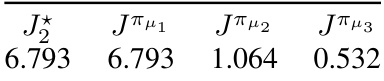
This table presents the performance of periodic policies obtained by using three different behavioral policies (µ1, µ2, µ3) in PASQL. The optimal performance (J*2) achievable by a period-2 policy is also shown for comparison. The results demonstrate the impact of the behavioral policy on the performance of the resulting periodic policy. Policy µ1 achieves the optimal performance, while µ2 and µ3 show significantly lower performance.
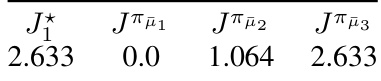
This table presents the performance comparison between the optimal stationary policy and the greedy policies obtained from ASQL under different behavioral policies. The optimal performance is calculated by a brute-force search across all possible stationary deterministic agent-state policies. The performance of the greedy policies from ASQL are calculated via policy evaluation over all the states and agent states.

This table presents the performance of converged periodic policies (PASQL) with period L=2 and three different behavioral policies (μ₁, μ₂, μ₃). It compares the performance (J) of these policies to the optimal performance (J*) achievable by a period-2 deterministic agent-state policy found through a brute-force search. The results show the impact of the behavioral policy on the performance of the learned periodic policy.
Full paper#



















