↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
User-level differential privacy (DP) in stochastic convex optimization (SCO) is crucial for protecting user data in machine learning, but existing algorithms are slow and make restrictive assumptions. These algorithms are impractical for many large-scale machine learning applications due to limitations in their runtime and accuracy. They often require restrictive assumptions about the smoothness of the loss function or the relationship between the number of users and the dimensionality of the data. This work directly addresses these shortcomings.
The paper proposes novel user-level DP algorithms with state-of-the-art excess risk and runtime guarantees. It introduces a linear-time algorithm with optimal excess risk under mild assumptions. Two other algorithms are presented, one for smooth and one for non-smooth loss functions, that also achieve optimal excess risk with substantially fewer gradient computations than previously possible. These algorithms don’t require the number of users to grow polynomially with the parameter space dimension, making them applicable to a wider range of real-world scenarios.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in differential privacy and machine learning because it presents significantly faster algorithms for user-level private stochastic convex optimization, a critical area for building privacy-preserving machine learning models. It addresses the limitations of previous algorithms by offering improved runtime and excess risk guarantees without stringent assumptions. This opens new avenues for research, allowing for more efficient and practical applications of differential privacy in large-scale machine learning.
Visual Insights#

This table compares the gradient complexities and assumptions of different algorithms for user-level differentially private stochastic convex optimization (DP-SCO). It shows that the proposed algorithms (Algorithm 3) significantly improve upon previous state-of-the-art methods in terms of computational efficiency (gradient complexity) while relaxing restrictive assumptions.
In-depth insights#
User-Level DP SCO#
User-Level Differential Privacy Stochastic Convex Optimization (DP-SCO) presents a unique challenge in balancing privacy with utility. The core problem involves protecting the privacy of each user’s entire dataset, not just individual data points. This contrasts with item-level DP, which offers weaker privacy guarantees when users provide numerous data points. Existing algorithms often suffer from restrictive assumptions, like requirements on smoothness parameters or the number of users, leading to impractical runtimes. The focus on faster and more efficient algorithms that avoid these restrictive assumptions is key. Efficient algorithms with optimal excess risk are a significant focus, achieving this without relying on strong conditions represents a major advance in the field. The exploration of linear-time algorithms adds another important layer to the investigation, aiming to reduce computational cost without compromising privacy guarantees. Overall, research in user-level DP-SCO strives to make differentially private machine learning more practical for real-world large-scale applications.
Linear-Time Algo#
The pursuit of a linear-time algorithm for user-level differentially private stochastic convex optimization (SCO) represents a significant challenge and a major focus of the research. A linear-time algorithm offers a substantial improvement over existing methods with suboptimal runtime, making private SCO feasible for large-scale applications. The core difficulty lies in balancing the need for computational efficiency with the strong privacy guarantees required by user-level differential privacy. Existing algorithms either make restrictive assumptions about the smoothness of the loss function or require a prohibitively large number of gradient computations. A linear-time algorithm that overcomes these limitations would be a breakthrough, potentially opening up new avenues for practical applications of private machine learning. This research contributes to addressing this challenge by proposing a new algorithm that significantly improves runtime while maintaining state-of-the-art accuracy under mild assumptions, although achieving fully optimal linear-time performance remains an open problem, suggesting further avenues for exploration and improvement.
Optimal Algo#
An optimal algorithm, in the context of user-level private stochastic convex optimization, would achieve the best possible balance between privacy preservation and accuracy. It would achieve the theoretical lower bound on excess risk, meaning it performs as well as is theoretically possible given the privacy constraints. Developing such an algorithm is challenging because user-level differential privacy is a strong privacy guarantee that restricts the amount of information that can be released. The algorithm would likely employ sophisticated techniques, such as noise addition and advanced composition methods, to ensure privacy. Its efficiency would be key—an algorithm with high computational cost is impractical for large-scale machine learning applications. Therefore, it’s crucial that any ‘Optimal Algo’ design incorporates runtime considerations, striving for an efficient implementation with low gradient complexity.
Non-Smooth Loss#
The treatment of non-smooth loss functions in private stochastic convex optimization (SCO) presents unique challenges. Standard gradient-based methods fail due to the discontinuity or lack of differentiability inherent in these losses. Therefore, techniques such as randomized smoothing are often employed to approximate the non-smooth loss with a smooth one, allowing for the application of gradient-based DP-SCO algorithms. However, this approximation introduces error, affecting the accuracy of the results and requiring careful analysis of the resulting excess risk. The trade-off between the level of smoothing (which influences the smoothness parameter and computational complexity) and the resulting error needs careful consideration. Algorithms designed specifically for non-smooth losses might offer improved efficiency and accuracy compared to applying smoothing techniques, and thus represent an active area of research in DP-SCO.
Future Research#
The paper’s conclusion alludes to exciting avenues for future research. Extending the linear-time algorithm to achieve optimal excess risk under milder smoothness assumptions is a significant goal. Further investigation into the limitations of (ε,δ)-DP, and exploration of pure ε-DP for user-level SCO, are crucial. Applying the techniques to federated learning settings, where communication constraints exist, presents another challenge. Finally, addressing the practical implications of applying these algorithms to non-convex problems, prevalent in deep learning, represents a considerable area of future work. These advancements could lead to more robust and privacy-preserving machine learning systems.
More visual insights#
More on tables
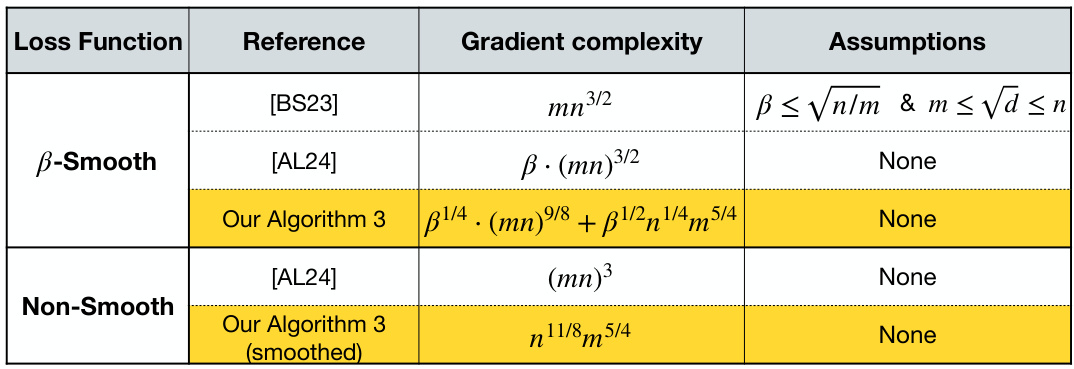
This table compares the gradient complexities and assumptions of different algorithms for user-level differentially private stochastic convex optimization (DP SCO). It shows that the proposed Algorithm 3 achieves optimal gradient complexity under less restrictive assumptions compared to prior state-of-the-art algorithms. The comparison is made for both smooth and non-smooth loss functions.

The table compares the gradient complexity and assumptions of different algorithms for user-level differentially private stochastic convex optimization (DP-SCO). It shows that the proposed algorithms (Algorithm 3) achieve optimal excess risk with lower gradient complexity compared to existing methods, and without requiring restrictive assumptions on the smoothness parameter or the number of users.
Full paper#