Is Score Matching Suitable for Estimating Point Processes?

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it addresses the limitations of existing score matching estimators for point processes, which are widely used in various fields. By introducing the weighted score matching estimator and proving its consistency, this work provides a reliable and efficient method for parameter estimation in these complex models, opening new avenues for research and improving the accuracy of applications in diverse domains.

Visual Insights

#

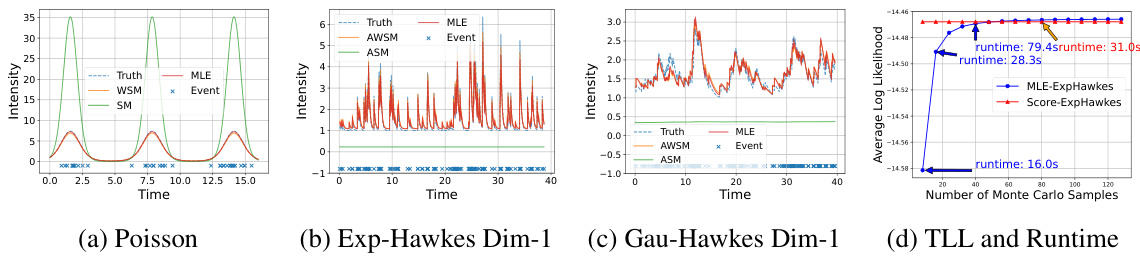
This figure compares the performance of MLE, (A)SM, and (A)WSM in estimating the intensity functions of three different point processes: Poisson, Exponential Hawkes, and Gaussian Hawkes. Subfigures (a), (b), and (c) show the learned intensity functions for each method, demonstrating that (A)WSM and MLE produce similar and accurate results that closely match the ground truth, whereas (A)SM performs poorly. Subfigure (d) illustrates the trade-off between accuracy and computational cost (runtime) for MLE and (A)WSM, highlighting the computational advantage of (A)WSM, especially when using a limited number of Monte Carlo samples for numerical integration.

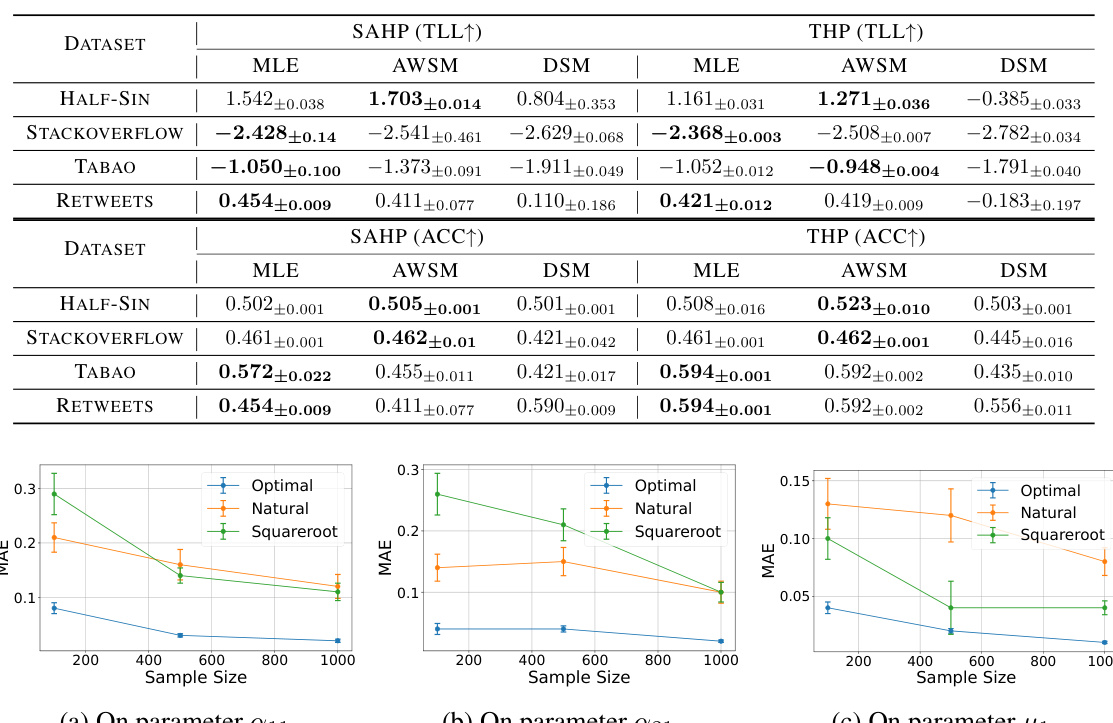
This table presents the Mean Absolute Error (MAE) for three different parameter estimation methods (MLE, (A)SM, and (A)WSM) applied to synthetic datasets of Poisson and Hawkes processes. The MAE is a measure of the accuracy of the estimations. Lower MAE values indicate more accurate estimations. The table highlights the superior performance of the proposed (A)WSM method, especially when compared to the (A)SM method, which demonstrates its limitations for general point processes.

In-depth insights

#

Score Matching Limits

#

The heading ‘Score Matching Limits’ suggests an examination of the inherent boundaries and shortcomings of score matching methods, particularly in the context of point process estimation. The discussion likely delves into scenarios where score matching fails to accurately estimate model parameters. A core limitation is the reliance on implicit score matching, which necessitates specific regularity conditions often violated in complex point processes. This section likely demonstrates how such violations prevent the accurate estimation of model parameters, leading to unreliable results. The analysis might identify specific types of point processes (e.g., those with high dimensionality or complex intensity functions) where the limitations are particularly pronounced. The exploration of these limits is crucial for establishing the applicability and reliability of score matching in various settings and for guiding the development of improved or alternative estimation techniques. The findings could highlight the need for alternative methods (such as weighted score matching) and provide a framework for assessing the suitability of score matching for specific applications. Finally, it may explore the trade-offs between computational efficiency and estimation accuracy inherent in score matching approaches.

Weighted Score Match

#

Weighted score matching (WSM) addresses limitations of standard score matching (SM) in estimating point processes. Standard SM, while avoiding the intractable normalizing constant of maximum likelihood estimation, often fails for general point processes due to unmet regularity conditions. WSM overcomes this by introducing a weight function that strategically modifies the objective, eliminating problematic terms that arise near integration boundaries. This innovation allows consistent parameter estimation for a broader class of processes, as demonstrated theoretically and empirically. The introduction of this weight function is crucial as it allows for the control over the behavior of the objective function near integration limits, directly addressing the core deficiency of standard SM in the context of point processes. The theoretical analysis proves WSM’s consistency and establishes its convergence rate. Experiments validate its efficacy in recovering ground truth parameters on synthetic data and its comparability to maximum likelihood estimation (MLE) on real data, while highlighting the failure of standard SM in such scenarios. WSM thus represents a significant improvement in statistical modeling of point processes.

Hawkes Process ASM

#

Autoregressive Score Matching (ASM) applied to Hawkes processes presents a compelling approach to parameter estimation, sidestepping the computational burden of traditional maximum likelihood estimation (MLE) by avoiding the intractable intensity integral. However, the paper reveals a critical limitation: existing ASM formulations for Hawkes processes, while seemingly elegant, rely on implicit assumptions that are not generally valid for a wide range of processes. The core issue is the incompleteness of the implicit ASM objective function, arising from the transition from explicit to implicit SM which requires regularity conditions often unmet by general Hawkes processes. This leads to inaccurate parameter estimates in many practical scenarios. The authors highlight this fundamental flaw and propose a novel solution—a weighted ASM (AWSM) approach. AWSM introduces a weight function to eliminate problematic terms in the objective, thus enabling consistent and accurate parameter estimation for more general cases. The theoretical underpinning of AWSM, along with empirical results showcasing its superiority over existing methods, forms the central contribution of this work. The development of AWSM is a significant advancement in the field, broadening the applicability of score matching techniques in point process modeling.

Autoregressive WSM

#

Autoregressive Weighted Score Matching (AWSM) addresses limitations of existing score matching methods for estimating parameters in autoregressive point processes like Hawkes processes. Standard score matching struggles with the intractable intensity integral inherent in such models. AWSM overcomes this by introducing a weight function that strategically eliminates problematic boundary terms during the integration-by-parts step commonly used to derive an implicit objective function. This weight function ensures the estimator’s consistency and provides a convergence rate. The theoretical elegance is complemented by empirical results demonstrating AWSM’s accuracy in parameter recovery on both synthetic and real-world datasets. AWSM’s ability to handle complex, autoregressive structures represents a significant advancement, surpassing the performance of previous score matching techniques while offering comparable accuracy to computationally expensive maximum likelihood estimation (MLE). The method also demonstrates superior computational efficiency compared to MLE in high-dimensional scenarios.

Future Work: Deep Models

#

Future research directions involving deep learning models for point process estimation are exciting. Extending weighted score matching to deep architectures would be a significant advancement, potentially addressing the limitations of existing methods in handling complex dependencies and high dimensionality. This could involve exploring novel architectures specifically designed for temporal data or incorporating attention mechanisms to capture long-range interactions. Furthermore, investigating the theoretical properties of deep weighted score matching estimators is crucial to ensure consistency and convergence. This requires developing new theoretical tools tailored to deep learning models and complex point process structures. Finally, applying these enhanced techniques to challenging real-world datasets across diverse domains like finance, neuroscience, and social networks will allow for a thorough assessment of their practical capabilities and pave the way for developing new insights and applications. Focus should also be given to the development of efficient training algorithms that scale well with large datasets, as training deep models can be computationally expensive.

More visual insights

#

More on figures

This figure compares the performance of three methods: Maximum Likelihood Estimation (MLE), Autoregressive Score Matching (ASM), and Autoregressive Weighted Score Matching (AWSM) for estimating the intensity functions of three types of point processes: Poisson, Exponential Hawkes, and Gaussian Hawkes. The results demonstrate that MLE and AWSM accurately estimate the intensity functions, closely matching the ground truth, while ASM significantly deviates. The subfigure (d) further illustrates the computational advantage of AWSM over MLE by comparing their test log-likelihood and runtime against the number of Monte Carlo samples used for numerical integration in MLE.

This figure compares the performance of three methods (MLE, (A)SM, and (A)WSM) for estimating the intensity functions of three different point processes: Poisson, Exponential Hawkes, and Gaussian Hawkes. The plots (a), (b), and (c) show the learned intensity functions for the first dimension of the bivariate processes, illustrating that MLE and (A)WSM accurately capture the ground truth while (A)SM fails. Plot (d) shows the test log-likelihood (TLL) and runtime of (A)WSM and MLE, demonstrating that AWSM offers computational advantages compared to MLE.

More on tables

This table shows the mean absolute error (MAE) for three different parameter estimation methods (MLE, (A)SM, and (A)WSM) on synthetic datasets. The datasets include Poisson, Exponential Hawkes, and Gaussian Hawkes processes. The MAE is a measure of how accurately each method estimates the model parameters. The table highlights the superior performance of (A)WSM, particularly in the 2-variate cases, compared to (A)SM and the expected good performance of MLE.

This table presents the Mean Absolute Error (MAE) for estimating parameters of two types of bivariate Hawkes processes using three different methods: Maximum Likelihood Estimation (MLE), (Autoregressive) Score Matching ((A)SM), and (Autoregressive) Weighted Score Matching ((A)WSM). The results show the MAE for each parameter (α12, α21, α22, μ2) of the exponential and Gaussian Hawkes processes. It demonstrates the performance comparison of the three estimation methods on a synthetic dataset, highlighting the accuracy of (A)WSM compared to MLE and the significant errors produced by (A)SM.

This table presents the hyperparameters used for the experiments comparing different methods (MLE, AWSM, and DSM) on four datasets using two different models (SAHP and THP). It details the number of epochs used for training each model with each method, the balancing coefficient (αAWSM) for the AWSM method, whether data truncation was performed (TRUNC), and the hyperparameters for the DSM method (αDSM and σDSM).

Full paper

#