↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Higher-order Graph Neural Networks (GNNs) aim to improve upon standard GNNs by considering not just individual nodes, but also interactions between groups of nodes, such as cycles or functional groups in molecules. However, creating such higher-order GNNs requires careful handling of automorphism group equivariance. This is computationally complex as it demands finding appropriate operations for each group, making it difficult to scale. This paper tackles this problem by introducing a new algorithm called “Schur Nets”.
Schur Nets cleverly sidesteps the computationally expensive task of explicitly finding automorphism groups. It utilizes spectral graph theory, which is much more efficient, to directly construct a basis for equivariant operations from the graph Laplacian. This approach is shown to improve higher-order GNN performance, particularly in tasks like molecular property prediction, where local structure is vital. The key contribution is an efficient and scalable algorithm for building automorphism equivariant higher-order GNNs.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on graph neural networks (GNNs) because it introduces a novel and efficient method to enhance the expressive power of GNNs by leveraging local graph structure and automorphism equivariance. It addresses the limitations of current higher-order GNNs, which often struggle with computational complexity and scalability. The proposed Schur Nets offer a practical and efficient solution, potentially impacting various applications where GNNs are used, such as drug discovery and materials science. This work opens exciting new avenues for research into more expressive and efficient GNN architectures.
Visual Insights#

The figure shows the impact of varying the number of channels within the Schur layer on model performance. It reveals that increasing the number of channels initially improves performance, but that after a certain point (around 4-6 channels), there are diminishing returns and even a slight performance decrease, potentially due to overfitting or the limited number of distinct eigenvalues for the selected cycles (5 and 6). The experiment uses cycles of size 5 and 6, suggesting that model behavior may differ with other cycle lengths.

This table compares the performance of the Schur Layer and Linmaps methods with different message passing schemes on the ZINC-12K dataset. The message passing scheme determines when two subgraph representations communicate (i.e., overlap of 1 or more vertices, or overlap of 2 or more vertices). The results show that the Schur Layer consistently outperforms Linmaps across various message passing schemes, indicating its improved efficiency and accuracy.
In-depth insights#
Equivariant GNNs#
Equivariant Graph Neural Networks (GNNs) are a powerful class of models that leverage the inherent symmetries of graph data. Equivariance ensures that the network’s output transforms consistently with changes in the input representation, such as node re-ordering. This is crucial for tasks where the absolute ordering of nodes is meaningless, like molecular property prediction or social network analysis. Traditional GNNs often fall short in fully exploiting these symmetries, especially when dealing with complex local graph structures. Higher-order GNNs address this limitation by considering subgraphs and richer message passing schemes, but ensuring equivariance within these more complex architectures becomes increasingly challenging. The paper explores methods to achieve efficient, robust equivariance, particularly focusing on the automorphism group of subgraphs. Spectral graph theory provides a computationally tractable route to construct a basis for equivariant operations directly from the graph Laplacian, bypassing the need for explicit group representation theory. This approach, implemented as Schur layers, enhances GNNs expressive power, leading to improved empirical results on molecular property prediction benchmarks, offering a significant contribution to the field of equivariant GNNs.
Schur Layer Design#
The Schur layer design is a novel approach to constructing equivariant linear maps in higher-order graph neural networks. It leverages spectral graph theory to bypass the computationally expensive task of explicitly determining the automorphism group and its irreducible representations. Instead, it uses the graph Laplacian’s eigenspaces to define invariant subspaces, enabling the creation of linear maps that are inherently equivariant to the subgraph’s automorphism group. This simplification is a significant advantage over traditional group-theoretic methods. However, it’s crucial to note that this approach might not capture the full set of possible equivariant maps, possibly leading to a less expressive model compared to more computationally intensive group-theoretic methods. The effectiveness of the Schur layer depends heavily on the properties of the subgraph’s Laplacian, particularly the number of distinct eigenvalues and their multiplicities. Future work should focus on quantifying this potential gap in expressiveness and exploring strategies to enhance the expressivity of the Schur layers while maintaining computational efficiency.
Spectral Approach#
The spectral approach offers a computationally efficient alternative to traditional group-theoretic methods for constructing automorphism-equivariant operations in higher-order graph neural networks. By leveraging the graph Laplacian’s eigen-decomposition, it bypasses the need for explicitly determining the automorphism group and its irreducible representations. This simplification is crucial for scalability, especially when dealing with diverse and complex subgraphs. The approach constructs a basis for equivariant operations directly from the eigenspaces, ensuring invariance under automorphisms without computationally expensive group-theoretic computations. The resulting “Schur layers” efficiently incorporate subgraph structure into the network’s computations. While potentially less expressive than the full group-theoretic approach, the spectral method provides a practical compromise offering significant gains in efficiency and applicability to larger graphs and complex topologies. The theoretical underpinnings are rigorously established, providing confidence in the method’s correctness and equivariance properties. Empirical results demonstrate that this approach significantly enhances the performance of higher-order GNNs, highlighting the value of its computational efficiency and practical applicability.
Benchmark Results#
The benchmark results section of a research paper is crucial for evaluating the proposed method’s performance. A strong benchmark section will compare the new approach against a variety of existing state-of-the-art methods on multiple standard datasets. The metrics used for comparison should be clearly defined and relevant to the problem being addressed. A comprehensive comparison allows readers to gauge the strengths and weaknesses of the new approach relative to established techniques. The results should be presented clearly and concisely, often using tables and figures to visualize the performance differences. Statistical significance testing is also essential to ensure that observed improvements are not merely due to chance. Furthermore, a thoughtful discussion of the results is needed to highlight any unexpected findings, limitations, and areas for future work. A robust benchmark section is vital for establishing the credibility and impact of the research.
Future Directions#
Future research could explore several promising avenues. Improving the efficiency and scalability of Schur Nets is crucial, particularly for larger graphs where computational demands currently limit applicability. This could involve exploring more efficient algorithms for spectral decomposition or developing approximations that maintain accuracy while reducing computational complexity. Another critical area is extending the framework to handle different types of subgraphs and higher-order interactions. The current approach focuses primarily on cycles; broadening the range of recognizable structural motifs would significantly enhance the model’s expressivity. Finally, thorough theoretical analysis is needed to understand the limitations of the spectral approach and rigorously compare it to the group-theoretic framework. While empirical results are promising, a deeper theoretical understanding is needed to determine the precise conditions where Schur Nets outperform alternative approaches and to guide further development.
More visual insights#
More on tables
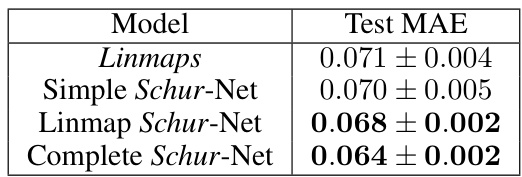
This table shows an ablation study on different ways of using the Schur layer in a neural network model. The results demonstrate that applying the Schur layer at different stages of processing subgraph information leads to varying improvements in predictive accuracy (measured by Test MAE). Specifically, using the Schur Layer in conjunction with the original cycle representation shows the largest performance gains.
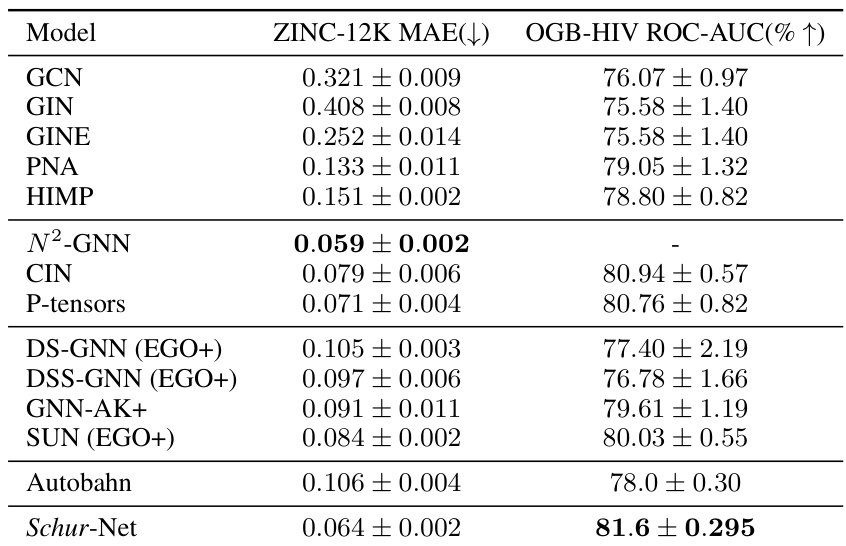
This table compares the performance of various graph neural network (GNN) models on two benchmark datasets: ZINC-12K (for predicting molecular properties) and OGB-HIV (for predicting the activity of HIV inhibitors). The table shows the mean absolute error (MAE) for ZINC-12K and the area under the receiver operating characteristic curve (ROC-AUC) for OGB-HIV. The models include classical GNNs (GCN, GIN, GINE, PNA, HIMP), higher-order GNNs (N2-GNN, CIN, P-tensors), subgraph-based GNNs (DS-GNN, DSS-GNN, GNN-AK+, SUN), and the Autobahn architecture. The results demonstrate that the proposed Schur-Net model outperforms many existing methods, particularly on the OGB-HIV dataset.
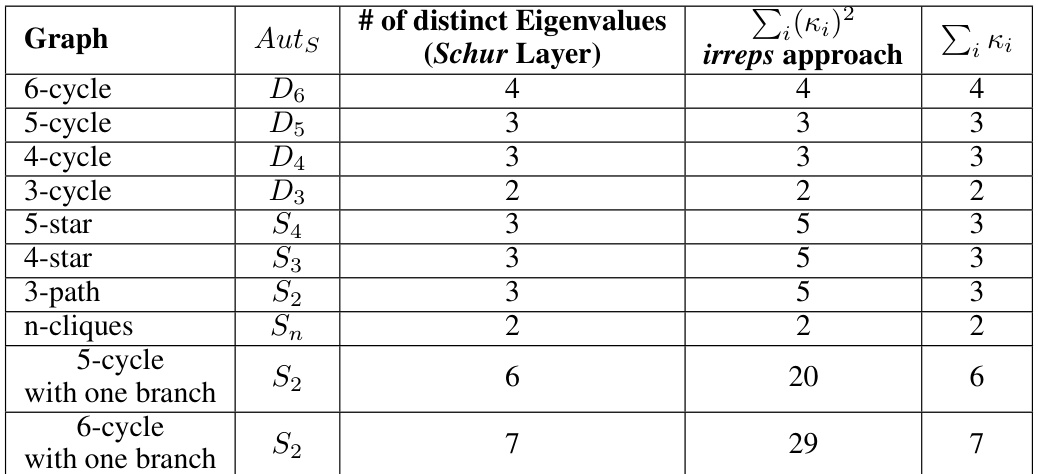
This table compares the number of equivariant maps obtained by the spectral approach (Schur layer) with the number obtained by the group theoretical approach for several small graphs. It demonstrates that the spectral method, which is computationally more efficient, achieves comparable results to the theoretically complete, yet computationally intensive group-theoretic approach. The table shows the automorphism group (Auts), the number of distinct eigenvalues (used in the Schur layer), and the number of irreps obtained via the group-theoretic method, comparing them to show the closeness of the approximation.

This table compares the number of equivariant maps obtained using two different approaches: the eigenvalue decomposition (EVD) approach and the group theoretical approach. It illustrates the potential gap between these approaches for different types of graphs, highlighting the number of distinct eigenvalues found by the EVD approach versus the number of irreps (irreducible representations) obtained from the group theoretical approach. The table includes calculations for various graphs, such as cycles and stars, and shows how the number of distinct eigenvalues and irreps may differ. The methods of calculating these values are also described.

This table compares the performance of three different methods on the ZINC-12K dataset. The methods are: Linmaps (baseline), Schur layer (in place of MLP), and Schur layer (as learning new feature). The validation MAE is used as the evaluation metric. The results show that Schur layer (as learning new feature) achieves the best performance, followed by Schur layer (in place of MLP), and then Linmaps.

This table shows the results of experiments on the ZINC-12K dataset comparing the performance of two models: a baseline Schur-Net using only 5 and 6 cycles and an augmented Schur-Net that also includes cycles with up to three branches. The results demonstrate the impact of incorporating more diverse subgraph structures on model performance, with the augmented model achieving a lower validation MAE.

This table presents a comparison of the performance of Linmaps and Schur Layer on various datasets from the TUDataset benchmark. The performance metric is binary classification accuracy, reported as the mean ± standard deviation. The results demonstrate that Schur Layer generally improves upon Linmaps across different datasets.

This table compares the runtime per epoch of Linmaps and Schur Layer on the ZINC-12k and NCI1 datasets. The hyperparameters used are specified in the caption. The results show that Schur Layer’s increased expressiveness does not come at a significant computational cost.

This table compares the performance of the Schur layer and Linmaps methods on the ZINC-12k dataset using different sets of cycle sizes for higher-order message passing. The test MAE (Mean Absolute Error) is reported for both methods, showing that the Schur layer consistently outperforms the baseline Linmaps method.
Full paper#



















