↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Multi-view representation learning (MVRL) aims to learn unified representations from diverse data sources. Deep Canonical Correlation Analysis (DCCA) is a prominent MVRL technique, but suffers from ‘model collapse’, where performance drastically drops during training. This makes it challenging to determine optimal stopping points, hindering widespread adoption. Existing solutions like early stopping prove insufficient.
This paper introduces NR-DCCA, a novel method incorporating noise regularization to combat model collapse. NR-DCCA leverages the ‘Correlation Invariant Property’ to ensure stable weight matrices, preventing the performance decline. The proposed method is shown to consistently outperform baselines on synthetic and real-world datasets, demonstrating its effectiveness and generalizability to other DCCA-based methods. The paper also provides a framework for generating synthetic datasets with varied common and complementary information, allowing for a comprehensive evaluation of MVRL techniques.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with multi-view representation learning (MVRL) and deep canonical correlation analysis (DCCA). It addresses the prevalent issue of model collapse in DCCA, offering a novel solution that improves model stability and performance. This work provides both theoretical justifications and empirical evidence, expanding the applicability and reliability of DCCA-based methods. The proposed noise regularization technique is also generalizable to other DCCA variants, significantly impacting the field and opening avenues for further research on robust and efficient MVRL methods.
Visual Insights#
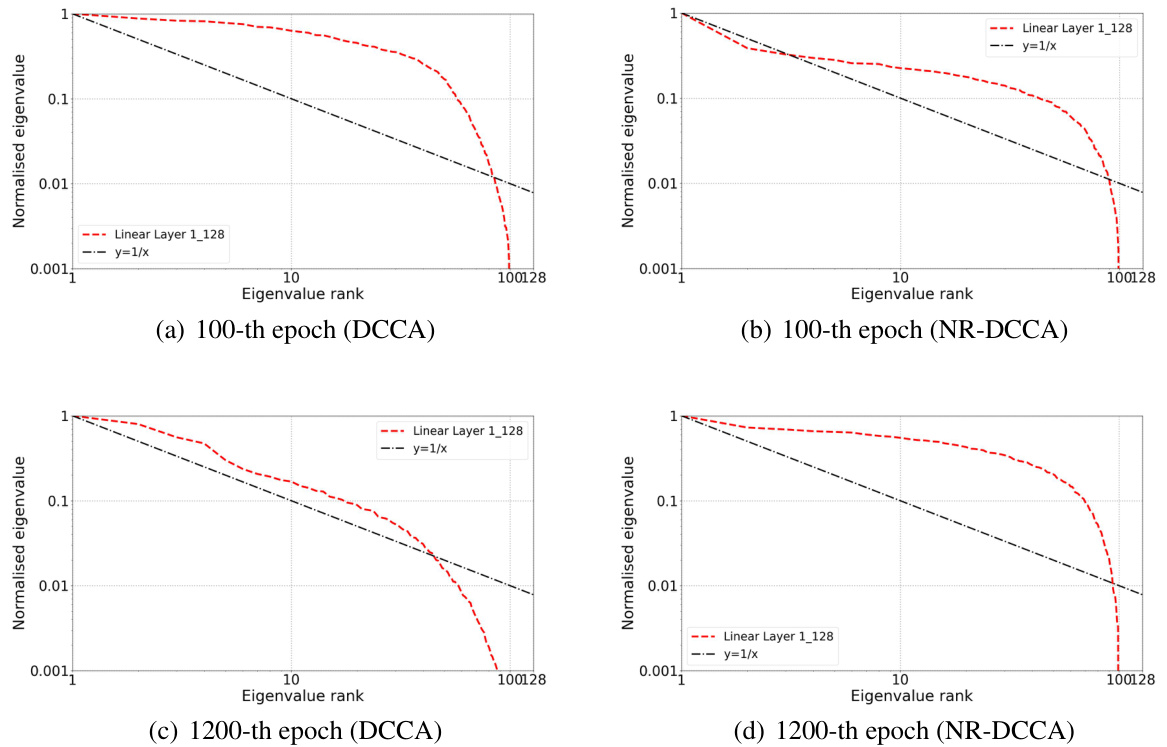
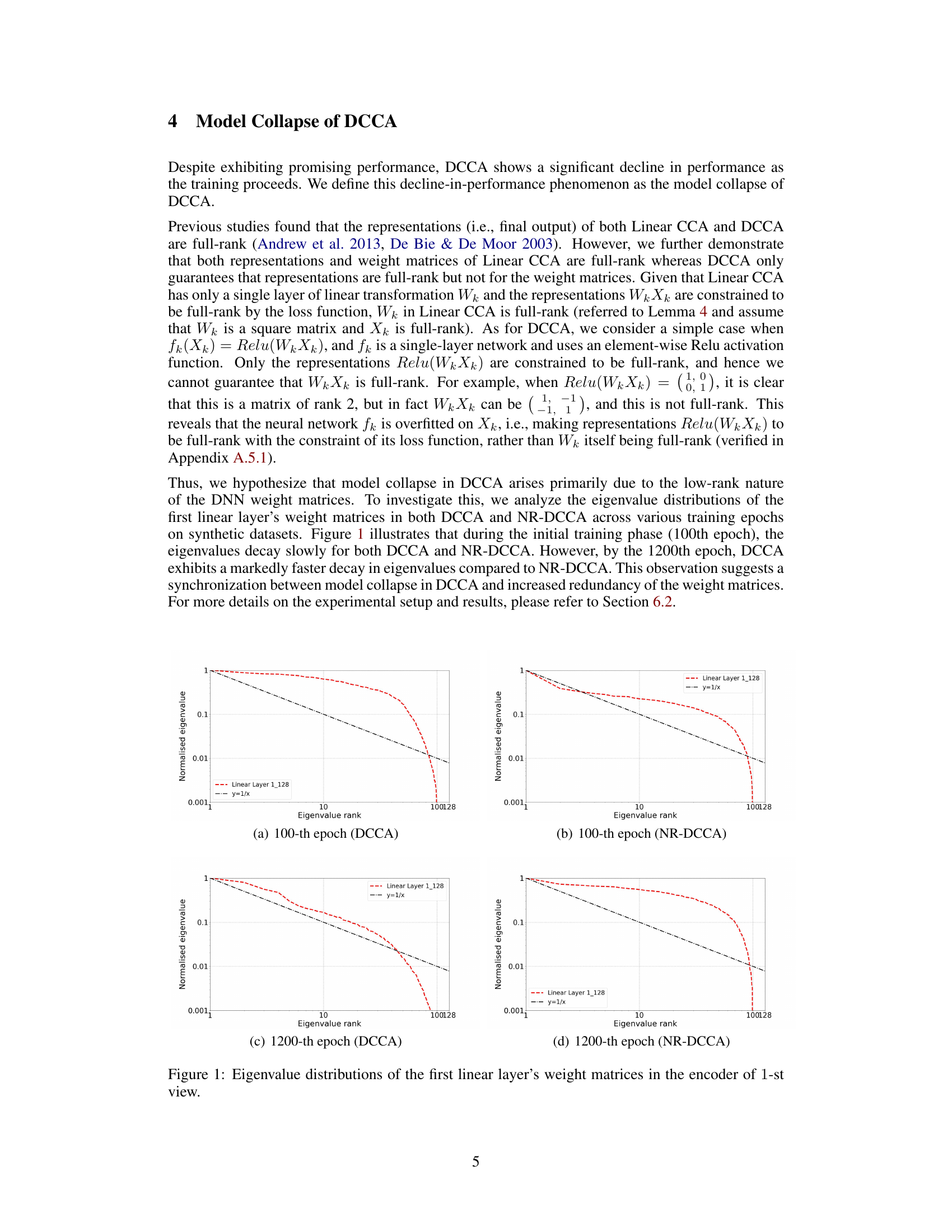
This figure shows the eigenvalue distributions of the first linear layer’s weight matrices in the encoder of the first view at the 100th and 1200th epochs for both DCCA and NR-DCCA. It visually demonstrates the hypothesis that model collapse in DCCA is due to the low-rank nature of the DNN weight matrices. The plots show that at the 100th epoch, the eigenvalues decay relatively slowly for both methods. However, by the 1200th epoch, DCCA exhibits a much faster decay in eigenvalues compared to NR-DCCA, indicating increased redundancy in the weight matrices of DCCA and suggesting a link between this redundancy and model collapse. The plots are normalized and also include the y=1/x curve as a reference.

This table shows the performance comparison of DCCA and NR-DCCA with Gaussian noise and uniform noise at different epochs (100, 800, 1200). The results demonstrate that the NR-DCCA approach effectively suppresses model collapse, as evident by significantly higher R2 performance values compared to standard DCCA, especially at later training stages (800 and 1200 epochs). The performance is consistent whether using Gaussian or uniform noise.
In-depth insights#
DCCA’s Collapse#
The phenomenon of “DCCA’s Collapse” reveals a critical limitation in Deep Canonical Correlation Analysis. Initial high performance degrades significantly as training progresses, hindering widespread adoption. This collapse isn’t due to the learned representations becoming low-rank (as they remain full-rank), but rather the underlying weight matrices within the deep neural network progressively becoming low-rank. This redundancy limits the network’s expressiveness and results in the observed performance decline. The key is the Correlation Invariant Property (CIP); Linear CCA inherently possesses CIP, ensuring stable full-rank weight matrices. DCCA, lacking this inherent constraint, succumbs to low-rank weight matrices and thus performance collapse. Addressing this requires methods like the Noise Regularization proposed in the paper, forcing the network to maintain CIP and consequently, stable high-performing full-rank weight matrices, even during extended training.
NR-DCCA Method#
The NR-DCCA method is a novel approach to address model collapse in deep canonical correlation analysis (DCCA) by incorporating noise regularization. The core idea is to introduce random noise to the input data and enforce the correlation between the original data and the noise to remain invariant after transformation by the DCCA network. This constraint, termed the Correlation Invariant Property (CIP), prevents the network from overfitting and discovering low-rank solutions that lead to model collapse. Theoretical analysis shows a strong link between CIP and full-rank weight matrices, crucial for stable performance. The method outperforms baseline DCCA approaches in various experiments, demonstrating its effectiveness across different datasets. By forcing the network to maintain CIP, NR-DCCA successfully mimics the behavior of Linear CCA, which does not suffer from model collapse, effectively improving the stability and performance of DCCA-based multi-view representation learning.
Synthetic Data#
The effective utilization of synthetic data in evaluating multi-view representation learning (MVRL) methods is a crucial aspect of the research. Synthetic datasets offer a controlled environment to systematically assess the performance of algorithms, isolating the impact of specific factors like the amount of common and complementary information between views. A well-designed synthetic data generation framework, such as the one proposed in the paper, allows for a comprehensive evaluation across a range of scenarios, revealing strengths and weaknesses of different MVRL approaches. The capability to control the correlation between views by adjusting parameters like the common rate is particularly valuable, providing insights into how algorithms respond to varying levels of shared information. Moreover, the use of synthetic data enables a direct comparison with theoretical analysis, which may reveal the underlying properties that facilitate or hinder the performance of algorithms. The absence of real-world complexities in synthetic datasets facilitates a cleaner examination of model characteristics, which can be leveraged to better understand and improve the performance of MVRL models in more complex real-world settings. However, it is important to note that while synthetic data offers a highly controlled experimental setup, there is always a risk of overfitting to the specific characteristics of this data and not generalizing well to real-world scenarios.
Theoretical Proof#
A theoretical proof section in a research paper serves to rigorously establish the validity of claims made within the paper. It provides a formal, mathematical demonstration of a key result, often using axioms, definitions, and logical deduction. A strong theoretical proof section builds credibility by moving beyond empirical evidence alone and establishing the underlying principles that govern the observed phenomena. Rigorous proofs are crucial, especially when dealing with complex systems or novel concepts, as they provide a clear understanding and eliminate ambiguities. However, a well-written theoretical proof should also be accessible; it should clearly define all terms and concepts, proceed in a logical and step-by-step manner, and avoid unnecessary complexities. The level of mathematical detail should be appropriate for the target audience of the paper. The inclusion of a proof demonstrates the depth of the research and distinguishes it from purely empirical studies. Moreover, a sound theoretical proof not only validates the paper’s findings but also potentially suggests avenues for future research by revealing the core mechanisms and properties under consideration.
Future of NR#
The “Future of NR” (noise regularization) in multi-view representation learning (MVRL) holds significant promise. Extending NR beyond DCCA to other MVRL methods is crucial, ensuring broader applicability and improved robustness across diverse methodologies. Theoretical exploration into the interplay between NR, model collapse, and the correlation invariant property (CIP) should be further investigated, providing a deeper understanding of NR’s mechanism. Addressing the computational cost is vital for practical applications, particularly with high-dimensional data. Finally, exploring the synergy between NR and other regularization techniques, such as weight decay or dropout, could potentially unlock even more powerful regularization strategies for enhanced stability and generalization in MVRL.
More visual insights#
More on figures
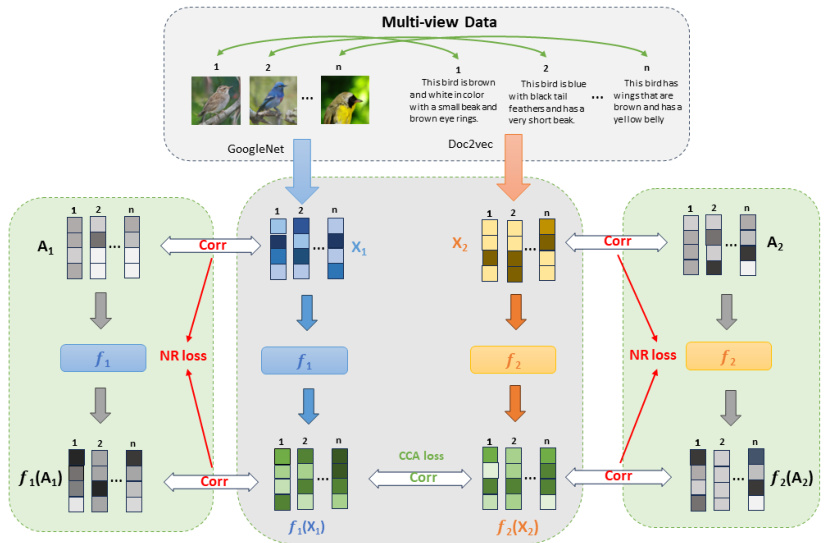
This figure illustrates the architecture of NR-DCCA, a novel method proposed in the paper to prevent model collapse in deep canonical correlation analysis (DCCA). The figure shows how the NR-DCCA model takes multi-view data as input, processes it using neural networks (fk), and incorporates a novel noise regularization (NR) loss to prevent model collapse. The NR loss is calculated by comparing the correlation between the original data and noise with the correlation between the transformed data and transformed noise. By minimizing this loss, the model is encouraged to maintain correlations that are robust to random noise. The diagram highlights the key components including multi-view data input, feature extraction using GoogleNet and Doc2Vec, correlation calculation, noise regularization and loss functions (CCA loss and NR loss), and the resulting unified representation. The CUB dataset is used as a specific example.
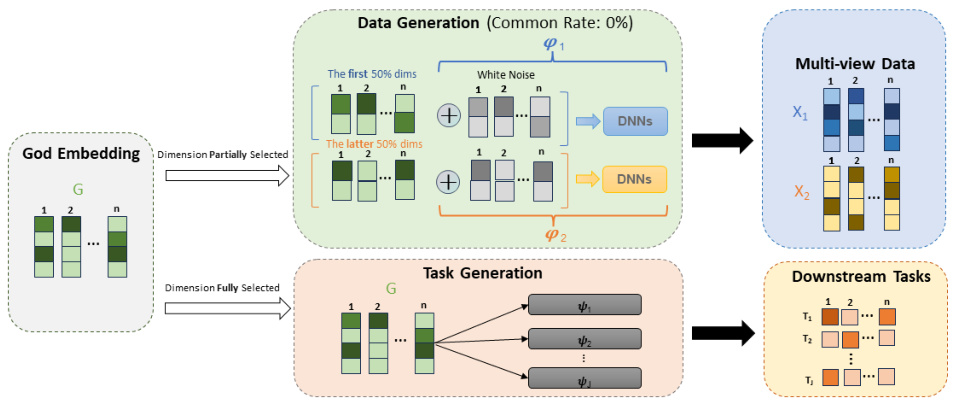
This figure illustrates the process of constructing synthetic datasets used to evaluate multi-view representation learning (MVRL) methods. It starts with a ‘God Embedding’ (G), a high-dimensional representation of the object. This embedding is then partially selected and transformed using non-linear functions (Φ1 and Φ2), and noise is added, to create the two views (X1 and X2) for the synthetic dataset. The common rate (shown here as 0%) determines the amount of shared information between the two views. Separately, downstream tasks (T1…Tj) are generated using a separate transformation (ψj) of the full God Embedding. This setup allows for controlled generation of datasets with varying levels of shared and complementary information between views.
The figure displays eigenvalue distributions of the first linear layer’s weight matrices of the encoder for the first view across different training epochs (100th and 1200th epochs) for both DCCA and NR-DCCA methods. The plots reveal how eigenvalues decay over time. In the 100th epoch, both DCCA and NR-DCCA show a gradual decay. However, by the 1200th epoch, DCCA displays a significantly faster decay compared to NR-DCCA, suggesting increased redundancy in DCCA’s weight matrices.

This figure shows the performance of different methods (LINEAR CCA, DCCA, DCCAE, DCCA_PRIVATE, and NR-DCCA) on three real-world datasets: PolyMnist, CUB, and Caltech101. Each dataset is tested with a varying number of views (indicated in parentheses in the dataset name). The graphs illustrate the F1 score over epochs, demonstrating the stability and performance of each method on the different datasets. NR-DCCA shows consistently high F1 scores across all datasets, indicating robustness and superior performance compared to the other methods.

The figure shows the effects of different ridge regularization parameters (r) on the performance of DCCA on the CUB dataset. Three different metrics are plotted against the ridge parameter values: 1. F1_performance: The F1 score, a measure of a model’s accuracy in a classification task. 2. Corr_in_features: Correlation between features within the data itself. 3. Corr_with_noise: Correlation between the features and random noise added to the data. The plot reveals how varying the ridge parameter impacts these three aspects of model performance. It illustrates the effect of ridge regularization on DCCA, demonstrating its impact on accuracy and the correlation of the data both internally and with noise.
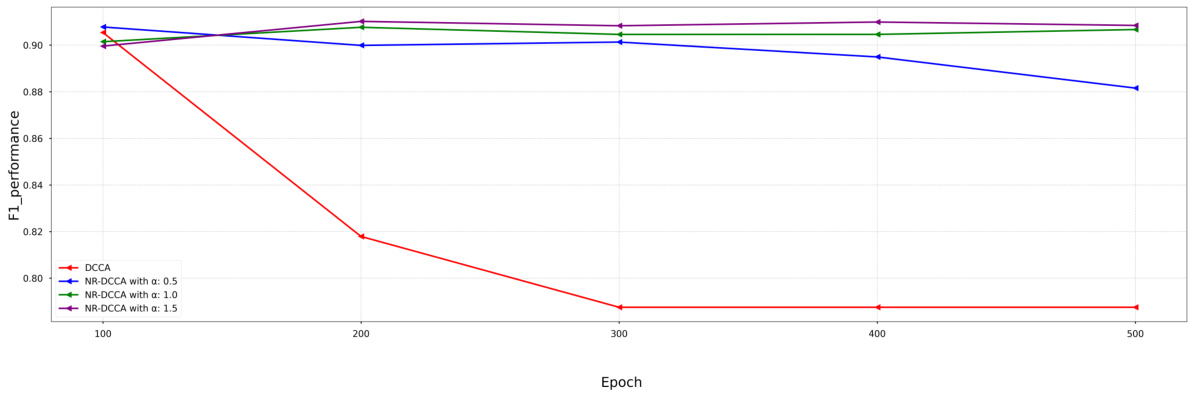
The figure shows the performance of NR-DCCA on the CUB dataset with different values of hyperparameter α. It demonstrates that using a too small value of α leads to model collapse while a too large value of α causes slow convergence. The optimal α is the smallest value that prevents model collapse, while maintaining high performance.
This figure shows the eigenvalue distributions of the first linear layer’s weight matrices in the encoder of the first view for both DCCA and NR-DCCA at the 100th and 1200th epochs. The plots illustrate how the eigenvalues decay over time, representing the redundancy in the weight matrices. At the 100th epoch, both DCCA and NR-DCCA show a relatively slow decay. However, by the 1200th epoch, the eigenvalues in DCCA decay much faster than in NR-DCCA, indicating increased redundancy and supporting the hypothesis that model collapse in DCCA is linked to low-rank weight matrices. The y=1/x line serves as a reference for comparison.

This figure visualizes the learned representations of different multi-view representation learning (MVRL) methods on the CUB dataset using t-SNE. Each point represents a data point, and the color indicates the class label. The visualization helps to understand how well each method separates the data points into distinct clusters according to their class labels and the level of dispersion within each cluster. Ideally, points of the same class should cluster together tightly but not overlap significantly with other clusters, demonstrating the preservation of distinctive features of the data and the ability to learn a meaningful representation of the data.
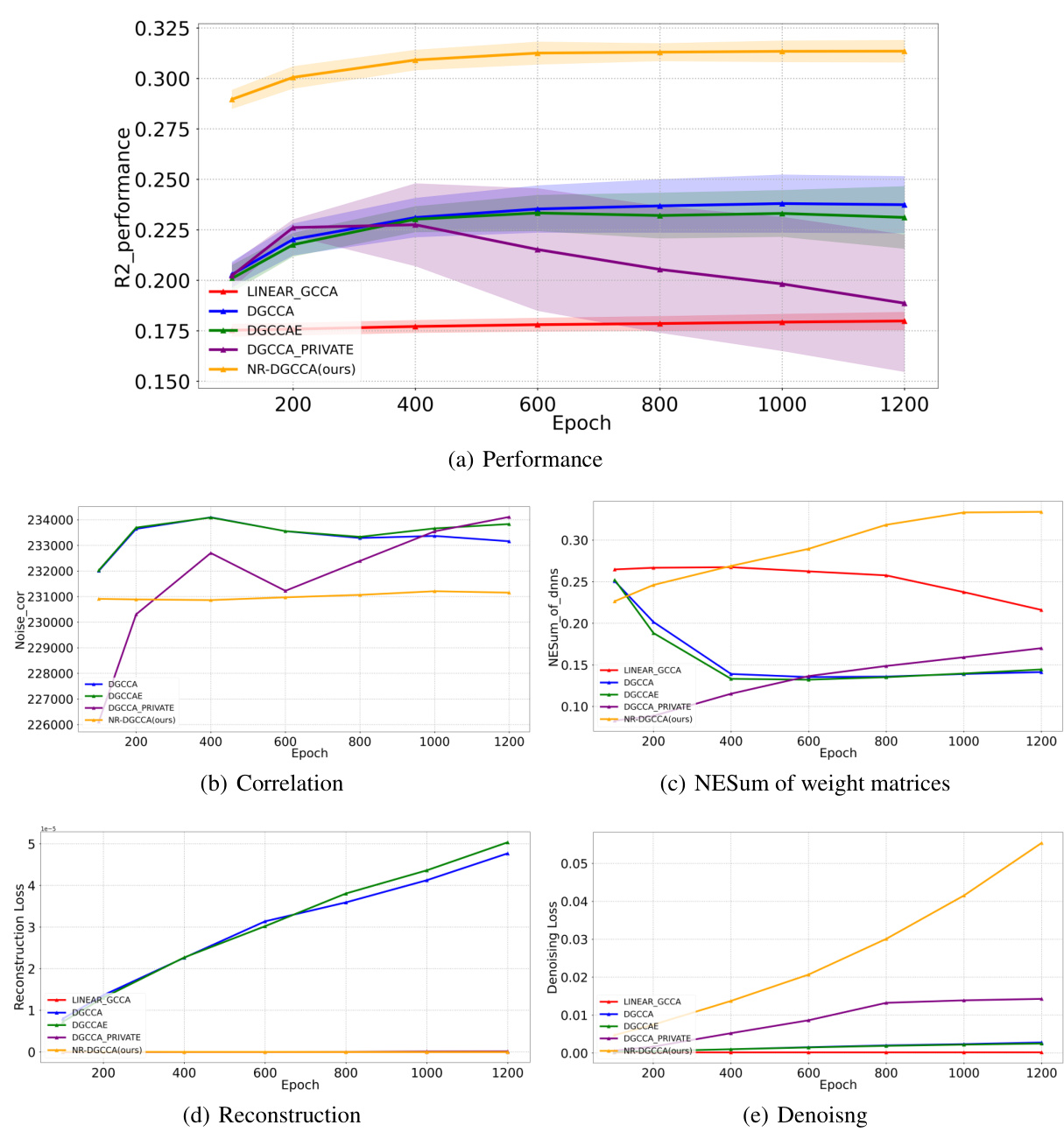
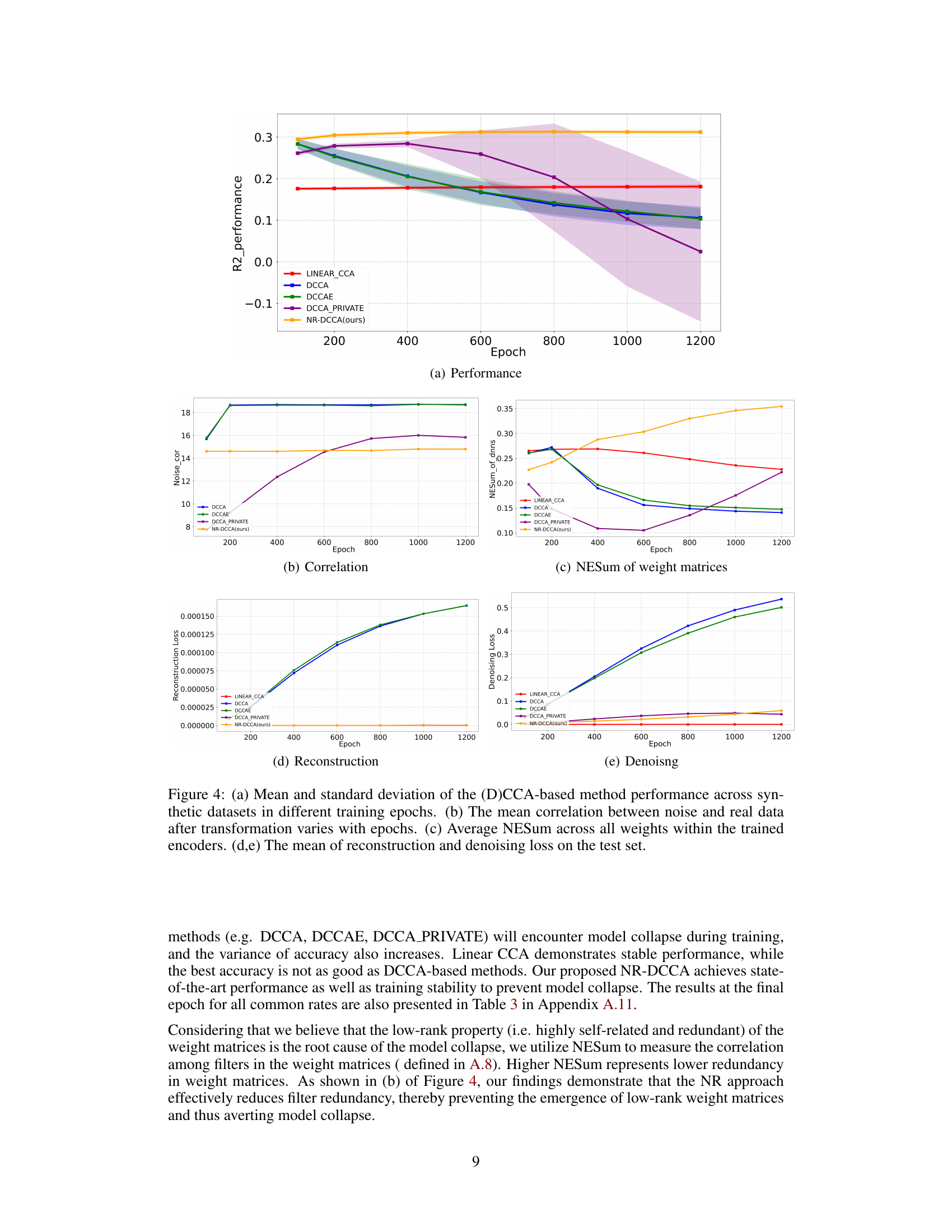
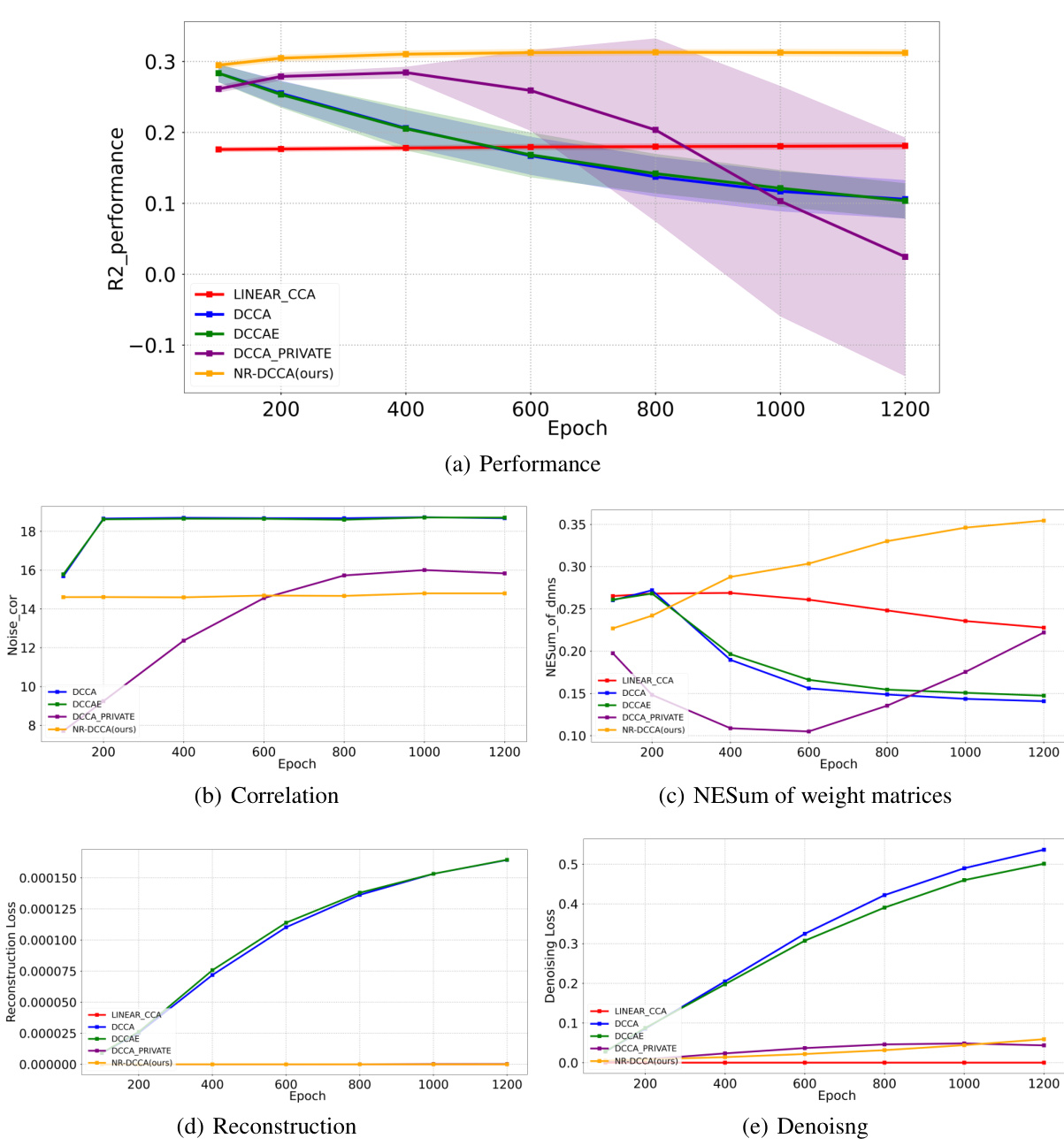
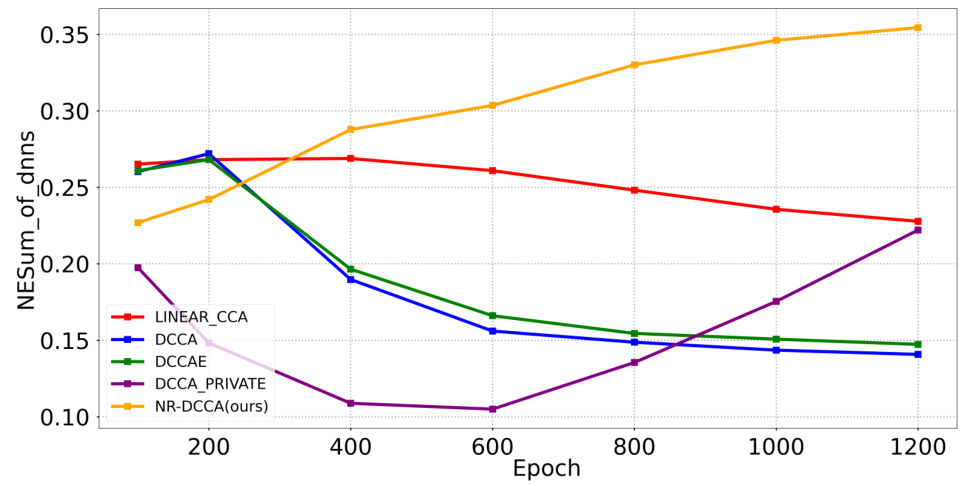
This figure visualizes the performance of different methods across various training epochs on synthetic datasets. Subfigure (a) shows the mean and standard deviation of R2 performance for each method across different epochs. Subfigure (b) displays the correlation between noise and real data after transformation. Subfigure (c) presents the average NESum (Normalized Eigenvalue Sum) across all weights in the trained encoders. Subfigures (d) and (e) show the mean reconstruction and denoising loss on the test set, respectively, as a function of the training epoch. The results demonstrate the stability and performance of NR-DCCA compared to other methods in preventing model collapse.

The figure shows the performance of various DGCCA methods on three real-world datasets: PolyMnist, CUB, and Caltech101. For PolyMnist, the number of views varies from 2 to 5. The x-axis represents the training epoch, while the y-axis represents the F1 score. The figure helps to visualize the stability and performance of different methods across various datasets and view numbers. The lines for each method demonstrate performance trends over time.
More on tables

This table presents the performance comparison of DCCA and NR-DCCA models trained with different numbers of hidden layers (1, 2, and 3). The results (R2 values) are reported for three different epochs (100, 800, and 1200) to illustrate the performance change during training. It shows how the model performance of DCCA declines with increasing depth, demonstrating model collapse, while the NR-DCCA method maintains relatively stable performance.
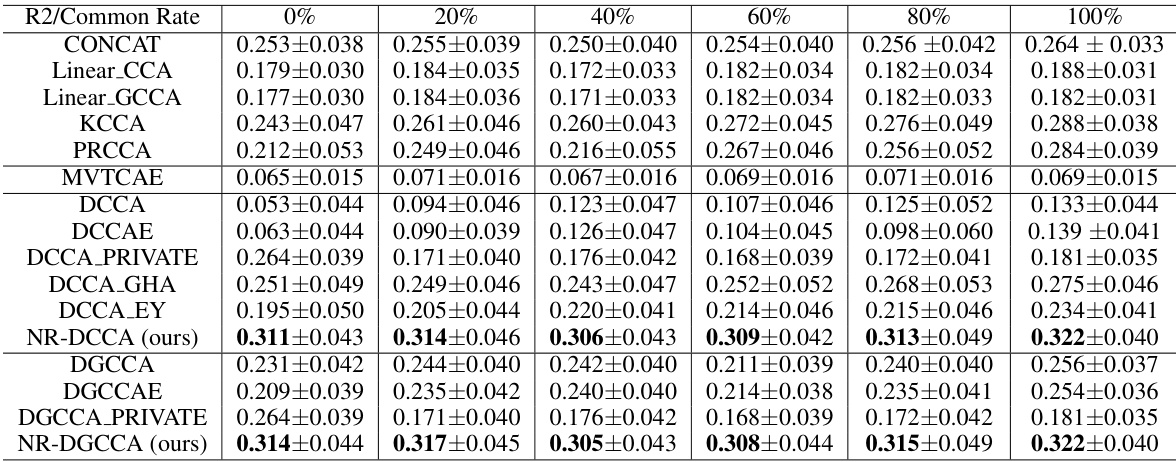
This table presents the performance of various multi-view representation learning (MVRL) methods across synthetic datasets with varying common rates (0%, 20%, 40%, 60%, 80%, 100%). The results represent the mean and standard deviation of the R2 score across 50 downstream regression tasks. The table allows for comparison of different MVRL approaches in controlled settings.
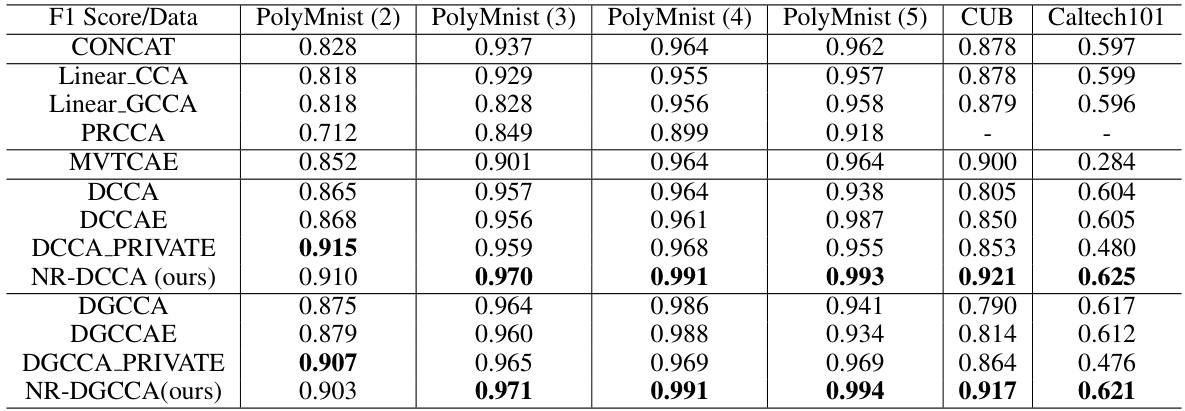
This table presents the performance of various multi-view representation learning (MVRL) methods on three real-world datasets: PolyMnist, CUB, and Caltech101. For each dataset, the F1 score (for classification tasks) is reported for different methods. The number of views used for each dataset is indicated in parentheses. The table allows for a comparison of the performance of different methods across various datasets and different numbers of views, highlighting the effectiveness and robustness of the proposed NR-DCCA method.

This table compares the computational complexity of different DCCA-based methods. The complexity is analyzed based on the number of views (K), number of samples (N), feature dimensions (D), number of hidden layers (L), number of neurons per layer (H), and the dimensionality of the unified representation (M). The table breaks down the complexity for each step involved in the different methods, such as noise generation, encoding and decoding using MLPs, reconstruction loss calculation, correlation maximization, and noise regularization. The complexities are expressed in Big O notation.
Full paper#