↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current SDF-based methods for 3D surface reconstruction often struggle with capturing fine details and intricate structures, leading to visible defects. This is attributed to two main factors: limitations in SDF-to-density representation and issues with geometric regularization. These issues hinder the optimization of the SDF field, resulting in suboptimal surface quality.
NeuRodin tackles these challenges with a two-stage approach. The first stage uses a coarse optimization process similar to density-based methods to handle topological changes effectively, while the second stage refines the reconstruction to produce smooth surfaces. This innovative framework incorporates local adaptive parameters for SDF-to-density conversion and a novel loss function to improve the alignment between volume rendering and implicit surface representations. Extensive evaluations demonstrate its superiority, particularly for scenes with intricate details.
Key Takeaways#
Why does it matter?#
This paper is important because it presents NeuRodin, a novel two-stage framework that significantly improves the accuracy and detail of neural surface reconstruction, addressing limitations of existing SDF-based methods. Its innovative strategies for handling topology and reducing artifacts, along with the establishment of a new benchmark for ScanNet++, make it a valuable contribution to the field. The findings offer new avenues for research in high-fidelity 3D reconstruction and will likely influence future work.
Visual Insights#

This figure showcases the NeuRodin framework’s ability to reconstruct complex 3D scenes from RGB images with high fidelity. It highlights the method’s capacity to recover both large-scale structures and fine-grained details, demonstrating its effectiveness in handling intricate geometries.

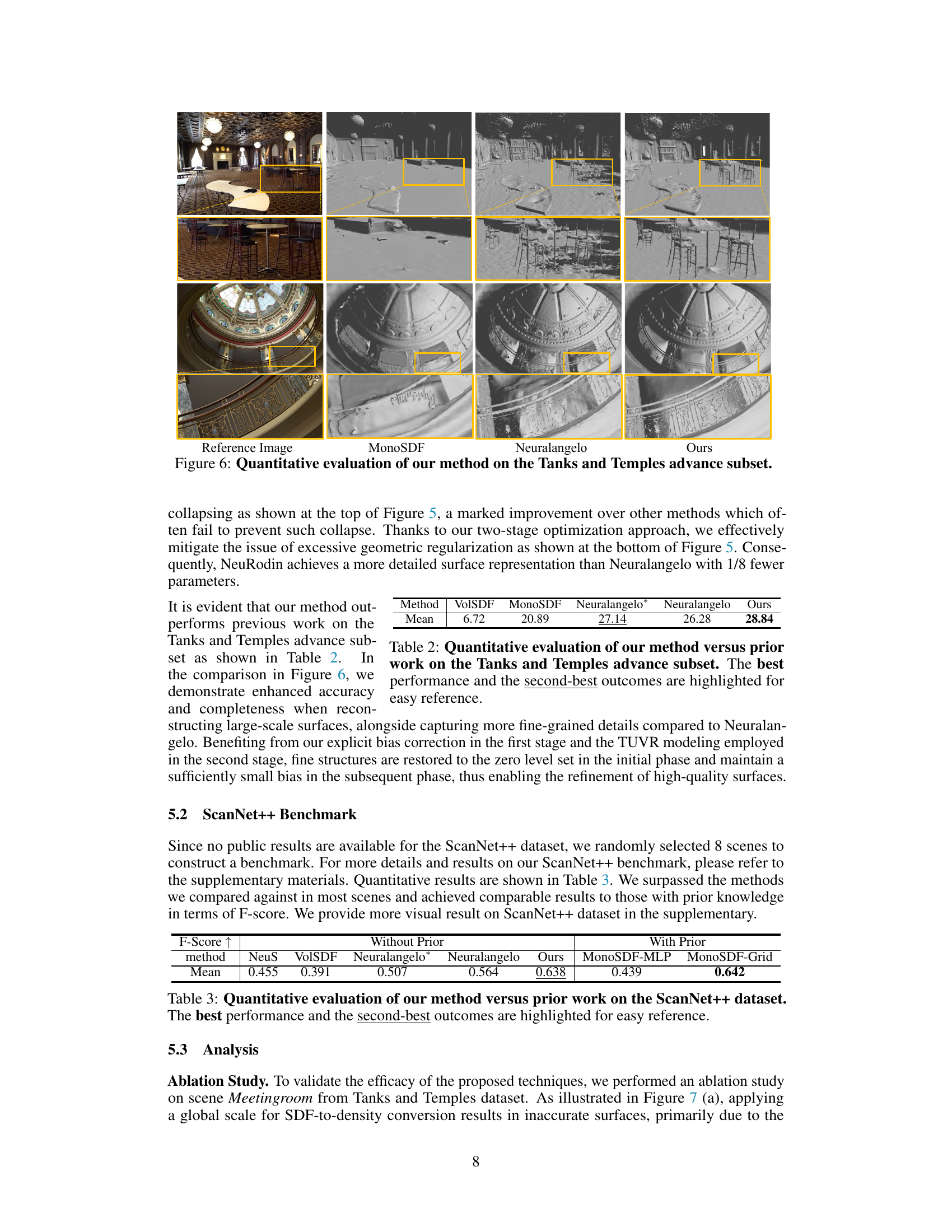
This table presents a quantitative comparison of the proposed NeuRodin method against several state-of-the-art techniques on the Tanks and Temples dataset’s training subset. The evaluation metric is F-Score, a measure of surface reconstruction accuracy. The table highlights the best and second-best performing methods for each scene, showcasing NeuRodin’s superior performance. It also notes that NeuRodin uses the same hash grid parameters as Neuralangelo for fair comparison.
In-depth insights#
SDF-Density Issues#
The core challenge lies in effectively bridging the gap between the Signed Distance Function (SDF) representation and the density field used for volume rendering. SDF-based methods often struggle to maintain high-fidelity surface reconstruction because of inherent limitations in representing arbitrary density values. Directly converting SDF values to density often leads to uniform density across level sets, masking intricate geometric detail. This is exacerbated by geometric regularization, which, while aiming to smooth the surface, can stifle the accurate capture of fine details and complex topologies. The uniform density assignment from SDF-to-density conversion is a critical issue, introducing biases and inaccuracies. Furthermore, the misalignment between the implicit surface and the geometric representation within the volume rendering framework often leads to smooth surfaces positioned incorrectly. Addressing these issues demands innovative methods for robust and accurate SDF-to-density mapping and the development of optimization strategies that prioritize fidelity while mitigating over-regularization.
NeuRodin’s Stages#
NeuRodin employs a two-stage optimization strategy to achieve high-fidelity surface reconstruction. The initial stage focuses on coarse reconstruction, prioritizing accurate surface topology and minimizing the influence of geometric regularization. This is accomplished by treating the SDF field similarly to a density field, promoting flexibility in handling complex topologies. A crucial innovation is the introduction of stochastic-step numerical gradient estimation, which injects uncertainty into the geometric regularization process, preventing over-smoothing of fine details. The second stage refines the coarse reconstruction, enhancing smoothness through standard geometric regularization. This two-stage approach effectively addresses the limitations of prior SDF-based methods that often struggle to balance geometric detail with accurate surface representation. The explicit bias correction mechanism, implemented in both stages, ensures the alignment between the implicit surface’s zero-level set and the geometric representation within the rendering framework, further boosting accuracy. This stage-wise procedure allows for effective optimization of intricate geometries while maintaining fidelity.
Bias Correction#
The concept of bias correction is crucial in the context of implicit neural surface reconstruction, as biases in the SDF-to-density conversion can lead to inaccurate surface representations. NeuRodin addresses this by introducing a novel loss function that explicitly aligns the maximum probability distance with the zero level set of the SDF. This method is particularly important during the initial, coarse optimization stage where topological changes are more frequent. Instead of relying on a global scaling factor, NeuRodin employs a local adaptive parameter for SDF-to-density conversion, further enhancing flexibility and accuracy. This strategy allows for a more nuanced handling of densities, preventing the uniform density assignments that hinder detailed geometric representation. The incorporation of a stochastic-step numerical gradient estimation, further aids in the bias correction and prevents over-regularization by introducing uncertainty into the optimization. This method maintains the natural zero level set for large-scale structures while allowing for complex geometries to be reconstructed accurately. Ultimately, NeuRodin’s multi-faceted approach towards bias correction showcases a significant improvement in high-fidelity surface reconstruction by reducing artifacts and improving the alignment of implicit and rendered geometric representations.
Benchmark Results#
The Benchmark Results section of a research paper is crucial for validating the proposed method’s performance. A strong benchmark rigorously compares the novel approach against existing state-of-the-art techniques on established datasets. Key metrics such as precision, recall, F1-score, and Intersection over Union should be reported, alongside a thorough analysis of these results. Statistical significance must be established, showing that observed improvements are not due to random chance. Qualitative evaluations, which include visualizations and detailed analyses of the results across diverse scenarios, enhance the credibility of the benchmarks. Furthermore, a robust benchmark considers the impact of various hyperparameters on model performance, and explores limitations and potential biases. Transparency is key; the choice of datasets and metrics must be clearly justified, alongside a discussion of the limitations of the benchmarking process itself. A comprehensive presentation of benchmark results builds strong confidence in the validity and generalizability of the research findings.
Future of NeuRodin#
The future of NeuRodin looks promising, building upon its strong foundation in high-fidelity neural surface reconstruction. Further research could explore advancements in handling dynamic scenes, moving beyond static RGB inputs to incorporate video data and temporal consistency. Improving the efficiency of the two-stage optimization process is crucial, particularly for large-scale scenes. This might involve exploring novel optimization algorithms or architectural changes. Addressing the limitations in textureless or ambiguous regions represents another key area for improvement. This could entail incorporating additional data sources or refining the density-based and SDF conversion methods. Finally, integrating NeuRodin with other computer vision tasks such as semantic segmentation or object recognition would enhance its practical utility. Such integration could lead to more comprehensive scene understanding and broader applications in augmented reality, robotics, and digital content creation. Ultimately, the future of NeuRodin hinges on addressing these challenges and expanding its capabilities to handle more complex and realistic environments.
More visual insights#
More on figures

This figure compares the results of three different methods for 3D surface reconstruction: Neuralangelo, Instant-NGP, and the authors’ proposed method, NeuRodin. It highlights the strengths and weaknesses of each approach. Neuralangelo struggles with complex topologies, resulting in inaccurate surfaces. Instant-NGP produces a noisy surface despite correctly positioning the overall structure. In contrast, the NeuRodin method accurately reconstructs a clean surface with fine details.
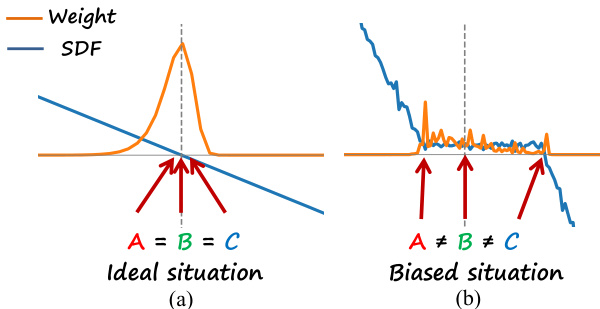
This figure illustrates the concept of density bias in SDF-based volume rendering. The ideal scenario (a) shows perfect alignment between the geometric representation from volume rendering (maximum probability distance and rendered distance) and the implicit surface (zero level set). The biased scenario (b) shows a misalignment, highlighting the challenge of aligning the geometric representation within the rendering framework with the implicit surface, leading to inaccuracies. This misalignment is a key problem addressed by the NeuRodin method.

This figure shows a heatmap visualizing the variance of estimated normals using a stochastic step size for gradient calculation. The variance is higher in areas with fine details and lower in large-scale areas. This property introduces uncertainty into the geometric regularization, allowing for flexibility in reconstructing fine details while maintaining stability for large-scale structures.

This figure compares three different methods for 3D surface reconstruction: Neuralangelo, Instant-NGP, and the authors’ proposed method. Neuralangelo struggles with complex shapes and produces incorrect surfaces. Instant-NGP correctly positions the surface but the result is noisy. The authors’ method achieves high-fidelity reconstruction, capturing fine details accurately.

The figure shows a qualitative comparison of the 3D surface reconstruction results on the training subset of Tanks and Temples dataset, comparing the results of NeuS, Neuralangelo, and the proposed method (Ours) with the ground truth point cloud. The comparison highlights the ability of the proposed method to accurately reconstruct intricate geometric details while maintaining the integrity of large-scale structures.

This figure demonstrates the ablation study performed on the proposed NeuRodin model. Each subfigure shows the results obtained by removing one of the key components of the model, highlighting the individual contribution of each component to the overall performance. The components are local scale for SDF-to-density conversion, stochastic-step numerical gradient estimation, explicit bias correction, and two-stage refinement. The full model combines all these components, showcasing superior reconstruction capabilities compared to the individual ablated models.

This figure compares the depth maps generated at iteration 7500 of the first stage by three different methods: Model A uses analytical gradient; Model B uses progressive numerical gradient estimation from Neuralangelo; Model C uses the authors’ proposed stochastic-step numerical gradient estimation. The results show that the authors’ method (Model C) produces a depth map that is more similar to Instant-NGP, but with a smoother and more natural zero level set, while Models A and B struggle to accurately capture the scene geometry. The final meshes produced by each method are also displayed, highlighting the improved accuracy and quality of the mesh produced using Model C.

This figure compares the depth maps generated by three different SDF-based volume rendering methods (VolSDF, NeuS, and TUVR) with and without the explicit bias correction proposed in the paper. The comparison highlights the impact of the bias correction on aligning the geometric representation within the rendering framework with that of the implicit surface. The results show that the explicit bias correction effectively reduces the bias, leading to more accurate depth maps.
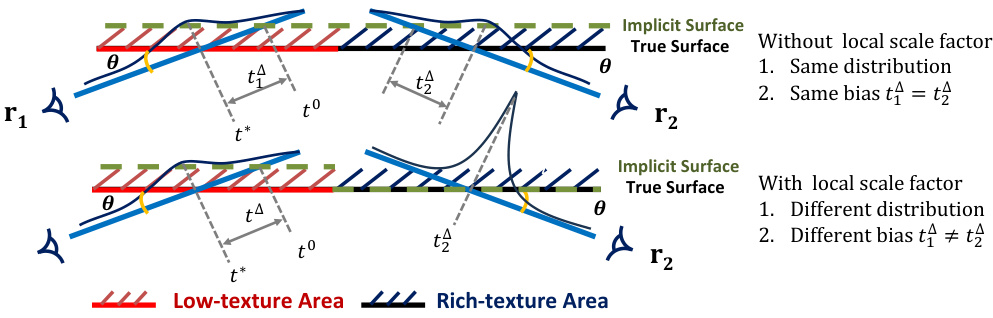
This figure illustrates the impact of using a global versus a local scale factor in SDF-to-density conversion. The left side shows a scenario without a local scale factor. In this case, both low-texture and rich-texture regions share the same distribution and bias, resulting in poor surface convergence, especially in the rich-texture region. The right side demonstrates the use of a local scale factor. Here, each region exhibits a unique distribution and bias, which allows for accurate localization and improved reconstruction quality, especially in areas with intricate details.

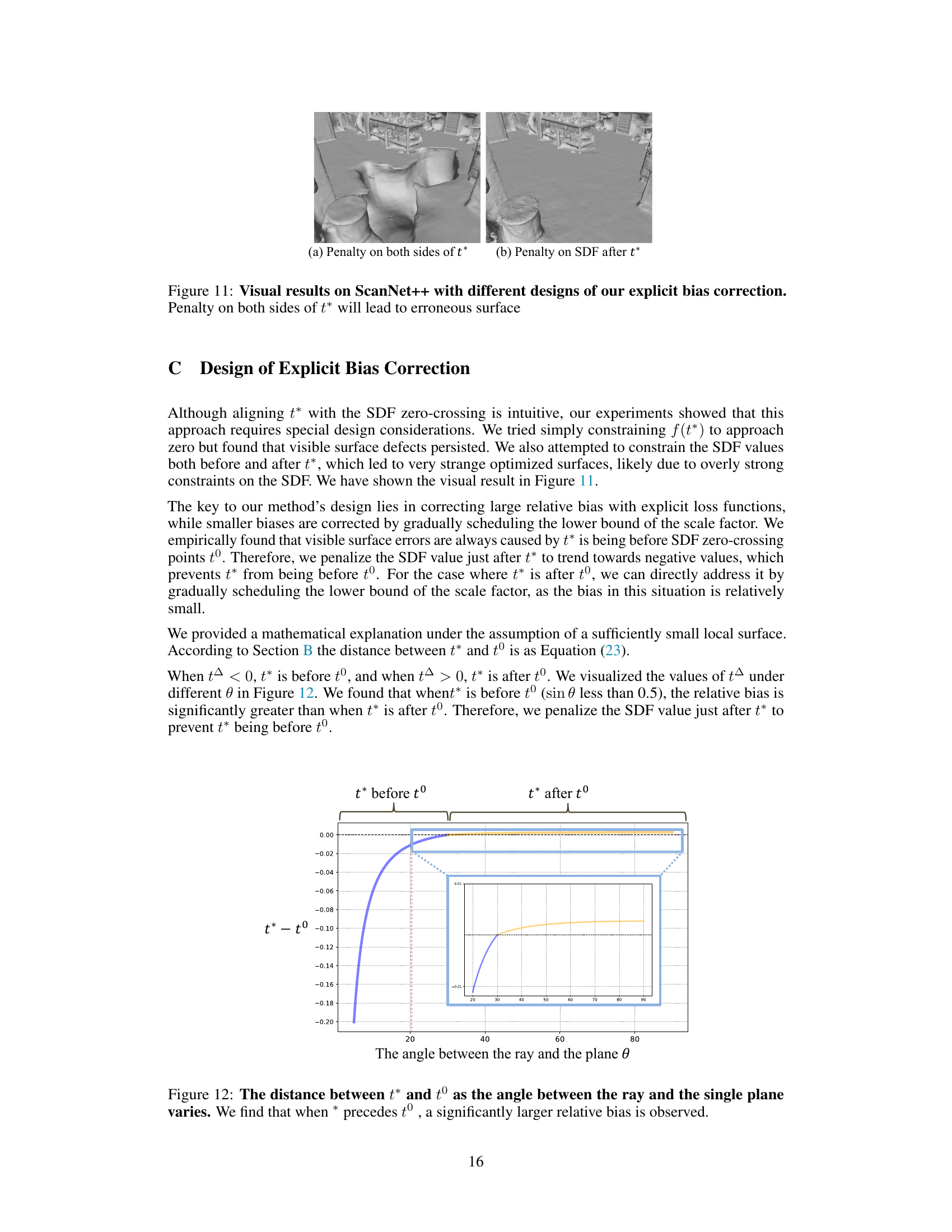
This figure shows a comparison of 3D surface reconstruction results on the ScanNet++ dataset using two different designs for the explicit bias correction method. The explicit bias correction aims to align the maximum probability distance with the zero level set in volume rendering. The left image (a) shows the results when a penalty is applied on both sides of t* (the maximum probability distance), which leads to an erroneous surface with artifacts. The right image (b) displays the results when the penalty is applied only on the SDF after t*, resulting in a significantly improved surface reconstruction with fewer artifacts.

This figure shows the visual results of applying different explicit bias correction methods on ScanNet++. The top row shows the reference images. The bottom row shows results from three different bias correction methods. The results show that applying penalty only to the SDF values after the maximum probability distance (t*) produces more accurate surfaces compared to methods that apply penalty on both sides of t*. This highlights the effectiveness of the proposed explicit bias correction method.
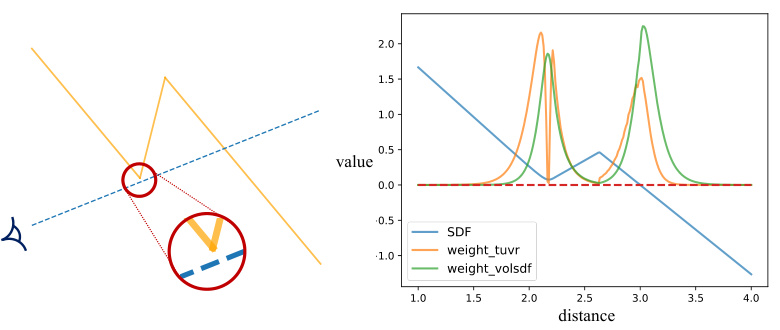
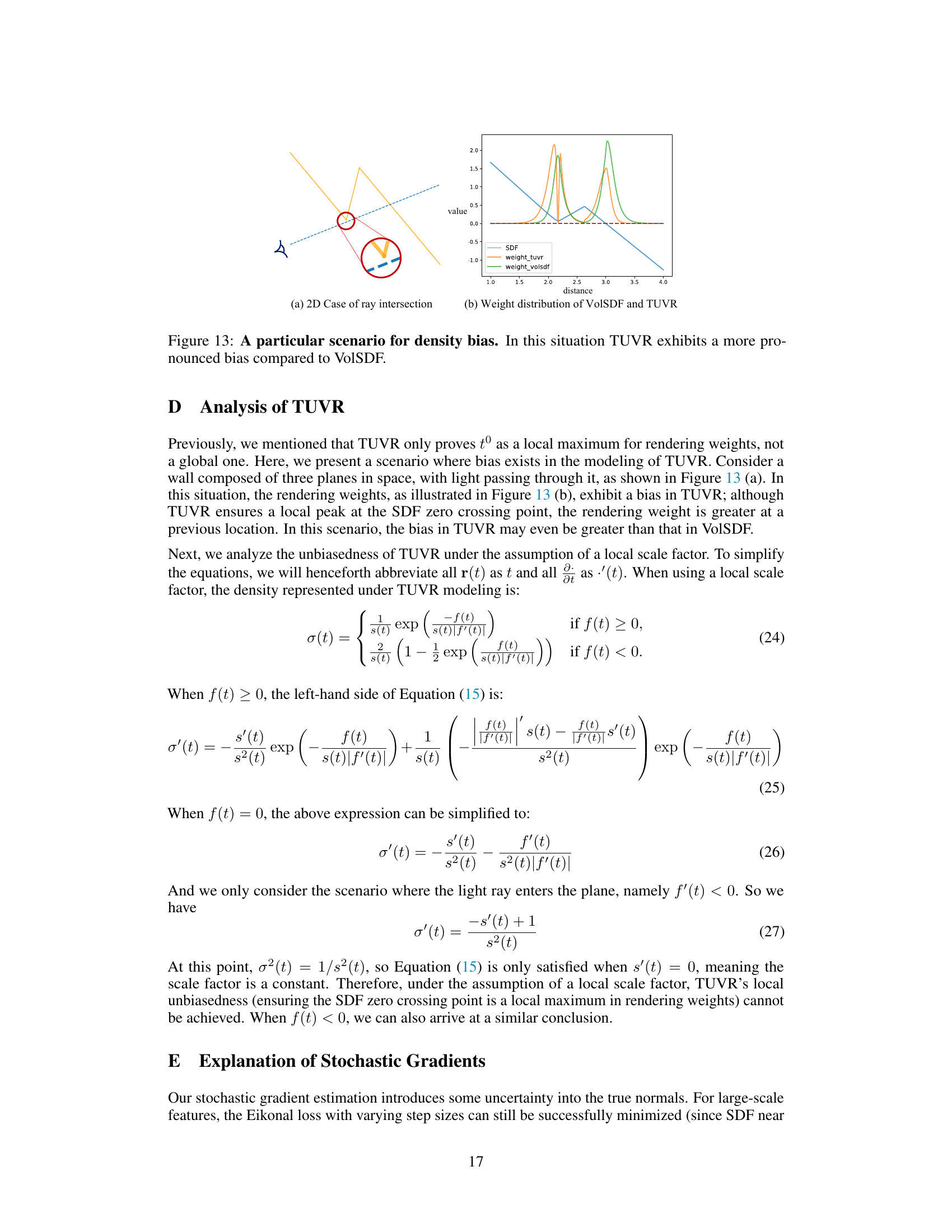
The figure illustrates a scenario where the TUVR method demonstrates a greater density bias compared to VolSDF. Panel (a) shows a 2D representation of a ray intersecting three planes. Panel (b) displays the rendering weight distribution for both TUVR and VolSDF along the ray. The key observation is that TUVR’s rendering weight has a larger peak at a location prior to the SDF zero-crossing point, indicating a greater bias than VolSDF.

This figure shows visual results on the ScanNet++ dataset comparing three different designs of the explicit bias correction method. The first design penalizes both sides of t*, resulting in an erroneous surface. The second design penalizes the SDF only after t*, which effectively addresses the bias issue. The third design employs the proposed method, resulting in an improved reconstruction of the surface.

This figure compares the results of three different methods for 3D surface reconstruction: Neuralangelo, Instant-NGP, and the authors’ proposed method, NeuRodin. It highlights the challenges faced by SDF-based methods (Neuralangelo) in handling complex topologies, and the limitations of density-based methods (Instant-NGP) in producing clean, detailed surfaces. NeuRodin, on the other hand, is shown to successfully reconstruct high-quality surfaces with fine details.

This figure shows the overall framework of NeuRodin, a two-stage method for high-fidelity neural surface reconstruction. The framework takes only posed RGB images as input and is able to reconstruct both large-scale areas and fine-grained details, even with intricate structures.

This figure shows the NeuRodin architecture, a two-stage framework for high-fidelity neural surface reconstruction. The framework is designed to handle intricate structures and uses only posed RGB images as input. The results demonstrate the ability to reconstruct both large-scale areas and fine-grained details.
More on tables

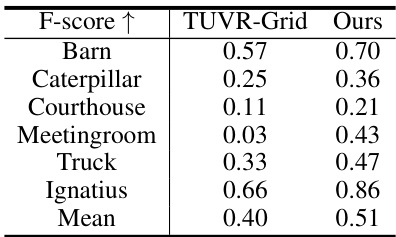
This table presents a quantitative comparison of the NeuRodin method against several state-of-the-art techniques on the Tanks and Temples advance subset. The metrics used for evaluation are not explicitly stated in the caption, but are likely related to 3D surface reconstruction accuracy. The results show NeuRodin outperforming other methods, highlighting its superior performance in reconstructing complex scenes.

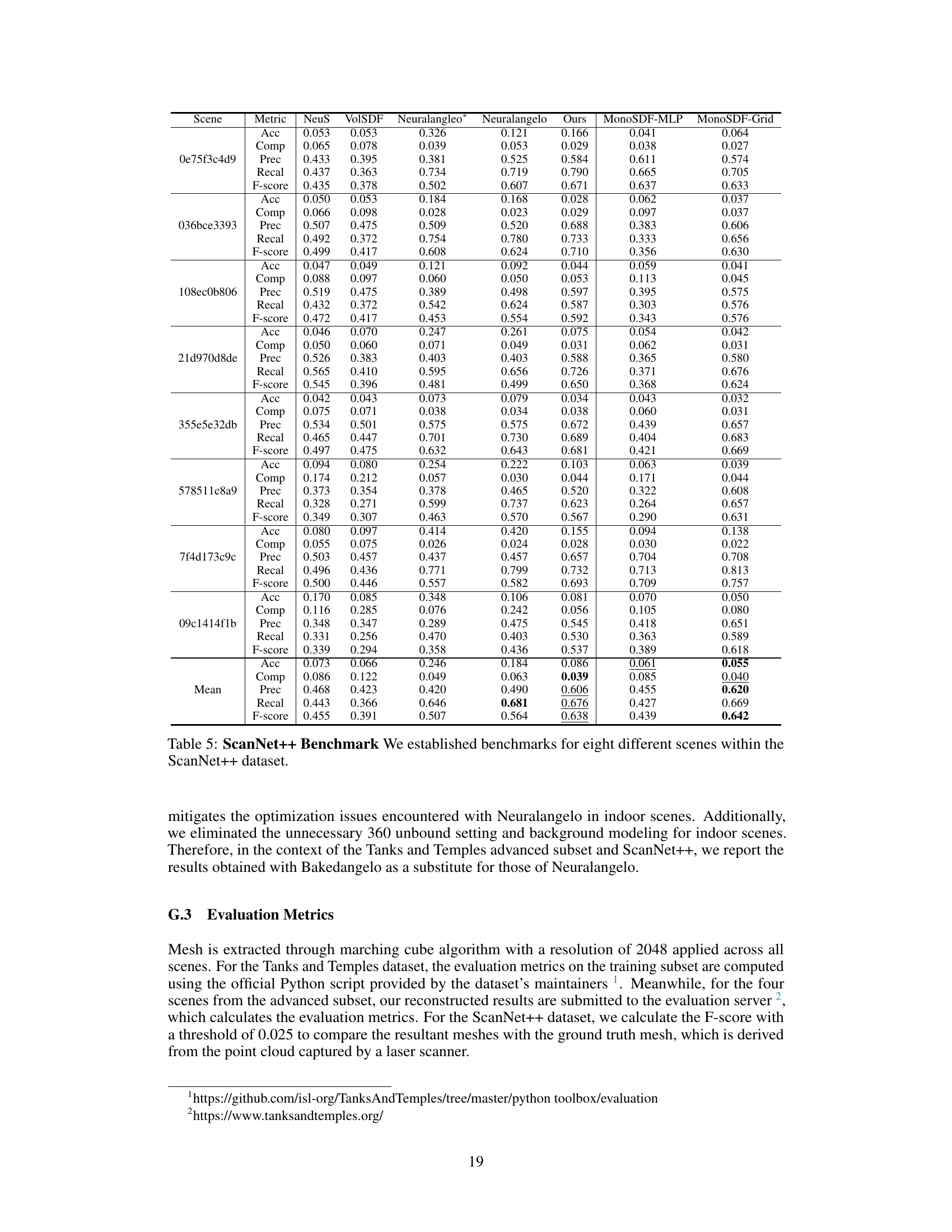
This table presents a quantitative comparison of the proposed NeuRodin method against several state-of-the-art techniques for 3D surface reconstruction on the ScanNet++ dataset. The comparison focuses on the F-Score metric, a common measure of surface reconstruction accuracy. The table is divided into two sections: ‘Without Prior’ and ‘With Prior.’ The ‘Without Prior’ section compares NeuRodin against methods that don’t leverage prior geometric information, while the ‘With Prior’ section contrasts NeuRodin with methods employing such information. The results highlight NeuRodin’s superior performance in both scenarios.

This table presents a quantitative comparison of the proposed NeuRodin method against several state-of-the-art techniques on the Tanks and Temples training dataset subset. The evaluation metric is the F-score, a measure of surface reconstruction accuracy. The table highlights the best and second-best performing methods for each scene, demonstrating NeuRodin’s superior performance compared to the baselines. It is important to note that NeuRodin uses the same hash grid parameters as Neuralangelo for fair comparison.
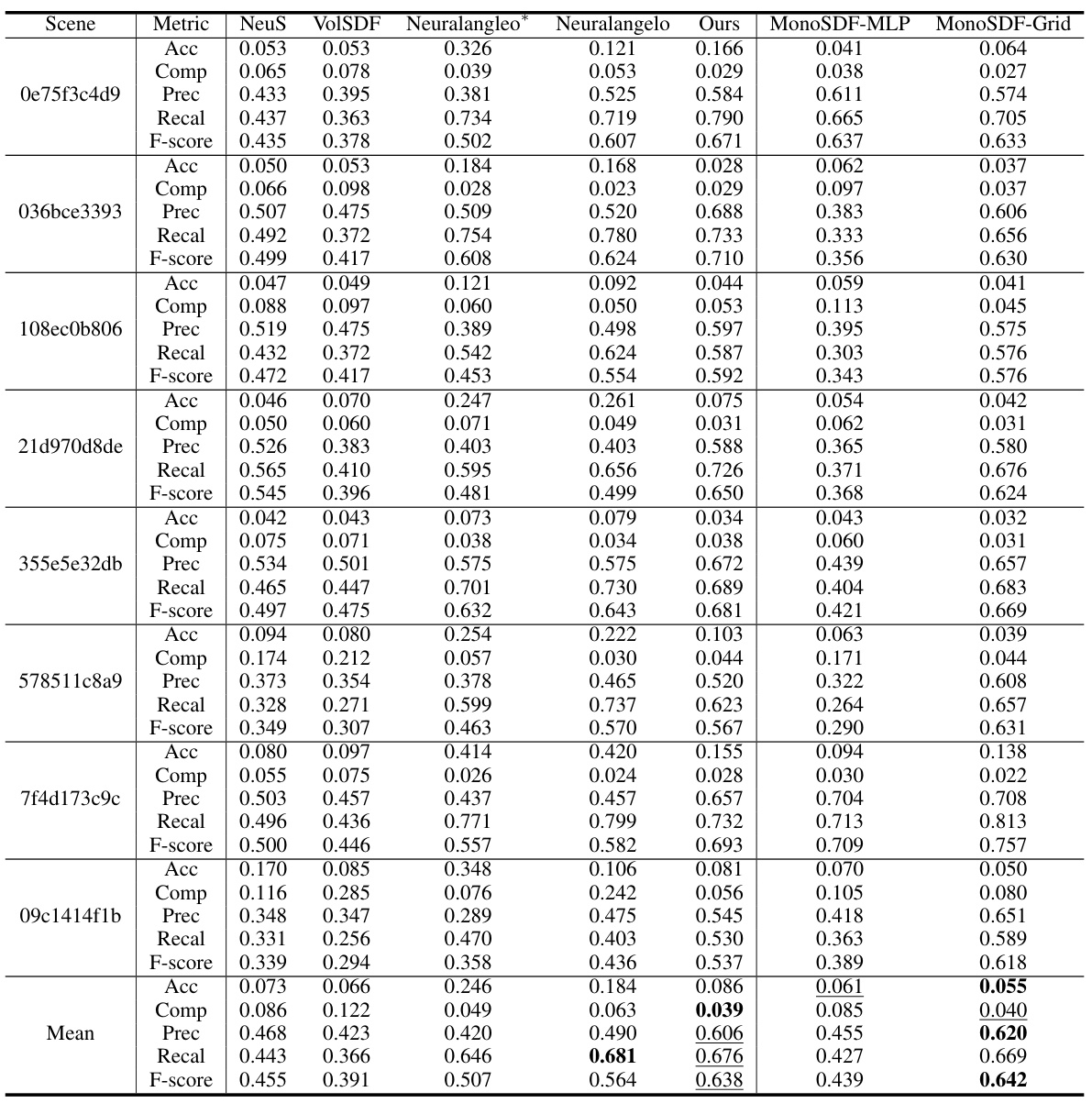
This table presents a quantitative comparison of the proposed NeuRodin method against several state-of-the-art techniques on the Tanks and Temples training dataset subset. The F-score metric is used to evaluate the performance of each method in reconstructing 3D surfaces. The table highlights the best and second-best results for easier comparison, and it notes that the NeuRodin method uses the same hash grid parameters as the Neuralangelo method.
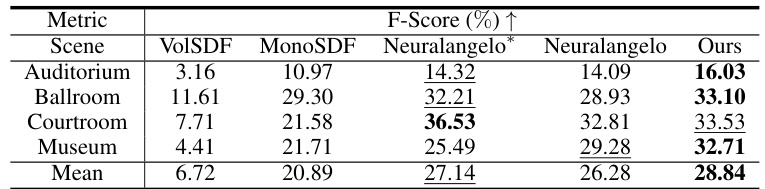
This table presents a quantitative comparison of the proposed NeuRodin method against several state-of-the-art techniques on the Tanks and Temples training dataset subset. The F-score metric is used to evaluate the accuracy of 3D surface reconstruction. The table highlights the best and second-best performing methods for each scene, indicating NeuRodin’s superior performance. It also notes that the hash grid parameters used in NeuRodin match those of Neuralangelo.

This table presents a quantitative comparison of the proposed NeuRodin method against several state-of-the-art techniques on a subset of the Tanks and Temples dataset. The metrics used for evaluation are F-score, a measure of surface reconstruction accuracy. The table highlights the best and second-best performing methods for each scene, facilitating easy comparison and emphasizing the relative performance of NeuRodin. The note clarifies that the hash grid parameters were kept consistent with Neuralangelo for a fair comparison.
This table presents a quantitative comparison of the proposed NeuRodin method against several state-of-the-art techniques on the Tanks and Temples training subset. The evaluation metric used is the F-score, which measures the accuracy of surface reconstruction. The table highlights the best and second-best performing methods for each scene in the dataset. Notably, the NeuRodin method uses the same hash grid parameters as Neuralangelo, a key competitor.

This table presents a quantitative comparison of the proposed NeuRodin method against several state-of-the-art techniques on the Tanks and Temples training subset. The evaluation metric is the F-score, a measure of the accuracy of 3D surface reconstruction. The table highlights the best and second-best performing methods for each scene, demonstrating NeuRodin’s superior performance. Note that the hash grid parameters used in NeuRodin are identical to Neuralangelo.

This table presents a quantitative comparison of the proposed NeuRodin method against several state-of-the-art methods on the Tanks and Temples training subset. The evaluation metric is the F-score, a measure of the accuracy of 3D surface reconstruction. The table shows that NeuRodin achieves the best performance overall, significantly outperforming other methods in multiple scenes. Notably, it highlights that NeuRodin uses the same hash grid parameters as Neuralangelo, implying a fair comparison.

This table presents a quantitative comparison of the proposed NeuRodin method against several state-of-the-art techniques on the Tanks and Temples training subset. The evaluation metric used is the F-score, a measure of the accuracy of 3D surface reconstruction. The table highlights the best and second-best performing methods for each scene, demonstrating NeuRodin’s superiority. It also notes that the hash grid parameters used in NeuRodin are identical to those in Neuralangelo, providing context for the comparison.
Full paper#