↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Traditional methods for tubular structure extraction, like blood vessel or road network segmentation, often struggle with accurately restoring topology due to their pixel-level approach. These methods frequently produce errors such as broken or redundant branches. This limitation necessitates a more sophisticated method that prioritizes accurate topological representation.
GraphMorph tackles this challenge by focusing on branch-level features. It leverages a Graph Decoder to generate a graph that captures the tubular structure, and a Morph Module that uses a novel SkeletonDijkstra algorithm to create a centerline mask aligned with the graph. This two-step process results in improved accuracy, reducing false positives and negatives. Furthermore, a simple post-processing step enhances segmentation accuracy by using the generated centerline mask to filter out false positives. The study demonstrates GraphMorph’s effectiveness across various datasets, making it a significant advancement in tubular structure extraction.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel approach to tubular structure extraction that significantly improves topological accuracy. This is a crucial advancement for various applications, including medical image analysis and urban planning, where accurate topology is essential for reliable interpretation and decision-making. The GraphMorph method and its post-processing strategy offer a new avenue for improving accuracy and efficiency in similar tasks, opening possibilities for new research directions.
Visual Insights#
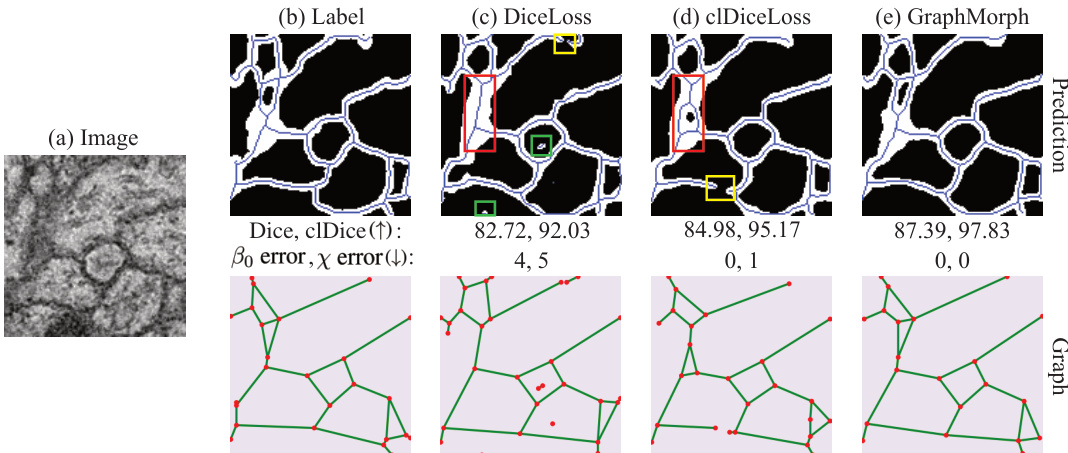
This figure compares the performance of GraphMorph against two other methods on a neuron image segmentation task. It highlights the importance of using topological features for accurate segmentation by showing how GraphMorph avoids common errors like broken or extra branches, resulting in improved accuracy metrics (Dice, clDice, β0 error, x error).
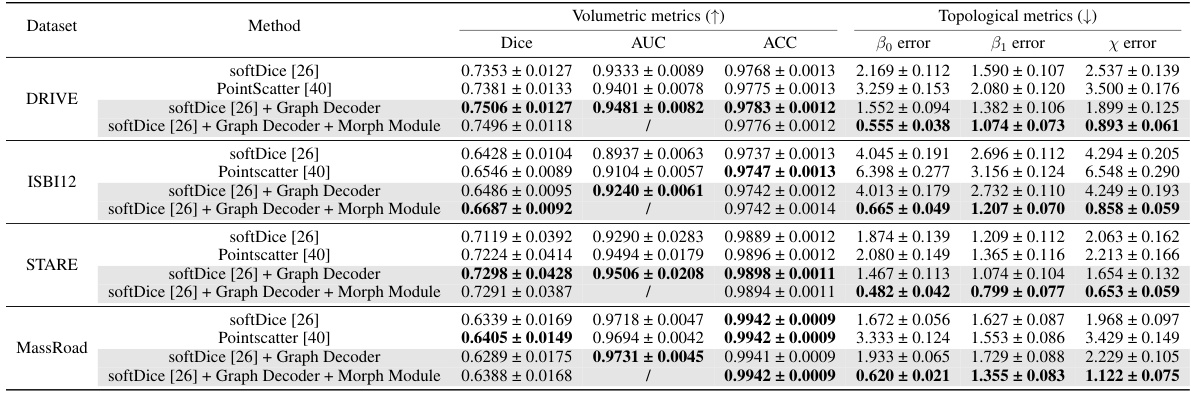
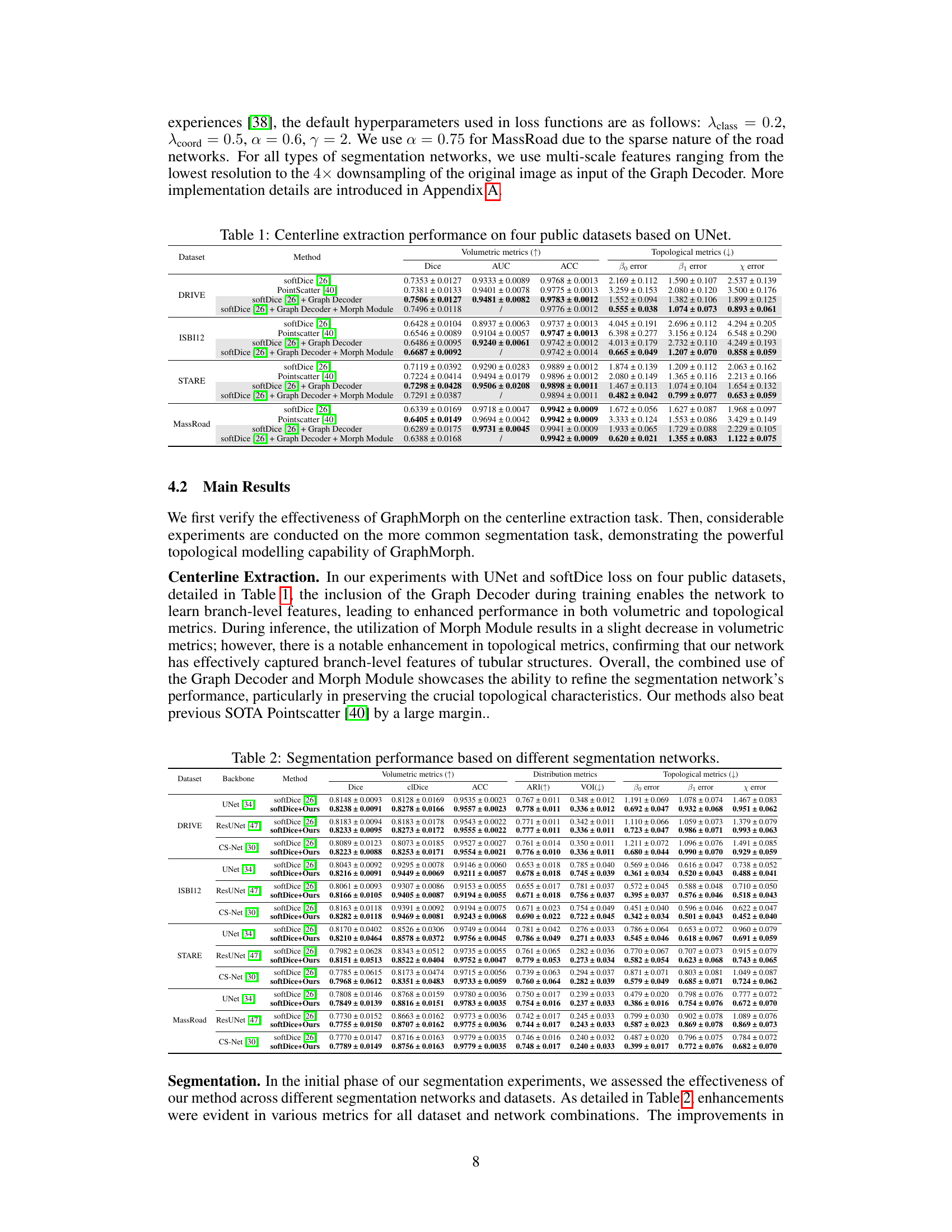
This table presents a comparison of centerline extraction performance using the UNet model across four datasets: DRIVE, STARE, ISBI12, and MassRoad. The table shows the results for several methods, including: softDice [26], PointScatter [40], softDice [26] + Graph Decoder, and softDice [26] + Graph Decoder + Morph Module. For each method, the table provides several metrics: Dice, AUC, ACC, β0 error, β1 error, and χ error. These metrics assess both volumetric and topological aspects of the results, providing a comprehensive evaluation of the methods’ accuracy and effectiveness.
In-depth insights#
Topological Accuracy#
In the context of tubular structure extraction, topological accuracy refers to the algorithm’s ability to correctly represent the connectivity and branching patterns of the structures. Traditional pixel-level methods often struggle with this, leading to errors such as broken branches (false negatives), extra branches (false positives), and incorrect topological relationships. Graph-based approaches offer a potential solution, as they explicitly model the structure’s topology. However, challenges remain in ensuring the predicted graph accurately reflects the true underlying structure and that the process of extracting the final centerline mask or segmentation from the graph preserves this accuracy. The use of branch-level features and novel algorithms like the SkeletonDijkstra algorithm, as employed in GraphMorph, aim to enhance this accuracy by concentrating on crucial branch endpoints and connections. The effectiveness of these methods is ultimately assessed by evaluating topological metrics such as the number of broken or extra branches, ensuring the algorithm captures the true structural complexity. Post-processing steps can further improve accuracy by refining the initial centerline extraction or segmentation, and the success is measured by the degree to which the final results accurately reflect the inherent topology of the tubular structures.
Graph-Based Method#
A graph-based method leverages the power of graph theory to represent and analyze data, particularly useful when dealing with complex relationships and structures. This approach moves beyond traditional pixel-level or feature-based methods by explicitly modeling the connections and dependencies between data points as nodes and edges in a graph. This representation allows for the capture of higher-order interactions and global context, leading to more accurate and robust results, especially in tasks like tubular structure extraction where topological accuracy is critical. Graph-based methods excel at handling complex topological relationships, which are often poorly captured by other techniques. The utilization of multi-scale features and advanced graph algorithms allows for the extraction of meaningful patterns from complex image data. A key advantage lies in its ability to address the challenges posed by noise and artifacts in images, offering enhanced robustness to data imperfections. However, the success of this method hinges heavily on the appropriate choice of graph construction techniques, feature extraction strategies, and the selection of suitable graph algorithms, which must be tailored to the specific application and data characteristics. Careful consideration of computational costs and memory requirements is also essential, particularly when working with large graphs. Although powerful, designing robust and efficient graph-based methods requires significant expertise in graph theory and related algorithmic techniques.
Morph Module’s Role#
The Morph Module plays a crucial role in GraphMorph by bridging the gap between predicted graphs and topologically accurate centerline masks. It leverages both the graph structure and a centerline probability map as input to its novel SkeletonDijkstra algorithm. This algorithm efficiently finds optimal paths between graph nodes, effectively suppressing false positives (redundant branches) and false negatives (broken branches) inherent in simpler centerline extraction methods. The restriction to single-pixel width paths during pathfinding guarantees topological accuracy, directly addressing a primary limitation of pixel-level approaches. The Morph Module’s output, a refined centerline mask, serves as an effective post-processing tool, significantly improving segmentation results by reducing false positives. Overall, the Morph Module’s training-free nature and topological awareness make it a core component in GraphMorph’s success at accurate tubular structure extraction.
Future Research#
Future research directions stemming from this GraphMorph work could focus on several key areas. Improving the efficiency of the Morph Module is crucial; its current reliance on a sliding window and CPU processing makes it computationally expensive. Exploring parallel processing strategies or developing alternative algorithms for centerline extraction are vital. Another key area involves enhancing the robustness of GraphMorph to noisy or incomplete data. The algorithm’s performance might degrade with poor-quality segmentation maps, necessitating further research on noise-handling techniques and data augmentation strategies to increase resilience. Finally, extending GraphMorph to handle more complex topological structures and 3D data would broaden its applicability. Current limitations hinder accurate prediction in densely packed or highly intertwined tubular networks, a challenge that requires innovative architectural adaptations and possibly the incorporation of more advanced graph neural network techniques. Furthermore, integrating GraphMorph with other computer vision tasks, such as image registration or tracking, could unlock synergistic benefits.
Method Limitations#
A thoughtful analysis of a research paper’s limitations section, particularly concerning its methodology, should go beyond a simple listing of flaws. It should delve into the impact of those limitations on the study’s overall conclusions and broader implications. For instance, a limitation such as the use of a specific dataset might be examined in terms of its generalizability to other contexts. The analysis should explore if the limitations affect the validity of the core claims and whether the acknowledged limitations are adequately addressed in the paper’s methodology. A robust assessment also involves exploring any unstated or overlooked limitations that could undermine the study’s reliability and suggests further research to strengthen the study’s robustness. The discussion should focus on how the limitations potentially affect reproducibility and whether proposed solutions are sufficiently detailed to enable verification by others. A strong analysis will evaluate the degree to which the presented limitations impact the practical applicability of the findings.
More visual insights#
More on figures

This figure illustrates the training process of GraphMorph. It shows how a segmentation network processes an input image, generating a probability map and multi-scale feature maps. Regions of interest (ROIs) are sampled, and their features are fed into a Graph Decoder (using a modified Deformable DETR). The Graph Decoder predicts nodes within the ROIs and their adjacency matrices using a link prediction module. The training process involves pixel-wise, bipartite matching, and weighted-BCE losses.
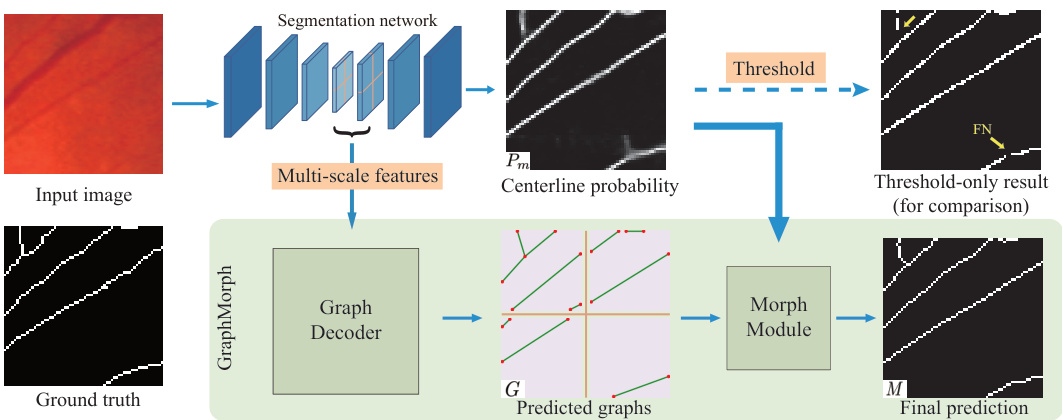
This figure illustrates the inference process of centerline extraction in the GraphMorph method. It starts with a segmentation network producing a centerline probability map and multi-scale features. These features are fed into a Graph Decoder, which uses a sliding window approach to predict graphs representing the tubular structures in the image. Finally, the predicted graphs and probability map are combined in the Morph Module to generate a final, topologically accurate centerline mask. The final result is contrasted with a simpler thresholding approach to highlight the improved topological accuracy of GraphMorph.
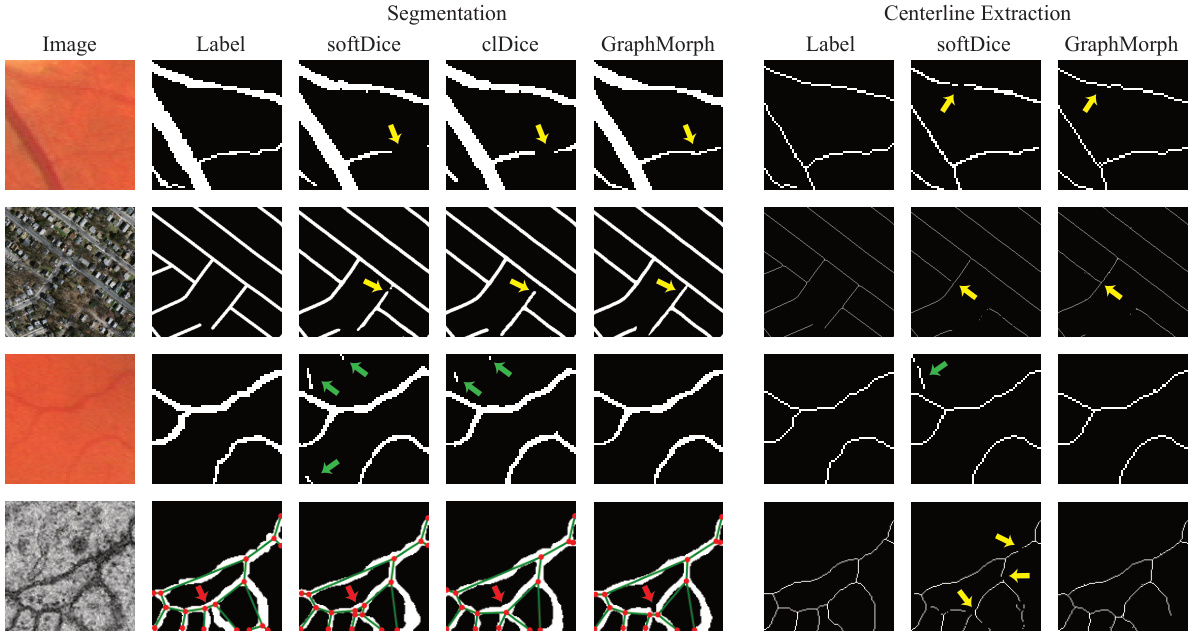
This figure provides a visual comparison of GraphMorph’s performance against other methods on the segmentation and centerline extraction tasks. It highlights specific examples where GraphMorph successfully addresses false negatives (missing parts of the structure), false positives (incorrectly identified parts), and topological errors (incorrect connections or branchings). The yellow, green, and red arrows point to the specific errors that are corrected by the GraphMorph method.
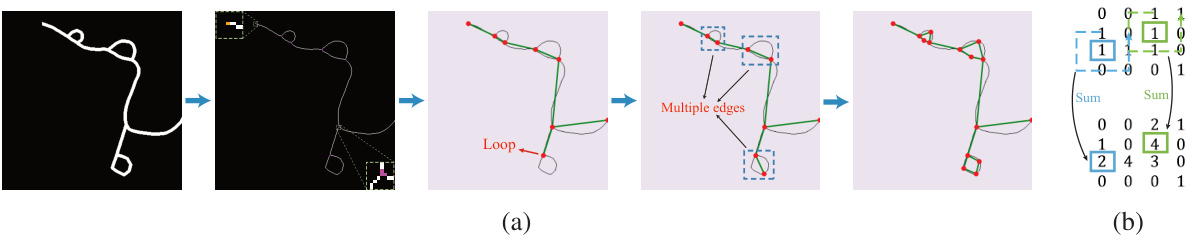
This figure shows the steps involved in constructing a graph from a binary mask of a road network. It starts with skeletonization, then identifies endpoints and junctions, merges nearby junctions, and finally resolves loops and multiple edges to create a simplified graph suitable for efficient processing. The subfigure (b) demonstrates how the number of neighbouring centerline points (N) is calculated for each point.

This figure demonstrates the importance of considering topology in tubular structure segmentation. It compares the results of GraphMorph with two other methods that don’t explicitly model topology. The figure shows that GraphMorph significantly improves segmentation accuracy by learning branch-level features and reducing topological errors, such as broken or redundant branches.

This figure visualizes the intermediate steps in the centerline extraction process using GraphMorph. It compares the results of GraphMorph with a simpler thresholding method. The top four rows show that GraphMorph improves results by morphing predicted graphs; however, the bottom two rows illustrate that inaccurate probability maps can cause GraphMorph to miss some true positives.
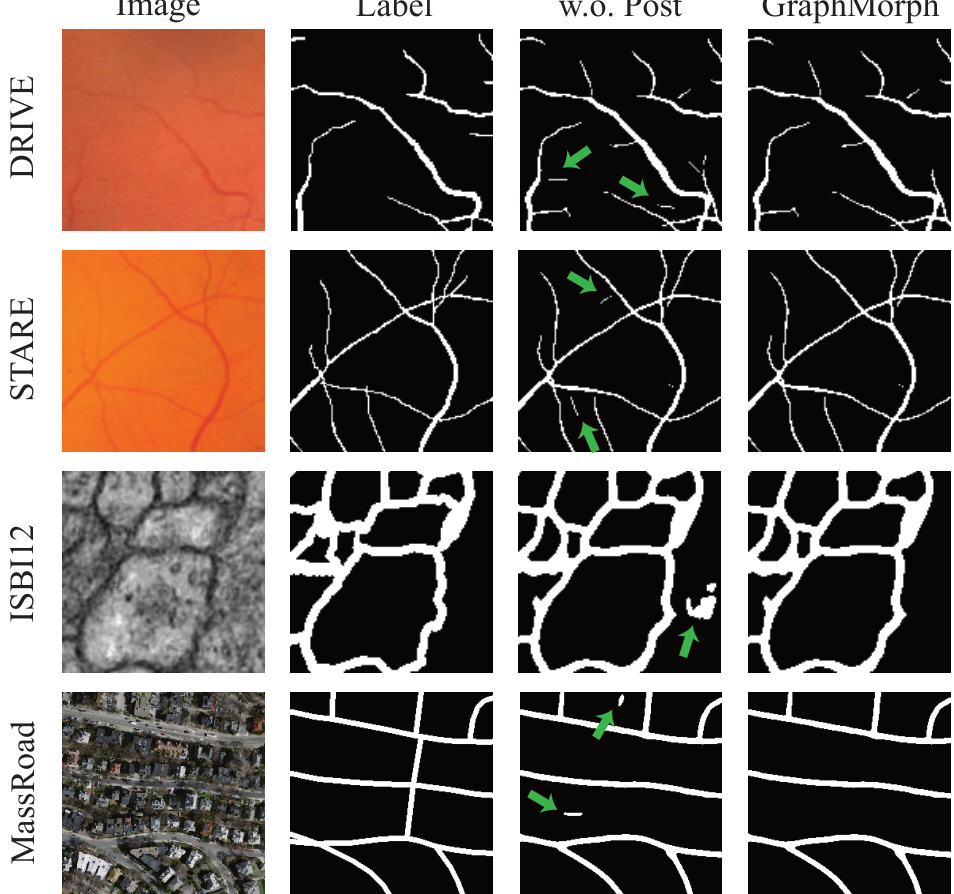
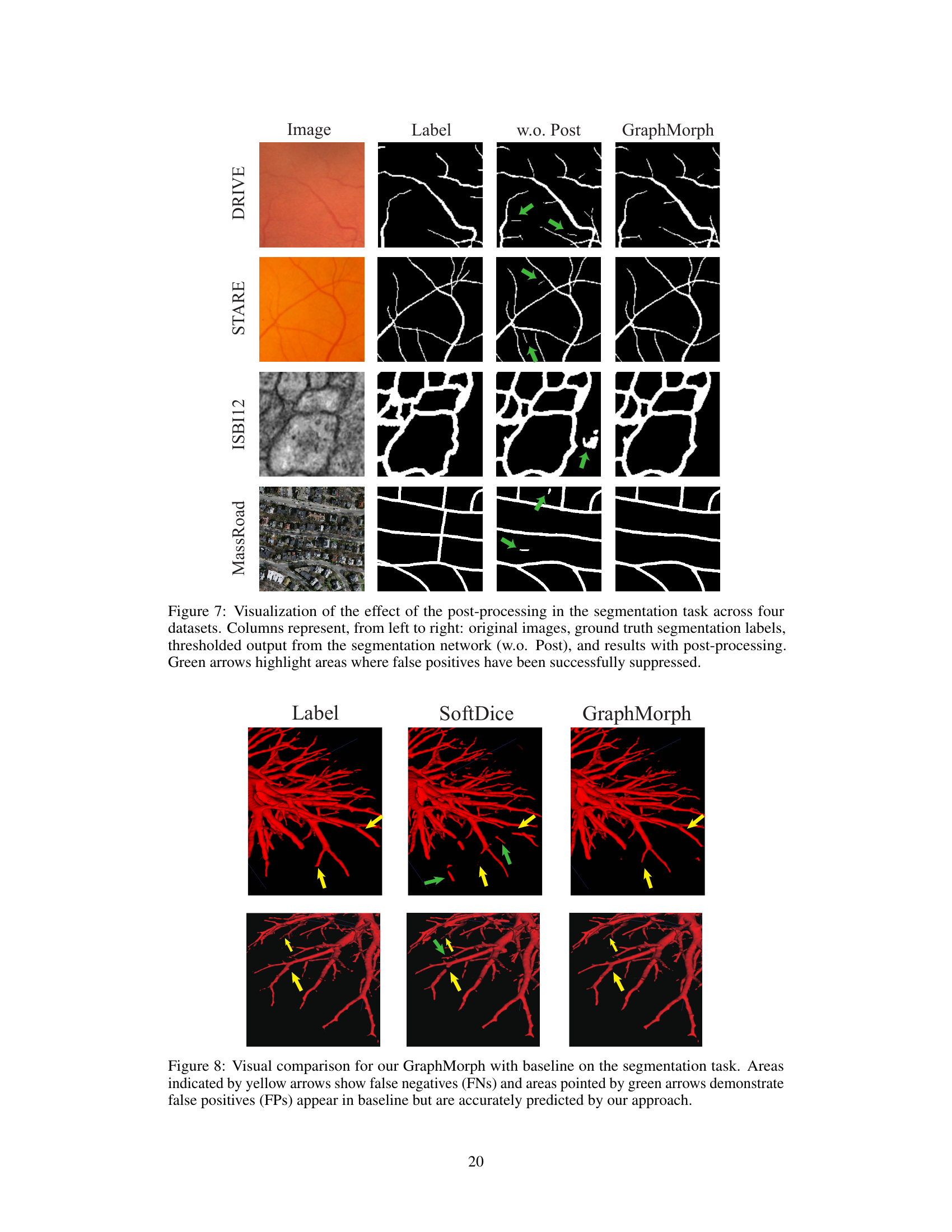
This figure shows a comparison of segmentation results with and without the post-processing step applied in GraphMorph. Four datasets are used for the comparison: DRIVE, STARE, ISBI12, and MassRoad. For each dataset, the figure shows the original image, the ground truth segmentation, the results obtained without the post-processing step (using a simple threshold), and the final results produced by GraphMorph, which incorporates a post-processing step to suppress false positives. Green arrows highlight areas where the post-processing successfully removes false positive predictions.
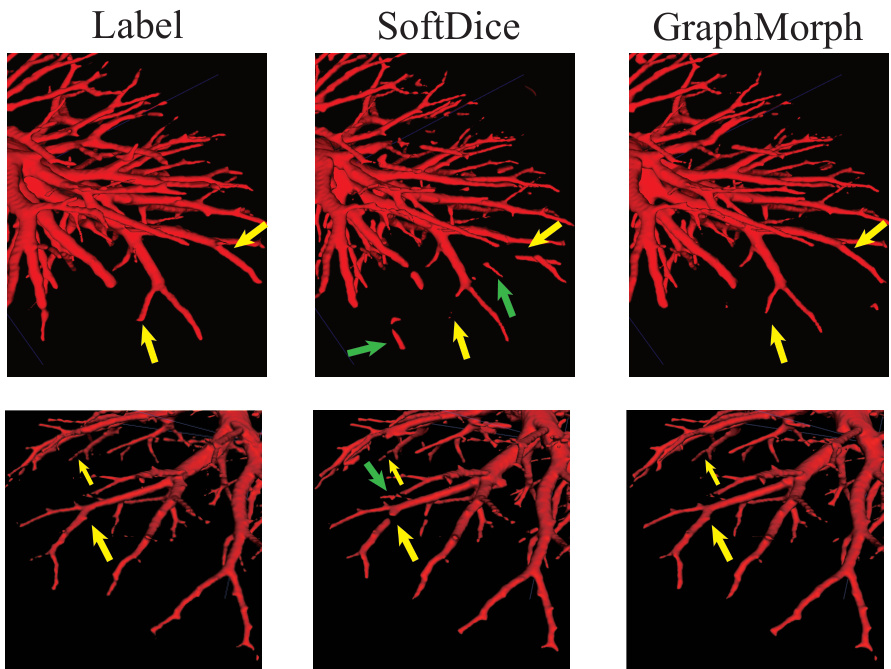
This figure compares the segmentation results of GraphMorph and a baseline method (SoftDice) on a sample image. Yellow arrows highlight areas where the baseline method missed parts of the tubular structure (false negatives), while green arrows point to regions where the baseline incorrectly identified non-tubular regions as part of the structure (false positives). The image shows that GraphMorph more accurately identifies the tubular structure, reducing both false negatives and false positives.
More on tables
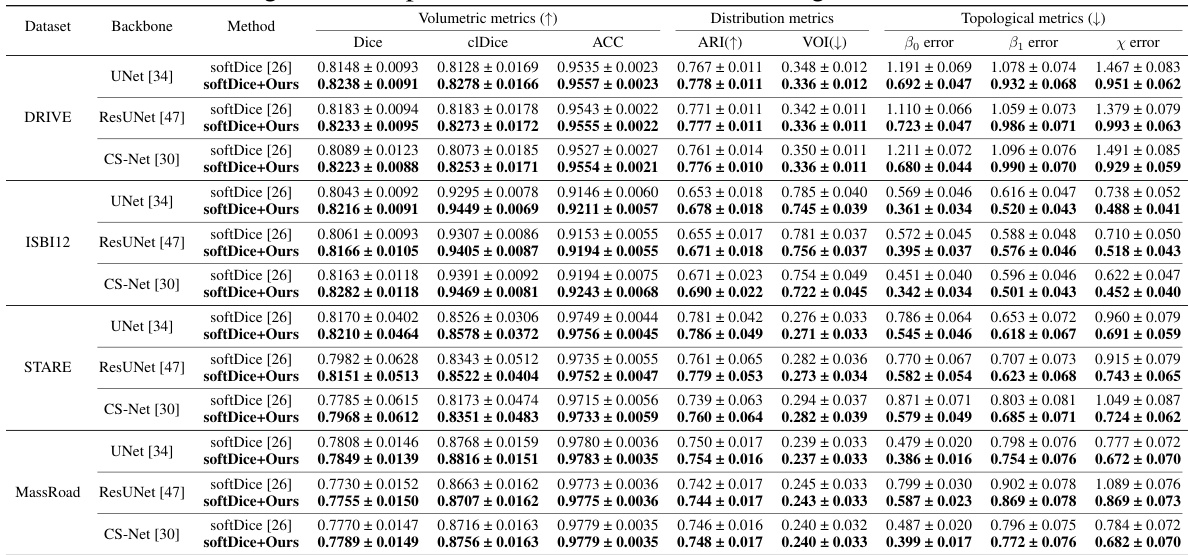
This table presents a comparison of the segmentation performance achieved by using GraphMorph in conjunction with different segmentation network backbones (UNet, ResUNet, and CS-Net). It shows the improvement in volumetric metrics (Dice, clDice, ACC) and topological metrics (Bo error, B1 error, and X error) when GraphMorph is added to the standard softDice loss function. The results are presented across four different datasets (DRIVE, ISBI12, STARE, and MassRoad). The table demonstrates the consistent improvement obtained by integrating GraphMorph into the various network backbones, showcasing its general applicability and effectiveness.
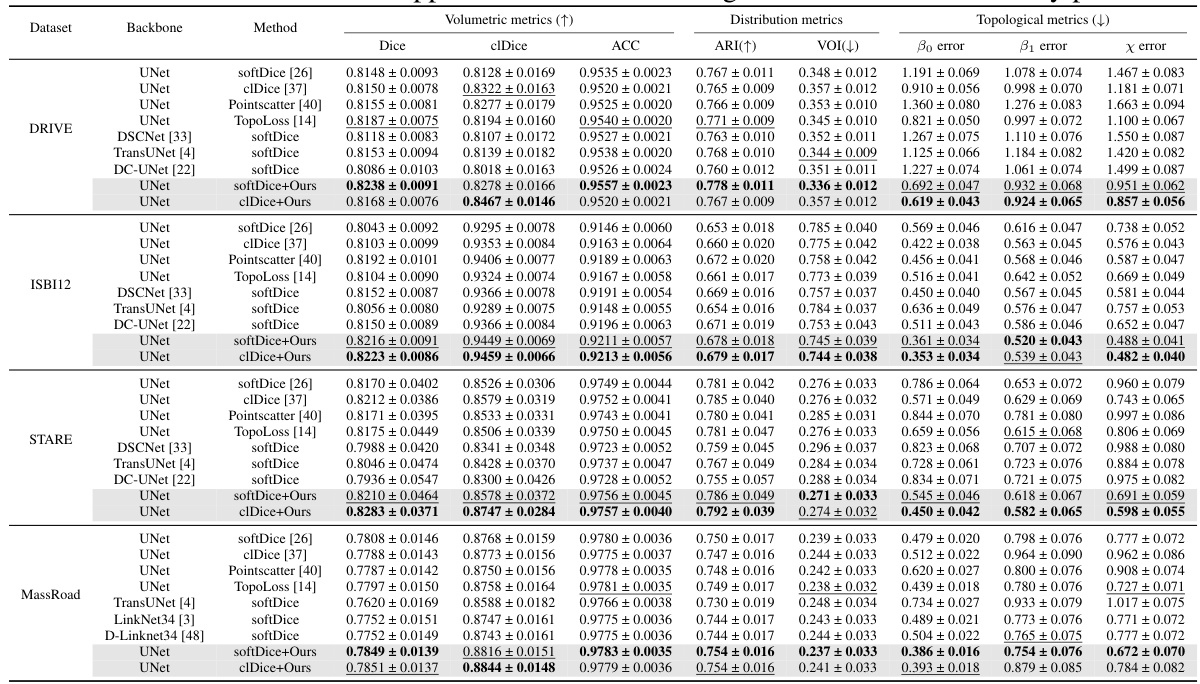
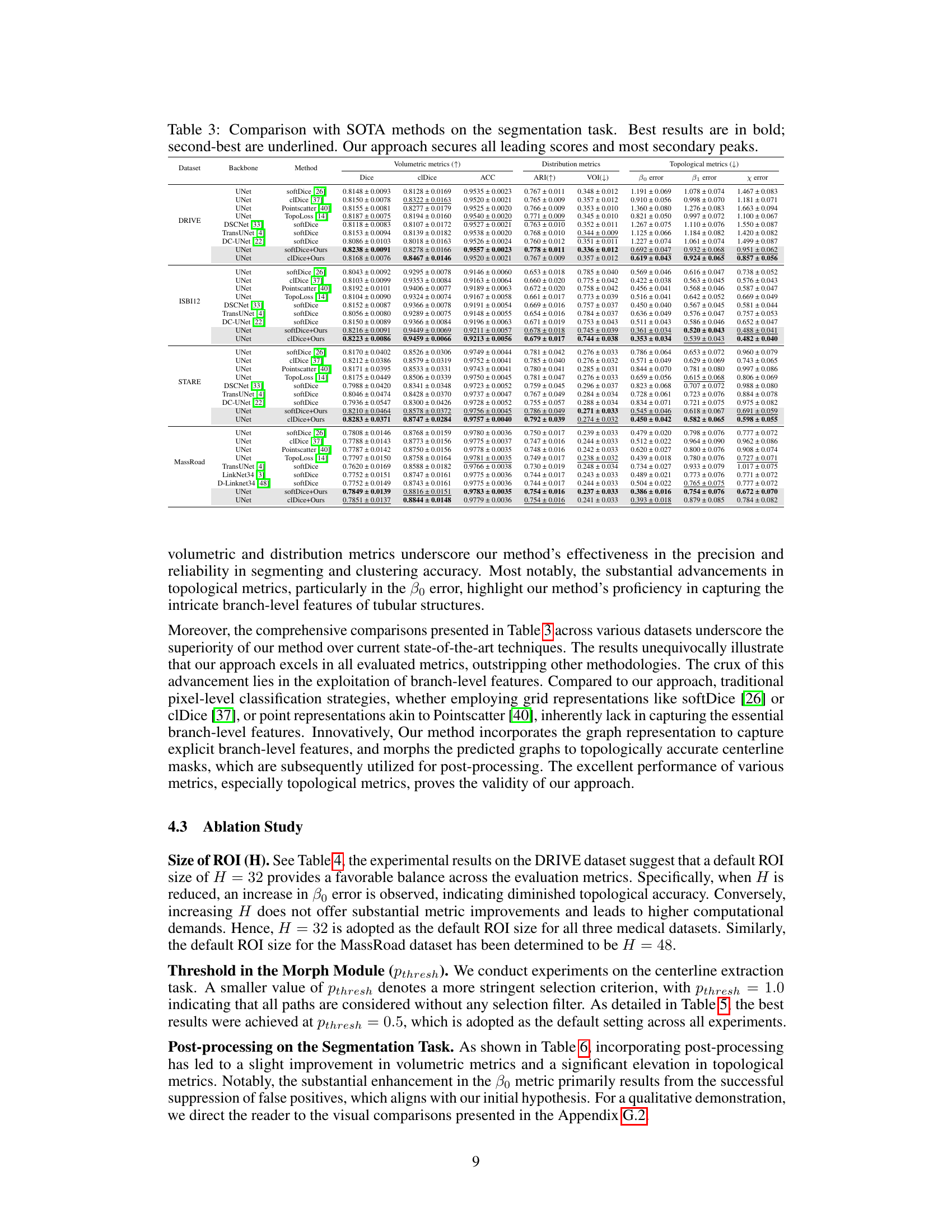
This table compares the performance of GraphMorph against several state-of-the-art (SOTA) methods on four different datasets for the image segmentation task. The metrics used include Dice, clDice, ACC, ARI, VOI, and topological error metrics (β0 error, β1 error, χ error). The table shows that GraphMorph consistently outperforms other methods across all datasets and metrics, achieving the best scores (in bold) and most of the second-best scores (underlined). This demonstrates the effectiveness of GraphMorph in achieving high-precision and high-reliability image segmentation results.
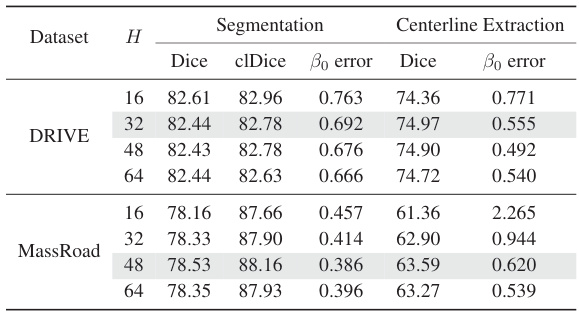
This table presents the results of experiments conducted to determine the optimal size of the Region of Interest (ROI) for both the segmentation and centerline extraction tasks. Different ROI sizes (H) were tested, and the table shows the impact on various metrics, including Dice coefficient, clDice, β₀ error (a measure of topological errors), and Accuracy (ACC). The results help determine the optimal ROI size that balances performance and computational cost.
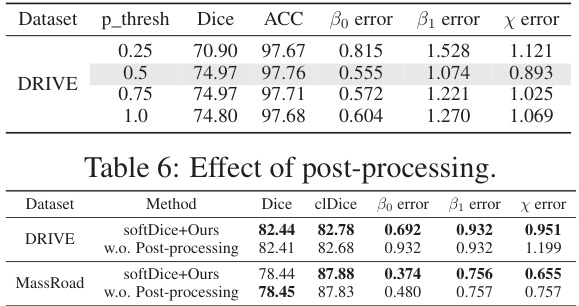
This table demonstrates the impact of post-processing on the segmentation task using two different methods, softDice+Ours and without post-processing. It shows the Dice, clDice, Bo error, B1 error, and x error for both methods on two datasets: DRIVE and MassRoad. The results indicate the improvement in metrics after applying post-processing, particularly a significant reduction in false positives.

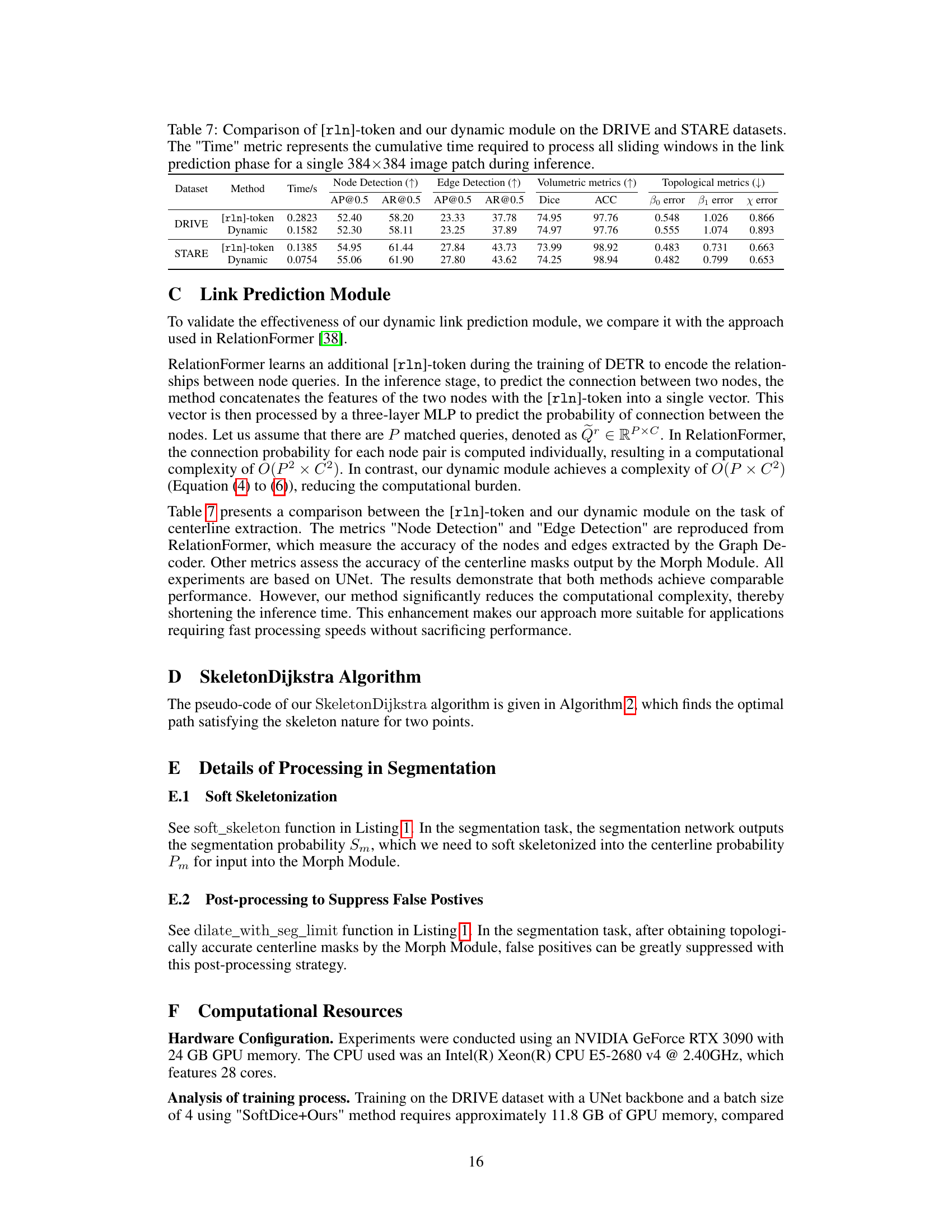
This table compares the performance of RelationFormer’s [rln]-token approach and the proposed dynamic link prediction module in terms of time efficiency and accuracy. The comparison is done on two datasets, DRIVE and STARE. The metrics include time taken for link prediction, node detection performance (AP@0.5 and AR@0.5), edge detection performance (AP@0.5 and AR@0.5), volumetric metrics (Dice and ACC), and topological metrics (B0 error, B1 error, and X error). The results show that the dynamic module achieves comparable performance to the [rln]-token approach but with significantly reduced computational complexity.

This table compares the computational resources required for training two different methods: SoftDice and softDice+Ours. The softDice+Ours method, which incorporates the GraphMorph framework, uses significantly more parameters and FLOPs (floating point operations), leading to a longer training time per iteration and higher GPU memory consumption.
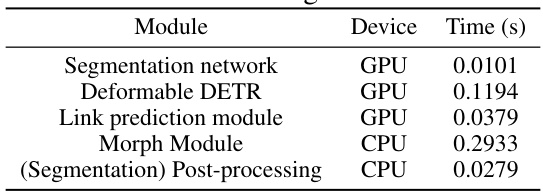
This table presents the inference time for each module in the GraphMorph pipeline. The inference time is measured in seconds for a single 384x384 image patch from the DRIVE dataset, with H=32 and stride=30 for the sliding window. The Morph Module is the most time-consuming step, and the authors suggest that parallelization of this step could significantly improve efficiency.

This table presents the quantitative results of GraphMorph on the PARSE dataset, a 3D dataset for pulmonary arterial vascular segmentation. It compares the performance of the standard softDice loss with the proposed GraphMorph method using UNet as the backbone. The evaluation metrics include volumetric metrics (Dice, clDice, ACC), distribution metrics (ARI, VOI), and topological metrics (β₀ error, χ error). The results demonstrate that GraphMorph significantly improves performance across all metrics, highlighting its effectiveness in 3D segmentation tasks.
Full paper#