TL;DR#
Offline reinforcement learning (RL) faces challenges with distribution shift and overestimation of Q-values, especially when dealing with limited and noisy datasets. Existing diffusion-based methods, despite their high expressiveness, often suffer from these issues. This limitation hinders the development of robust and reliable RL agents that can generalize well to unseen situations.
This paper presents a novel approach to address these limitations. It proposes an entropy-regularized diffusion policy that uses a mean-reverting stochastic differential equation to sample actions. This policy increases exploration of out-of-distribution samples. Further, the approach incorporates Q-ensembles for more reliable Q-value prediction, improving the reliability and stability of training. The results showcase superior performance on the D4RL benchmark tasks, demonstrating the effectiveness of the proposed method.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in offline reinforcement learning as it introduces a novel entropy-regularized diffusion policy significantly improving performance on benchmark tasks. It tackles the crucial challenge of overestimating Q-values on out-of-distribution data, opening avenues for more robust and reliable offline RL agents. The proposed method combines entropy regularization and Q-ensembles resulting in state-of-the-art results, advancing the field and inspiring further research on handling uncertainty and improving exploration in offline RL settings.
Visual Insights#
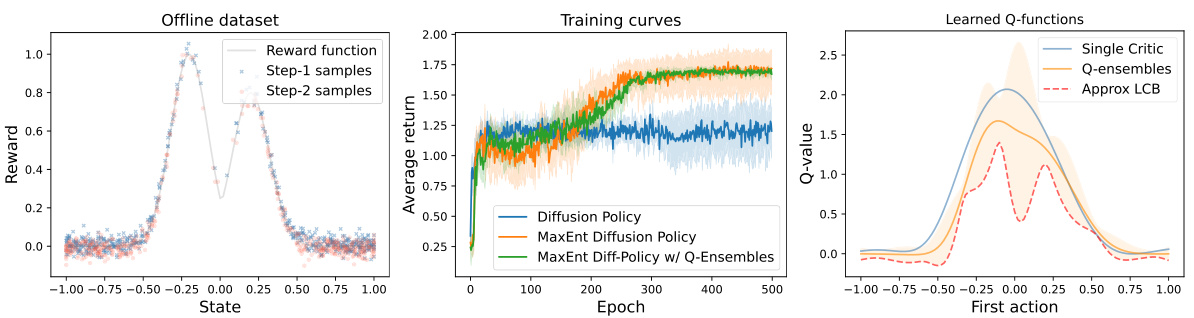
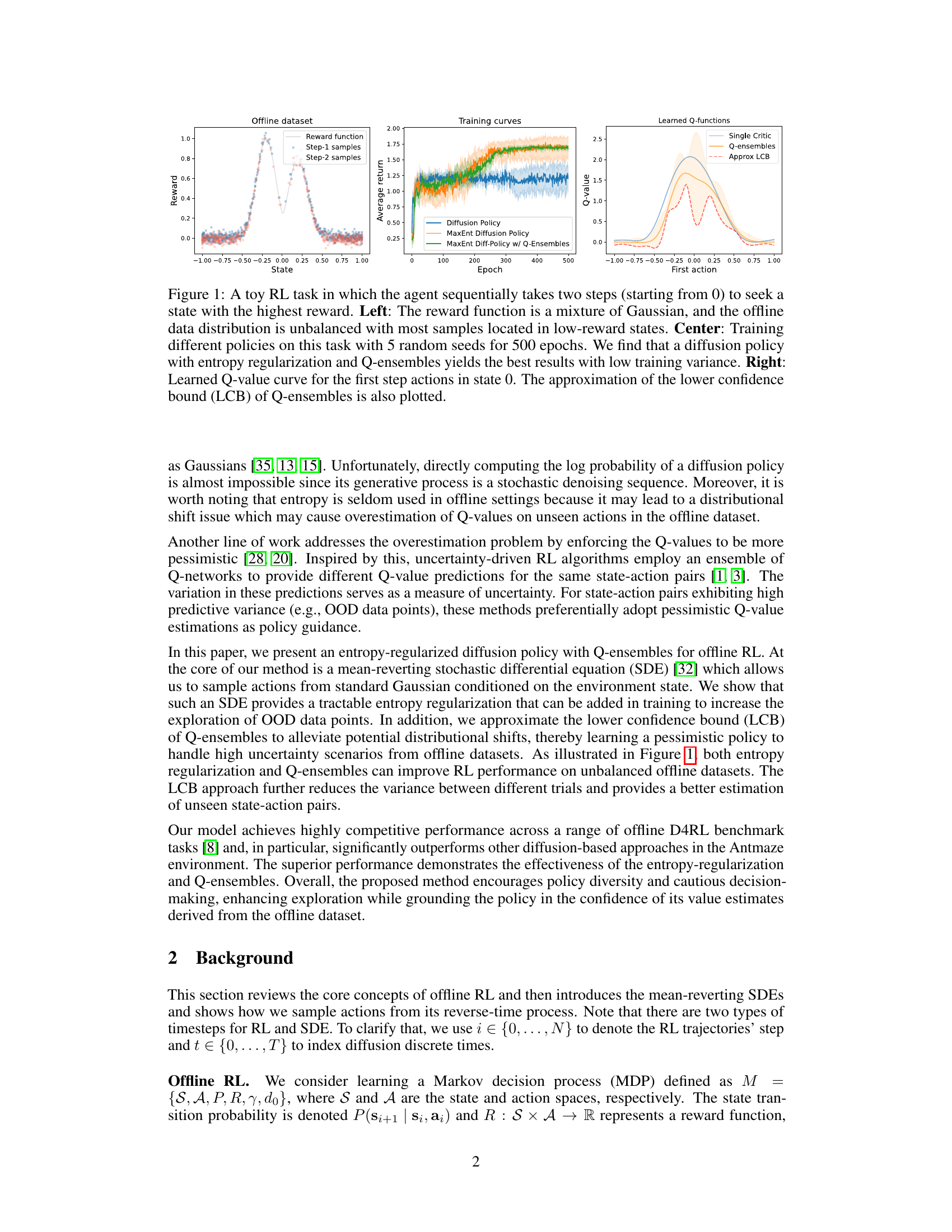
🔼 This figure shows a simple reinforcement learning task where an agent needs to move from state 0 to a high reward state in two steps. The reward function is a mixture of Gaussians, and the offline dataset is imbalanced (more samples in low-reward states). The figure compares three different offline RL policies trained for 500 epochs: a standard diffusion policy, a diffusion policy with entropy regularization, and a diffusion policy with both entropy regularization and Q-ensembles. The results show that adding entropy regularization and Q-ensembles significantly improves the performance and reduces the variance across different random seeds. Finally, the Q-value functions learned by the different methods are compared to illustrate the benefits of using Q-ensembles and approximating their lower confidence bound (LCB) for more pessimistic Q-value estimation.
read the caption
Figure 1: A toy RL task in which the agent sequentially takes two steps (starting from 0) to seek a state with the highest reward. Left: The reward function is a mixture of Gaussian, and the offline data distribution is unbalanced with most samples located in low-reward states. Center: Training different policies on this task with 5 random seeds for 500 epochs. We find that a diffusion policy with entropy regularization and Q-ensembles yields the best results with low training variance. Right: Learned Q-value curve for the first step actions in state 0. The approximation of the lower confidence bound (LCB) of Q-ensembles is also plotted.

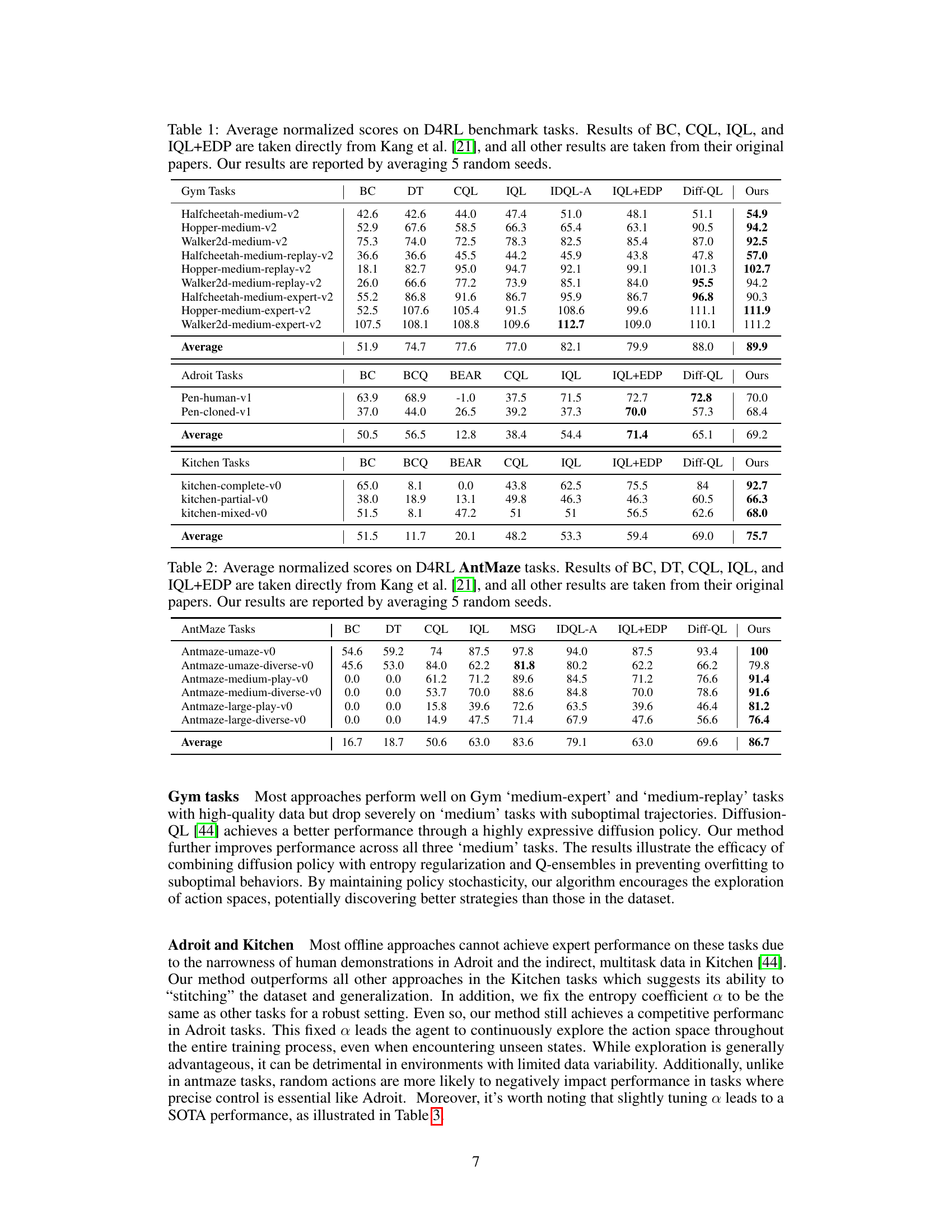
🔼 This table presents a comparison of the average normalized scores achieved by various offline reinforcement learning methods on four different D4RL benchmark domains (Gym, AntMaze, Adroit, and Kitchen). The table includes both existing methods from literature and the proposed method from this paper. The scores represent the average performance across multiple random seeds, providing a robust comparison across different algorithms and tasks.
read the caption
Table 1: Average normalized scores on D4RL benchmark tasks. Results of BC, CQL, IQL, and IQL+EDP are taken directly from Kang et al. [21], and all other results are taken from their original papers. Our results are reported by averaging 5 random seeds.
In-depth insights#
MaxEnt Diffusion#
MaxEnt Diffusion, a fascinating concept, blends the power of maximum entropy principles with diffusion models. Maximum entropy ensures exploration by maximizing the uncertainty in the agent’s actions, crucial for offline reinforcement learning where interactions are limited. Diffusion models, known for their excellent function approximation and generation capabilities, provide a natural framework to implement such exploration. By combining them, MaxEnt Diffusion likely results in a policy that is both expressive (able to capture complex behavior) and robust (less prone to overfitting the limited offline data). The use of entropy allows for a principled approach to balance exploration and exploitation, addressing the crucial challenge of effective learning from a fixed dataset. This approach likely offers advantages over simpler methods that rely on heuristic exploration strategies, potentially leading to better performance on challenging offline RL tasks, especially in scenarios with sparse rewards and highly uncertain dynamics.
Q-Ensemble LCB#
The concept of “Q-Ensemble LCB” combines the advantages of Q-ensembles and lower confidence bounds (LCB) for improved offline reinforcement learning. Q-ensembles offer a more robust and less overconfident estimate of the Q-function by averaging the predictions of multiple independent Q-networks. This helps address the common issue of overestimation in offline RL, where the trained model might incorrectly predict high rewards for actions never seen before in the training dataset. The LCB then takes this ensemble of Q-function estimates and selects the most pessimistic estimate—the lowest value within the confidence interval—as a more conservative policy guide. This pessimistic approach further mitigates overestimation bias and promotes safer and more reliable policy learning. The combination of Q-ensembles and LCB leverages the strengths of both techniques: reducing overestimation by using an ensemble and increasing exploration via the pessimistic LCB approach, ultimately enhancing the stability and performance of offline reinforcement learning agents, particularly in scenarios with noisy or limited data. This cautious strategy prevents the agent from overly relying on potentially inaccurate Q-value estimates, leading to more reliable and robust performance.
D4RL Benchmarks#
The D4RL (Datasets for Deep Data-driven Reinforcement Learning) benchmark suite plays a crucial role in evaluating offline reinforcement learning algorithms. Its diverse collection of datasets, encompassing various robotic tasks and difficulty levels (e.g., Gym, AntMaze, Adroit, Kitchen), allows for comprehensive assessment of algorithm performance across different complexities. The inclusion of both low- and high-quality datasets (suboptimal to expert demonstrations) highlights an algorithm’s robustness to dataset quality and the ability to extrapolate to unseen data. Furthermore, the varied characteristics of the datasets—in terms of state-action distributions and reward sparsity—are essential in exposing weaknesses in algorithms, especially those relying on specific assumptions about data distribution. Performance on D4RL benchmarks effectively serves as a standard measure of progress in offline reinforcement learning, enabling researchers to compare their methods against existing state-of-the-art approaches and identify future research directions.
Offline RL Exp.#
Offline reinforcement learning (RL) experiments are crucial for evaluating the effectiveness of algorithms trained on pre-collected datasets without online interaction. A core challenge is the distribution shift, where the data used for training may not accurately represent the states and actions encountered during deployment. Effective offline RL methods must address this by incorporating techniques such as behavior cloning, conservative Q-learning, or entropy regularization. In offline RL experiments, key metrics include the cumulative reward achieved by the learned policy, the sample efficiency of the learning process, and the robustness of the policy to unseen situations or out-of-distribution data. Careful consideration should be given to the selection of benchmark datasets, including the data diversity and representativeness, to allow fair and reliable evaluation of different offline RL algorithms. A good offline RL experiment design carefully considers factors such as the evaluation environment, number of trials, random seeds for reproducibility, and statistical significance testing to ensure robust and reliable results. The success of an offline RL algorithm ultimately hinges upon its ability to generalize to unseen conditions, making rigorous experimental validation essential.
Future Works#
The paper concludes by highlighting several promising avenues for future research. A key area is improving the computational efficiency of the proposed method, particularly for deployment on resource-constrained devices. The authors acknowledge that real-time performance is a significant limitation and plan to investigate real-time policy distillation techniques. Further exploration of hyperparameter optimization strategies is also warranted, potentially using automated methods for tuning entropy regularization and the LCB coefficient to enhance robustness and performance across diverse tasks. Finally, extending the model’s adaptability to a broader range of offline RL benchmarks and exploring alternative methods for managing uncertainty and distributional shift would further strengthen the work’s impact.
More visual insights#
More on figures
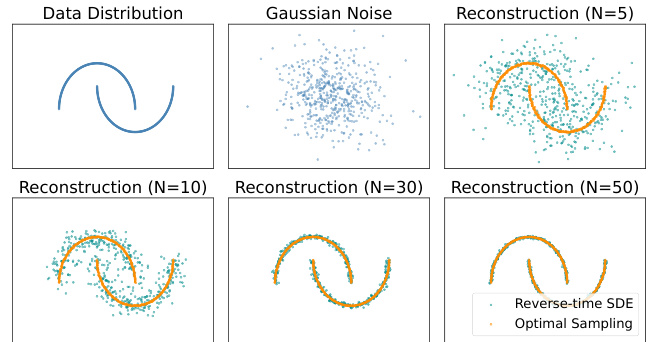
🔼 This figure compares the performance of the standard reverse-time stochastic differential equation (SDE) process and the proposed optimal sampling method for reconstructing data. The top row shows the original data distribution, Gaussian noise, and reconstruction using the reverse-time SDE with 5 diffusion steps. The bottom row shows reconstructions using the reverse-time SDE and the optimal sampling method with increasing numbers of diffusion steps (10, 30, and 50). The orange line represents the true data distribution, while the teal points represent the generated samples. The figure demonstrates that the optimal sampling method converges more quickly and efficiently to the true distribution, requiring fewer steps to achieve accurate reconstruction.
read the caption
Figure 2: Comparison of the reverse-time SDE and optimal sampling process in data reconstruction.
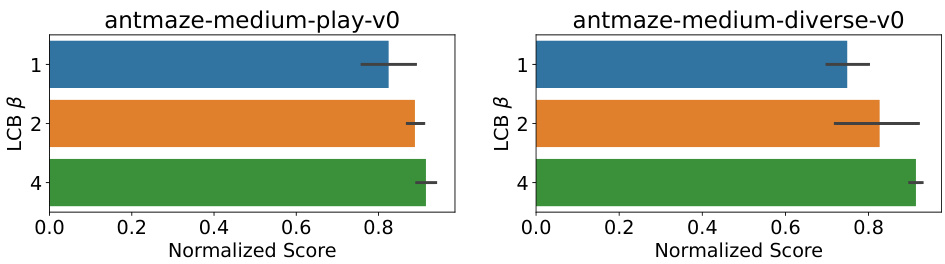
🔼 This figure presents the results of ablation studies conducted to evaluate the impact of different LCB (Lower Confidence Bound) coefficient values (β = 1, 2, and 4) on the performance of the proposed method. The experiments were performed on AntMaze-Medium environments, and the results are averaged across 5 different random seeds. The figure visually demonstrates how the choice of β influences the normalized score achieved by the model. This helps in understanding the impact of the level of pessimism introduced by the Q-ensembles on the exploration-exploitation balance and overall performance.
read the caption
Figure 3: Ablation experiments of our method with different values of LCB coefficient β = 1,2, 4 on AntMaze-Medium environments over 5 different random seeds.
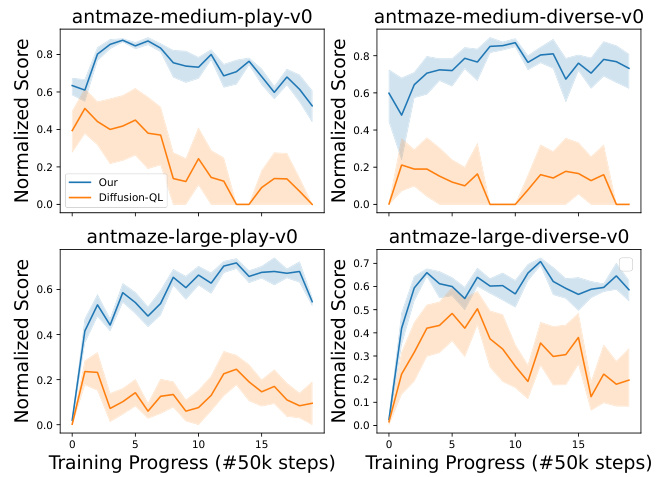
🔼 This figure displays the training progress curves for both the Diffusion-QL method and the proposed method (referred to as ‘Our’ in the legend) on four different AntMaze tasks. Each curve represents the average normalized score across five random seeds, providing a measure of the stability and performance consistency of each approach. The shaded regions surrounding the lines indicate the standard deviation of the scores across the five runs. The figure shows that the proposed method exhibits more stable and consistent learning compared to Diffusion-QL, particularly in the later stages of training, resulting in higher average scores.
read the caption
Figure 4: Learning curves of the Diffusion-QL and our method on selected AntMaze tasks over 5 random seeds.
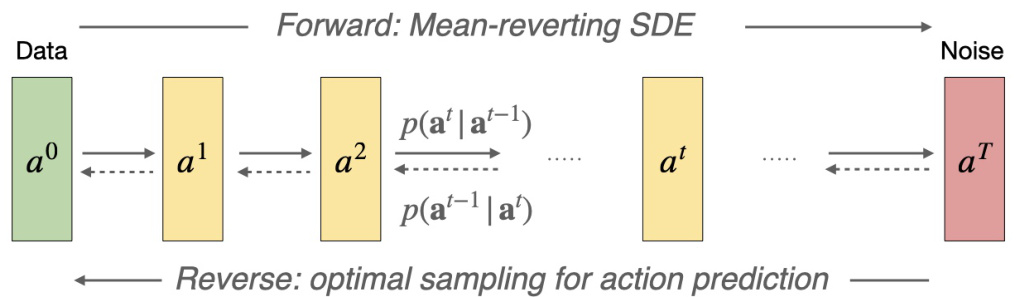
🔼 This figure illustrates the forward and reverse processes of the mean-reverting stochastic differential equation (SDE) used for action prediction in the proposed method. The forward process shows how actions from the dataset are gradually degraded to pure noise through the SDE. The reverse process, which is crucial for action generation, samples actions from the noise by reversing the time of the SDE. This reversed process is conditioned on the current environment state and guided by the lower confidence bound (LCB) of the Q-ensembles, ensuring that the generated actions are grounded in the estimated value function while encouraging exploration of unseen action spaces.
read the caption
Figure 5: Visualization of the workings of the mean-reverting SDE for action prediction. The SDE models the degradation process from the action from the dataset to a noise. By guiding the policy with corresponding reverse-time SDE and the LCB of Q, a new action is generated conditioned on the RL state.

🔼 This figure compares the performance of the standard reverse-time SDE process and the proposed optimal sampling method for reconstructing data. It shows that the optimal sampling method achieves faster convergence with fewer steps (N=5) compared to the reverse-time SDE (N=30, N=50). The figure visually demonstrates the efficiency of the proposed method, highlighting its advantage in terms of sample efficiency.
read the caption
Figure 2: Comparison of the reverse-time SDE and optimal sampling process in data reconstruction.
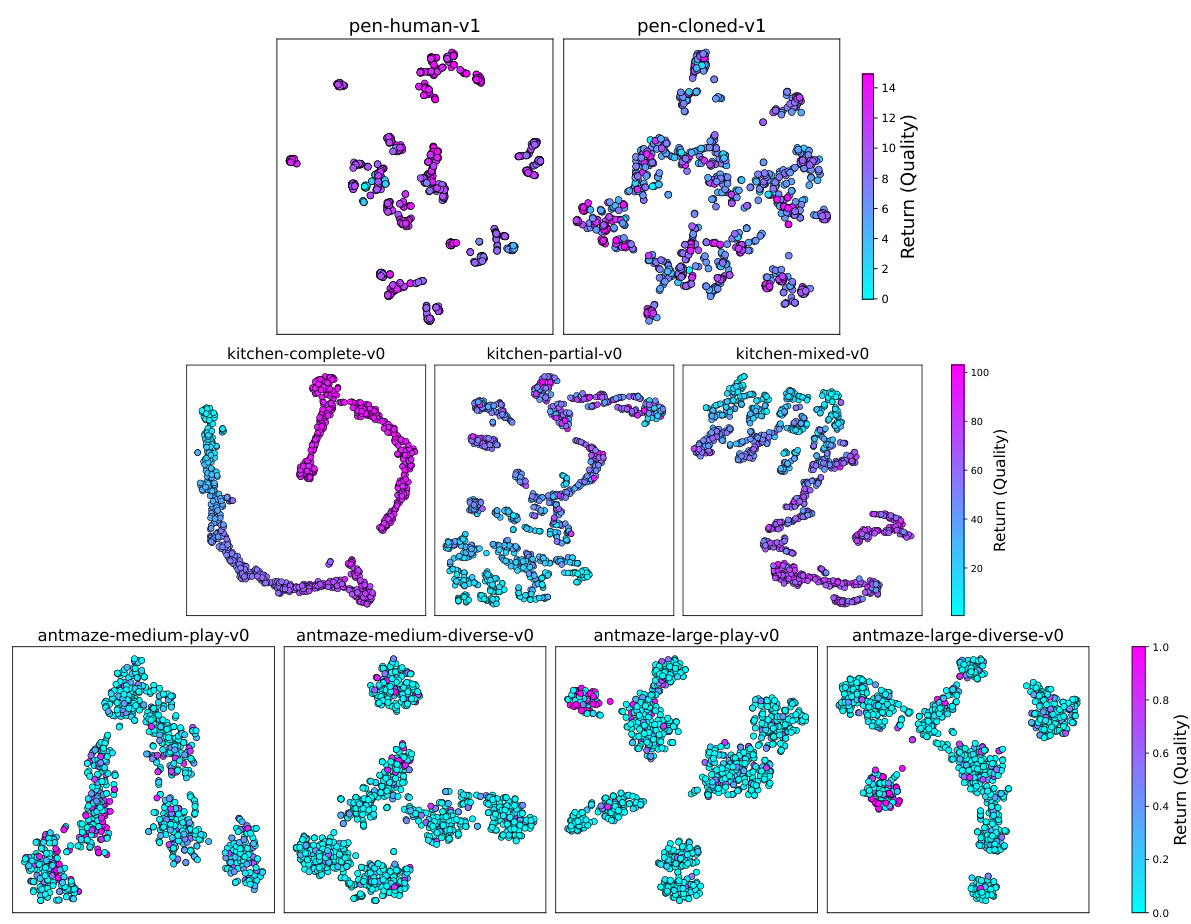
🔼 This figure uses t-SNE to visualize 1000 randomly sampled states from three different D4RL benchmark domains: AntMaze, Adroit, and Kitchen. Each point represents a state, and its color indicates the cumulative reward obtained from that state. The visualization helps to understand the distribution of states and their associated rewards within each domain, providing insights into the complexity and characteristics of the environments.
read the caption
Figure 7: A t-SNE visualization of randomly selected 1000 states from Antmaze, Adroit and Kitchen domain. The color coding represents the return of the trajectory associated with each state.

🔼 This figure shows a simple RL task where an agent takes two steps to reach a high-reward state. The reward function is a mixture of Gaussians, and the offline dataset has an imbalanced distribution with more samples in low-reward areas. Three subplots illustrate the reward function, training curves for different policies, and learned Q-values with confidence bounds. The results demonstrate the superiority of a diffusion policy using entropy regularization and Q-ensembles, achieving better performance and lower training variance.
read the caption
Figure 1: A toy RL task in which the agent sequentially takes two steps (starting from 0) to seek a state with the highest reward. Left: The reward function is a mixture of Gaussian, and the offline data distribution is unbalanced with most samples located in low-reward states. Center: Training different policies on this task with 5 random seeds for 500 epochs. We find that a diffusion policy with entropy regularization and Q-ensembles yields the best results with low training variance. Right: Learned Q-value curve for the first step actions in state 0. The approximation of the lower confidence bound (LCB) of Q-ensembles is also plotted.
More on tables
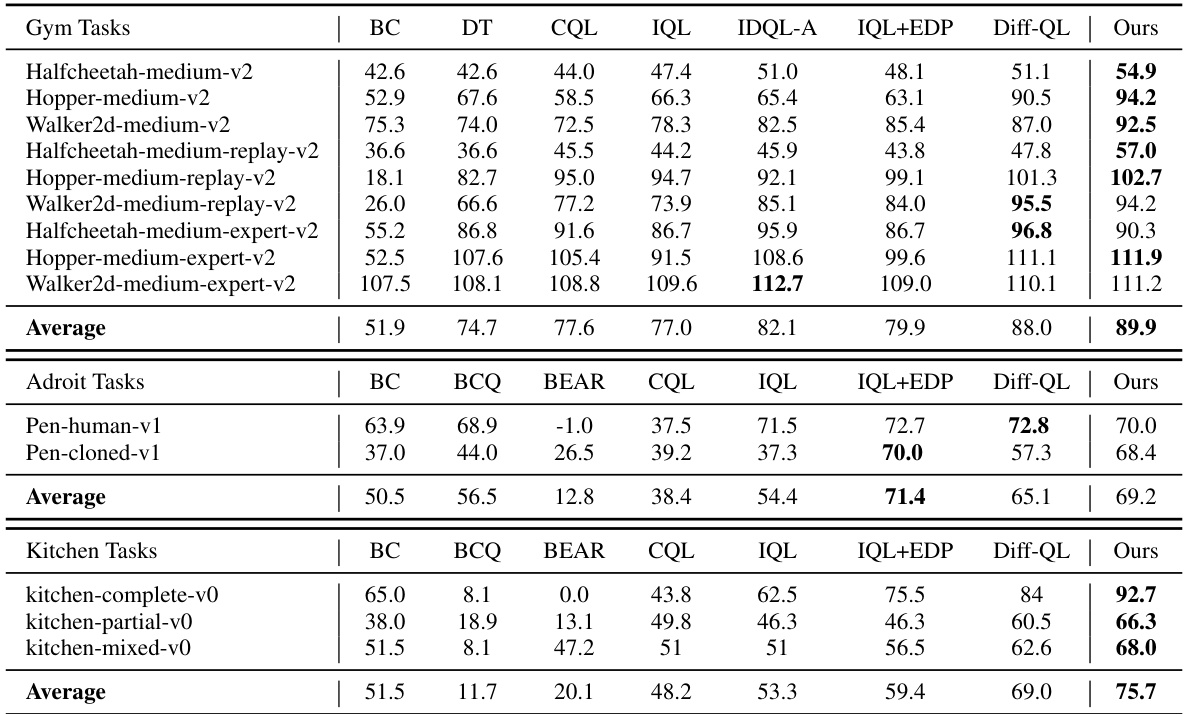
🔼 This table presents the average normalized scores achieved by various offline reinforcement learning methods across multiple benchmark tasks from the D4RL dataset. The methods compared include behavior cloning (BC), conservative Q-learning (CQL), Implicit Q-learning (IQL), IQL with efficient diffusion policies (IQL+EDP), Diffusion-QL, and the proposed method in the paper. The results are averaged across five independent random seeds to ensure statistical reliability. The table is broken down by task category (Gym, Adroit, Kitchen) to allow for easier comparison of performance within each task type.
read the caption
Table 1: Average normalized scores on D4RL benchmark tasks. Results of BC, CQL, IQL, and IQL+EDP are taken directly from Kang et al. [21], and all other results are taken from their original papers. Our results are reported by averaging 5 random seeds.
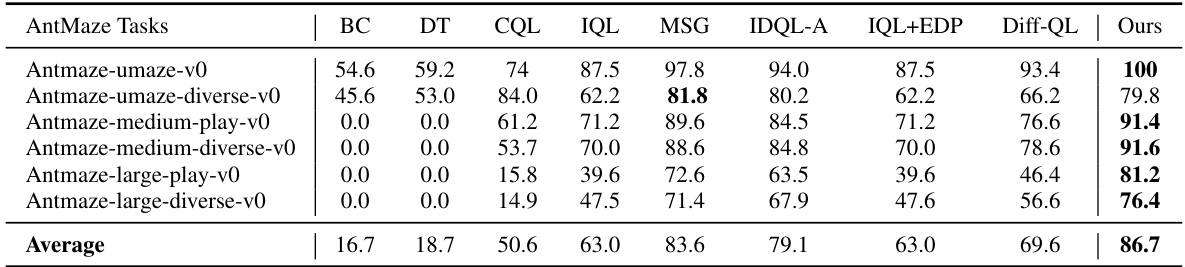
🔼 This table presents the average normalized scores achieved by various offline reinforcement learning methods on AntMaze tasks from the D4RL benchmark. It compares the proposed method’s performance against several baselines, including behavior cloning, conservative Q-learning, and other diffusion-based approaches. The results are averaged across five random seeds to assess the statistical significance and robustness of the methods.
read the caption
Table 2: Average normalized scores on D4RL AntMaze tasks. Results of BC, DT, CQL, IQL, and IQL+EDP are taken directly from Kang et al. [21], and all other results are taken from their original papers. Our results are reported by averaging 5 random seeds.
🔼 This table presents the average normalized scores achieved by various offline reinforcement learning methods on four benchmark datasets (Gym, AntMaze, Adroit, and Kitchen) from the D4RL benchmark. The table compares the performance of the proposed method against several state-of-the-art baselines, highlighting the improvement in performance achieved by the proposed approach. The results are averaged over five independent random seeds to provide a robust assessment.
read the caption
Table 1: Average normalized scores on D4RL benchmark tasks. Results of BC, CQL, IQL, and IQL+EDP are taken directly from Kang et al. [21], and all other results are taken from their original papers. Our results are reported by averaging 5 random seeds.
🔼 This table presents the average normalized scores achieved by different offline reinforcement learning algorithms on four AntMaze tasks from the D4RL benchmark. The algorithms compared include behavior cloning (BC), Decision Transformer (DT), Conservative Q-Learning (CQL), Implicit Q-Learning (IQL), IQL with Entropy-Regularized Diffusion Policy (IQL+EDP), Diffusion-QL, and the proposed method (Ours). The results are averaged over five random seeds to account for stochasticity. The table highlights the performance improvements achieved by the proposed method over existing state-of-the-art approaches.
read the caption
Table 2: Average normalized scores on D4RL AntMaze tasks. Results of BC, DT, CQL, IQL, and IQL+EDP are taken directly from Kang et al. [21], and all other results are taken from their original papers. Our results are reported by averaging 5 random seeds.
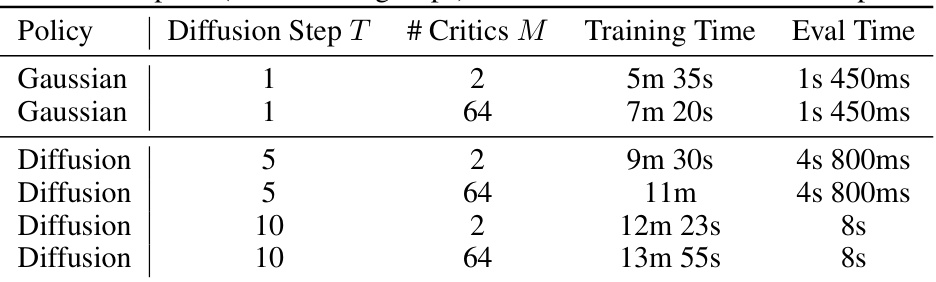
🔼 This table compares the training and evaluation times for different model configurations on the Antmaze-medium-play-v0 task. The configurations vary the number of diffusion steps (T), and the number of critics (M) used in the Q-ensemble. It shows how these parameters affect the time needed for both training and evaluation.
read the caption
Table 5: Computational time comparison with different settings on Antmaze-medium-play-v0. Training time is for 1 epoch (1000 training steps) and eval time is for 1000 RL steps.

🔼 This table presents a comparison of the average normalized scores achieved by different offline reinforcement learning methods on four benchmark datasets from D4RL (Gym, AntMaze, Adroit, and Kitchen). Each dataset includes multiple tasks, and the table shows the average performance across all tasks in each domain. The results for several baselines (BC, BCQ, BEAR, CQL, IQL, IQL+EDP, Diff-QL) are sourced directly from the referenced papers and are included for comparison. The ‘Ours’ column represents the results obtained using the method proposed in this paper, averaged over five independent training runs with different random seeds.
read the caption
Table 1: Average normalized scores on D4RL benchmark tasks. Results of BC, CQL, IQL, and IQL+EDP are taken directly from Kang et al. [21], and all other results are taken from their original papers. Our results are reported by averaging 5 random seeds.

🔼 This table presents the average normalized scores achieved by different offline reinforcement learning methods on four AntMaze tasks from the D4RL benchmark. The table compares the performance of the proposed method against several baselines, including behavior cloning (BC), Decision Transformer (DT), Conservative Q-learning (CQL), Implicit Q-learning (IQL), and IQL enhanced with an efficient diffusion policy (IQL+EDP). The scores are normalized and averaged over five random seeds to provide a robust comparison.
read the caption
Table 2: Average normalized scores on D4RL AntMaze tasks. Results of BC, DT, CQL, IQL, and IQL+EDP are taken directly from Kang et al. [21], and all other results are taken from their original papers. Our results are reported by averaging 5 random seeds.

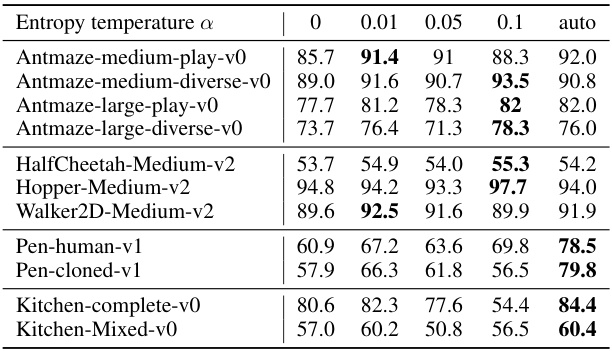
🔼 This table presents the ablation study results focusing on the impact of different LCB coefficients (β) on the AntMaze environment. It shows the average normalized scores and standard deviations for Antmaze-medium-play-v0 and Antmaze-medium-diverse-v0 tasks, with three different β values (1, 2, and 4). The average performance across both tasks is also provided for each β value.
read the caption
Table 8: Ablation study of LCB coefficients β.
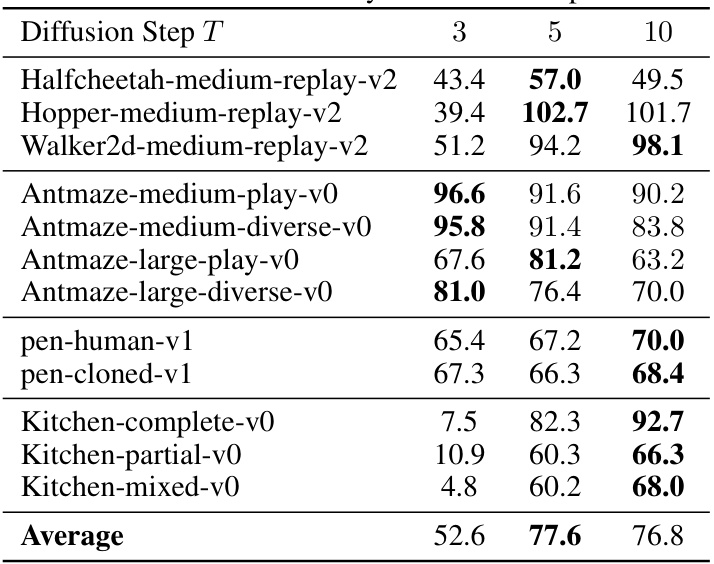
🔼 This table presents the ablation study results on varying the number of diffusion steps (T) for different tasks. It shows that while increasing the number of steps generally improves performance, five steps (T=5) provide the best balance across different tasks and between performance and computational time.
read the caption
Table 9: Ablation study of diffusion step T.

🔼 This table presents the ablation study results on the effect of using the Max Q-backup trick on AntMaze tasks. The results are presented as average normalized scores with standard deviations, comparing performance with and without the Max Q-backup technique across four different AntMaze environments.
read the caption
Table 10: Ablation study of 'Max Q trick'

🔼 This table presents a comparison of the average normalized scores achieved by various offline reinforcement learning methods on four different D4RL benchmark domains (Gym, AntMaze, Adroit, and Kitchen). The scores represent the performance of each algorithm on several tasks within each domain, showcasing the relative performance gains of the proposed method (Ours) compared to existing baselines. The results are averaged across five different random seeds to ensure statistical robustness.
read the caption
Table 1: Average normalized scores on D4RL benchmark tasks. Results of BC, CQL, IQL, and IQL+EDP are taken directly from Kang et al. [21], and all other results are taken from their original papers. Our results are reported by averaging 5 random seeds.
Full paper#