↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Training large AI models is computationally expensive and environmentally taxing. Current methods like low-precision training or matrix compression offer limited improvements. The high cost restricts access to this technology and creates environmental concerns.
CoMERA tackles this by employing rank-adaptive tensor optimization. It uses a multi-objective approach that balances compression and accuracy. CoMERA also features optimized GPU implementation to speed up computation. The results show CoMERA is significantly faster and more memory-efficient than existing methods, achieving speedups of 2-3x per training epoch and 9x memory efficiency improvement on tested models. This makes training large AI models more affordable and sustainable.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in AI and machine learning due to its focus on reducing the high computational costs associated with training large models. The proposed method, CoMERA, offers a novel approach to make training large AI models more accessible and environmentally friendly, and the findings have significant implications for the development of future AI systems. It opens new avenues for research in tensor compression techniques, GPU optimization strategies, and efficient training methods for large language models.
Visual Insights#
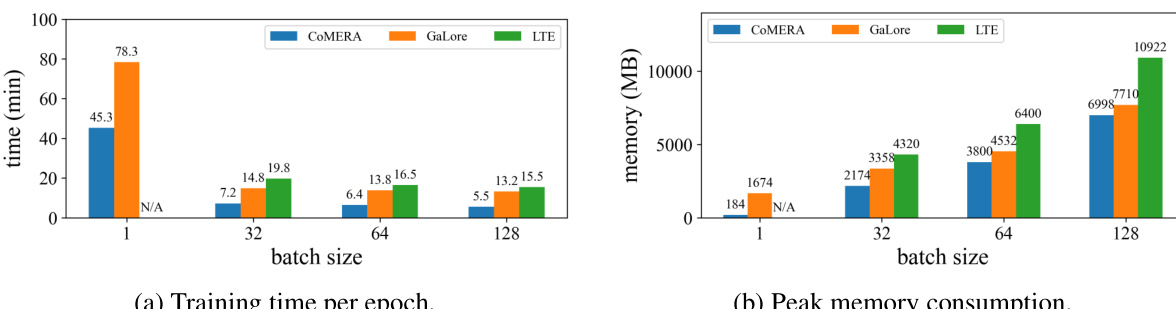
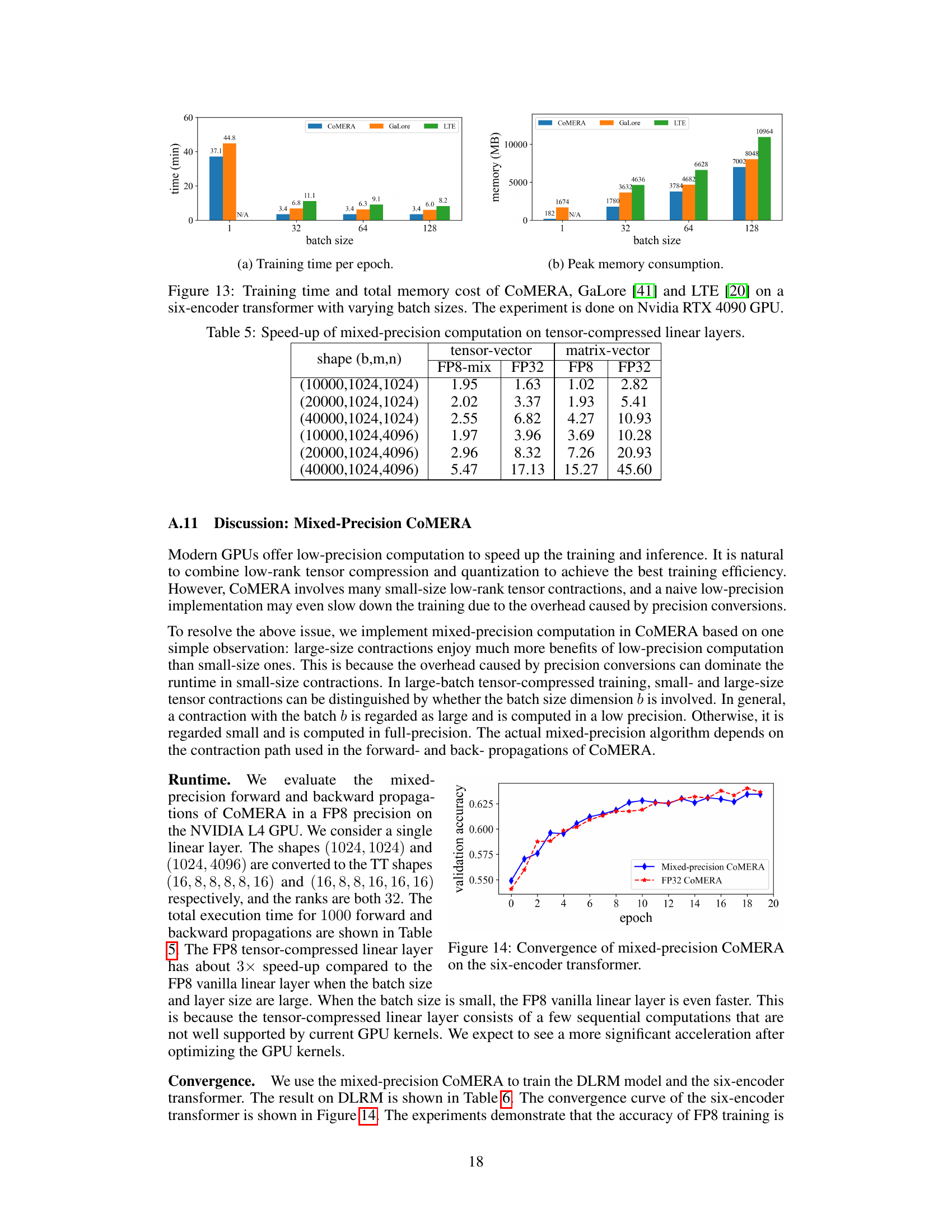
This figure compares the training time per epoch and peak memory consumption of three different training methods: COMERA, GaLore, and LTE. The comparison is made across various batch sizes (1, 32, 64, 128) using a six-encoder transformer model and an Nvidia RTX 3090 GPU. The results show that COMERA outperforms the other two methods in both training time and memory efficiency.
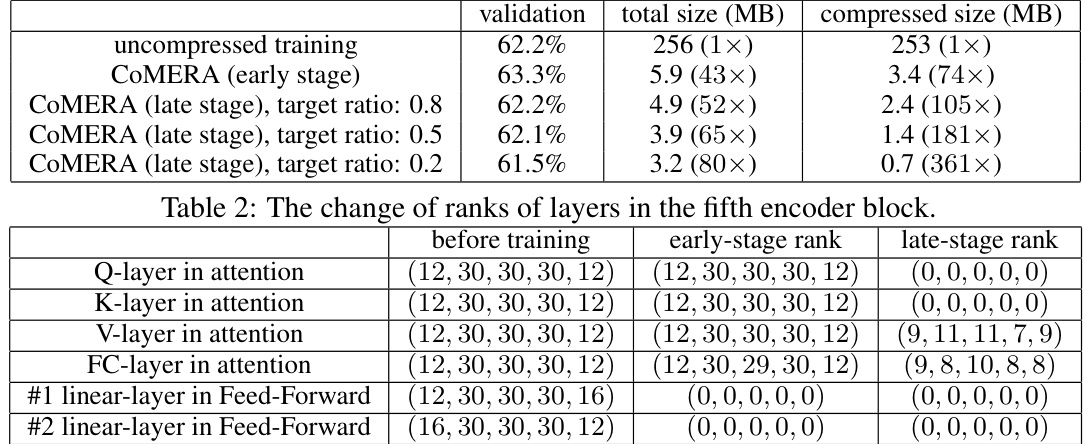
This table shows how the ranks of layers in the fifth encoder block change during the training process using CoMERA. It compares the ranks before training, after the early stage of training, and after the late stage of training. The late-stage training uses different target compression ratios (0.8, 0.5, and 0.2), resulting in varying degrees of rank reduction. Notice that some layers end up with all ranks at zero, indicating that these layers were effectively removed by the model during the rank-adaptive training process.
In-depth insights#
Rank-Adaptive Tuning#
Rank-adaptive tuning represents a significant advancement in efficient model training. By dynamically adjusting the rank of tensors during the training process, this technique offers a powerful means to balance model accuracy and computational cost. The core idea is to intelligently control the dimensionality of tensor representations according to the specific needs of the model, thereby enabling significant compression without sacrificing accuracy. Multi-objective optimization plays a crucial role, ensuring that rank adjustments are guided by a strategy that simultaneously minimizes both training loss and model size. This approach moves beyond traditional fixed-rank methods that often lead to suboptimal performance due to inflexibility. Careful GPU optimization techniques further enhance the efficiency, making rank-adaptive tuning a practically viable and efficient approach for training large-scale deep learning models. The method demonstrates potential for significant speedups, memory savings, and reduced environmental impact compared to traditional training methods. This is particularly crucial in the era of ever-larger language models and increasingly resource-intensive AI applications.
Multi-Objective Opt#
The heading “Multi-Objective Optimization” suggests a sophisticated approach to training large AI models. Instead of focusing solely on minimizing error (a single objective), this method likely simultaneously optimizes multiple, potentially competing goals. This could involve balancing model accuracy with factors like compression ratio, training time, and memory usage. The advantage is a more adaptable training process that can be tailored to specific resource constraints or hardware limitations. Finding the optimal balance between these objectives, represented as a Pareto point, is crucial. The resulting model would be more efficient, and possibly more deployable across various platforms or devices. Successfully implementing multi-objective optimization likely requires a novel mathematical formulation and potentially advanced algorithms to search the solution space effectively. Robustness and stability of the optimization process are key challenges, as a poorly designed multi-objective approach could lead to inferior performance compared to simpler, single-objective methods.
GPU Performance Boost#
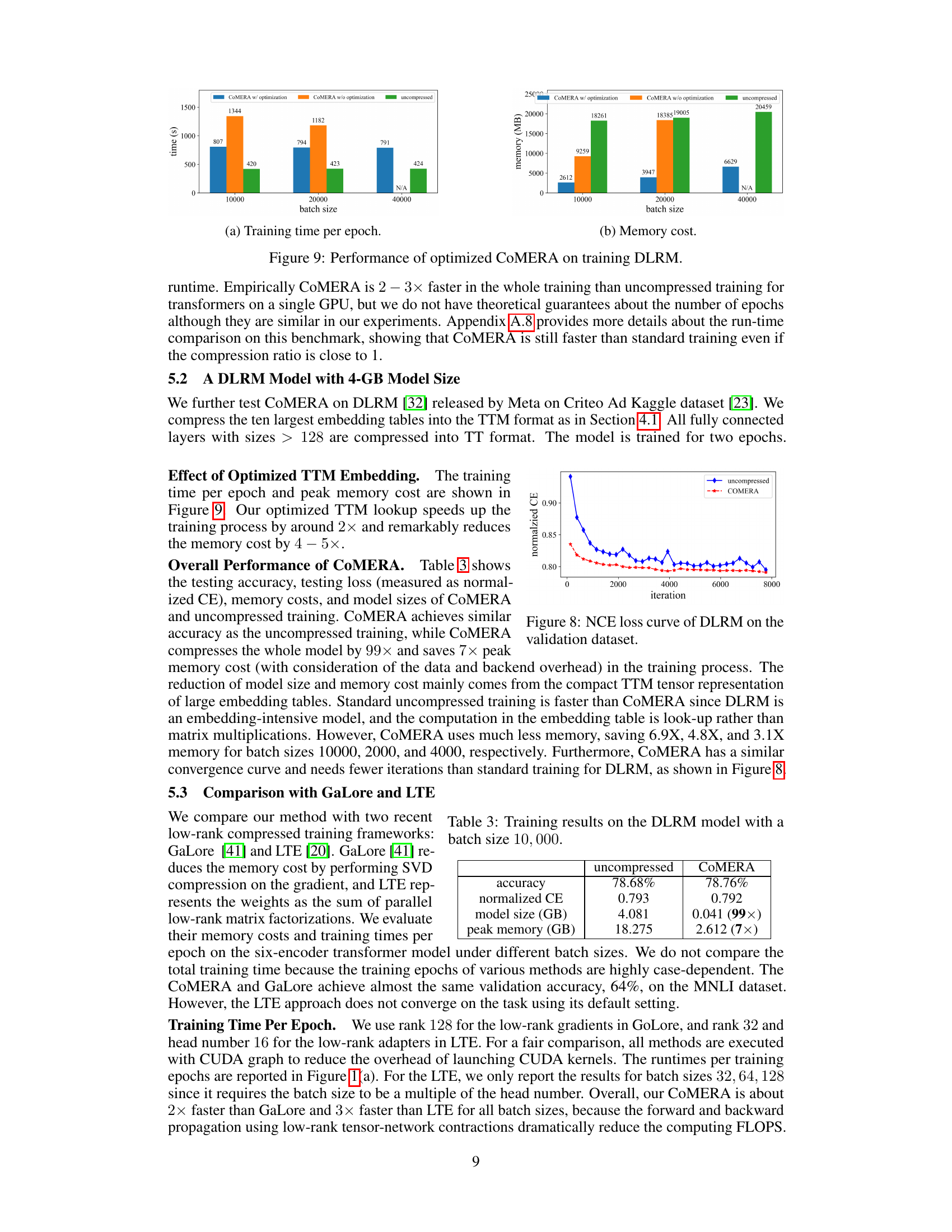
The research paper explores methods to accelerate GPU performance during the training of large AI models. A critical challenge is that low-rank tensor compression, while reducing memory and FLOPS, often slows down practical training due to the overhead of many small tensor operations on GPUs. To address this, the paper proposes three key optimizations. First, optimized TTM embedding table lookups significantly reduce redundancy in accessing embedding vectors. Second, contraction path optimization for TT-vector multiplications streamlines the computation of linear layers, reducing overhead. Lastly, CUDA Graph optimization helps to eliminate GPU backend overhead, leading to tangible speedups. These optimizations, when combined, demonstrate a notable improvement in training efficiency on GPU, achieving real-world speedups compared to standard training, a significant achievement given the usual trade-off between compression and speed.
LLM Pre-training Speedup#
The research explores accelerating Large Language Model (LLM) pre-training. A key finding is the substantial speedup achieved, reaching 1.9x to 2.3x faster pre-training compared to standard methods on a CodeBERT-like model. This improvement stems from a novel tensor-compressed training framework (CoMERA) which utilizes optimized numerical computations and GPU implementation. CoMERA’s multi-objective optimization strategically balances compression ratio and model accuracy, leading to efficient resource utilization. While impressive speed gains are reported, the study also acknowledges the need for further HPC (High-Performance Computing) optimization to fully realize CoMERA’s potential for drastically reducing pre-training costs across a broader range of LLMs. The results suggest a significant step towards making LLM development more accessible and environmentally friendly, especially considering the massive computational demands of current pre-training processes.
Future Work: HPC#
The paper’s ‘Future Work: HPC’ section strongly suggests that significant performance gains are achievable through high-performance computing (HPC) optimization. Currently, the CoMERA framework, while demonstrating speedups on a single GPU, hasn’t been fully optimized for distributed or parallel HPC environments. The authors acknowledge that the small-size tensor operations, beneficial for memory efficiency, are not currently well-optimized by existing GPU kernels. This indicates a potential bottleneck limiting scalability. Therefore, future work should focus on developing and integrating custom HPC kernels designed to efficiently handle the unique low-rank tensor computations used in CoMERA. This might involve exploiting specialized hardware or parallel processing strategies to overcome the performance limitations observed with standard GPU kernels on smaller tensor operations. Successfully addressing this would likely yield substantial improvements in training speed, making CoMERA even more competitive for large-scale AI model training. Furthermore, investigating other HPC-specific optimization techniques, such as advanced communication protocols or memory management strategies, would be crucial for maximizing performance in large-scale training scenarios.
More visual insights#
More on figures
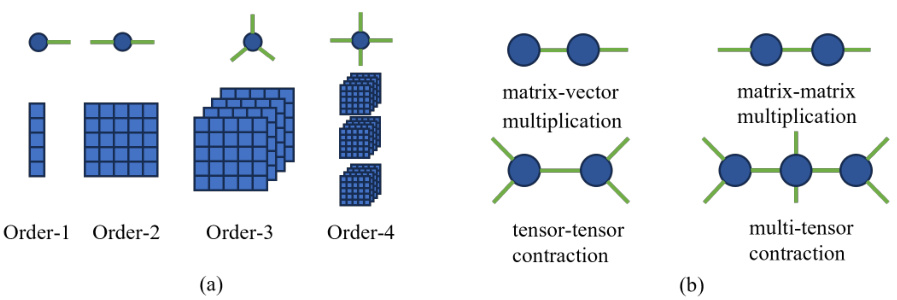
This figure visualizes tensors and tensor contractions. Part (a) shows the tensor network representations for tensors of orders 1, 2, 3, and 4. Part (b) illustrates several common tensor contractions: matrix-vector multiplication, matrix-matrix multiplication, tensor-tensor contraction, and multi-tensor contraction. These operations are fundamental to tensor networks, and visualizing them helps to understand the computational aspects discussed in the paper.
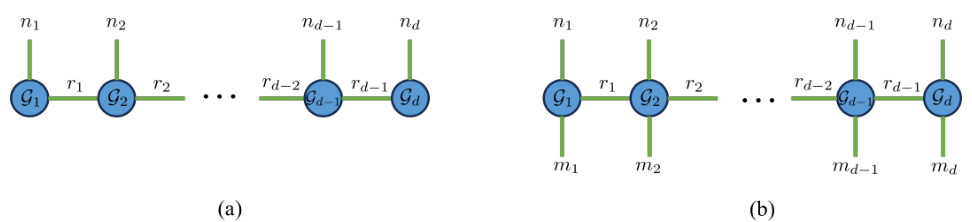
This figure illustrates the tensor network structures for tensor-train (TT) and tensor-train matrix (TTM) decompositions. The TT decomposition represents a tensor as a sequence of smaller, interconnected cores (G1, G2,…, Gd) connected in a chain-like fashion, where the dimensions of each core are determined by the ranks (r0, r1,…, rd) and the original tensor’s dimensions (n1, n2,…, nd). The TTM decomposition extends this concept, handling unbalanced dimensions more effectively. It represents the tensor as a similar chain, but each core (F1, F2,…, Fd) incorporates both the dimensions from the TT decomposition (ni) and additional dimensions (mi). The figure visually depicts these connections between the cores and how they combine to form the original tensor.
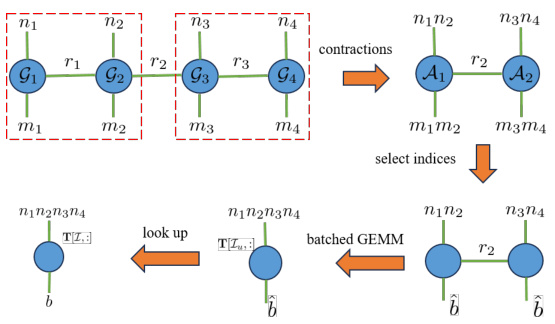
This figure illustrates the optimized process of looking up entries in a tensor-train matrix (TTM) embedding table. It demonstrates how the process efficiently selects submatrices from the compressed TTM representation to avoid redundant computations. This optimization significantly reduces both memory consumption and computational cost, as detailed in Section 4.1 of the paper. The figure shows the steps involved: reshaping the embedding table into a tensor, selecting indices, performing tensor contractions, and finally, employing batched GEMM (generalized matrix multiplication) to obtain the desired results.

This figure compares the performance of five different methods for optimizing TTM embedding table lookups. The ‘uncompressed’ method represents the standard approach without any optimization. The ‘proposed approach’ is the new method introduced in section 4.1 of the paper, which aims to accelerate the lookup process by eliminating redundant computations. The ‘optimized order’, ‘unique indices’, and ‘without optimization’ methods represent variations of the proposed approach with different levels of optimization applied. The graph displays the speedup (left) and memory reduction (right) achieved by each method for different batch sizes (10000, 20000, 40000).
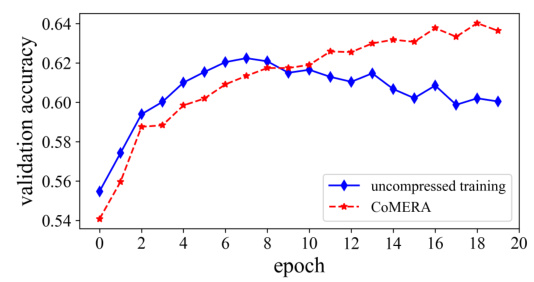
This figure shows the validation accuracy during the early-stage training of CoMERA on the MNLI dataset. It illustrates the training progress and how the model’s performance on a validation set changes over epochs. The graph indicates that CoMERA achieves comparable validation accuracy to the uncompressed training approach while significantly reducing model size and training time.
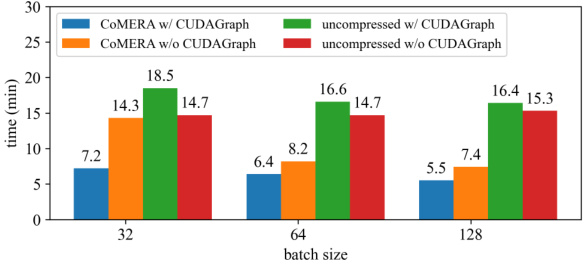
This figure compares the training time per epoch for different methods on the MNLI dataset using a six-encoder transformer model. The methods compared are CoMERA with and without CUDA Graph, and uncompressed training with and without CUDA Graph. The x-axis represents the batch size used (32, 64, and 128), and the y-axis shows the training time in minutes. The figure demonstrates the significant speedup achieved by CoMERA, especially when utilizing CUDA Graph for optimization.
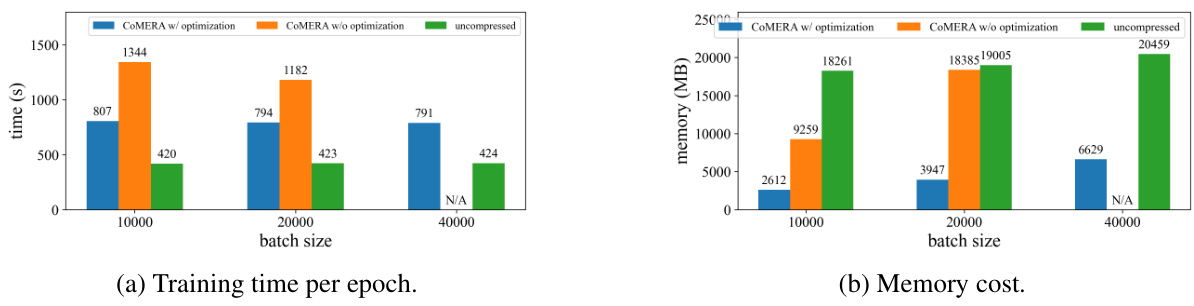
This figure compares the training time per epoch and memory cost of three different methods: COMERA with optimization, COMERA without optimization, and uncompressed training. The comparison is shown for three different batch sizes (10000, 20000, 40000). The results demonstrate that COMERA, especially with optimizations, significantly reduces both training time and memory consumption compared to uncompressed training, especially at larger batch sizes. The lack of a value for 40000 batches in the uncompressed scenario suggests that training at that scale may have been infeasible without optimization.
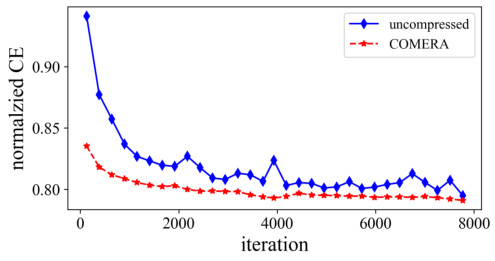
This figure shows the training loss curve for both the uncompressed and COMERA methods on the DLRM model during the validation phase. The x-axis represents the training iteration, and the y-axis represents the normalized cross-entropy (NCE) loss. The plot visually demonstrates the convergence of both methods, with COMERA showing a slightly higher loss at the end of training.

This figure shows the pre-training loss curves for both the original CodeBERT model and the CoMERA-compressed version. The x-axis represents the training steps, and the y-axis represents the training loss. The figure is divided into two phases. In Phase 1, both models show a similar downward trend in loss. In Phase 2, a further compression step is introduced in CoMERA, leading to a slight increase in loss initially before it continues its downward trend. The main observation is that CoMERA achieves comparable performance to CodeBERT despite significant model compression.
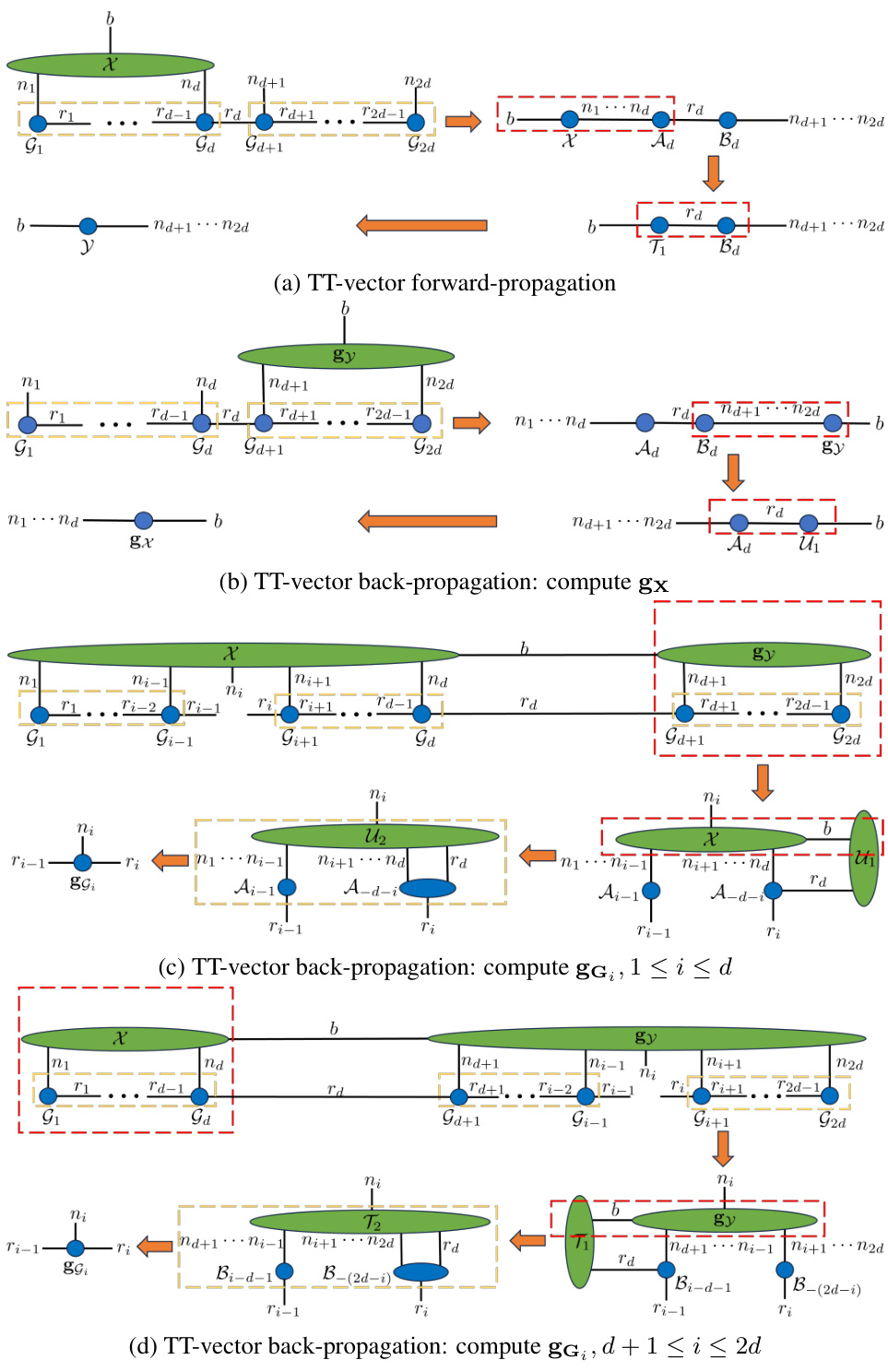
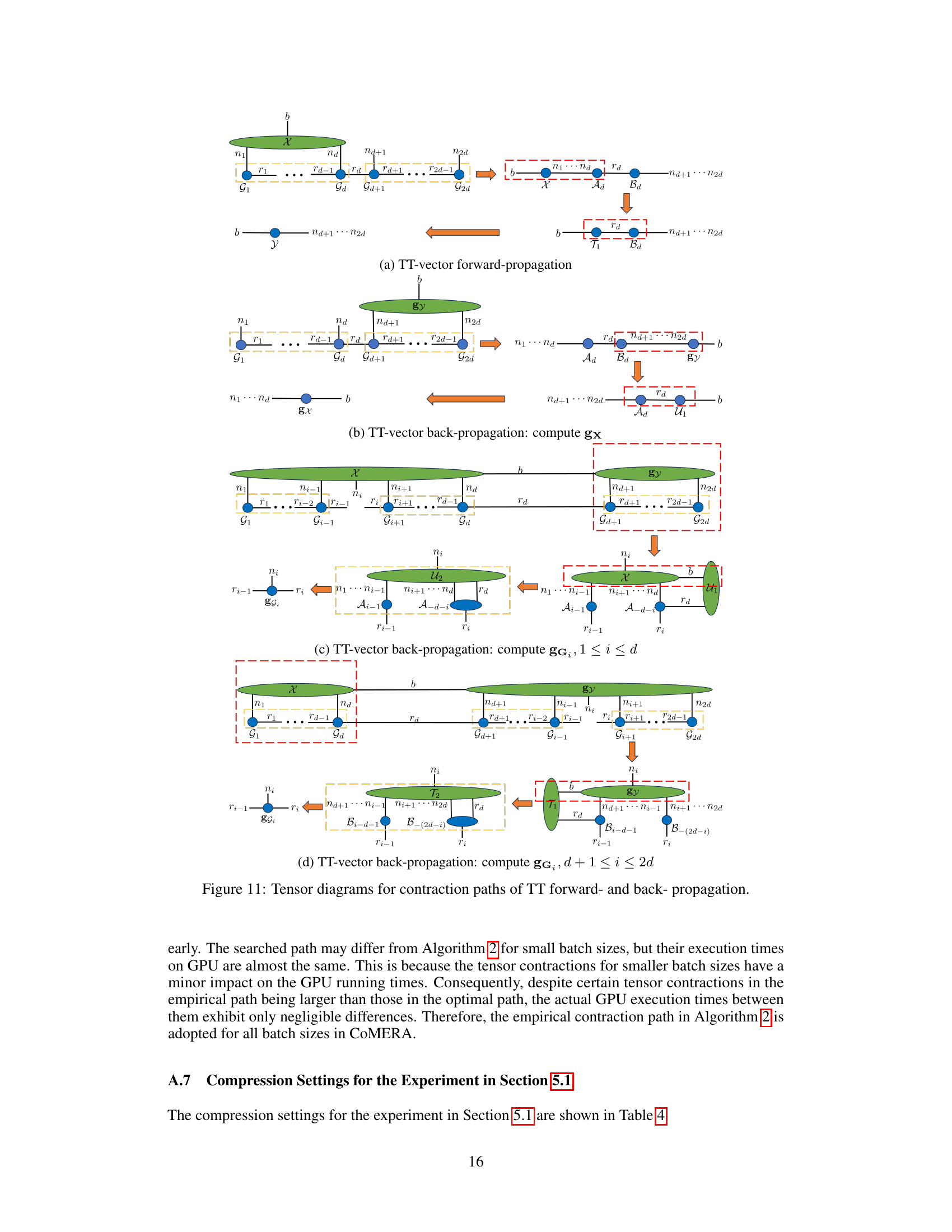
This figure shows the tensor diagrams for the contraction paths used in the forward and backward propagation of TT-vector multiplications. The diagrams illustrate the computational flow for both forward and backward passes, broken down into smaller, manageable steps. This visualization aids in understanding how the algorithm optimizes the order of tensor contractions to minimize computational cost and memory usage. The diagrams show different paths for computing gradients of the TT cores in the forward and backward passes.
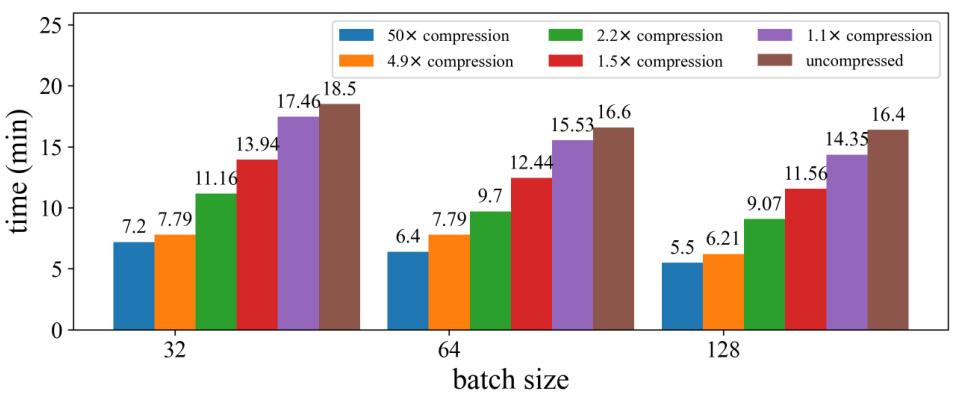
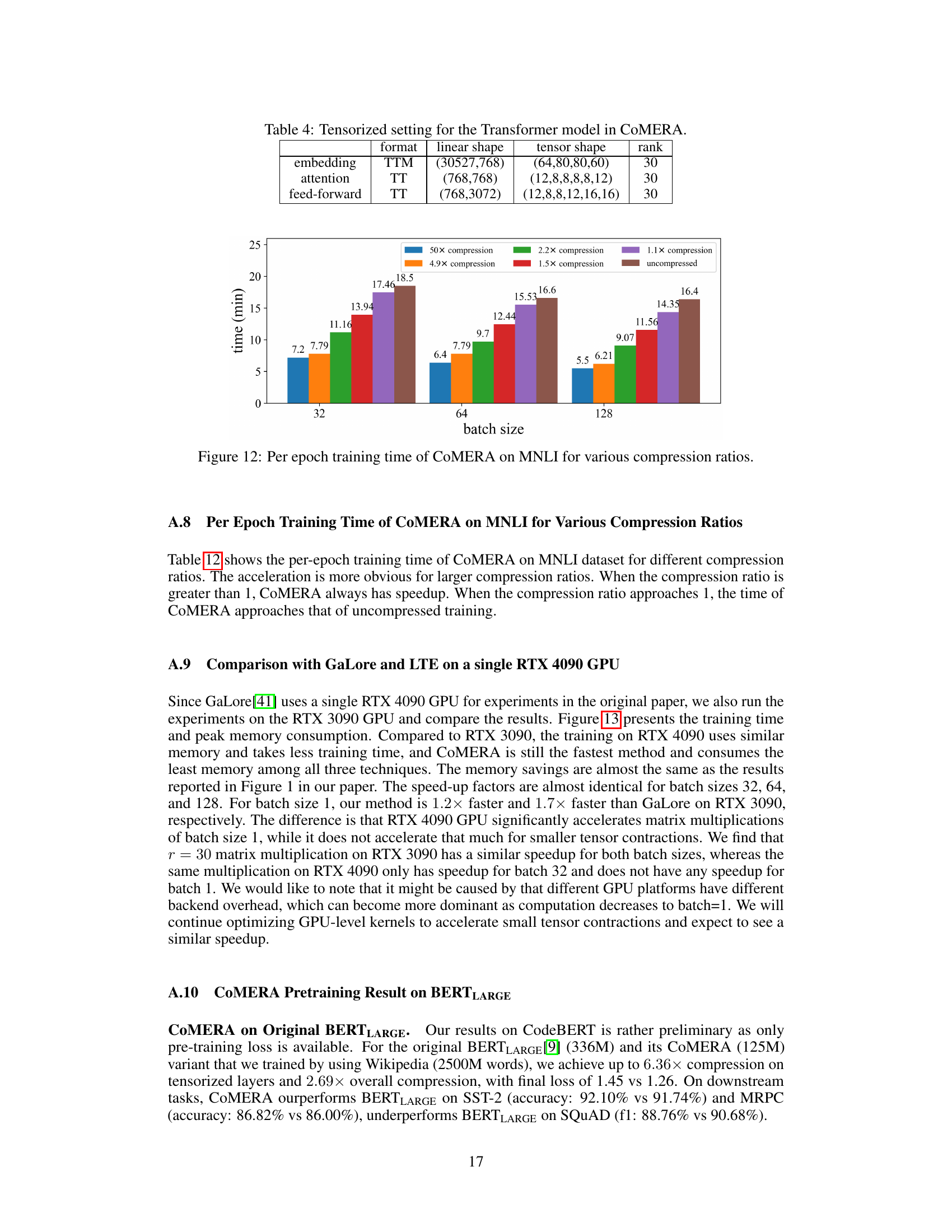
This figure shows the training time per epoch for the six-encoder transformer model on the MNLI dataset with different compression ratios. It demonstrates that CoMERA achieves significant speed-up in training time compared with standard training, especially for high compression ratios. The speedup is more obvious for larger compression ratios, approaching uncompressed training time as the compression ratio approaches 1.

This figure compares the training time per epoch and peak memory consumption of three different training methods: COMERA, GaLore, and LTE. The comparison is done on a six-encoder transformer model using different batch sizes (1, 32, 64, 128) and running on an Nvidia RTX 3090 GPU. The results show that COMERA significantly outperforms GaLore and LTE in terms of both training speed and memory efficiency.
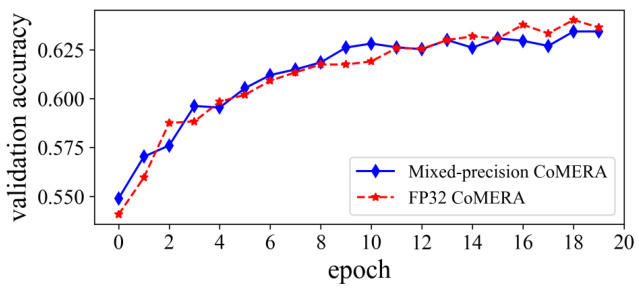
This figure shows the validation accuracy over training epochs for both mixed-precision and FP32 versions of CoMERA on a six-encoder transformer model. It demonstrates the comparable convergence speed and accuracy of the mixed-precision approach compared to the standard FP32 training.
More on tables
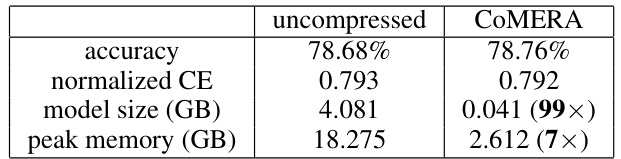
This table presents a comparison of the training results for the Deep Learning Recommendation Model (DLRM) using both uncompressed and CoMERA methods. It shows the accuracy, normalized cross-entropy (CE) loss, model size, and peak memory usage for each method. The results demonstrate that CoMERA achieves similar accuracy with a significantly smaller model size and lower peak memory consumption compared to the uncompressed method.

This table presents the results of training a transformer model on the MNLI dataset using different methods: uncompressed training and CoMERA with varying target compression ratios (0.8, 0.5, 0.2). For each method, it shows the validation accuracy, the total model size (in MB), and the compressed size of the tensorized layers (in MB). The table demonstrates the effectiveness of CoMERA in compressing the model while maintaining high accuracy.

This table shows the tensorization settings used for different layers in the Transformer model within the COMERA framework. It specifies the format (TTM or TT) employed for compressing the weight matrices, the original linear shape of the weight matrices, the reshaped tensor shape after applying the chosen tensor decomposition, and the rank (a hyperparameter affecting the compression level) used for each layer type.

This table presents the speedup achieved by using mixed-precision computation (FP8-mix) compared to using full precision (FP32) for both tensor-vector and matrix-vector multiplication in CoMERA. Different input tensor shapes (b, m, n) are tested, where b represents the batch size, m is the input dimension, and n is the output dimension. The speedup is calculated as the ratio of the execution time of FP32 to the execution time of the respective mixed-precision method. The table shows that significant speedups can be obtained by utilizing mixed-precision computation, especially for larger tensor shapes.

This table presents the training results of the DLRM model using two different precision methods: FP32 CoMERA (full precision) and FP8/FP32 mixed-precision CoMERA. The results show the accuracy and normalized cross-entropy (CE) loss achieved by each method. The data is for a batch size of 10,000.
Full paper#