↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Offline reinforcement learning struggles with the ‘out-of-distribution’ problem, especially when training data comes from multiple behavior policies with varying data quality. This leads to a ‘constraint conflict’ where inconsistent actions and returns across the state space hinder effective learning. Existing methods often try to prioritize ‘high-advantage’ samples, but this ignores the diversity of behavior policies.
This paper introduces Advantage-Aware Policy Optimization (A2PO) to solve this problem. A2PO uses a conditional variational autoencoder (CVAE) to disentangle the action distributions of different behavior policies, modeling the advantage values as conditional variables. Then, it trains an agent policy that optimizes for high-advantage actions while adhering to the disentangled constraints. Experiments show A2PO outperforms existing methods on various benchmark datasets, demonstrating its effectiveness in handling the challenges of mixed-quality data.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in offline reinforcement learning because it directly addresses the prevalent constraint conflict issue in mixed-quality datasets. Its novel A2PO method significantly improves performance compared to existing approaches by disentangling behavior policies using a conditional variational autoencoder and optimizing advantage-aware policy constraints. This offers a new perspective for handling the challenges of diverse data quality, thus opening avenues for more robust and effective offline RL algorithms.
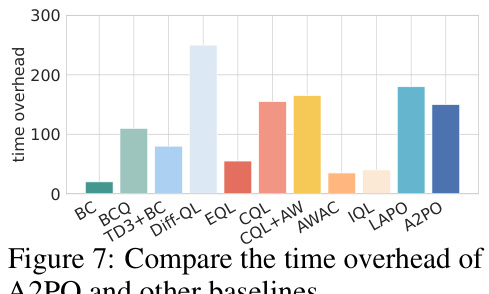
Visual Insights#
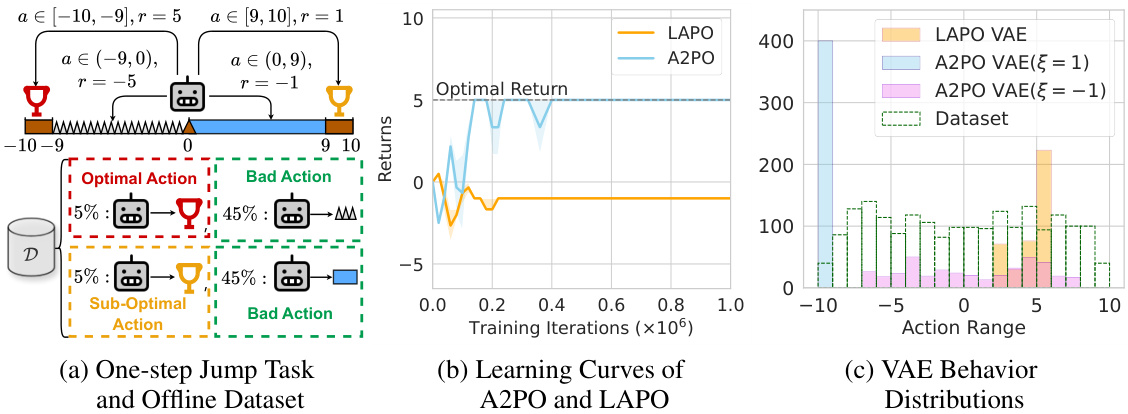
This figure presents a didactic experiment to illustrate the advantage of the proposed A2PO method over LAPO. (a) shows a simple one-step jump task with a mixed-quality dataset containing optimal, sub-optimal, and bad actions with different reward values. (b) compares the learning curves of A2PO and LAPO, demonstrating A2PO’s superior performance. (c) visualizes the VAE-generated action distributions for both methods, highlighting that A2PO’s VAE considers both state and advantage, unlike LAPO’s state-only approach.
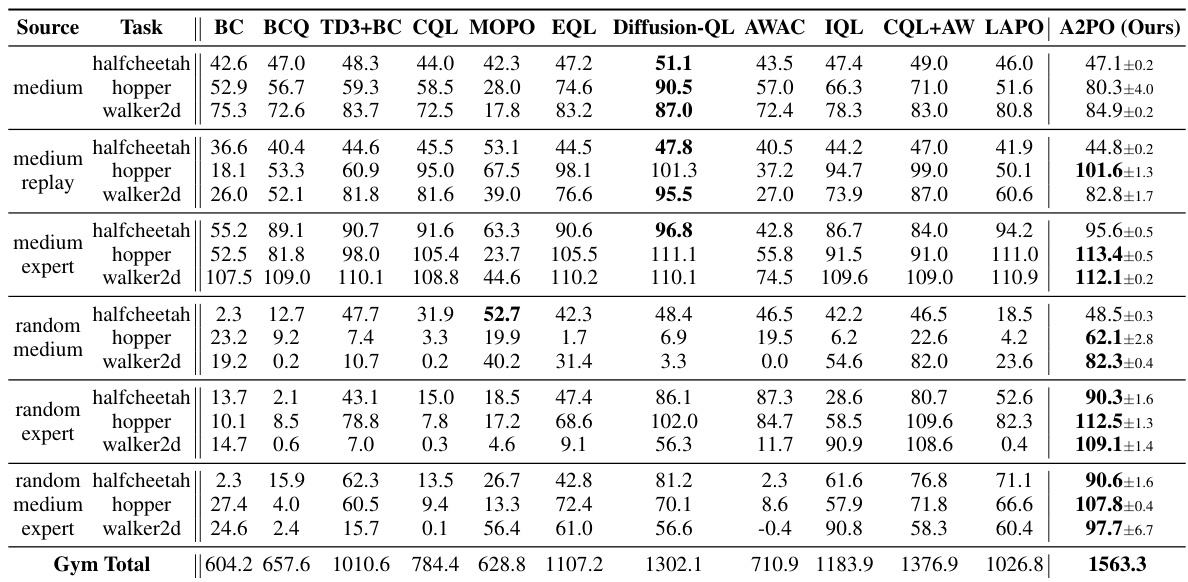
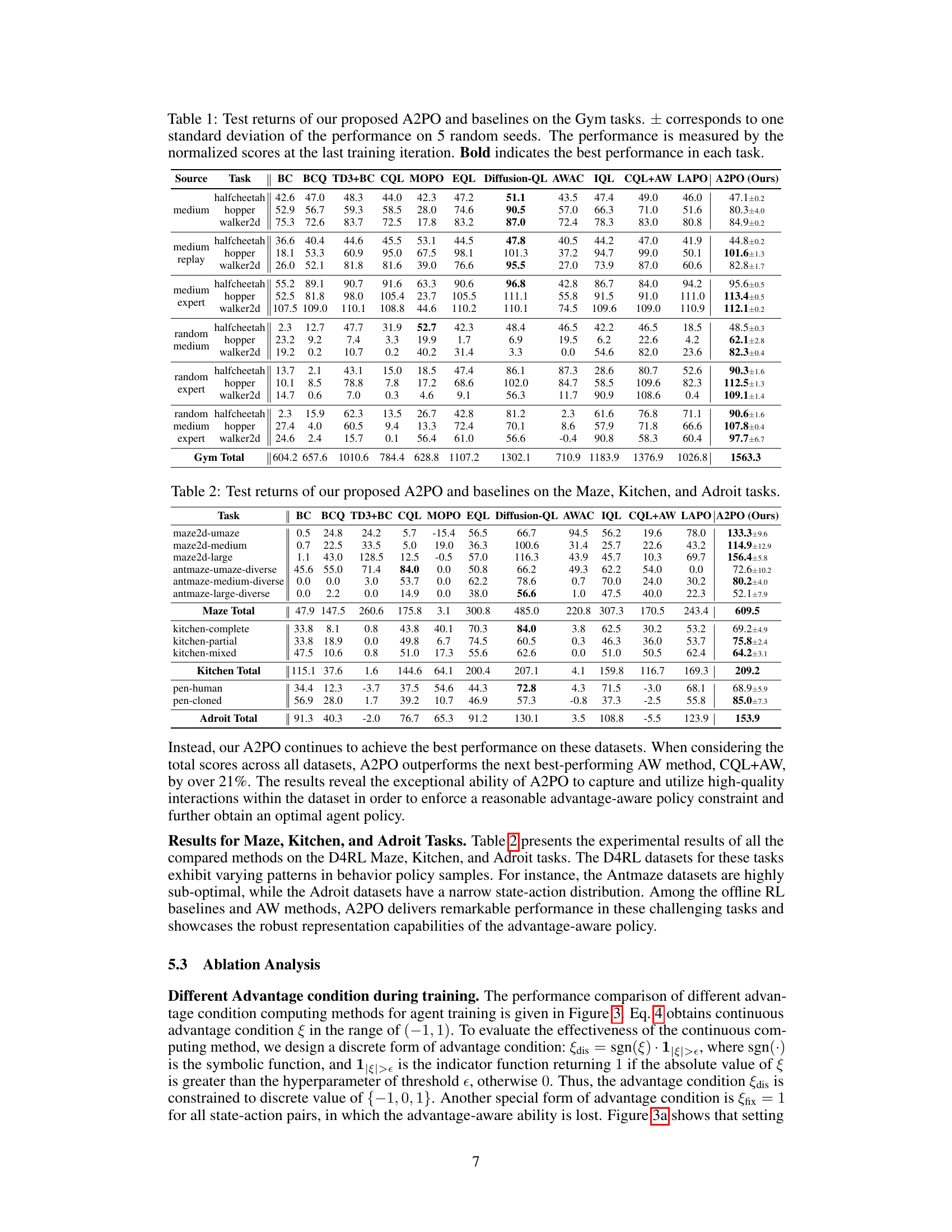
This table presents the test returns achieved by the proposed A2PO method and several baseline algorithms across various Gym tasks in the D4RL benchmark. The results represent the average normalized scores at the final training iteration, with ± indicating the standard deviation across five different random seeds. The bolded values highlight the best-performing algorithm for each task.
In-depth insights#
Offline RL OOD#
Offline reinforcement learning (RL) tackles the challenge of training agents using only pre-collected data, eliminating the need for online interaction. A critical issue in offline RL is the out-of-distribution (OOD) problem, where the learned policy encounters situations unseen during data collection. This leads to poor performance because the agent extrapolates beyond the learned data distribution. Addressing the OOD problem requires careful consideration of how to constrain the policy’s behavior, ensuring it remains within the bounds of the observed data. Common approaches include policy constraint methods, which directly restrict the policy’s deviation from the behavior policy, and value regularization techniques, which aim to prevent overestimation of rewards in unseen states. However, these methods can be overly conservative, limiting performance. Advantage-weighted approaches offer a potential solution by prioritizing samples with high advantage values, focusing training on areas where the potential for improvement is greatest. The effectiveness of each method depends significantly on the characteristics of the offline dataset and the specific RL task. Future research should focus on developing more sophisticated methods to better address OOD issues while maintaining performance, possibly through the combination of different approaches.
A2PO Framework#
The A2PO framework tackles the challenge of offline reinforcement learning with mixed-quality datasets by disentangling behavior policies and incorporating advantage-aware constraints. A key innovation is the use of a conditional variational autoencoder (CVAE) to model action distributions conditioned on advantage values. This allows A2PO to effectively separate actions from different behavior policies, preventing conflicts arising from inconsistent returns across the state space. The framework then optimizes an agent policy that prioritizes high-advantage actions while adhering to the disentangled behavior policy constraints. This two-stage process (disentangling and optimization) is crucial for effective learning from diverse, potentially low-quality data. Furthermore, A2PO’s design explicitly addresses the constraint conflict problem, which is a significant limitation of previous advantage-weighted methods. By directly modelling the advantage, A2PO avoids implicit data redistribution that can negatively impact data diversity. The results demonstrate significant performance gains, particularly on mixed-quality datasets, showcasing the framework’s effectiveness in complex and challenging offline RL scenarios.
Advantage Disentanglement#
Advantage disentanglement in offline reinforcement learning addresses the challenge of inconsistent data from multiple behavior policies. Existing methods often struggle with conflicting constraints arising from varying data quality, where samples with high advantage values are prioritized, potentially neglecting valuable data from less effective policies. A key insight is that disentangling the underlying action distributions of these policies is crucial. By separating the influences of different behavior policies, the algorithm can better learn a consistent and effective policy, reducing the risk of extrapolation error from out-of-distribution samples. Techniques like conditional variational autoencoders (CVAEs) can be used to model the data’s advantage and disentangle behavior policies. This allows the agent to learn a policy that considers the relative value of actions across different data sources, leading to improved performance, particularly in mixed-quality offline datasets. The effectiveness hinges on the ability of the CVAEs to correctly model the conditional distributions, accurately isolating the influence of individual behavior policies on action selection.
Empirical Evaluation#
An Empirical Evaluation section in a research paper would typically present results obtained from experiments designed to validate the paper’s claims. A strong section would clearly state the experimental setup, including datasets used, metrics employed, and the baselines against which the proposed method is compared. Detailed descriptions of the experimental design are vital for reproducibility. The results should be presented clearly, often using tables and figures to compare performance across various conditions. Crucially, statistical significance testing should be conducted and reported, to ensure that observed differences are not due to random chance. Finally, a thoughtful discussion of the results is essential. This discussion should highlight the key findings, relate them back to the paper’s hypotheses, acknowledge any limitations of the experiments, and suggest potential future work based on the observations.
Future Work#
The paper’s “Future Work” section could explore several promising avenues. Extending A2PO to multi-task offline RL is crucial, as real-world scenarios often involve diverse tasks and policies. Addressing the limitations of the CVAE’s computational cost and exploring more efficient alternatives could improve scalability. A deeper investigation into the impact of different advantage function designs would reveal whether alternative methods enhance performance. Further exploration into the robustness of A2PO on datasets with highly diverse behavior policies and noisy data is important to establish practical applicability. Finally, theoretical analysis to formally prove the convergence and sample efficiency of A2PO is a significant area for future research.
More visual insights#
More on figures
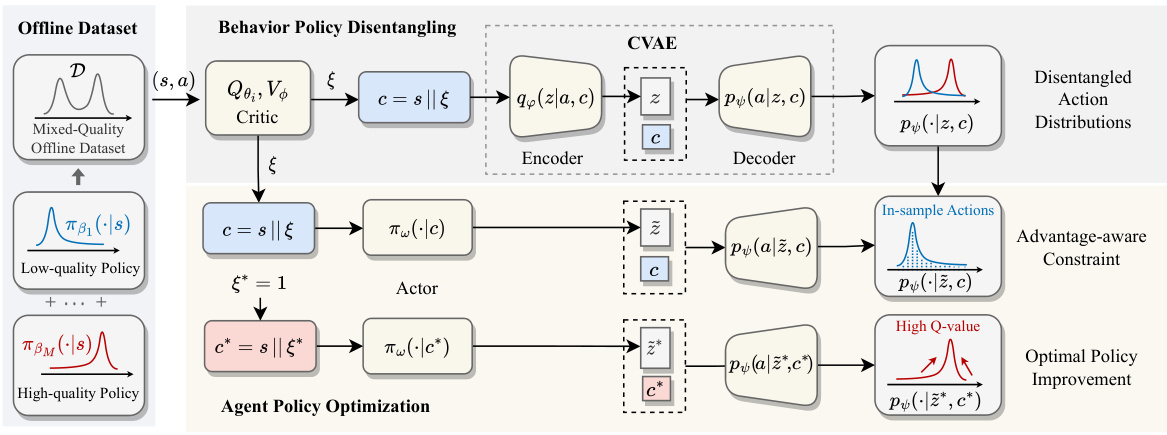
This figure shows a flowchart of the A2PO method. The process starts with an offline dataset of mixed quality. This dataset is fed into a Conditional Variational Autoencoder (CVAE) which disentangles the behavior policies. The CVAE’s output is conditioned on the advantage, a measure of how good an action is. Then this information is used in the agent policy optimization stage to create an advantage-aware policy which avoids out-of-distribution issues. This is achieved by utilizing the disentangled action distributions as a constraint on the agent’s policy during optimization. The actor network is updated using advantage values derived from two Q networks and a V network. The process results in an optimal policy.
This figure shows a didactic experiment using a simple one-step jump task to illustrate the differences between A2PO and LAPO. Panel (a) visualizes the task and the structure of the mixed-quality dataset, highlighting different reward values for different actions. Panel (b) presents learning curves, comparing the performance of A2PO and LAPO. Panel (c) visualizes the action distributions generated by the VAE components of each method, highlighting how A2PO conditions on both state and advantage, while LAPO only conditions on the state. This example demonstrates A2PO’s ability to prioritize samples with high advantage values while considering behavior policy diversity.
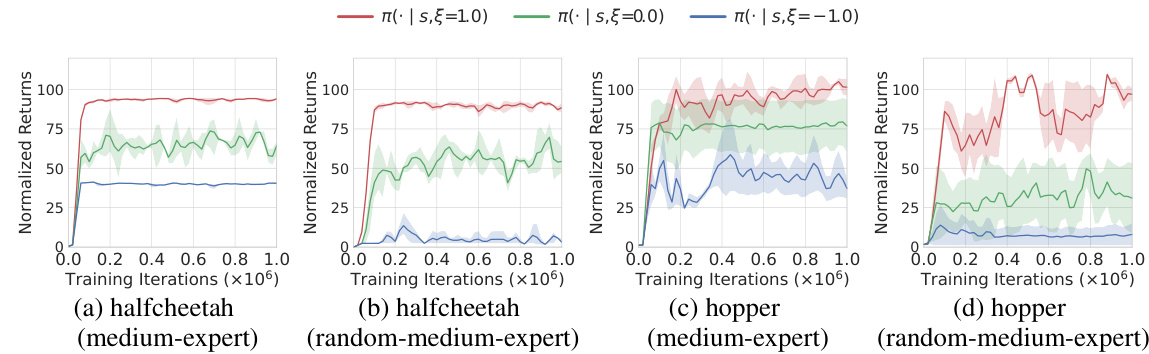
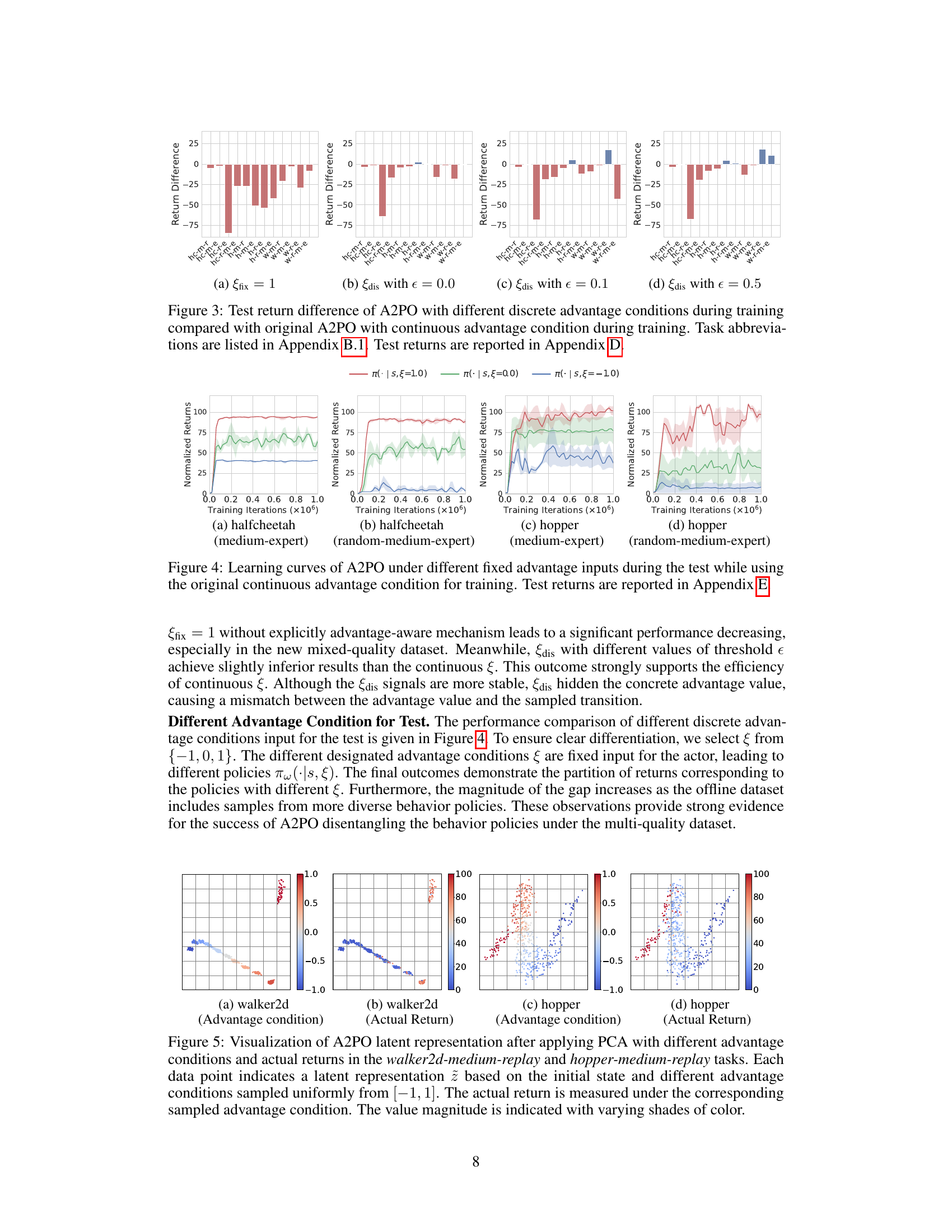
This figure displays the learning curves for A2PO across four different scenarios. Each scenario involves a specific task (halfcheetah or hopper) and dataset type (medium-expert or random-medium-expert). The key aspect shown is how the agent’s performance changes when it’s given different fixed advantage inputs (-1.0, 0.0, and 1.0) during testing. The curves reveal the impact of this advantage input on the learning process and final performance. Appendix E provides more detailed test return results.
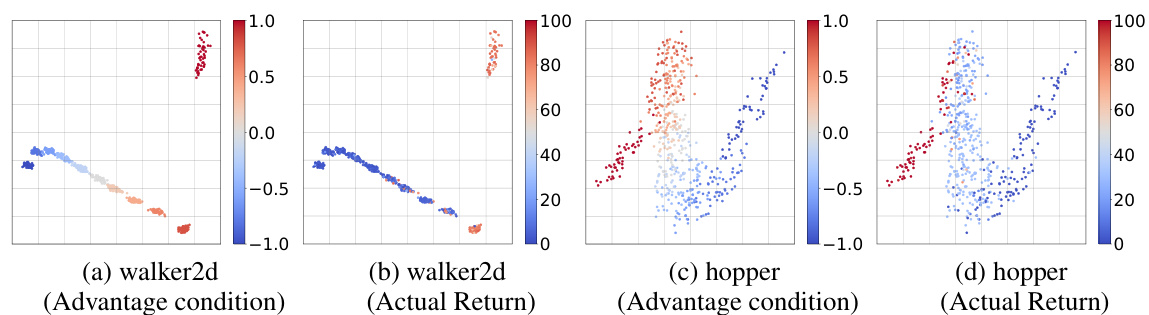
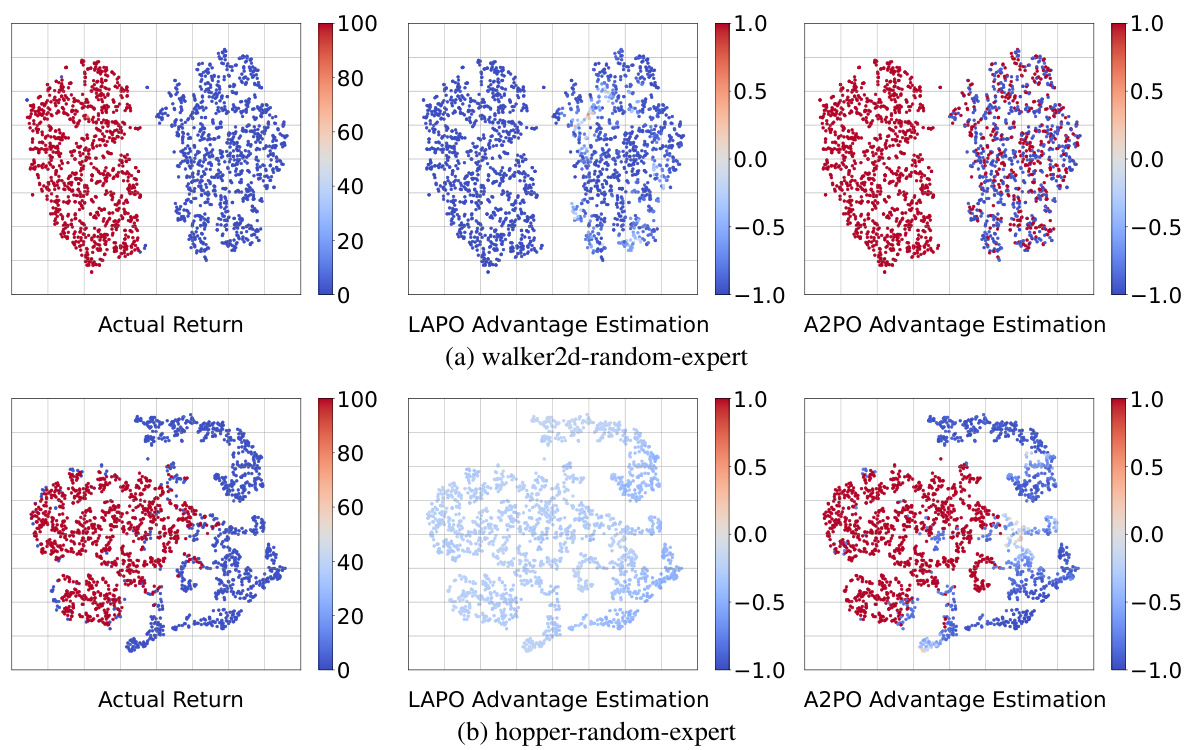
This figure compares the advantage estimation of A2PO and LAPO on random-expert mixed-quality datasets for the walker2d and hopper tasks in the Gym environment. It visualizes the initial state-action pairs using PCA, with color intensity representing the magnitude of the actual return and the advantage estimations from each method. The visualization helps to understand how well each method captures the relationship between actions, states, and their resulting returns, specifically highlighting the differences between A2PO and LAPO in advantage estimation on these more complex datasets.
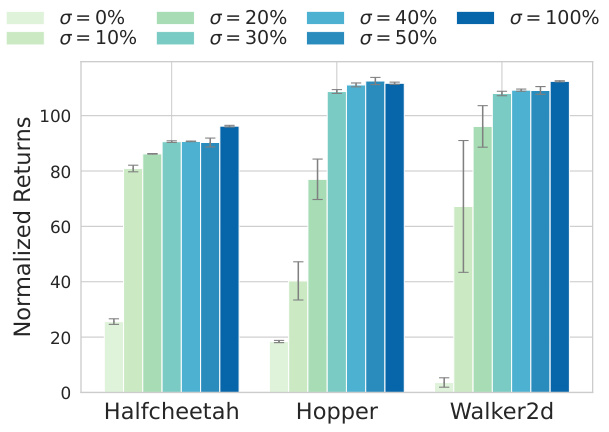
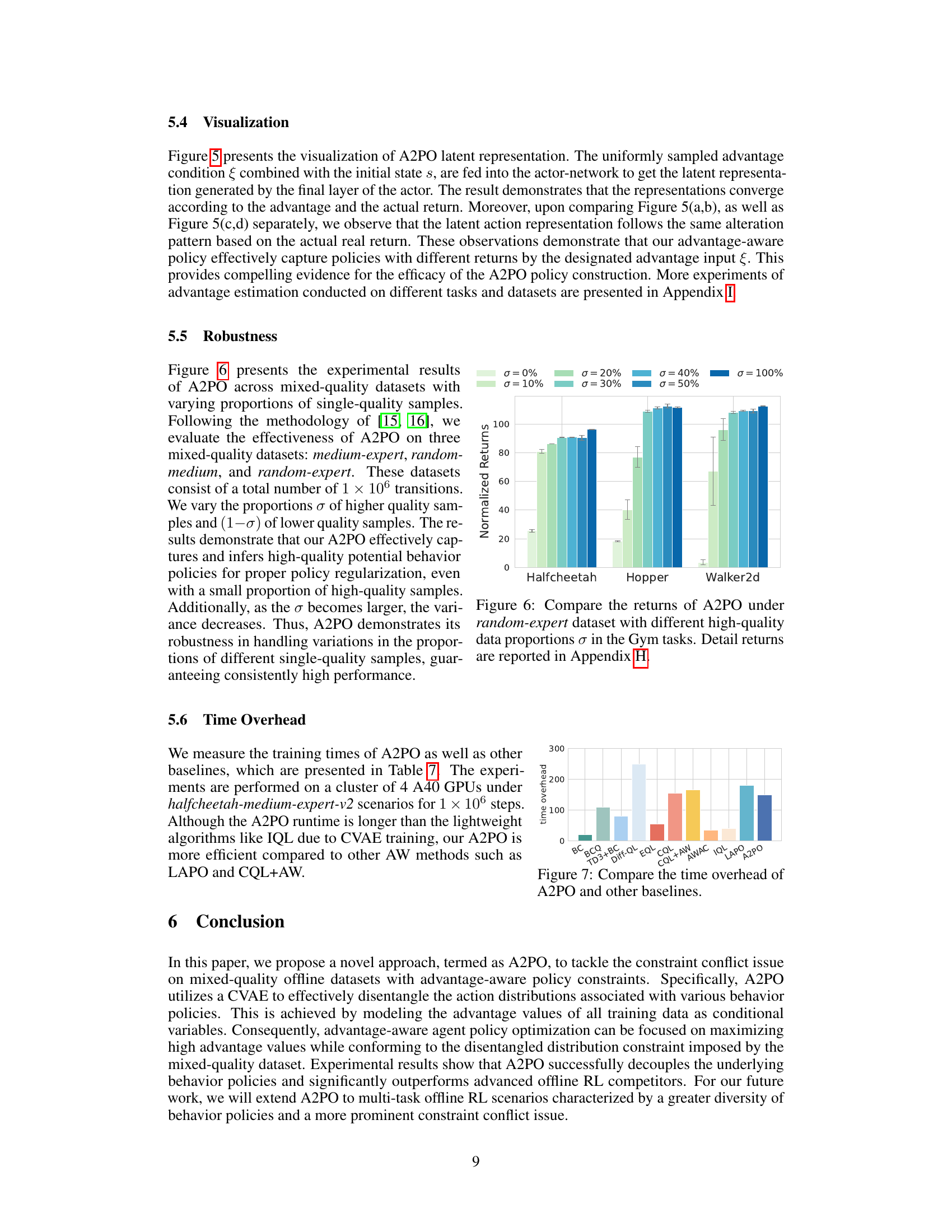
This figure shows the robustness of the A2PO algorithm in handling variations in the proportions of different single-quality samples. The results demonstrate that the A2PO method effectively captures and infers high-quality potential behavior policies, even with a small proportion of high-quality samples. The performance is consistently high across different proportions, demonstrating robustness.
This figure shows a didactic experiment using a toy one-step jump task to illustrate the difference between A2PO and LAPO. Panel (a) visualizes the task and the composition of the mixed-quality dataset. Panel (b) compares the learning curves of A2PO and LAPO, demonstrating A2PO’s superior performance. Panel (c) displays the VAE-generated action distributions, highlighting how A2PO conditions on both state and advantage, unlike LAPO which only conditions on state.
This figure shows a didactic experiment to illustrate the difference between A2PO and LAPO methods. Panel (a) visualizes a simple ‘one-step jump’ task and the structure of a mixed-quality dataset for this task. Panel (b) presents learning curves, showing A2PO’s superior performance compared to LAPO. Finally, panel (c) displays the action distributions generated by the VAE in both methods, highlighting the fact that A2PO conditions on both state and advantage while LAPO only conditions on the state.
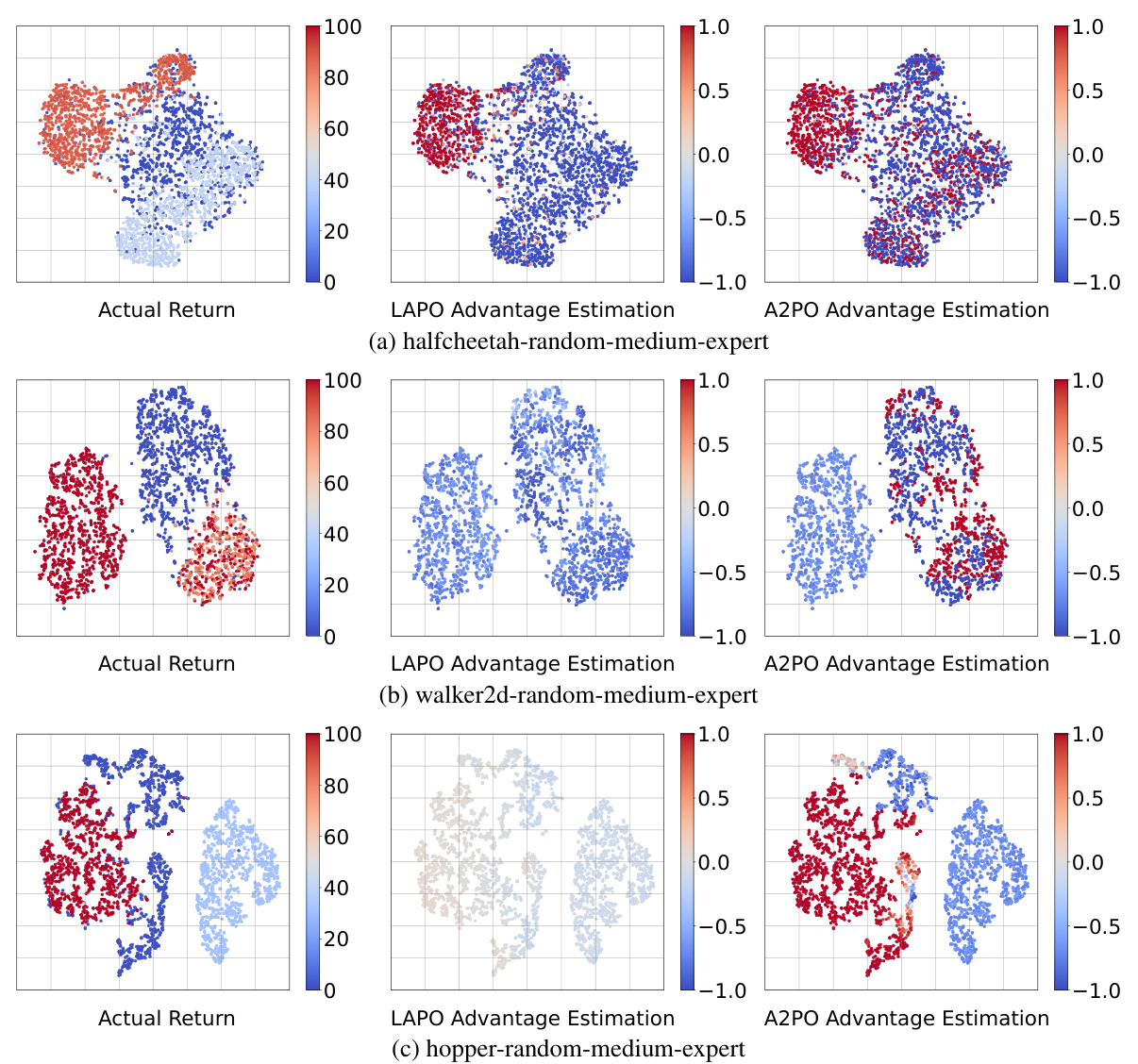
This figure compares the advantage estimation capabilities of A2PO and LAPO on mixed-quality datasets (random-medium-expert) from the D4RL benchmark for three locomotion tasks: halfcheetah, walker2d, and hopper. Using PCA, the initial state-action pairs are visualized. The color intensity represents the magnitude of the actual return or estimated advantage, allowing for a visual comparison of how well each method captures the advantage in different regions of the state-action space.
More on tables
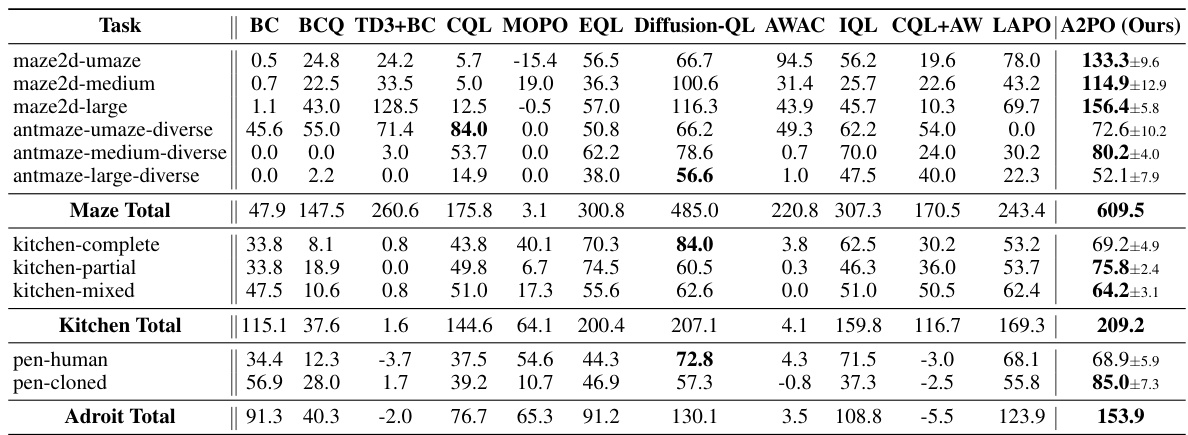
This table presents the experimental results of the proposed A2PO algorithm and various baseline methods on the D4RL Gym tasks. It shows the average test return (with standard deviation) achieved by each method across five random seeds. The best performing method for each task is highlighted in bold. The results are normalized scores from the final training iteration, illustrating the performance of each algorithm after training completion.

This table presents the test returns achieved by the proposed A2PO method and several baseline methods on various Gym tasks within the D4RL benchmark. The results are based on five random seeds, and the ± values represent one standard deviation of the performance across those seeds. The performance is evaluated using the normalized score from the last training iteration. The best performance for each task is highlighted in bold.
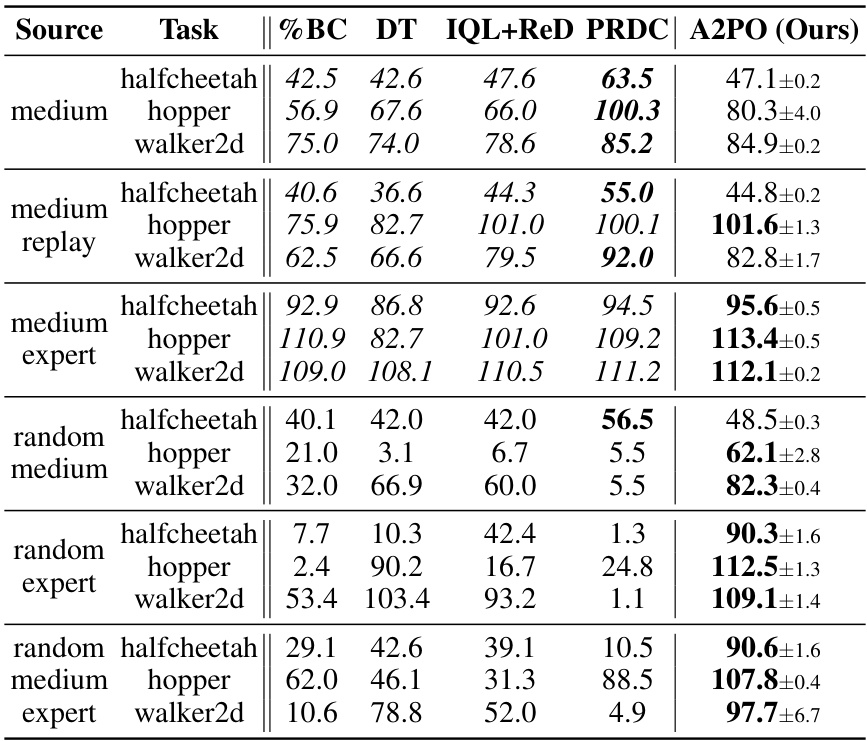
This table presents the test returns achieved by the proposed A2PO method and several baseline algorithms across different Gym tasks within the D4RL benchmark. The results are averaged across five random seeds, with ± representing the standard deviation. The performance metric is the normalized score obtained at the final training iteration. The best performing algorithm for each task is shown in bold.
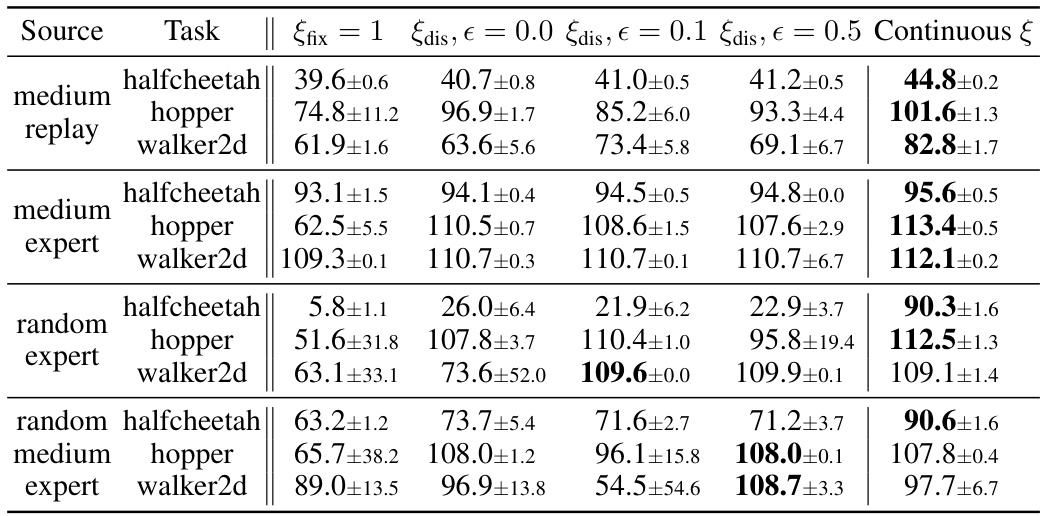
This table presents the test returns of the proposed A2PO method and several baseline algorithms on four different Gym tasks from the D4RL benchmark. The results are averaged over five random seeds, and the ± values represent the standard deviation. The performance metric is the normalized score at the final training iteration. The best performance for each task is highlighted in bold.
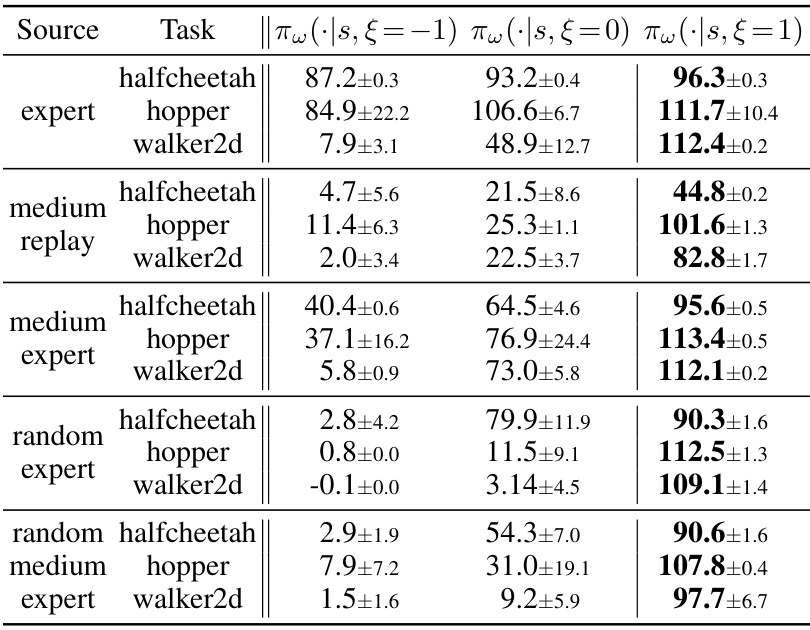
This table presents the test returns of the proposed A2PO algorithm and several baseline algorithms on various Gym tasks from the D4RL benchmark. The results are averaged over 5 random seeds, and the ± values represent one standard deviation. The performance metric used is the normalized score obtained at the final training iteration. Bold numbers highlight the best performance for each task.

This table compares the performance of two policies: the CVAE policy and the agent policy, across various tasks and datasets. The CVAE policy uses a Conditional Variational Auto-Encoder (CVAE) to generate actions, while the agent policy is learned by the Advantage-Aware Policy Optimization (A2PO) algorithm. The results show that the A2PO agent policy generally outperforms the CVAE policy, demonstrating the effectiveness of the A2PO algorithm in learning effective control policies.
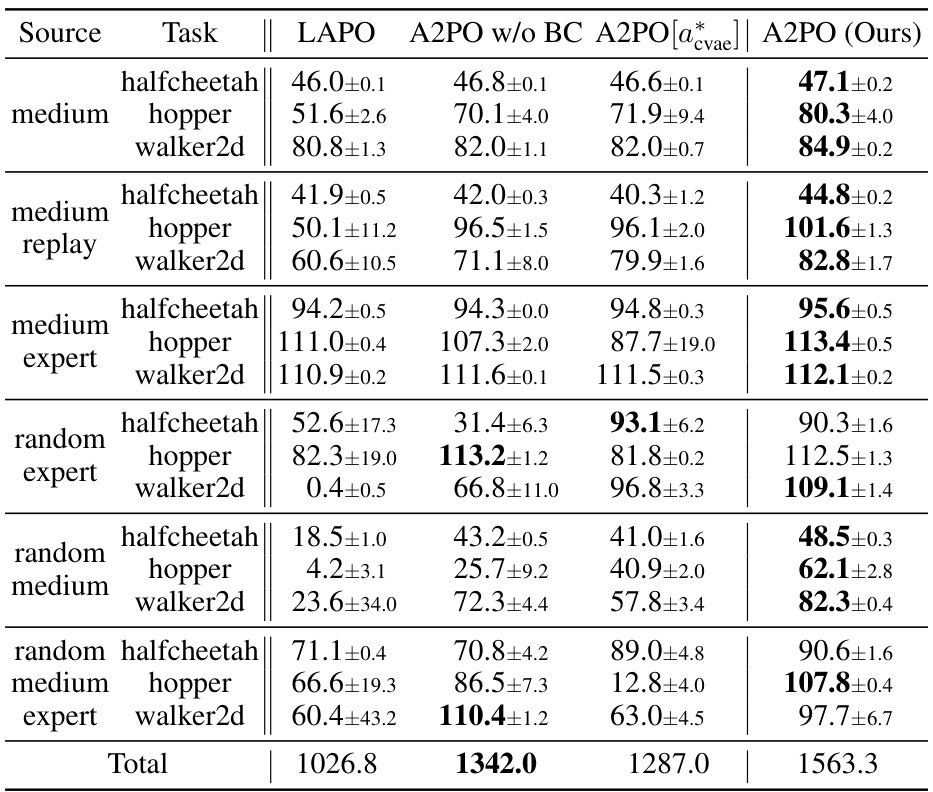
This table presents the test returns achieved by the proposed A2PO method and various baseline methods across different Gym tasks in the D4RL benchmark. The results are averaged over 5 random seeds, and the ± values represent the standard deviation. The performance metric is the normalized score obtained at the final training iteration. Bold values highlight the best-performing method for each task.
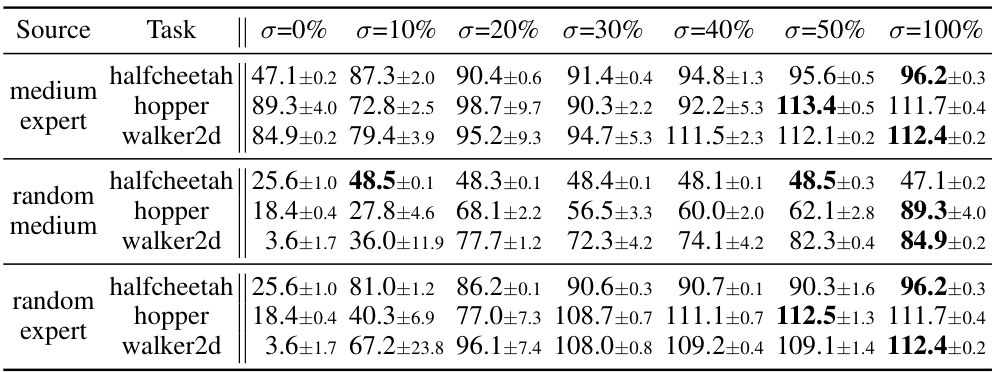
This table presents the test returns achieved by the proposed A2PO method and several baseline algorithms across different Gym tasks within the D4RL benchmark. The results are averaged over five random seeds, with the ± values representing one standard deviation. The performance metric used is the normalized score at the final training iteration. The best performance for each task is highlighted in bold.
Full paper#