Belief-State Query Policies for User-Aligned Planning under Partial Observability

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on user-aligned planning and partially observable environments. It offers a novel framework for incorporating user preferences directly into the planning process, addressing a significant challenge in real-world AI applications. The proposed approach is computationally feasible and shows promising results, paving the way for more user-centered and reliable AI systems.

Visual Insights

#

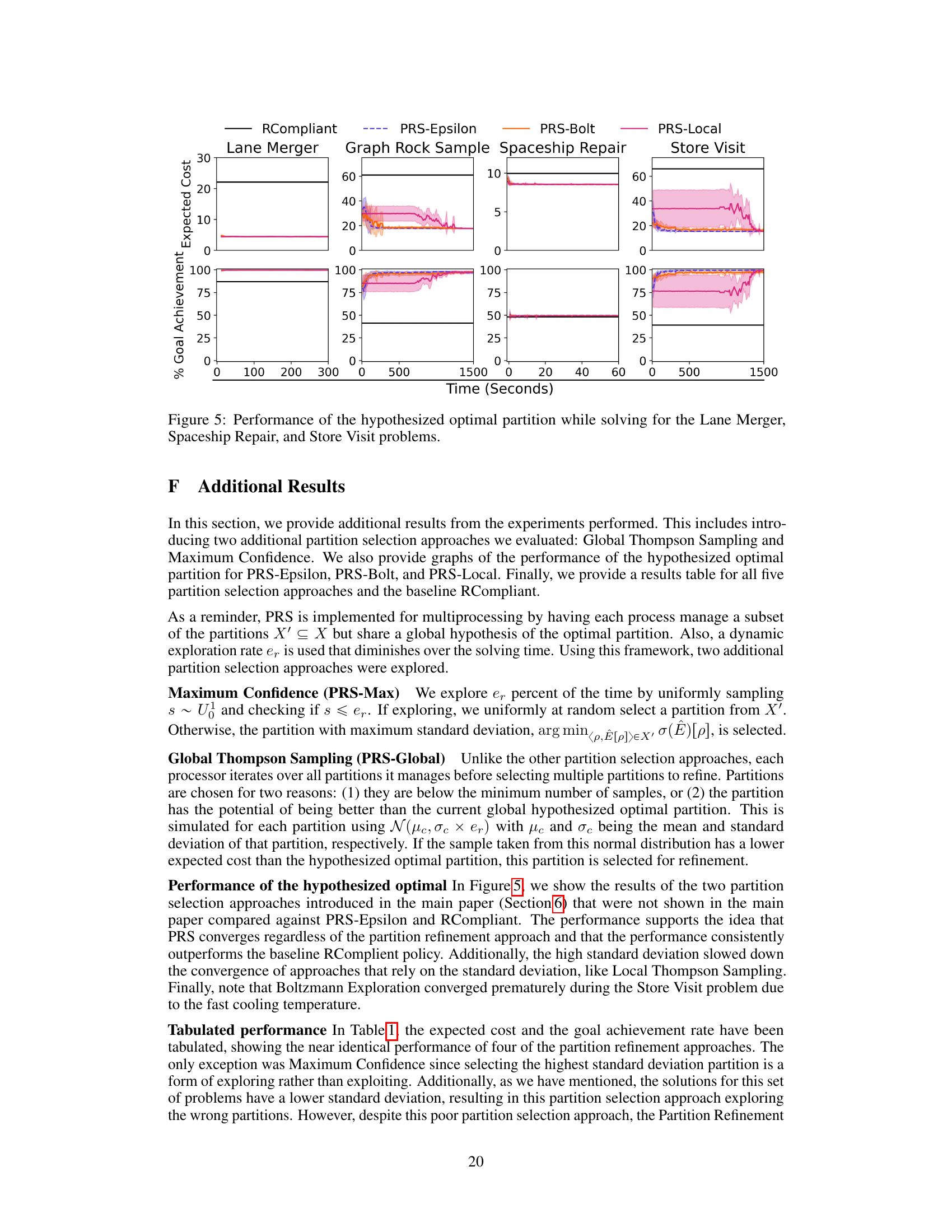
This figure demonstrates a spaceship repair problem where a robot must decide whether to repair itself or the spaceship after a communication error. (a) shows the problem’s structure. (b) presents a belief-state query (BSQ) constraint representing user preferences. The robot should prioritize repairing itself if there’s a high probability of it being broken, and then the spaceship if it’s likely broken. Otherwise, it should wait. (c) shows the non-convex, piecewise constant expected cumulative cost function for this BSQ constraint, illustrating that a finite number of evaluations is sufficient to find optimal user-aligned behavior.

This table presents the performance comparison of the Partition Refinement Search algorithm and the baseline RCompliant method across four different problem domains. It shows the expected cost and goal achievement rate for each algorithm in each problem. The results are based on the average of ten runs for each algorithm and problem domain, with standard deviations included to show variability.

In-depth insights

#

BSQ Framework

#

The BSQ (Belief-State Query) framework offers a novel approach to user-aligned planning in partially observable environments. It cleverly addresses the challenge of expressing user preferences, which often involve high-level descriptions of desired behavior rather than precise reward functions. BSQ constraints directly encode these preferences as queries on the agent’s belief state, thus avoiding the pitfalls of reward engineering in partially observable settings. The framework’s strength lies in its ability to formalize intuitive user requirements into mathematically tractable constraints, paving the way for optimal policy computation. This formalization is crucial because it enables a theoretical analysis of the expected cost function, leading to efficient algorithms that guarantee convergence to optimal user-aligned behavior. The piecewise constant nature of the cost function, despite its non-convexity, is a key theoretical result that underpins the efficacy of the proposed algorithms. The use of strategy trees and the concept of braids elegantly partitions the parameter space, allowing for systematic and efficient exploration of the optimal policy parameters. This approach represents a significant advancement in user-aligned planning, offering a computationally feasible method to achieve true user alignment in complex, uncertain domains.

Piecewise Cost

#

The concept of “Piecewise Cost” in the context of a research paper likely refers to a cost function that exhibits distinct, separable segments. This is in contrast to a smooth, continuously changing cost function. Each segment represents a specific regime or condition, and the cost within a segment might be constant, linear, or follow another simple rule. The transitions between segments are typically sharp, occurring at thresholds or decision points. This structure is particularly relevant in scenarios involving discrete choices or states, such as those frequently encountered in planning problems with partially observable Markov decision processes (POMDPs). The advantage of a piecewise cost function is its computational tractability. While non-convex cost functions are computationally expensive to minimize, piecewise cost functions can often be optimized more efficiently by breaking the problem down into a series of smaller, simpler optimization problems within each segment. This is particularly useful in situations where the cost function is complex or high-dimensional, as it allows for a more manageable and faster solution. The analysis and algorithms to handle such piecewise cost functions would likely form a central contribution of the research. However, a key challenge would be to carefully define the conditions that govern the transitions between the different segments, ensuring that they align with the underlying problem structure and make practical sense.

PRS Algorithm

#

The Partition Refinement Search (PRS) algorithm is a core contribution of the paper, offering a probabilistically complete method for optimizing user-aligned policies within the framework of goal-oriented partially observable Markov decision processes (gPOMDPs). PRS leverages the theoretical result that the expected cost function for belief-state query constraints is piecewise constant, despite being non-convex. This crucial finding transforms the continuous parameter space into a finite set of regions with constant cost, making optimization tractable. The algorithm iteratively refines partitions of the parameter space, sampling leaves of the strategy tree to isolate intervals corresponding to distinct braids (sets of reachable leaves under given policies). This refinement process guarantees convergence to the optimal user-aligned policy as sampling increases. The efficiency of PRS is enhanced through exploration-exploitation strategies for partition selection, and its scalability is demonstrated through empirical evaluation on diverse risk-averse problems. Although the theoretical complexity is linear in the number of leaves, the practical performance is significantly improved by pruning of the strategy tree, leading to improved efficiency in real-world scenarios. The algorithm’s ability to handle complex user preferences makes it a promising tool for building user-aligned AI systems in partially observable domains.

Empirical Results

#

The ‘Empirical Results’ section of a research paper is crucial for validating the claims and demonstrating the practical applicability of the proposed methods. A strong ‘Empirical Results’ section would present a detailed description of the experiments conducted, including the datasets used, the metrics employed, and a clear comparison against relevant baselines. Transparency and reproducibility are paramount, requiring meticulous reporting of experimental setup and parameters. The results should be presented clearly and concisely, typically using tables and figures, showing not only performance metrics but also error bars or confidence intervals to indicate statistical significance. Careful consideration should be given to the selection and interpretation of the evaluation metrics, ensuring that they are appropriate for assessing the specific claims of the paper. Furthermore, a thoughtful discussion of the results is needed. This would involve explaining unexpected findings, addressing potential limitations, and drawing meaningful conclusions about the effectiveness and generalizability of the proposed method. A robust empirical evaluation strengthens the paper’s overall contribution by providing strong evidence of the practical value of the research.

Future Work

#

The paper’s conclusion points towards several promising avenues for future research. Extending BSQ constraints to encompass more expressive capabilities is crucial. Currently limited to first-order logic, incorporating deterministic functions and temporal extensions would greatly broaden their applicability and allow for the encoding of more complex, temporally extended user preferences. The authors also correctly highlight the need to address potential misalignments between user-specified preferences and the underlying gPOMDP objectives. This could involve developing methods to detect and resolve such conflicts automatically, perhaps through more sophisticated analysis techniques or interactive feedback mechanisms. Further exploration into scalable optimization algorithms for complex scenarios is also vital. The paper’s current PRS algorithm, while probabilistically complete, might benefit from enhancements to improve its efficiency in higher dimensional parameter spaces. Finally, developing methods to aid users in expressing their requirements effectively within the BSQ framework warrants attention. This includes user-friendly tools and interfaces that translate high-level preferences into precise BSQ constraints.

More visual insights

#

More on figures

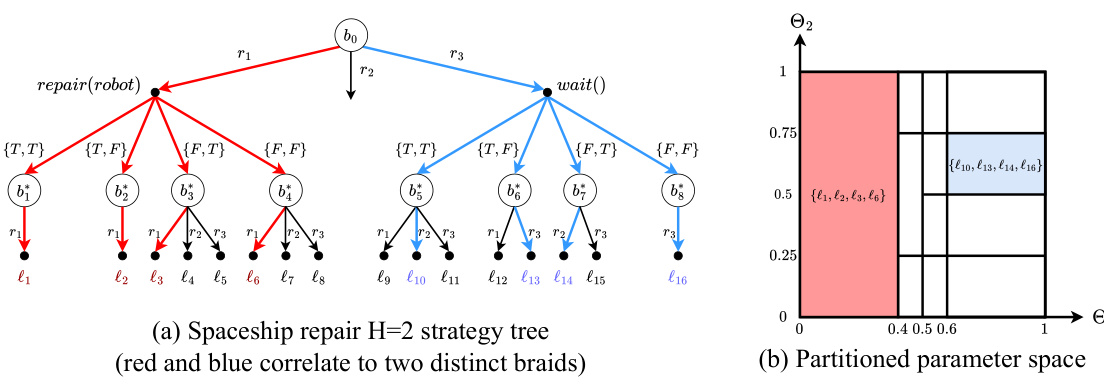
This figure shows a strategy tree and a partitioned parameter space for the Spaceship Repair problem using BSQ constraints. The strategy tree (a) illustrates possible decision paths based on belief states, actions, and observations, with leaf nodes representing final outcomes. Each path through the tree is labelled with a sequence of rules (from the BSQ constraints) and observations. The partitioned parameter space (b) shows how the continuous parameter space for the BSQ constraints is divided into distinct regions, each with a constant expected cost. The color-coding connects the regions in (b) to subsets of leaf nodes in (a), illustrating the relationship between parameter choices and resulting behavior. The sensor accuracy information clarifies the uncertainty involved in the problem.

This figure presents the empirical results of the proposed Partition Refinement Search (PRS) algorithm and compares its performance against several baselines on four different problems: Lane Merger, Graph Rock Sample, Spaceship Repair, and Store Visit. The plot shows the expected cost and percentage of goal achievement over time. The PRS algorithm consistently outperforms the baselines and demonstrates its capability to converge to a high-quality, user-aligned solution. The error bars represent standard deviations, providing a measure of variability in the results.

The figure shows the performance of the Partition Refinement Search (PRS) algorithm compared to Nelder-Mead and Particle Swarm optimization algorithms. The x-axis represents time, and the y-axis shows both expected cost and percentage goal achievement. The results show PRS converging more quickly and achieving a lower expected cost and higher goal achievement rate than the other methods across four different problems: Lane Merger, Graph Rock Sample, Spaceship Repair, and Store Visit. Error bars represent standard deviations.

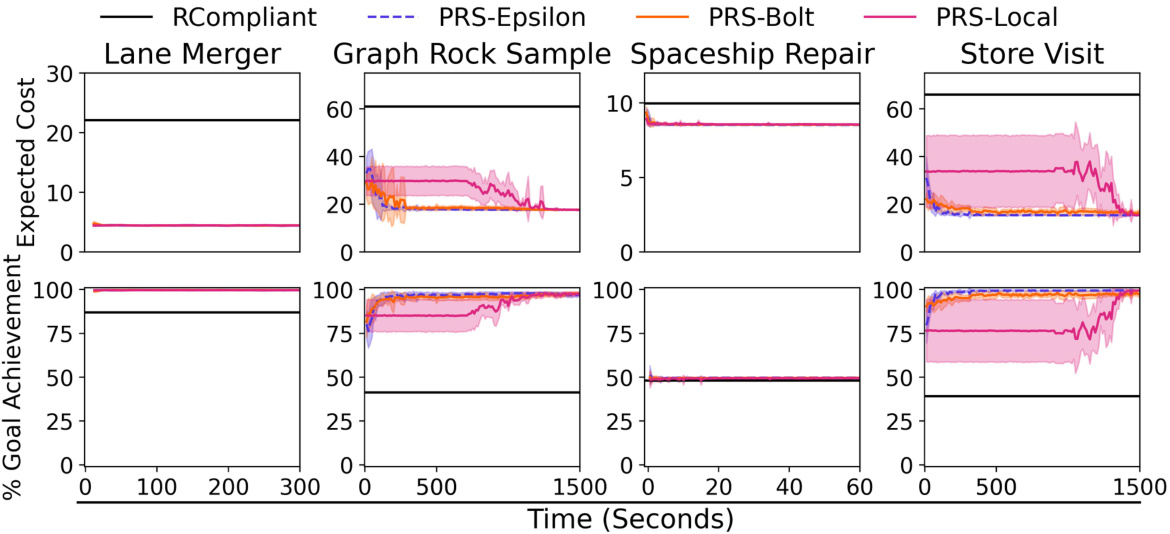
The figure shows the performance of three different algorithms (PRS-Epsilon, Nelder-Mead, and Particle Swarm) over time for four different problems (Lane Merger, Graph Rock Sample, Spaceship Repair, and Store Visit). The y-axis shows both the expected cost and the percentage of goals achieved. The x-axis shows the time in seconds. The plot demonstrates that PRS-Epsilon consistently outperforms the other two algorithms in terms of both expected cost and goal achievement rate across all four problems. Error bars representing standard deviation are included.

Full paper

#