↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Federated learning (FL) aims to train a shared machine learning model across multiple decentralized devices (clients) without directly sharing their data. One-shot FL, which involves a single round of communication, is attractive for its efficiency and privacy but struggles with non-identical data distributions across clients, impacting model accuracy. This paper’s key challenge is to solve the one-shot FL in non-IID data effectively.
The proposed method, FedLPA, addresses this by inferring the statistical properties of each layer in each local model, using a layer-wise Laplace approximation to obtain the posterior. Instead of directly averaging model parameters, FedLPA aggregates these layer-wise posteriors to obtain a more accurate global model. The results across various datasets show that FedLPA significantly outperforms existing one-shot FL methods. This improvement is attributed to FedLPA’s ability to effectively handle data heterogeneity without compromising privacy or communication efficiency.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses the limitations of existing one-shot federated learning methods by proposing a novel approach that significantly improves accuracy, especially in non-IID settings, while maintaining privacy and efficiency. This work contributes to the ongoing research in FL by providing an effective, practical method for real-world applications. It also opens avenues for future research in privacy-preserving one-shot FL and data heterogeneity handling.
Visual Insights#
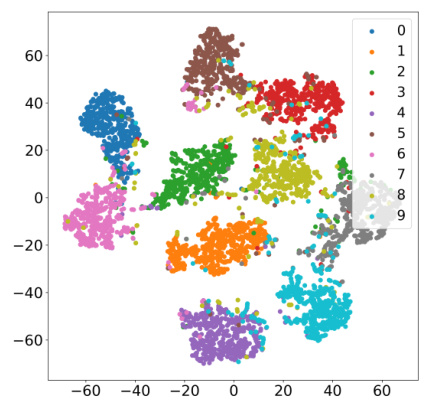
This figure shows the t-SNE visualization of the FedLPA global model trained on the MNIST dataset with a biased data distribution among 10 local clients. The visualization effectively separates the different classes, demonstrating the model’s ability to distinguish between them despite the non-IID data. This highlights the effectiveness of FedLPA in generating a global model that maintains class separability even with heterogeneous local data distributions.

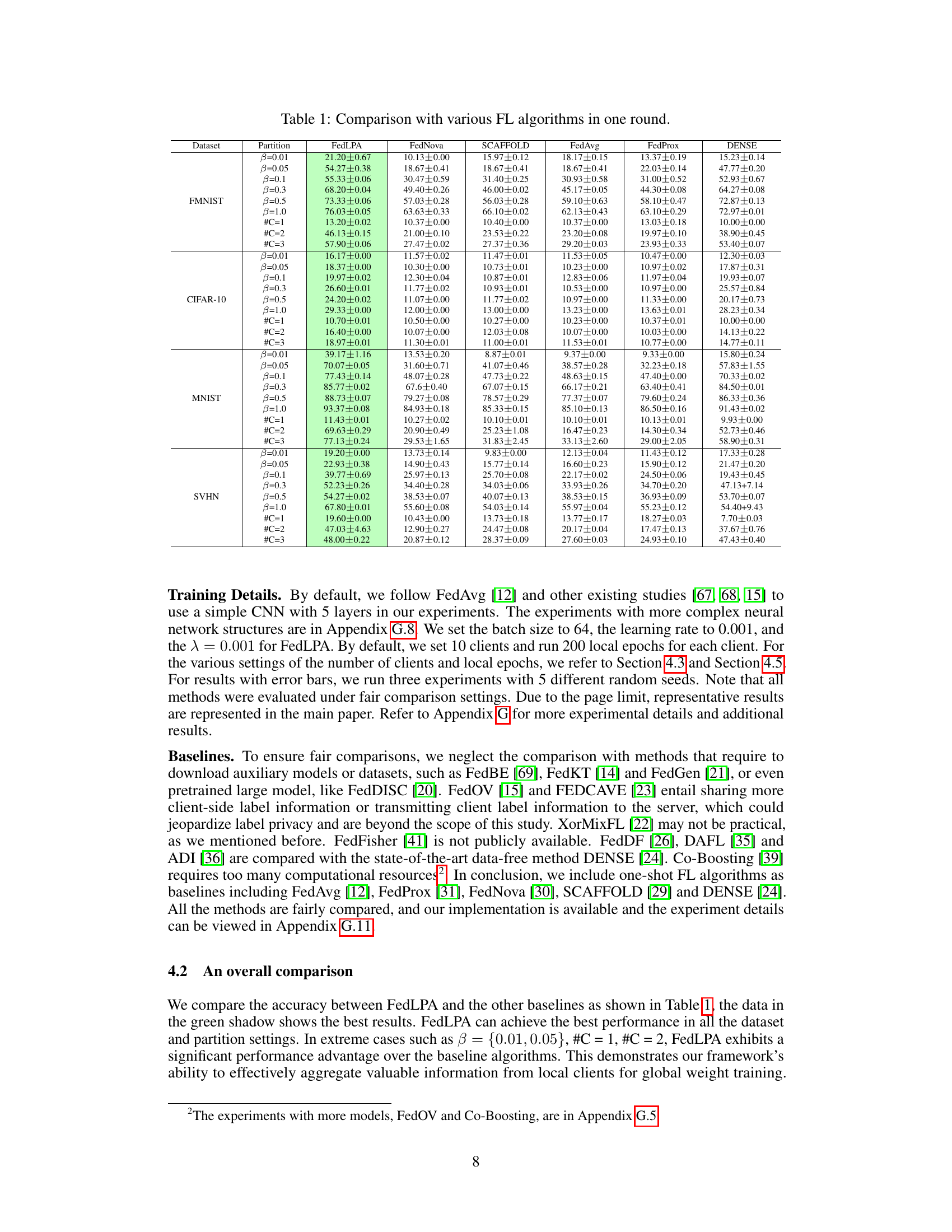
The table compares the performance of FedLPA against several other federated learning algorithms (FedNova, SCAFFOLD, FedAvg, FedProx, and DENSE) across four datasets (MNIST, FMNIST, CIFAR-10, and SVHN) under various data partitioning scenarios (β = {0.01, 0.05, 0.1, 0.3, 0.5, 1.0} and #C = {1, 2, 3}). The results show the test accuracy for each algorithm across different levels of data non-IIDness.
In-depth insights#
One-Shot FL#
One-shot federated learning (FL) represents a significant paradigm shift in federated learning, aiming to drastically reduce communication overhead by limiting client-server interactions to a single round. This approach is particularly appealing in resource-constrained environments or when iterative communication is impractical. However, the inherent challenge lies in effectively aggregating diverse local models trained on non-identical data distributions (non-IID). This heterogeneity significantly impacts the accuracy and convergence of the global model, hence posing a major hurdle for effective one-shot FL. Consequently, research in this area focuses on developing robust aggregation techniques that can effectively handle non-IID data and yield high-performing global models despite the limited communication. This often involves sophisticated statistical methods to account for data biases and differences in local model parameters. While promising, one-shot FL remains an active area of research, with ongoing work focused on overcoming limitations and pushing the boundaries of performance in diverse and challenging scenarios.
Layer-wise Posterior#
The concept of “Layer-wise Posterior” suggests a method for analyzing and aggregating the results from individual layers of a neural network within a federated learning framework. Instead of treating the entire model as a single entity, this approach allows for a more nuanced understanding of how each layer learns and contributes to the overall model’s performance. This layer-by-layer approach offers several key advantages. It provides greater granularity in identifying potential issues with individual layers, leading to more efficient and effective debugging and optimization. By handling each layer separately, this approach could help to mitigate the negative impact of non-identical data distributions across multiple clients, a significant challenge in federated learning. Furthermore, a layer-wise aggregation process might provide better privacy preservation by reducing the amount of sensitive information shared during the aggregation step. This approach is particularly relevant for one-shot federated learning, where communication is limited, and a more efficient aggregation method is essential. However, challenges could arise in managing the complexities of coordinating the posteriors from each layer across different clients. Effectively combining the layer-wise posteriors to create an accurate overall global model is likely to require sophisticated algorithms that are computationally expensive and complex. A critical area of exploration would be exploring the optimization problem, which is likely non-convex, and developing efficient algorithms to guarantee convergence.
FedLPA Method#
The FedLPA method proposes a novel one-shot federated learning approach, focusing on efficient aggregation of locally trained neural networks. Key to FedLPA is its layer-wise posterior aggregation, leveraging Laplace approximations to infer the posterior distribution for each layer in the local models. This approach addresses the challenges of non-identical data distributions among clients by incorporating layer-wise information, thus mitigating the impact of data heterogeneity on the accuracy of the aggregated global model. The method avoids the need for additional datasets or the exposure of private label information, enhancing both accuracy and privacy. FedLPA’s use of block-diagonal empirical Fisher information matrices is also a significant innovation, allowing for efficient computation and aggregation of posterior information, capturing parameter correlations within each layer. This differs from prior approaches that often made simplifying assumptions, leading to potential inaccuracies. The global model parameters are trained efficiently by formulating a convex optimization problem, ensuring a fast convergence rate. FedLPA shows significant improvement over state-of-the-art one-shot methods across various datasets and non-IID scenarios, highlighting the effectiveness and robustness of its layer-wise posterior aggregation technique.
Non-IID Data#
The concept of Non-IID (non-independent and identically distributed) data is crucial in federated learning. It acknowledges that participating clients do not have identical data distributions, a common scenario in real-world applications. This heterogeneity poses significant challenges to model aggregation, as models trained on disparate datasets may produce conflicting updates. The paper likely explores how algorithms must be adapted to accommodate this challenge, potentially focusing on techniques to weight or normalize updates, to leverage the diversity of data while mitigating the negative effects of non-IIDness on model performance and robustness. Strategies like personalized federated learning could be discussed as methods that address the problem explicitly. Furthermore, the paper might investigate the impact of different levels of non-IIDness on the outcome, perhaps by varying the data distribution imbalance across datasets. Ultimately, a deep understanding of non-IID data is vital for the successful and accurate development of federated learning systems.
Privacy Concerns#
The research paper’s discussion of privacy is crucial given the sensitive nature of federated learning. The authors acknowledge the inherent risk of data breaches and privacy violations in federated learning systems. Their proposed FedLPA method aims to mitigate these risks by avoiding the transmission of private labels or data distributions. However, the paper also notes that FedLPA’s privacy level is comparable to existing federated learning algorithms, implying susceptibility to known attacks. The paper suggests the possibility of integrating FedLPA with additional privacy-enhancing techniques like differential privacy to further bolster data security. A comprehensive analysis of potential vulnerabilities, specific attack vectors, and the effectiveness of these mitigation strategies would strengthen the paper’s contribution to the field of privacy-preserving machine learning. Future work should include a more detailed exploration of FedLPA’s resilience against various privacy attacks and a comparative study demonstrating its improved privacy performance over existing methods.
More visual insights#
More on figures
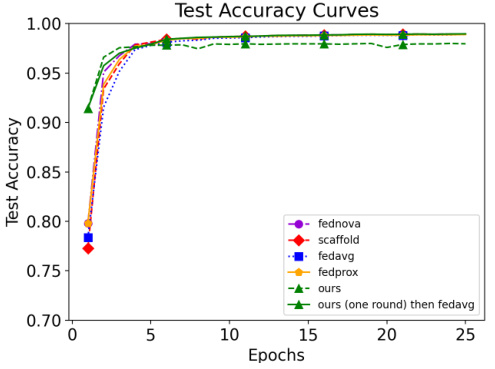
This figure shows the test accuracy curves for FedLPA and other baseline methods (FedAvg, FedNova, SCAFFOLD, and FedProx) over multiple rounds on the MNIST dataset. FedLPA achieves the highest accuracy in the first round, demonstrating its strong one-shot learning capabilities. While its performance improves with additional rounds, it does so more slowly than the other methods. The figure also shows the accuracy of using FedLPA for one round followed by FedAvg for the subsequent rounds, suggesting a hybrid approach that combines the strengths of both methods.
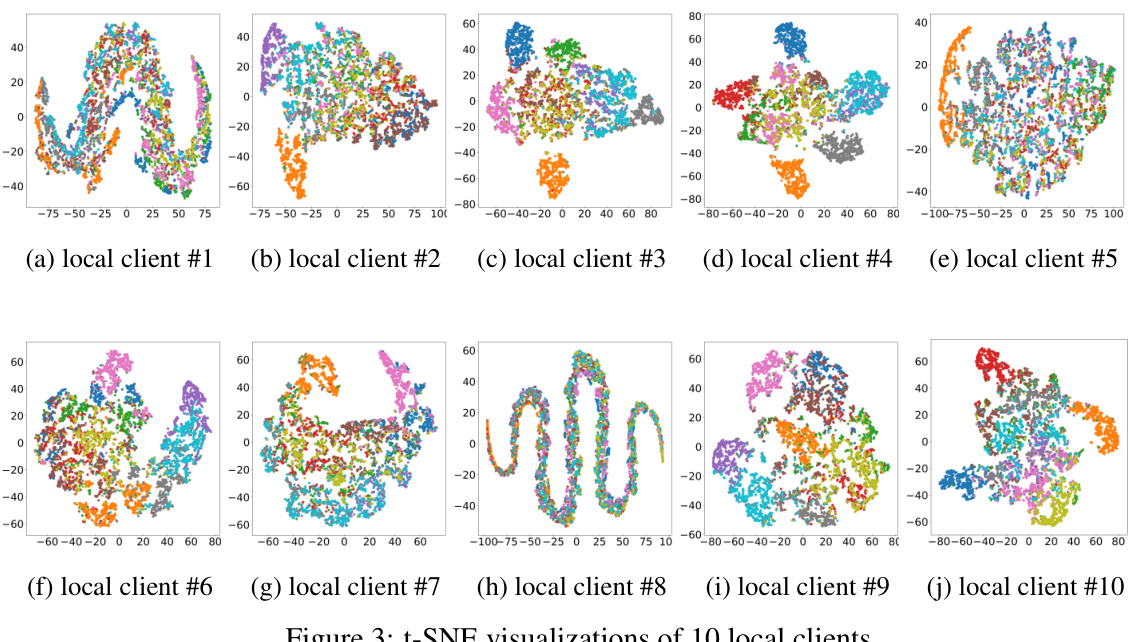
This figure shows the t-SNE visualizations of the data from 10 different local clients. Each subplot represents a different client’s data, showing how the data points cluster based on their labels. The visualizations highlight the non-IID nature of the data across different clients, with some clients having data points concentrated in specific areas of the t-SNE space while others are more spread out. This illustrates the challenge of aggregating models from diverse clients in federated learning.
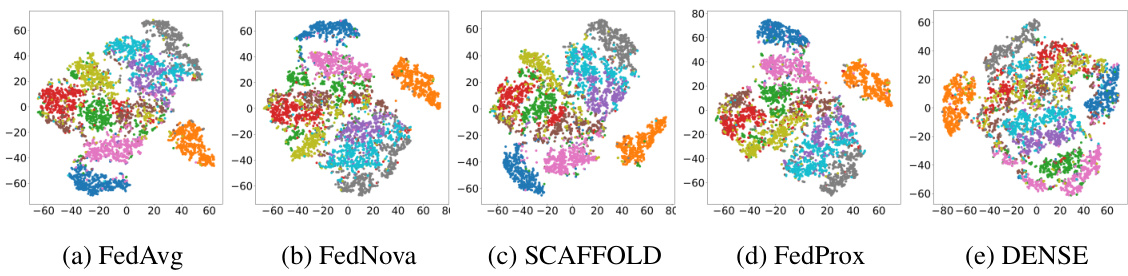
This figure shows the t-distributed Stochastic Neighbor Embedding (t-SNE) visualization of the global model generated by FedLPA on the MNIST dataset. The data used for training was non-IID, meaning it had a biased distribution across the 10 local clients. The plot demonstrates that the FedLPA global model effectively separates the different classes of handwritten digits, indicating good classification performance even with non-IID data.
More on tables
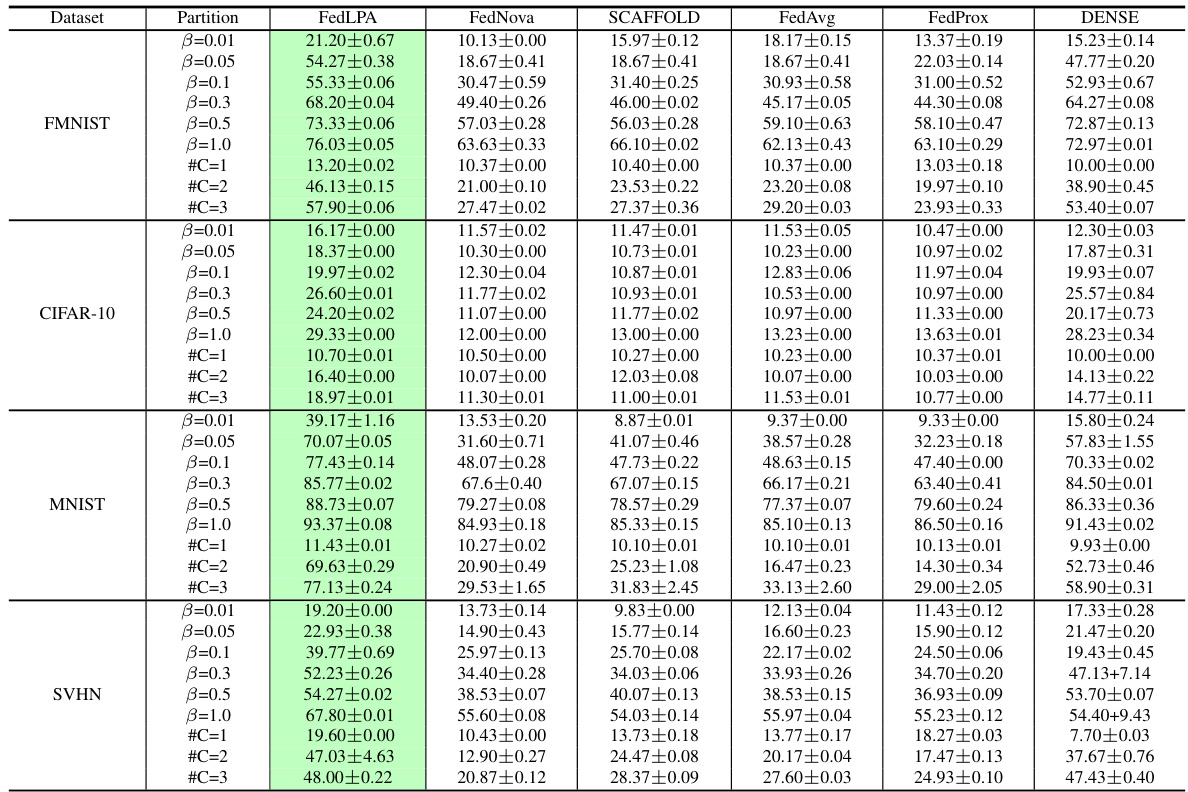
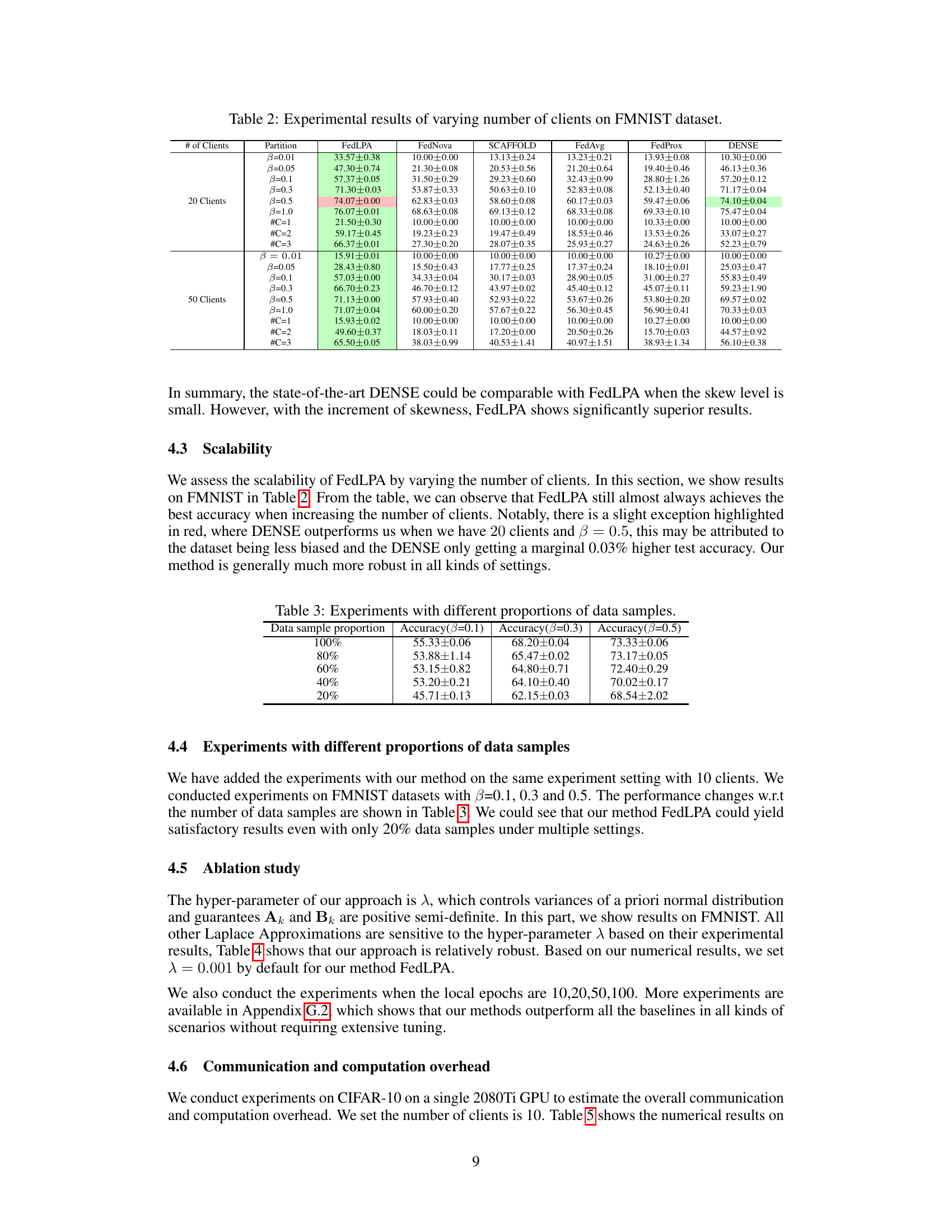
This table compares the performance of FedLPA against several other federated learning algorithms across four datasets (FMNIST, CIFAR-10, MNIST, SVHN). The comparison is done for various non-IID data settings. Different data partitioning methods, labeled as #C=k (where k is the number of classes per client) and β=x (where x is a parameter representing the degree of data skew), are used to simulate realistic non-IID scenarios. The table shows the test accuracy achieved by each algorithm under each condition, highlighting FedLPA’s performance.
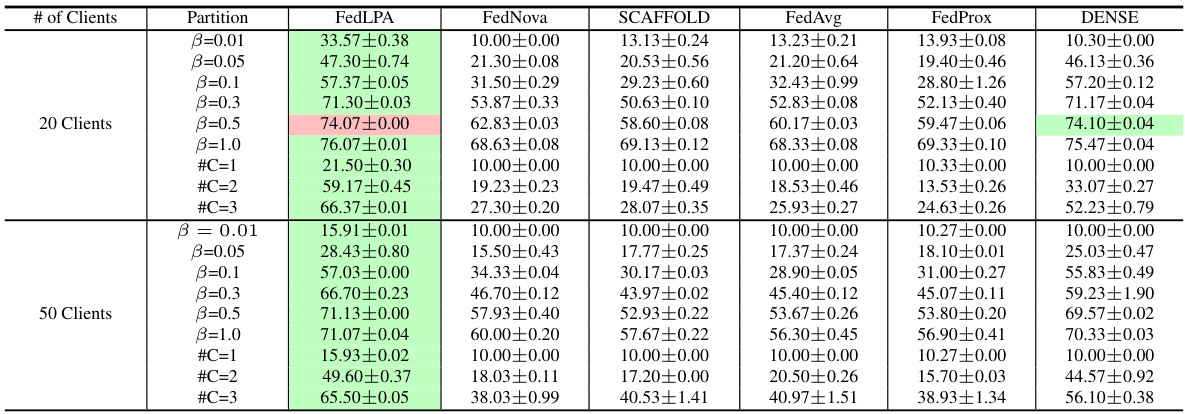
The table compares the performance of FedLPA with several other federated learning algorithms across four datasets (MNIST, FMNIST, CIFAR-10, and SVHN). Each dataset is partitioned using two different non-IID approaches (β and #C). The performance metrics (accuracy) are reported with standard deviations for each algorithm and data partition method. This demonstrates FedLPA’s performance relative to existing state-of-the-art one-shot federated learning approaches.
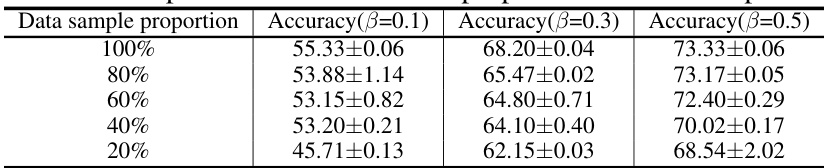
This table shows the impact of reducing the amount of data used for training on the model’s accuracy. The results are presented for different levels of data skew (beta values of 0.1, 0.3, and 0.5). Each row shows the accuracy achieved when using a specific percentage of the original dataset (100%, 80%, 60%, 40%, and 20%). The table demonstrates how the model’s performance is affected as the amount of training data decreases.
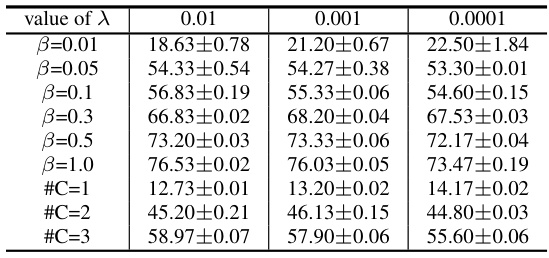
This table presents the experimental results obtained by varying the hyperparameter λ in the FedLPA model. The results show test accuracy for different levels of label skew (β) and data partitioning (#C), demonstrating the robustness of the FedLPA approach to changes in λ. The results are presented in the form of mean ± standard deviation of test accuracy over multiple experimental runs.

This table presents the communication and computation overhead for various federated learning algorithms (FedLPA, FedNova, SCAFFOLD, FedAvg, FedProx, and DENSE) when applied to a simple CNN with 5 layers on the CIFAR-10 dataset. The ‘Overall Computation’ column shows the total computation time in minutes, and the ‘Overall Communication’ column indicates the total communication overhead in MB. The results highlight the computational and communication efficiency trade-offs among these algorithms.

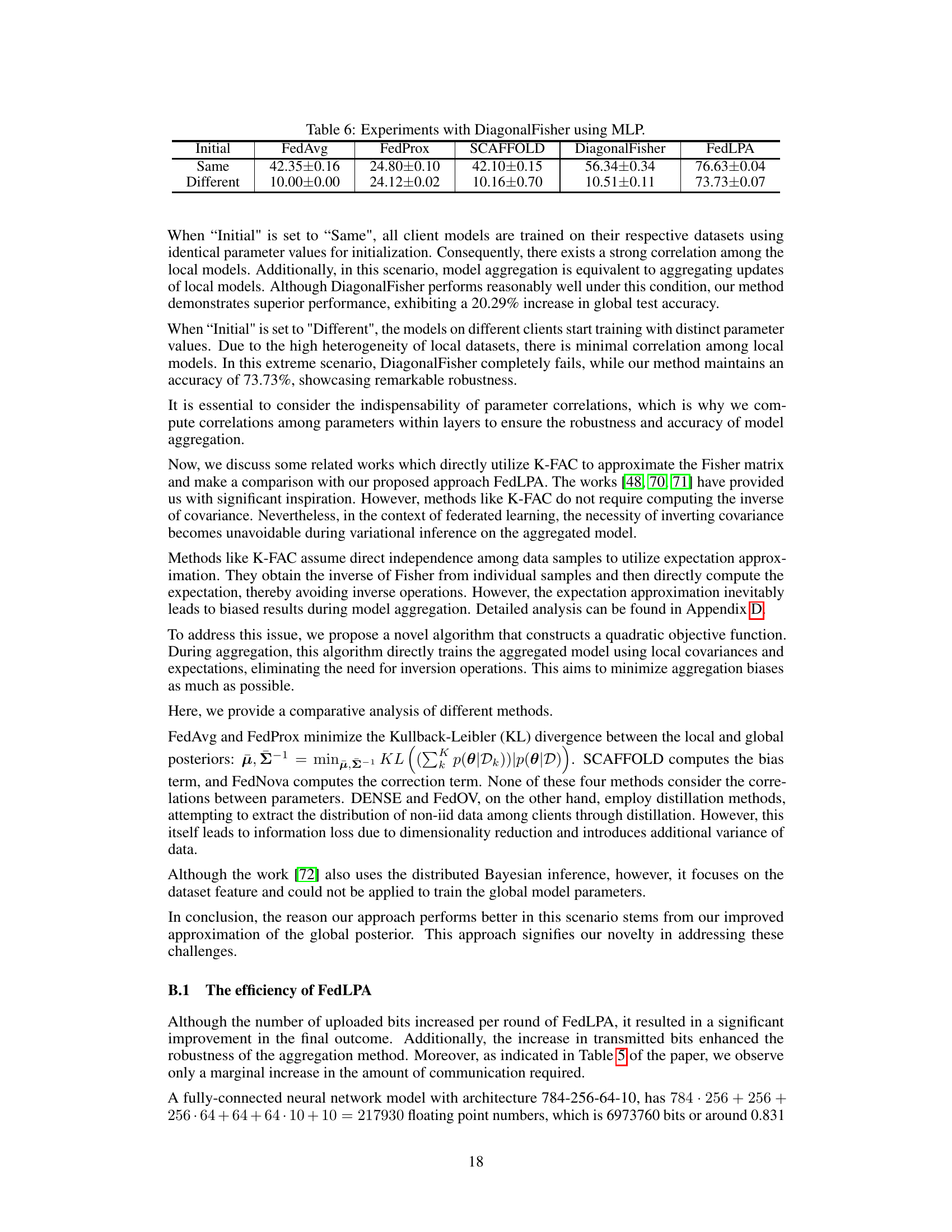
This table compares the performance of FedAvg, FedProx, SCAFFOLD, DiagonalFisher, and FedLPA on an MLP model under two different initialization schemes for client models: ‘Same’ (same initial parameters) and ‘Different’ (different initial parameters). The results show that FedLPA outperforms the other methods, particularly when the client models have different initializations. This highlights the effectiveness of FedLPA in handling non-IID data distributions.

This table compares the performance of FedLPA and DiagonalFisher on an MLP model under two different initialization scenarios: ‘Same’ (models initialized with the same parameters) and ‘Different’ (models initialized independently). The results highlight FedLPA’s superior robustness to data heterogeneity, particularly when the models are initialized differently, showcasing a significant performance improvement over DiagonalFisher.
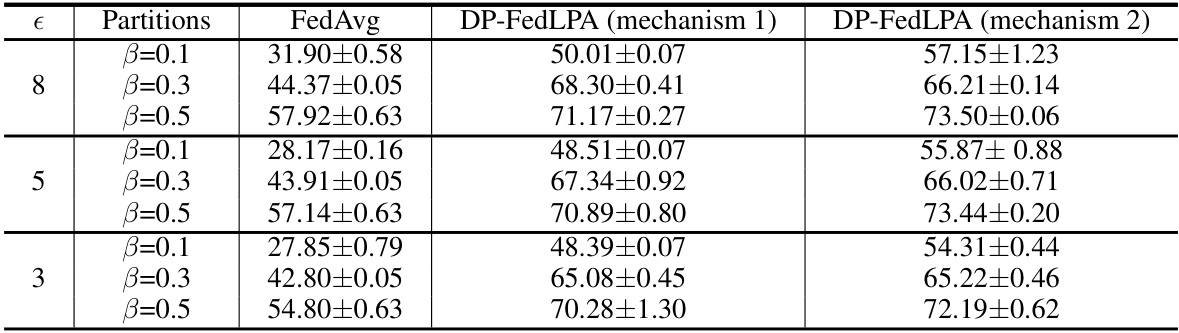
This table presents the results of experiments conducted to evaluate the performance of FedLPA with two different differential privacy mechanisms. The experiments were performed using the MNIST dataset with various data partitioning settings (β = 0.1, 0.3, 0.5) and different privacy levels (ε = 3, 5, 8). The table compares the accuracy of FedLPA with the two privacy mechanisms against the accuracy of the standard FedAvg algorithm. The results demonstrate the impact of different privacy parameters on the accuracy of the FedLPA algorithm under various data distribution settings.
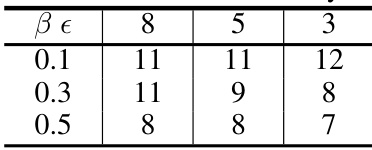
This table shows the number of rounds needed for DP-FedAvg to achieve a similar test accuracy as FedLPA with the first differential privacy mechanism for different beta and epsilon values. It demonstrates the efficiency of FedLPA as a one-shot method compared to DP-FedAvg which requires multiple rounds.

This table presents the results of iDLG attacks on FedLPA and FedAvg, showing the mean squared error (MSE) between the original and reconstructed images at various percentiles. It aims to evaluate and compare the privacy-preserving capabilities of the two methods by measuring their resistance to reconstruction attacks. Higher MSE values indicate stronger privacy protection.
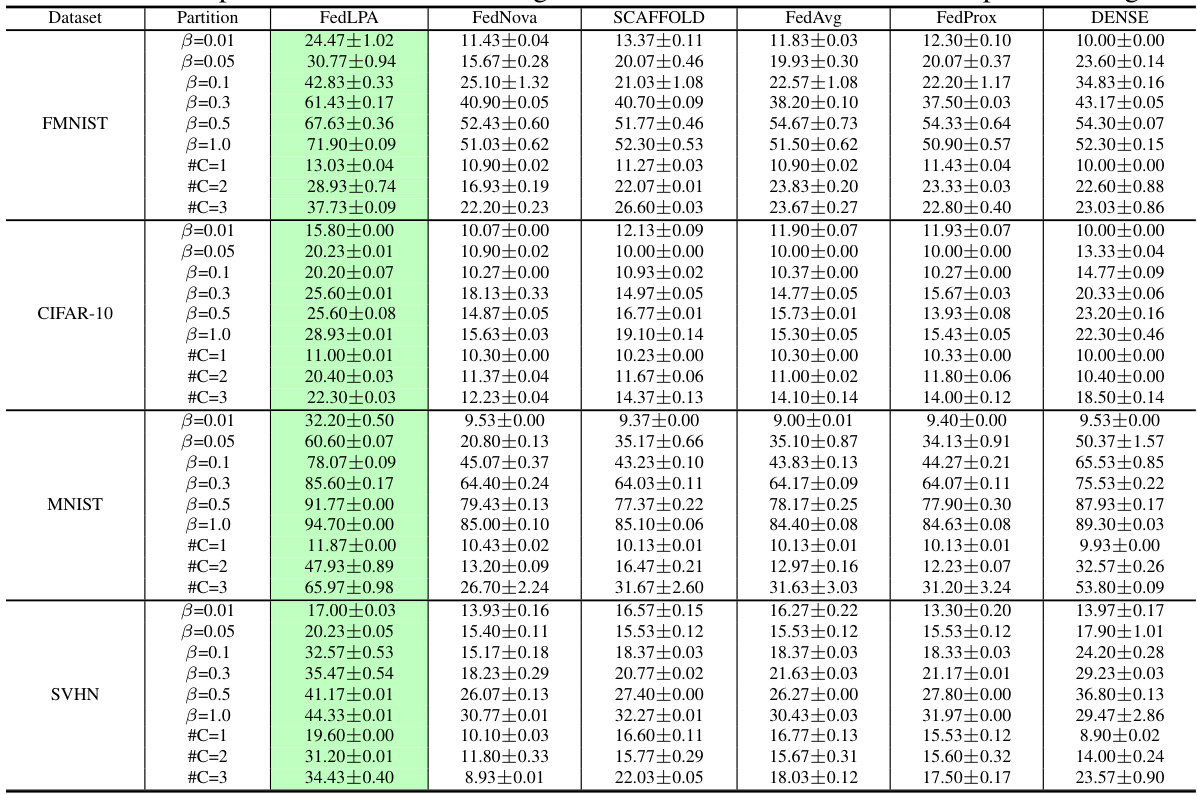
This table presents a comparison of the proposed FedLPA algorithm with several existing federated learning (FL) algorithms. The comparison is done using various datasets (FMNIST, CIFAR-10, MNIST, SVHN) under different data partitioning methods (β = 0.01, 0.05, 0.1, 0.3, 0.5, 1.0 and #C = 1, 2, 3) representing various levels of non-IID data distribution. The results show the test accuracy achieved by each algorithm in a single communication round (one-shot FL). This table highlights the superior performance of FedLPA across different datasets and non-IID settings.

The table compares the performance of FedLPA with other federated learning algorithms (FedAvg, FedProx, FedNova, Scaffold, and DENSE) on four benchmark datasets (MNIST, FMNIST, CIFAR-10, and SVHN) under various non-IID data settings. The non-IID settings are controlled by the parameters β and #C. β represents the Dirichlet distribution parameter for label skew, and #C indicates the number of classes per client. The table shows the test accuracy for each method under these different conditions, allowing for a direct comparison of the performance of FedLPA against state-of-the-art baselines.
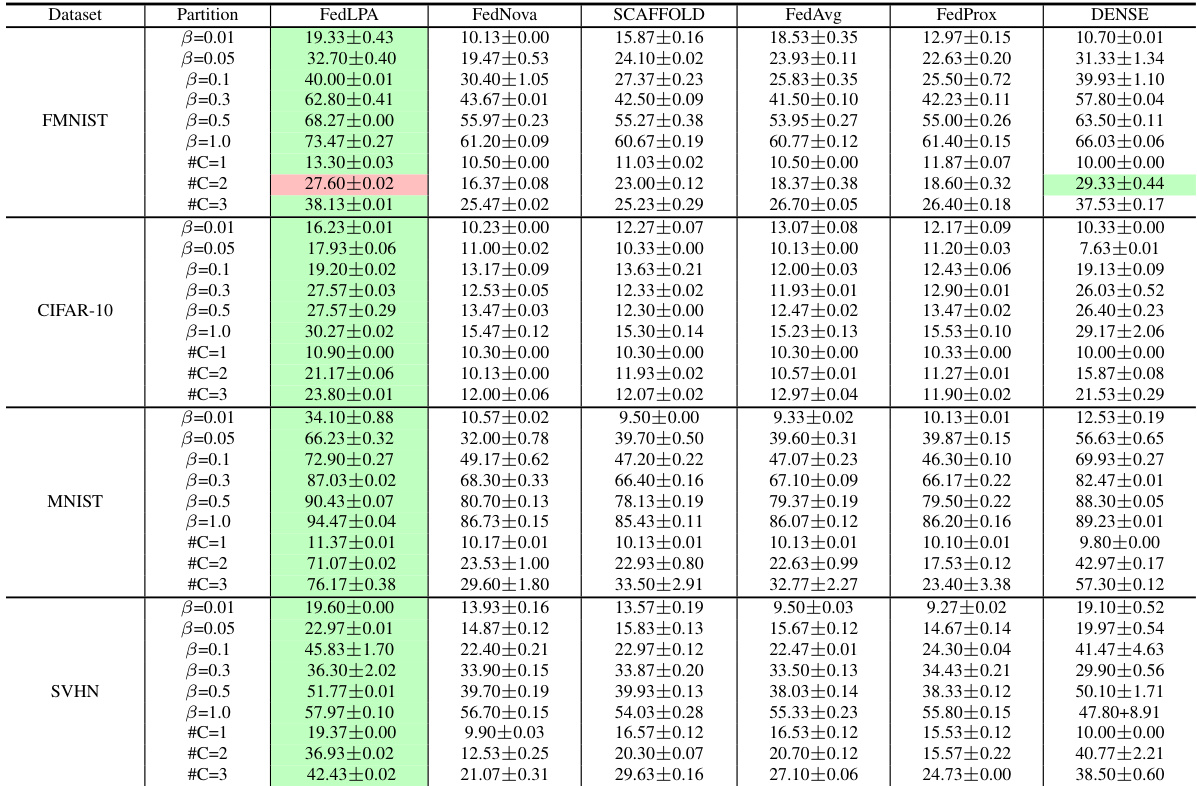
The table compares the performance of FedLPA against several other federated learning algorithms on four different datasets (MNIST, FMNIST, CIFAR-10, and SVHN) under various non-IID data settings. Different non-IID settings are simulated by varying the number of classes per client (#C) and by controlling the class distribution skew using the Dirichlet distribution parameter (β). The results show FedLPA’s accuracy across different metrics and non-IID settings.

This table compares the performance of the proposed FedLPA algorithm against several other federated learning (FL) algorithms on four different datasets (MNIST, Fashion-MNIST, CIFAR-10, and SVHN) under various data partitioning strategies to simulate different levels of non-IID data. The results show the test accuracy of each algorithm on each dataset and partitioning scenario. It highlights how FedLPA performs in different non-IID scenarios compared to the baselines.

This table compares the performance of FedLPA against several other federated learning algorithms across various datasets and data partitioning schemes (IID and non-IID). It shows the test accuracy achieved by each algorithm under different levels of data heterogeneity. The results highlight FedLPA’s superior performance, particularly in non-IID scenarios with high label skewness.
The table compares the performance of FedLPA with several other federated learning algorithms across various datasets and non-IID data settings. It shows test accuracy results for different levels of data heterogeneity, represented by β values and #C values, which indicate the degree of label skew in the data.

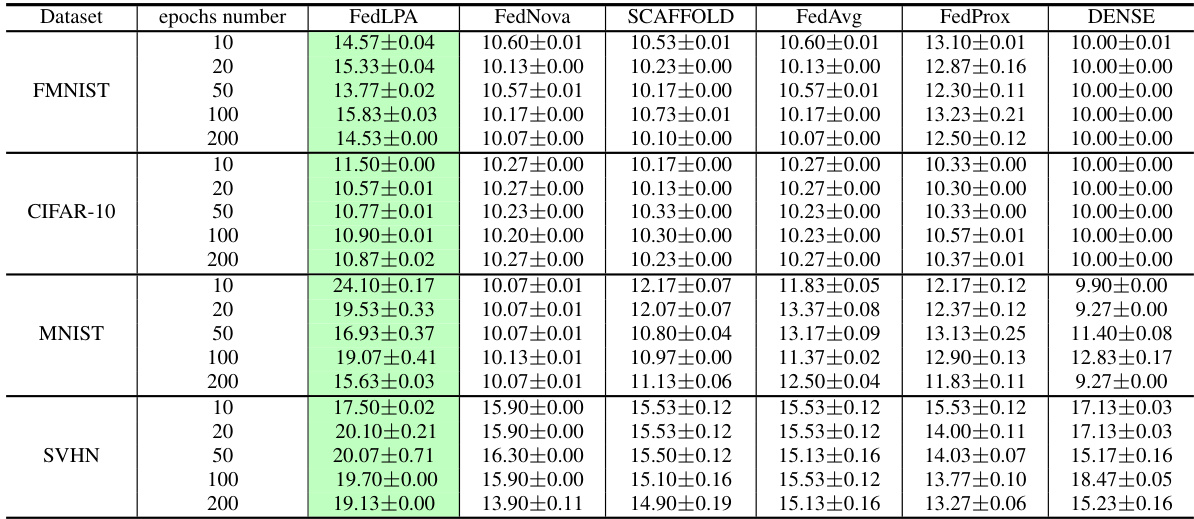
This table compares the performance of FedLPA and FedOV on the MNIST dataset with a non-IID data distribution where each client only has data from 2 classes. The results show how the accuracy of both methods changes with varying numbers of local epochs (10, 20, 50, 100, 200). FedOV transmits label information, while FedLPA does not. The green highlights indicate where FedLPA outperforms FedOV.

This table compares the performance of FedLPA against several other federated learning algorithms across different datasets and non-IID data distributions. The results show accuracy for various settings defined by the beta parameter (β) and the number of classes per client (#C). Higher values generally indicate better performance. The table highlights FedLPA’s effectiveness, especially in challenging non-IID scenarios.

This table compares the performance of FedLPA against several other federated learning algorithms on four different datasets (MNIST, FMNIST, CIFAR-10, and SVHN) under various non-IID data settings. The performance is measured across several metrics and different levels of data heterogeneity, represented by parameters β and #C, indicating the degree of label imbalance or class distribution skew among the clients. The results demonstrate FedLPA’s superior performance, especially in extreme non-IID scenarios.

This table compares the performance of FedLPA with several other federated learning algorithms on four different datasets (MNIST, Fashion-MNIST, CIFAR-10, and SVHN) under various non-IID data settings. The non-IID settings are simulated using two different partitioning methods to introduce varying levels of label skew: one where each client only has data from a subset of classes (#C=k), and another where the class distribution is sampled from a Dirichlet distribution (pk~Dir(β)). The table shows the test accuracy achieved by each algorithm under each data setting, highlighting the superior performance of FedLPA, particularly in scenarios with high label skew.

This table presents the results of experiments conducted using the VGG-9 model. It compares the performance of FedLPA against several other federated learning algorithms (FedNova, SCAFFOLD, FedAvg, FedProx, and Dense) under different levels of data heterogeneity (β = 0.1, 0.3, and 0.5). The results are presented as the average test accuracy with standard deviation, demonstrating the superior performance of FedLPA across varying levels of data heterogeneity. Note that VGG-9 is a deeper and more complex model than the CNNs used in other parts of the experiments.
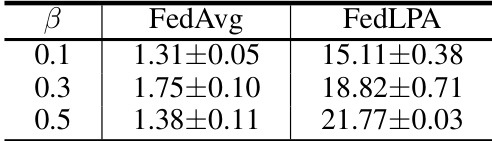
This table presents the experimental results of FedLPA on the CIFAR-100 dataset. It shows the accuracy achieved by FedLPA for different levels of data heterogeneity (β values of 0.1, 0.3, and 0.5). The results are likely compared against other federated learning methods, demonstrating FedLPA’s performance on a more challenging dataset with a larger number of classes.
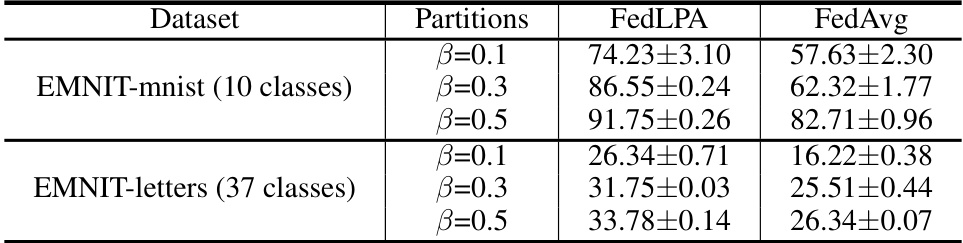
This table presents the results of experiments conducted on the EMNIST dataset using the FedLPA and FedAvg algorithms. It shows the accuracy achieved under different data partition settings (β=0.1, 0.3, 0.5) for two variations of the EMNIST dataset: one with 10 classes (EMNIT-mnist) and one with 37 classes (EMNIT-letters). The results highlight the performance improvement of FedLPA over FedAvg, demonstrating its effectiveness particularly in scenarios with non-IID data.
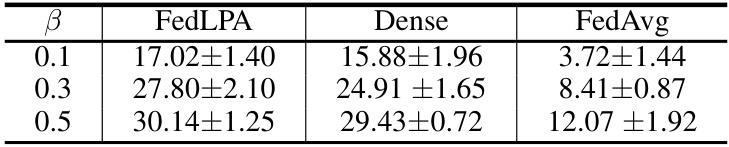
This table presents the results of experiments conducted using the ResNet-18 model on the Tiny-ImageNet dataset. The experiments compare the performance of FedLPA against FedAvg and Dense, across different levels of data heterogeneity (represented by the beta parameter, β). The results show the accuracy achieved under various levels of data heterogeneity. Higher beta values indicate less heterogeneity and a higher overall accuracy.

This table presents the results of an ablation study on the number of approximation iterations used in FedLPA. It shows that increasing the number of iterations generally improves accuracy, but the gains diminish beyond a certain point. The results are shown for different data skewness levels (β=0.1, 0.3, 0.5). The computation time also increases linearly with the number of iterations.
Full paper#