↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current novel view synthesis methods struggle with sparse viewpoints, often relying on external semantic or depth priors for optimization. However, diffusion models, which offer direct visual supervision, underperform due to low information entropy in sparse data, leading to mode deviation during optimization. This creates a need for methods that effectively leverage diffusion priors under such challenging conditions.
The paper proposes Inline Prior Guided Score Matching (IPSM), which addresses this challenge. IPSM uses visual inline priors (from pose relationships) to adjust the rendered image distribution. It decomposes the original optimization objective of Score Distillation Sampling, enabling effective diffusion guidance without any additional training. The IPSM-Gaussian pipeline, integrating IPSM with 3D Gaussian Splatting, further enhances performance by adding depth and geometry consistency regularization. Experiments demonstrate state-of-the-art reconstruction quality on various datasets.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses a critical challenge in 3D reconstruction: novel view synthesis under sparse views. It introduces a novel method, improving upon existing techniques that struggle with limited data. This opens avenues for advancements in various applications, including augmented reality and virtual reality, where high-quality 3D models are crucial but data acquisition can be expensive or challenging.
Visual Insights#
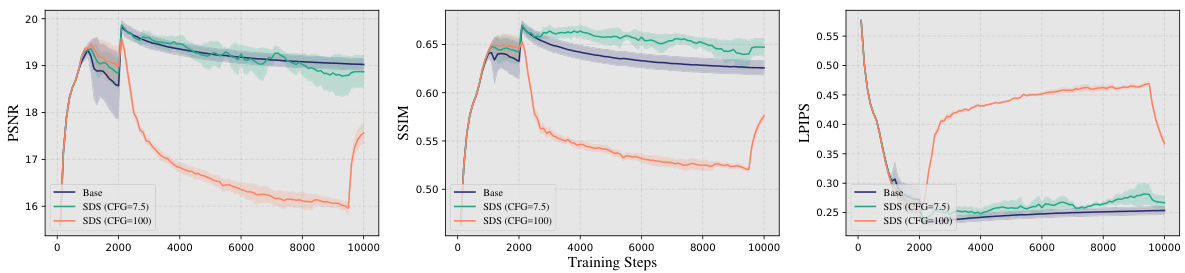
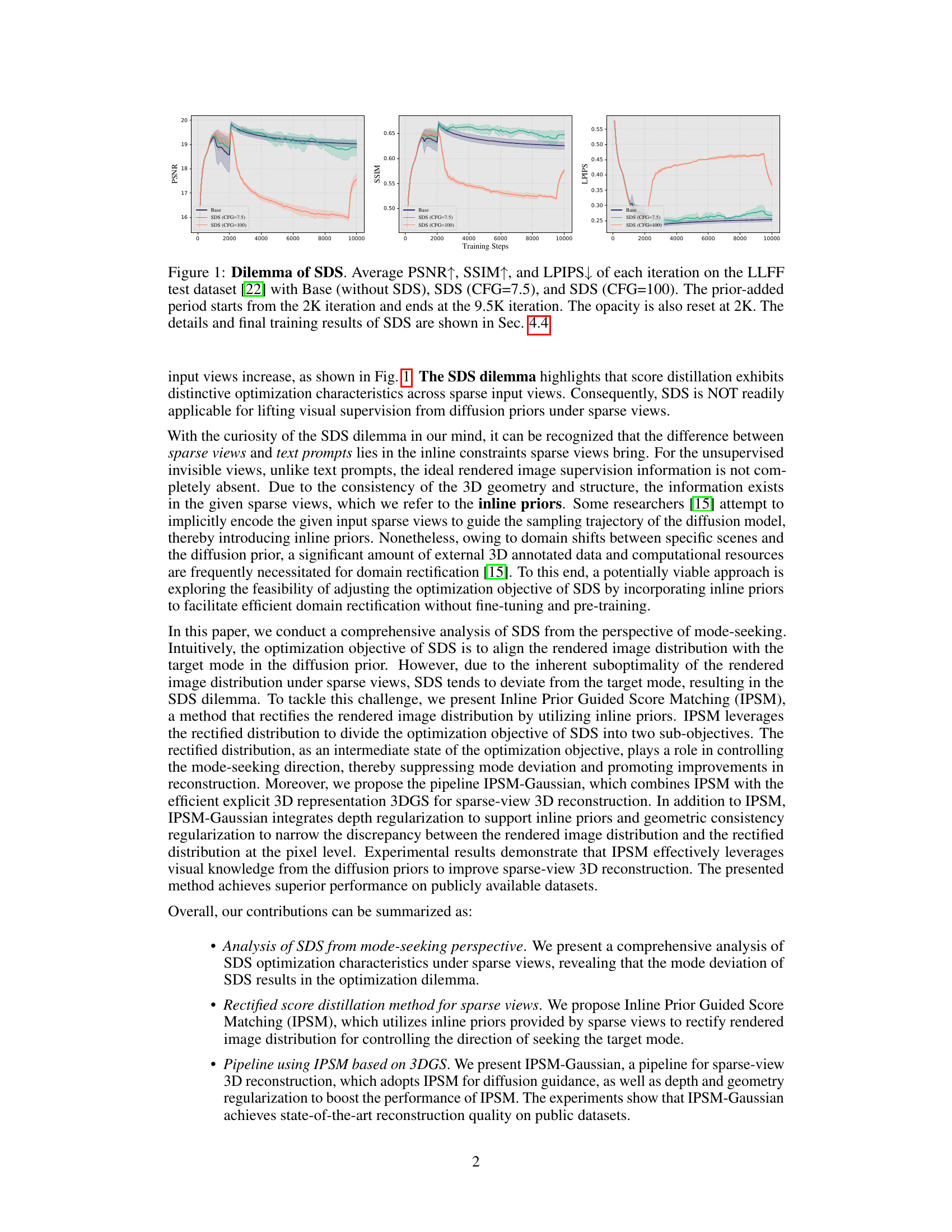
This figure shows the performance of Score Distillation Sampling (SDS) on the LLFF dataset during training. It compares three settings: a baseline without SDS, SDS with a configuration factor (CFG) of 7.5, and SDS with a CFG of 100. The graphs display PSNR (higher is better), SSIM (higher is better), and LPIPS (lower is better) over training iterations. The results highlight a performance issue with SDS under sparse views (the ‘SDS dilemma’), where the addition of the diffusion prior doesn’t improve results, and can even hinder them. This issue is most evident in the CFG=100 case. The figure indicates that the use of a diffusion prior via SDS is not directly beneficial for novel view synthesis from sparse views.
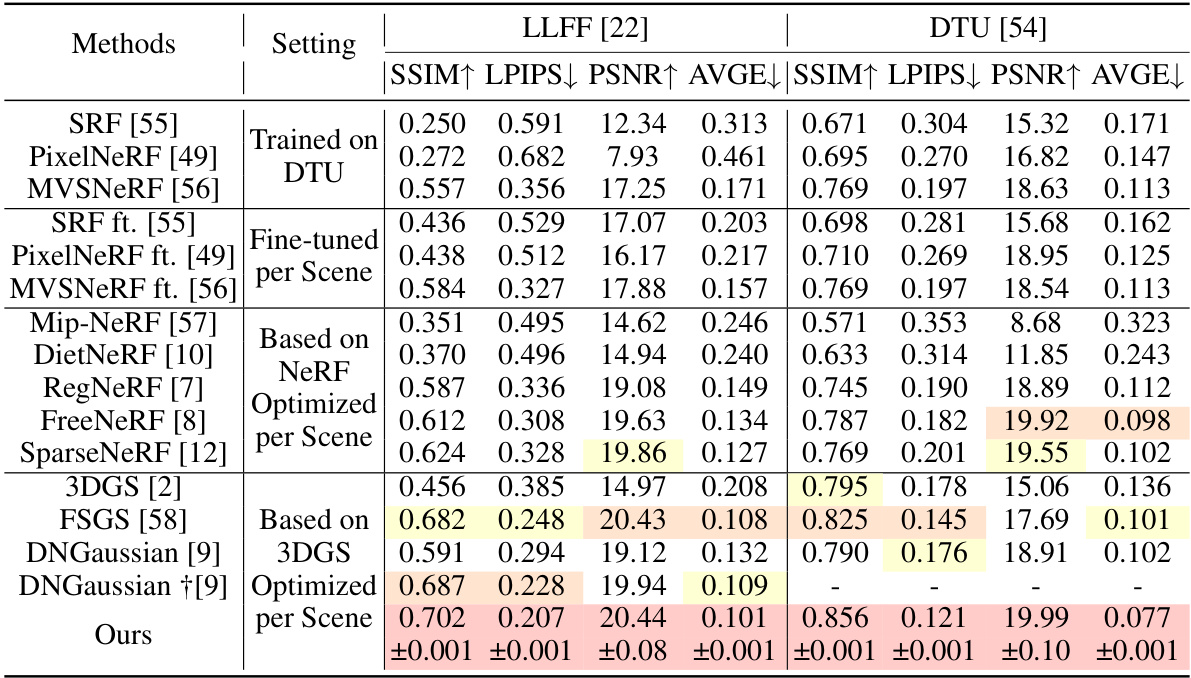
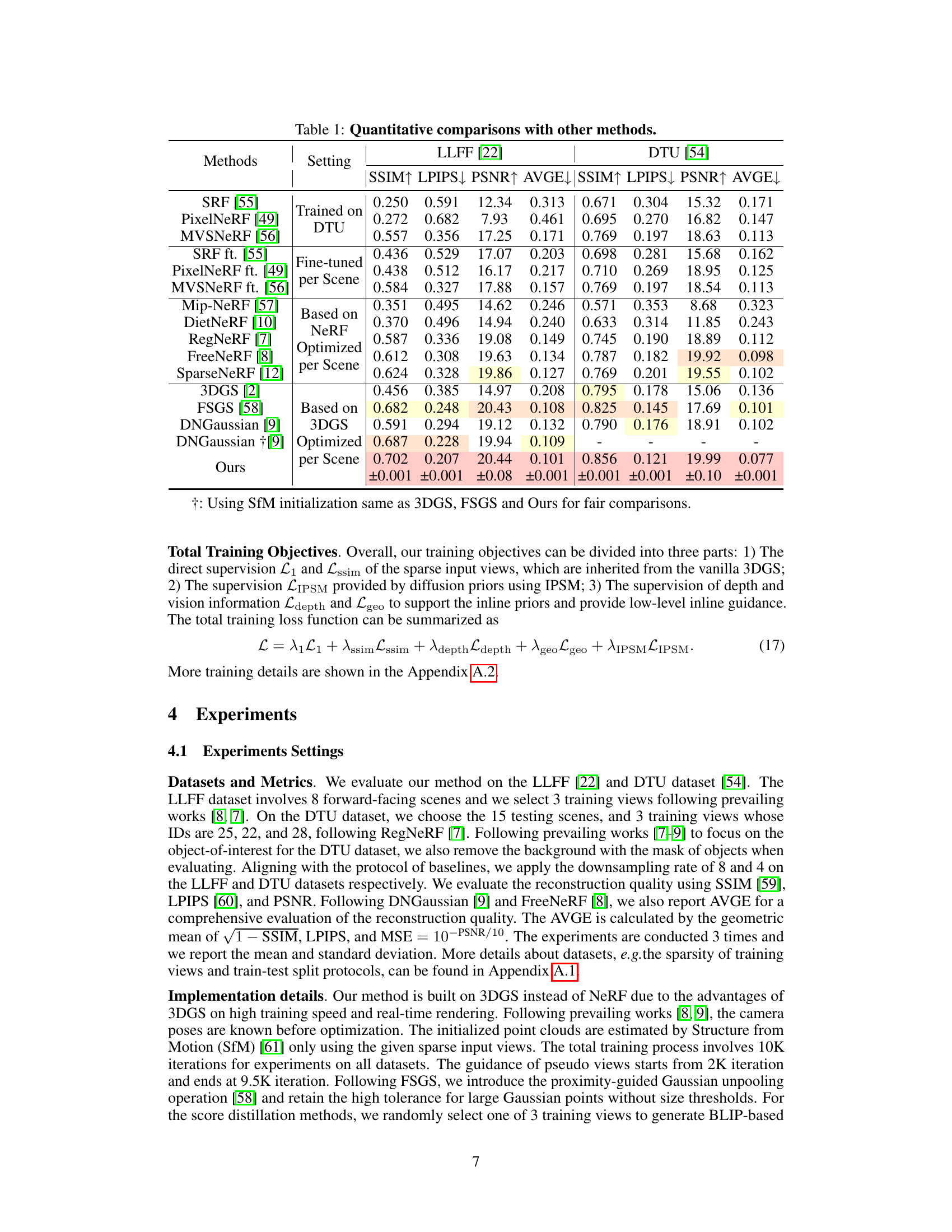
This table presents a quantitative comparison of the proposed IPSM-Gaussian method with several other state-of-the-art novel view synthesis methods on the LLFF and DTU datasets. The comparison includes metrics such as SSIM, LPIPS, PSNR, and AVGE, providing a comprehensive evaluation of reconstruction quality under different settings (trained on DTU, fine-tuned, based on NeRF, optimized, per scene). This allows for a direct assessment of the performance gains achieved by the proposed approach.
In-depth insights#
Sparse View NVS#
Sparse View Novel View Synthesis (NVS) presents a significant challenge in 3D reconstruction due to the limited information available from few viewpoints. Traditional NVS methods, trained on dense datasets, often fail to generalize well to sparse scenarios, resulting in overfitting and poor novel view generation. Addressing this challenge requires incorporating strong priors to guide the optimization process and compensate for missing data. Researchers have explored various priors, including semantic, depth, and recently, diffusion priors, to improve reconstruction quality under sparsity. Diffusion models offer a powerful approach, providing visual supervision directly through the learned score function, but their effectiveness in sparse scenarios can be limited. The low information entropy in sparse views compared to rich textual descriptions used in many diffusion model applications can lead to mode collapse or deviation, hindering successful optimization. Key research focuses on overcoming these challenges by rectifying the rendered image distribution, effectively leveraging the visual guidance offered by diffusion models while mitigating the detrimental impact of limited data and inherent ambiguities in sparse views.
Diffusion Prior Use#
The effective use of diffusion priors in scenarios with sparse views presents a significant challenge. Existing methods often struggle due to the low information entropy inherent in sparse data, leading to optimization difficulties and suboptimal results. The core problem lies in the mode-seeking behavior of score distillation sampling (SDS), which tends to deviate from the true target mode. The proposed solution, Inline Prior Guided Score Matching (IPSM), addresses this by incorporating visual inline priors derived from pose relationships between viewpoints. IPSM rectifies the rendered image distribution, improving guidance and mitigating mode deviation. The method cleverly decomposes the optimization objective, providing more effective diffusion-based guidance without requiring fine-tuning or pre-training, showcasing a significant improvement in reconstruction quality compared to existing methods.
IPSM Algorithmic Details#
An ‘IPSM Algorithmic Details’ section would delve into the inner workings of the Inline Prior Guided Score Matching method. It would likely begin by formally defining the loss function, clearly showing how it combines the original Score Distillation Sampling (SDS) loss with the novel inline prior component. The section should meticulously explain the process of generating inline priors, detailing the image warping techniques and the rationale behind using them. A crucial aspect would be a precise explanation of how the algorithm rectifies the rendered image distribution using pose relationships, ensuring that the mode-seeking behavior of SDS is effectively guided towards the correct mode. The implementation of depth and geometry consistency regularization should be described with formulas and a clear explanation of their purpose in refining the reconstructed image quality. Efficient computational strategies employed, such as any optimization techniques to improve processing speed, should also be discussed. Finally, it’s vital to explain how the algorithm uses the rectified distribution as an intermediate state to guide the overall optimization process, highlighting the interplay between visual inline priors and the diffusion prior.
SDS Limitations#
The core limitation of Score Distillation Sampling (SDS) in sparse-view 3D reconstruction is its inability to effectively leverage visual information from the diffusion prior due to the low information entropy inherent in sparse views. Unlike text prompts, sparse views contain implicit visual cues within the scene geometry and inter-viewpoint relationships. SDS fails to effectively utilize these inline priors, leading to optimization challenges and suboptimal reconstruction quality. This mode deviation problem arises because the optimization objective of SDS seeks to align the rendered image distribution with the target mode in the diffusion prior; however, the rendered distribution under sparse views often deviates significantly, causing the model to converge to an incorrect mode. Incorporating inline priors to rectify the rendered image distribution and decompose the optimization objective of SDS is crucial for overcoming these limitations and unlocking the full potential of diffusion models in sparse view synthesis.
Future Research#
Future research directions stemming from this paper could explore several avenues. Extending the method to handle more complex scenes with greater variations in viewpoint and lighting conditions is crucial for broader applicability. The current approach relies on a specific 3D representation (3D Gaussian Splatting); investigating the effectiveness of IPSM with other 3D representations would demonstrate its generalizability. A deeper dive into the theoretical underpinnings of the mode-seeking behavior in sparse-view scenarios could offer valuable insights. This could involve developing a more robust mathematical framework for understanding the optimization challenges and potentially lead to more effective solutions. Finally, integrating other types of priors, such as semantic or depth priors, in conjunction with IPSM could further enhance the quality and robustness of novel view synthesis, particularly in situations with limited available data. The integration of these different types of priors could leverage the strengths of each to overcome the limitations of using diffusion priors alone, paving the way for even more advanced solutions.
More visual insights#
More on figures

This figure compares the optimization processes of Score Distillation Sampling (SDS) and Inline Prior Guided Score Matching (IPSM). The left panel illustrates SDS, showing how the rendered image distribution (red) is drawn towards the nearest mode (red star) in the diffusion prior (blue), even if it is not the desired target mode (yellow star). This deviation leads to suboptimal results. The right panel shows IPSM, demonstrating how it rectifies the rendered image distribution (green) using inline priors, guiding the optimization towards the correct target mode (yellow star). This rectified distribution helps to suppress mode deviation and leads to improved reconstruction.

The figure illustrates the IPSM-Gaussian pipeline. It starts with sparse views and initializes 3D Gaussians. Seen views are inversely warped to generate pseudo unseen views. These pseudo views, along with depth information, are used to create inline priors. These priors modify the rendered image distribution, creating a rectified distribution. The rectified distribution then guides the optimization process using score matching, improving the final reconstruction quality. This process leverages visual knowledge from diffusion priors to improve sparse-view 3D reconstruction without the need for fine-tuning or pre-training.

This figure shows a qualitative comparison of novel view synthesis results on the LLFF dataset. The ground truth image is compared to results from 3DGS, FreeNeRF, DNGaussian, and the proposed IPSM method. Red boxes highlight regions of interest where differences are readily apparent, demonstrating the improved accuracy and detail of the IPSM results, particularly in reconstructing smaller, finer features.

This figure shows a qualitative comparison of novel view synthesis results on the LLFF dataset. It compares the ground truth images with results from three different methods: 3DGS, FreeNeRF, and DNGaussian, alongside the results from the authors’ proposed method. The visual differences highlight the relative strengths and weaknesses of each technique in terms of detail, texture, and overall reconstruction quality.

This figure illustrates the IPSM-Gaussian pipeline. It shows how seen views are inversely warped to create pseudo-unseen views. This warping, combined with depth and geometry consistency, refines the rendered image distribution, aligning it more closely with the target distribution from the diffusion model. The rectified distribution acts as an intermediate step in the optimization process, guiding the mode-seeking behavior of Score Distillation Sampling (SDS) to improve reconstruction quality. Two sub-objectives, one for rectifying and one for aligning with the diffusion prior, are used to control this optimization process.

This figure compares the optimization process of Score Distillation Sampling (SDS) and Inline Prior Guided Score Matching (IPSM). SDS, shown on the left, tends to converge to the nearest mode in the diffusion prior, leading to mode deviation and suboptimal results, especially under sparse views. The rendered image distribution (red) fails to align well with the target mode (black). In contrast, IPSM (right) rectifies the rendered image distribution (red) by leveraging inline priors, thereby guiding the optimization towards the true target mode and enhancing visual guidance.

This figure provides a visual illustration of how inline priors are used in the IPSM method. It shows a series of image transformations for several example scenes. The first column displays the ground truth image. The second shows the rendered image from a pseudo-unseen viewpoint. The third is the rendered depth for that pseudo-viewpoint. The fourth column displays the image from the seen viewpoint, warped to align with the pseudo-viewpoint. The fifth column presents a mask based on depth differences between the warped and rendered images. The sixth column shows the warped masked image, representing the inline prior. Finally, the seventh column depicts the image produced using the Stable Diffusion Inpainting model, conditioned on the noisy rendered image and the inline prior, demonstrating how the inline prior guides the mode-seeking process of the diffusion model.

The figure shows the architecture of the IPSM-Gaussian pipeline, which consists of three main components: 1) a 3D Gaussian splatting module that represents the scene using a set of Gaussian points, 2) an inverse warping module that generates pseudo views from the given sparse views, and 3) an IPSM module that leverages the inline priors obtained from the pseudo views to refine the rendered image distribution and guide the optimization process. The pipeline is designed to effectively use the visual information provided by the diffusion model without requiring fine-tuning or pre-training.

The figure shows the training process of Score Distillation Sampling (SDS) on the LLFF dataset. Three different settings are compared: Baseline (no SDS), SDS with CFG=7.5, and SDS with CFG=100. The metrics PSNR, SSIM, and LPIPS are plotted against the number of training steps. The results indicate that adding the diffusion prior (starting at 2000 iterations) significantly affects the performance, with varying results depending on the configuration (CFG). The opacity reset at step 2000 indicates a change in the training process at that point. The detailed analysis of these results is further discussed in Section 4.4 of the paper.
More on tables

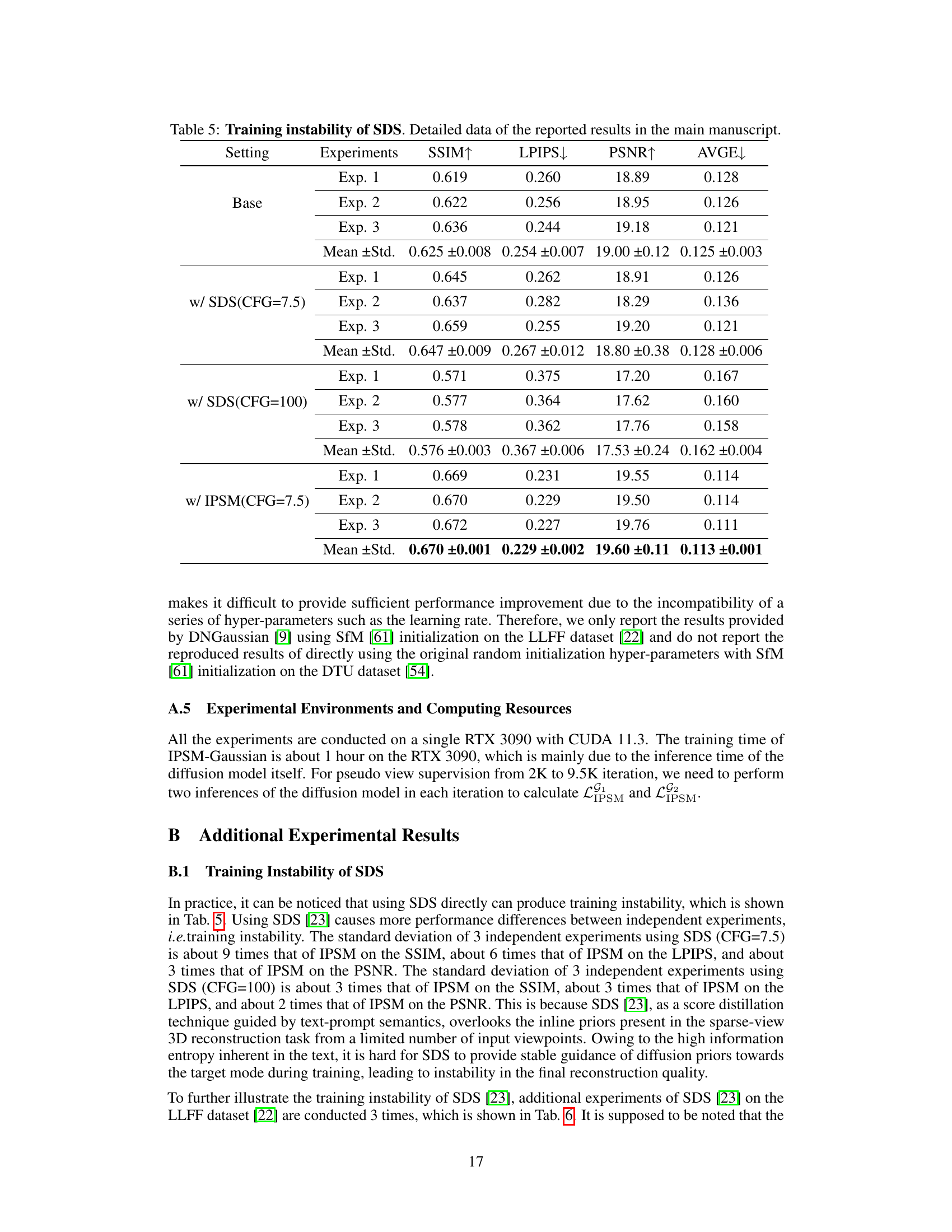
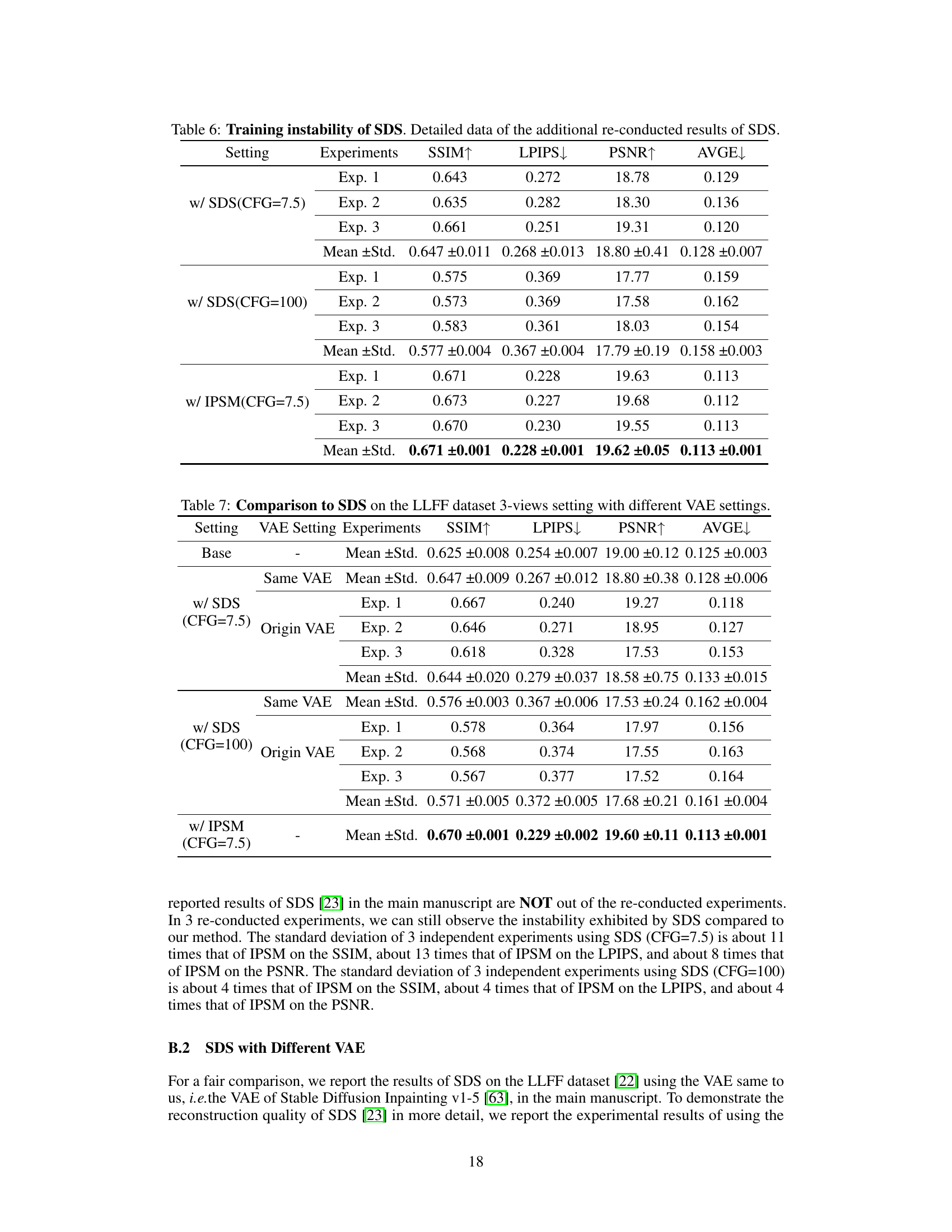
This table compares the performance of the proposed IPSM method against the baseline and two variations of Score Distillation Sampling (SDS) on the LLFF dataset using three views. The metrics used for comparison are SSIM, LPIPS, PSNR and AVGE, all common evaluation metrics for novel view synthesis. The results highlight the improved performance of IPSM compared to SDS, particularly in reducing the negative effects of mode deviation observed in SDS under sparse view conditions.

This table shows the number of total views, original training views, and test views used in the LLFF dataset for each scene. It also calculates the sparsity of using 3 views, showing the percentage of training views represented by the 3 selected views. This illustrates how the number of views used in the experiment represents a subset of the total views available, highlighting the sparsity of the data used in the paper’s experiments.

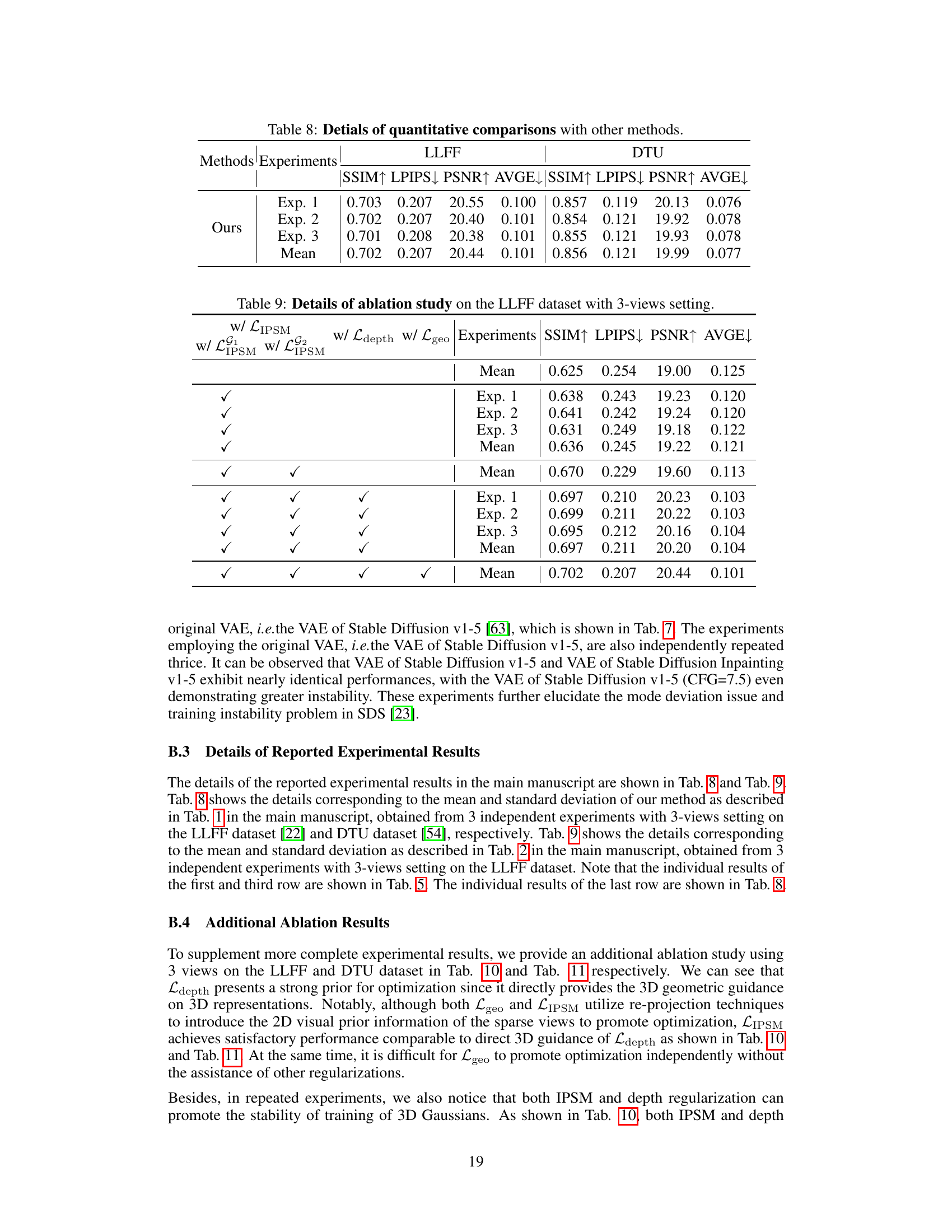
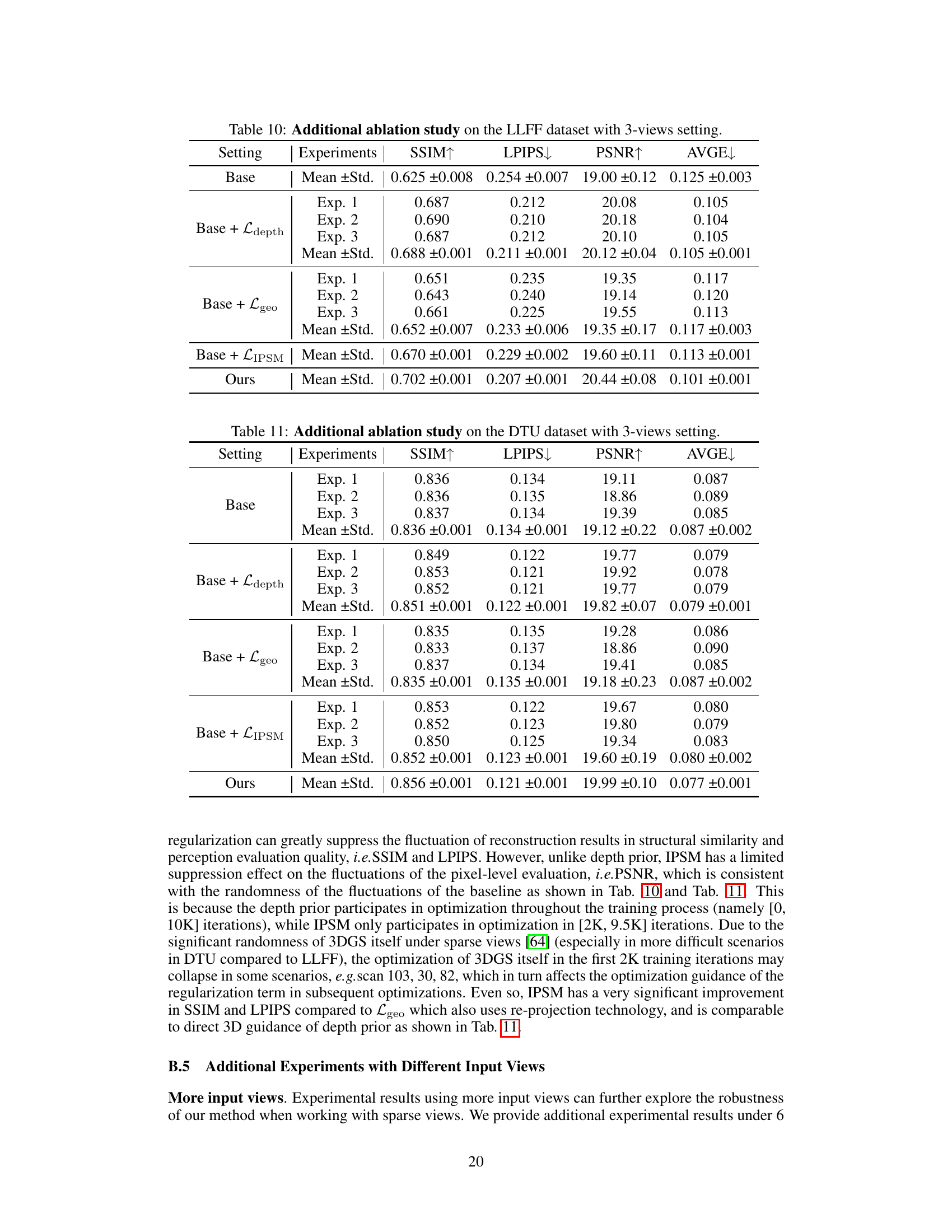
This table presents the ablation study conducted on the LLFF dataset using a 3-view setting. It demonstrates the impact of different components of the proposed IPSM method on the overall performance, showing improvements achieved by incorporating IPSM, depth regularization, and geometry consistency regularization. The metrics used for evaluation are SSIM, LPIPS, PSNR, and AVGE.

This table presents the ablation study conducted on the LLFF dataset using a 3-view setting. It shows the impact of different components of the proposed IPSM-Gaussian method on the model’s performance, as measured by SSIM, LPIPS, PSNR, and AVGE. The table compares the baseline (Base) with experiments including IPSM, depth regularization (Ldepth), geometry consistency regularization (Lgeo), and combinations thereof, to analyze the individual contributions of each component to the overall performance improvement.
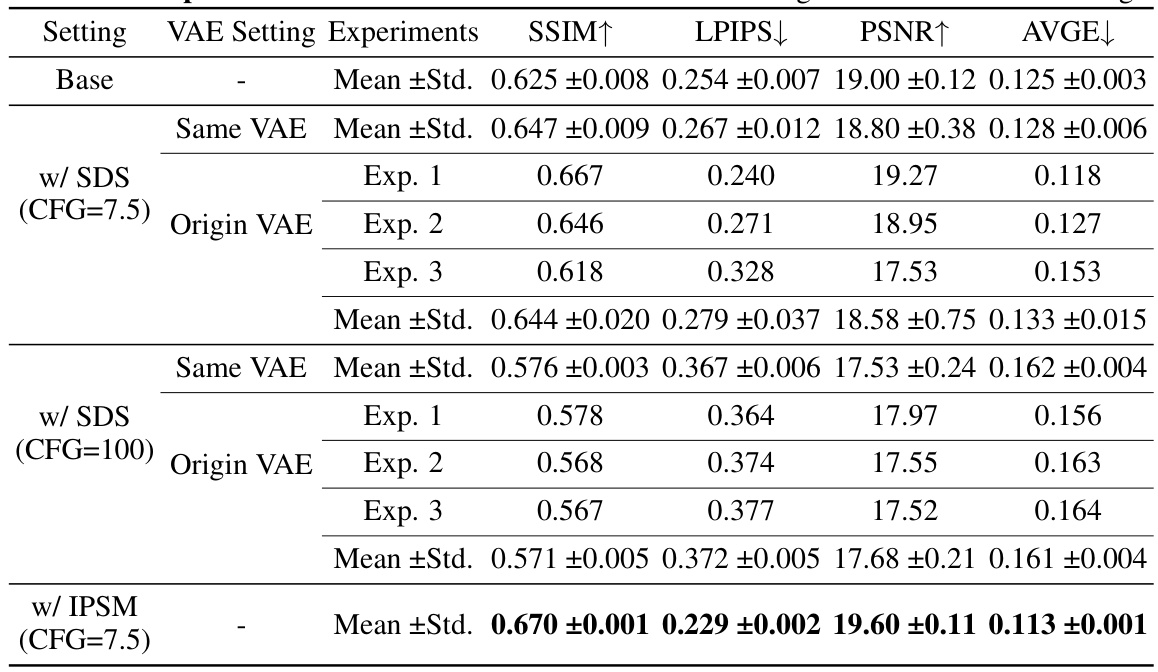
This table presents the ablation study conducted on the LLFF dataset using three input views. It shows the impact of different components of the proposed IPSM-Gaussian method on the overall performance. The metrics used are SSIM, LPIPS, PSNR, and AVGE. The rows represent different configurations, including variations of the core IPSM module, and the addition of depth and geometry consistency regularization. The results demonstrate the contributions of each component and highlight the effectiveness of the overall approach.
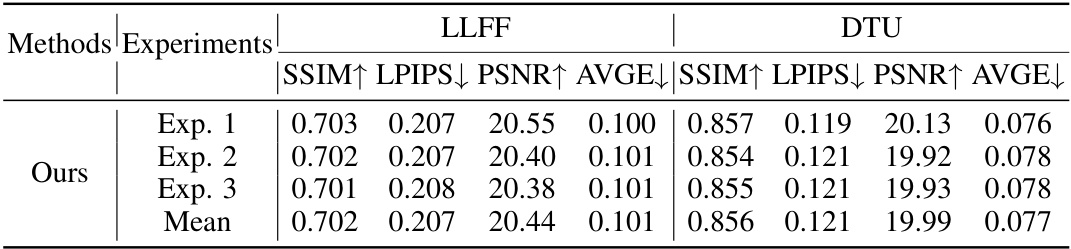
This table presents a quantitative comparison of the proposed method with other state-of-the-art novel view synthesis methods on the LLFF and DTU datasets. Metrics include SSIM, LPIPS, PSNR, and AVGE, providing a comprehensive evaluation of reconstruction quality. The results highlight the superior performance of the proposed method in various settings.
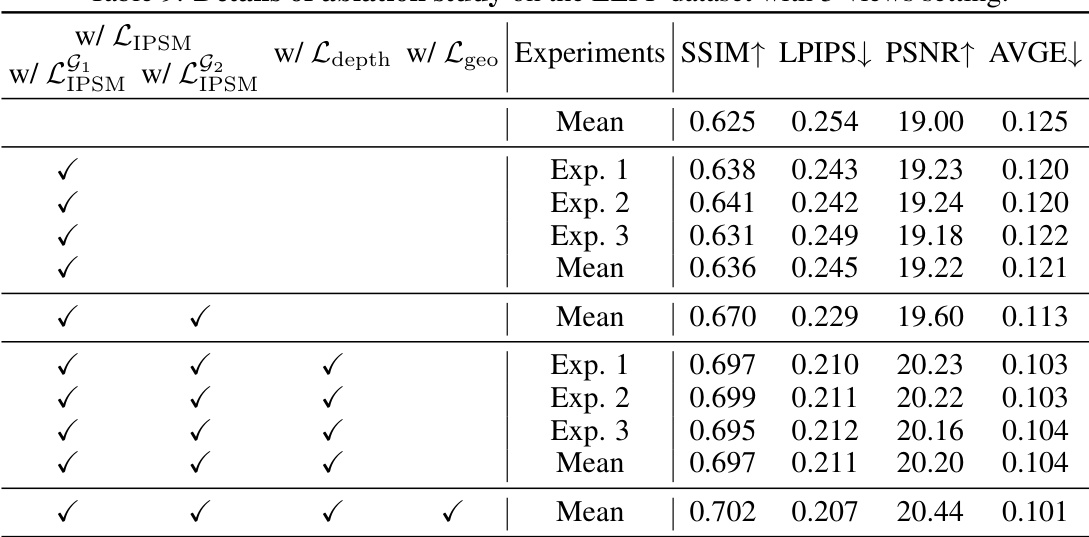
This table presents the results of an ablation study conducted on the LLFF dataset using a 3-view setting. It shows the impact of different components of the proposed IPSM method on the model’s performance, as measured by SSIM, LPIPS, PSNR, and AVGE metrics. By systematically removing components (such as LIPSM, Ldepth, Lgeo), the study isolates the contribution of each part and demonstrates the effectiveness of the proposed approach.
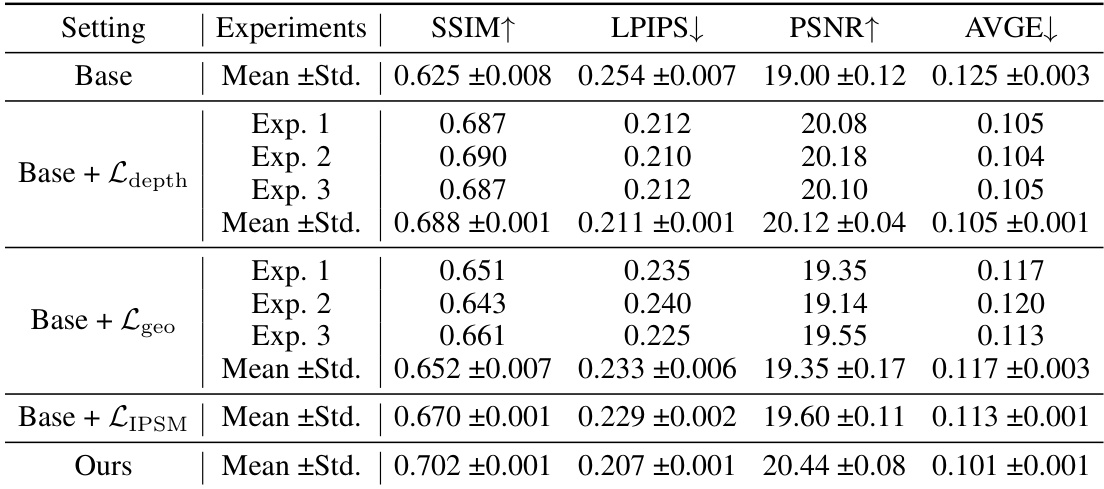
This table presents the ablation study on the LLFF dataset with 3 input views. It shows the impact of different components on the performance, namely: using Inline Prior Guided Score Matching (IPSM) alone, adding depth regularization, adding geometry consistency regularization, and combining IPSM with both depth and geometry regularizations. The metrics used for evaluation are SSIM, LPIPS, PSNR, and AVGE. The results demonstrate the individual and cumulative contributions of each component to the overall improvement in reconstruction quality.

This table presents the results of an ablation study conducted on the LLFF dataset using a 3-view setting. The study systematically evaluates the impact of different components of the proposed IPSM method on the model’s performance. Metrics such as SSIM, LPIPS, PSNR, and AVGE are used to assess the quality of the 3D reconstruction. By comparing the results with and without different components (LIPSM, depth regularization, geometry consistency regularization), the table helps to demonstrate the individual contribution and importance of each part to achieve the final results.
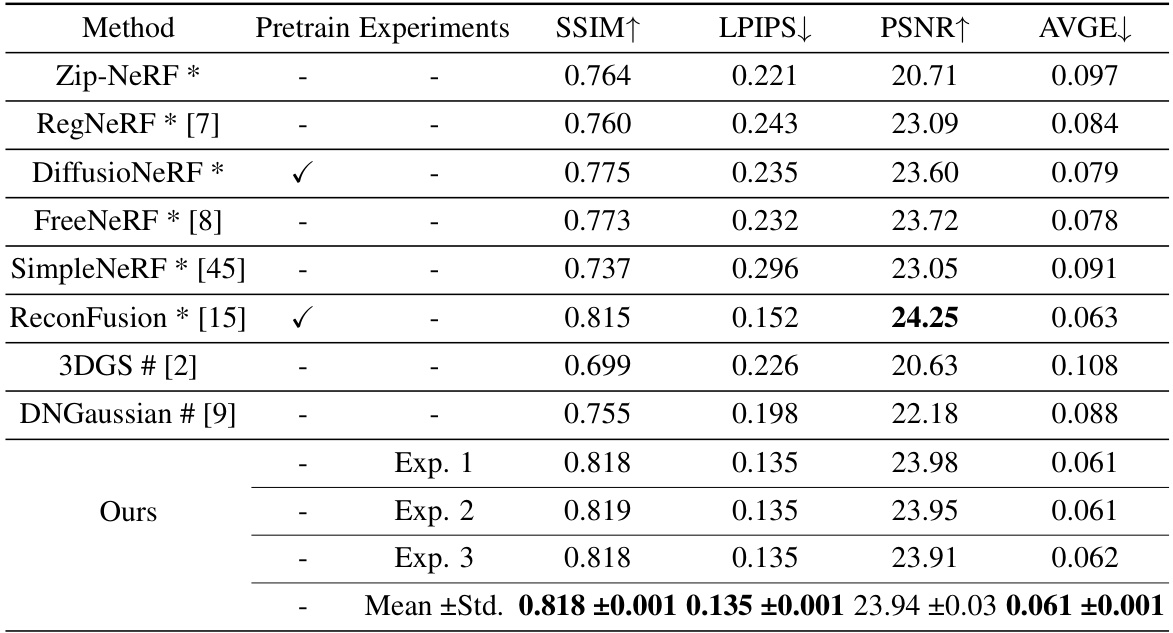
This table presents a quantitative comparison of the proposed IPSM-Gaussian method with other state-of-the-art novel view synthesis (NVS) methods on the LLFF and DTU datasets. The comparison includes metrics such as SSIM, LPIPS, PSNR, and AVGE, evaluating the reconstruction quality of each method under different settings (e.g., fine-tuning, per-scene optimization, etc.). It highlights the superior performance of IPSM-Gaussian, particularly in terms of PSNR and AVGE, indicating its improved reconstruction quality, especially when dealing with sparse views.
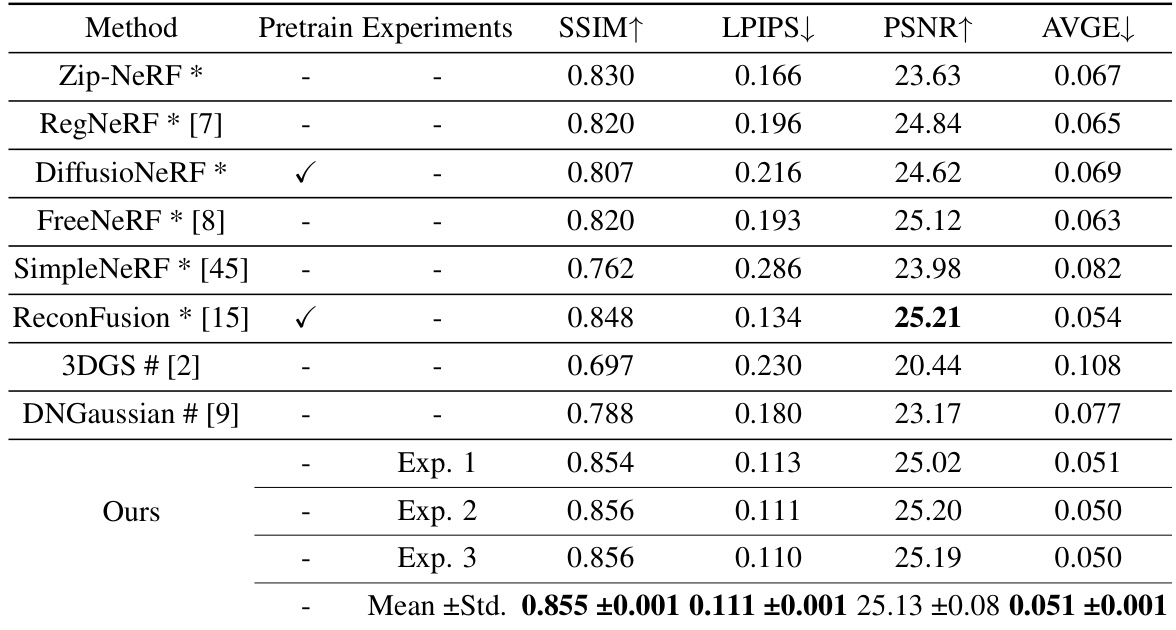
This table compares the proposed IPSM-Gaussian method to several state-of-the-art novel view synthesis methods on two benchmark datasets (LLFF and DTU). It shows a quantitative comparison using metrics such as SSIM, LPIPS, PSNR, and AVGE, which assess different aspects of image quality and reconstruction accuracy. The results highlight the superior performance of IPSM-Gaussian, especially in scenarios with sparse views.
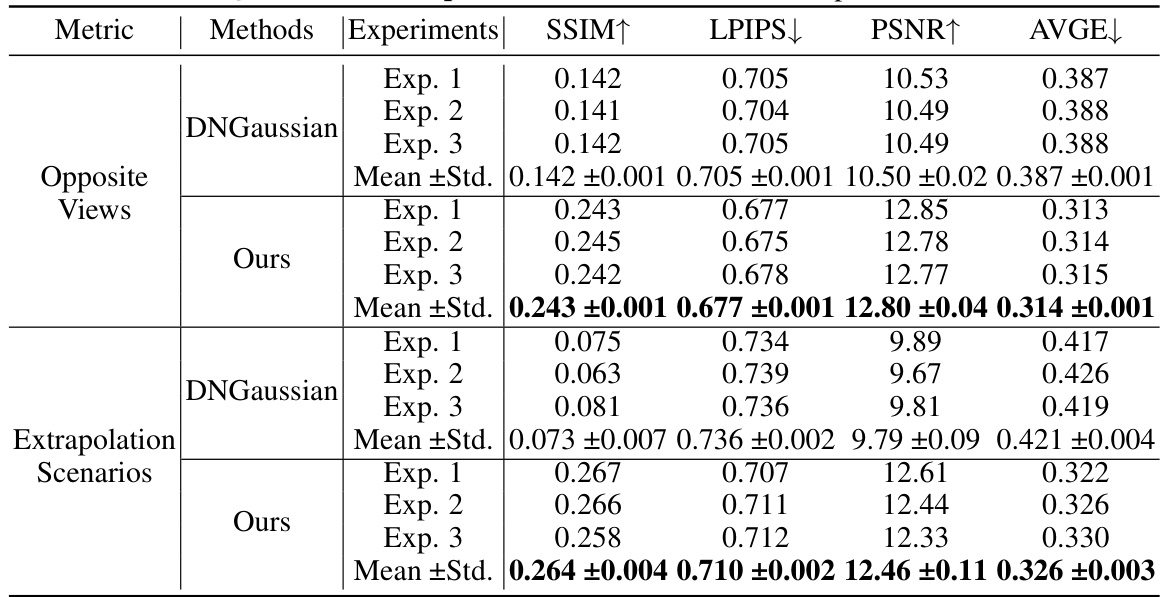
This table presents a quantitative comparison of the proposed method (Ours) with several state-of-the-art methods for novel view synthesis on the LLFF and DTU datasets. Metrics used for comparison include SSIM, LPIPS, PSNR, and AVGE. The table showcases the performance of different methods under various settings, highlighting the advantages and disadvantages of each approach in terms of image quality and reconstruction accuracy.

This table presents a quantitative comparison of the proposed IPSM-Gaussian method with other state-of-the-art novel view synthesis methods on the LLFF and DTU datasets. Metrics used for comparison include SSIM, LPIPS, PSNR, and AVGE, providing a comprehensive evaluation of reconstruction quality. The table highlights the superior performance of IPSM-Gaussian across various metrics and datasets, showcasing its effectiveness in sparse view 3D reconstruction.
Full paper#