Revisiting Self-Supervised Heterogeneous Graph Learning from Spectral Clustering Perspective

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in graph learning because it provides a novel theoretical framework for self-supervised heterogeneous graph learning (SHGL), bridging the gap between existing SHGL methods and spectral clustering. This clarifies the underlying mechanisms of SHGL and opens avenues for developing more efficient and effective SHGL techniques. It also offers enhanced generalization ability, a critical factor for real-world applications.

Visual Insights

#

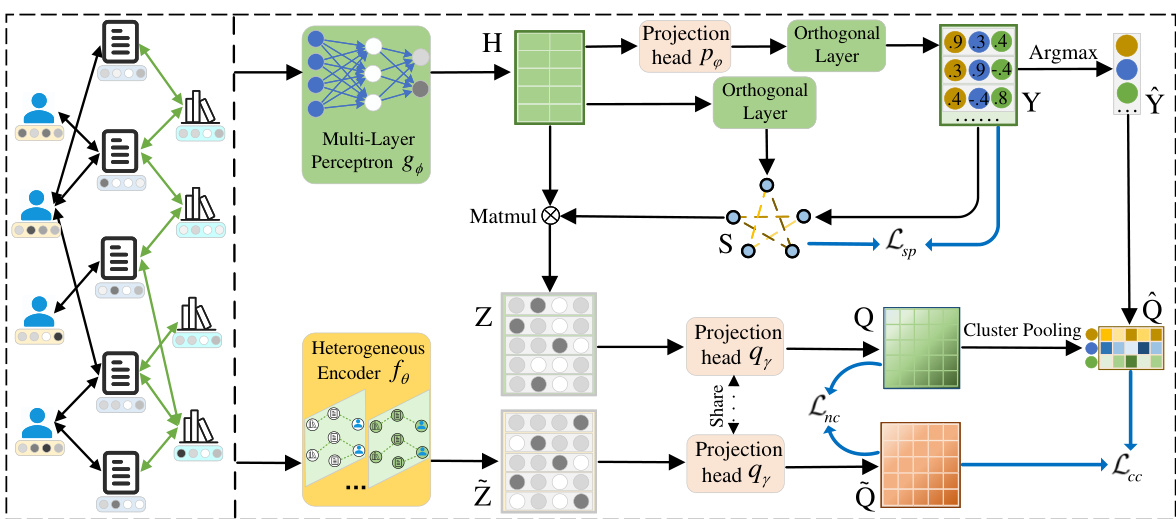
This figure shows the framework of the proposed model, SCHOOL. It illustrates the process of generating semantic representations, refining the affinity matrix to remove noise, aggregating heterogeneous information, and incorporating spectral and consistency constraints to learn effective representations.

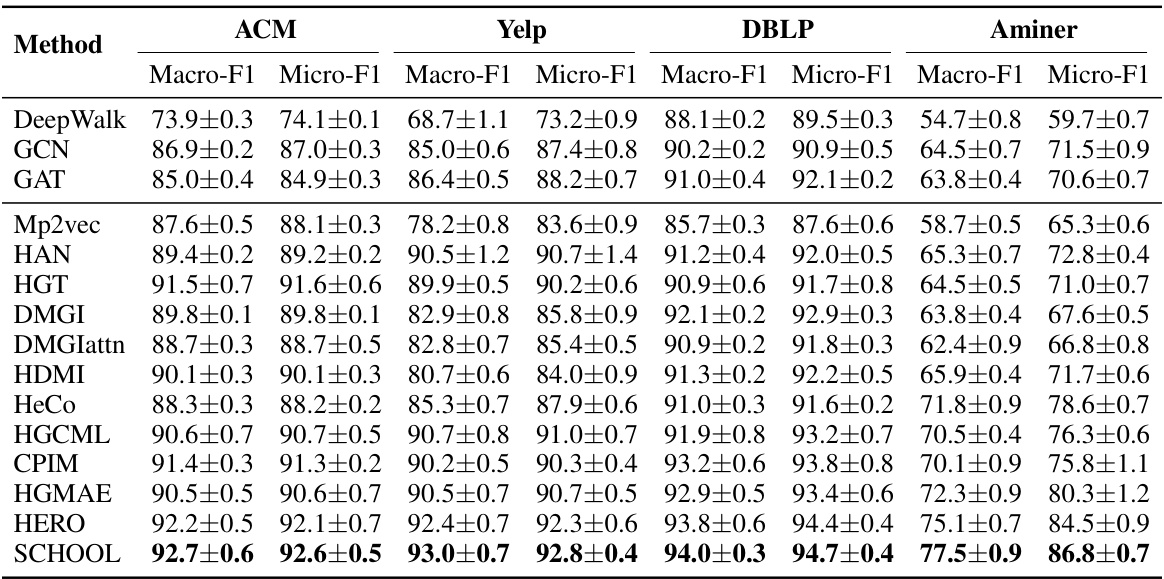
This table presents the Macro-F1 and Micro-F1 scores achieved by various methods (including the proposed SCHOOL method) on four different heterogeneous graph datasets (ACM, Yelp, DBLP, and Aminer) for a node classification task. It allows for a comparison of the performance of the proposed method against existing state-of-the-art techniques in heterogeneous graph learning.

In-depth insights

#

Spectral SHGL

#

A hypothetical ‘Spectral SHGL’ heading suggests a research direction merging spectral clustering techniques with self-supervised heterogeneous graph learning (SHGL). This approach likely leverages the strengths of spectral clustering, specifically its ability to uncover complex, non-linear cluster structures in high-dimensional data, to improve SHGL. The core idea would be to refine the graph representation or the affinity matrix used in SHGL, using spectral embedding or spectral clustering techniques. This could lead to more effective message passing and improved downstream task performance by capturing intrinsic low-dimensional structure and mitigating noise often introduced during graph construction. A key advantage could be enhanced robustness to noisy or incomplete graph data, a common challenge in real-world heterogeneous networks. The theoretical analysis of such a method might involve proving properties of the resulting embedding, such as its relationship to the true graph structure or its generalization ability. Successful application would demonstrate improved clustering, classification, and node representation learning for complex heterogeneous graphs.

Rank-Constrained Affinity

#

The concept of a ‘Rank-Constrained Affinity’ matrix in the context of self-supervised heterogeneous graph learning is a powerful innovation addressing limitations of existing methods. By constraining the rank of the affinity matrix, the approach effectively mitigates noise introduced during message-passing, leading to more reliable and discriminative node representations. This constraint ensures the affinity matrix better reflects the true underlying cluster structure of the data, reducing intra-class differences and enhancing the efficacy of downstream tasks. The core idea is to refine the affinity matrix by excluding spurious connections between nodes belonging to different classes, thus improving the quality of the resulting spectral clustering and the downstream task performance. This approach is theoretically well-founded, exhibiting enhanced generalization as demonstrated by the enhanced ability to classify nodes correctly. The rank constraint directly tackles the problem of noisy connections, a significant limitation in previous methods, offering a robust and improved approach for self-supervised heterogeneous graph learning.

Dual Consistency

#

The concept of “Dual Consistency” in the context of self-supervised heterogeneous graph learning aims to leverage both node-level and cluster-level information to enhance representation learning. Node-level consistency focuses on ensuring that different views or encodings of the same node remain consistent, capturing invariant features. Cluster-level consistency, however, ensures consistency at the cluster level; representations of nodes within the same cluster should be similar. Combining these two levels of consistency improves the quality of learned representations, leading to better downstream task performance. This approach is particularly valuable in heterogeneous graphs because of their inherent complexity and noise. The dual consistency constraints work synergistically, with node-level consistency ensuring individual node fidelity, while cluster-level consistency ensures the overall structure and separation of clusters are well-defined. This dual approach effectively bridges the gap between individual node representations and the overall cluster structure, leading to more robust and meaningful results.

SHGL Limitations

#

Self-Supervised Heterogeneous Graph Learning (SHGL) methods, while promising, face significant limitations. Noise introduction during message passing weakens node representations, hindering downstream task performance. Existing methods often inadequately capture and leverage cluster-level information, limiting their ability to fully exploit the inherent clustering structure of the data. This results in suboptimal performance, particularly in scenarios with noisy data or complex relationships. Therefore, overcoming these limitations requires novel approaches to refine affinity matrices, filtering out noise, and effectively integrating both node-level and cluster-level information to improve the quality and generalizability of learned representations.

Future of SHGL

#

The future of Self-Supervised Heterogeneous Graph Learning (SHGL) is bright, driven by the need to handle increasingly complex and diverse data. Addressing the limitations of current methods, such as noise handling and leveraging cluster-level information, will be crucial. Future research might explore more sophisticated techniques for adaptive graph construction, moving beyond simple meta-paths or rank constraints towards dynamic graph structures that genuinely reflect data relationships. Incorporating advanced techniques from spectral clustering and other dimensionality reduction methods should improve the quality and efficiency of learned representations. Moreover, exploring the integration of SHGL with other machine learning paradigms, like reinforcement learning or causal inference, could unlock new capabilities. Developing theoretical frameworks that provide stronger guarantees on the generalization ability of SHGL models will also be paramount. Finally, the application of SHGL to novel domains, such as scientific knowledge graphs and personalized medicine, promises exciting new possibilities. The development of robust and scalable SHGL algorithms is key to realizing its full potential.

More visual insights

#

More on figures

This figure visualizes the learned affinity matrix (S) and the resulting node representations using t-distributed Stochastic Neighbor Embedding (t-SNE) for both the DBLP and Aminer datasets. The heatmaps of the affinity matrices (S) clearly show a block diagonal structure indicating that the algorithm effectively groups nodes of the same class together. The t-SNE plots further demonstrate this clustering by visualizing the low-dimensional embedding of the node representations, where nodes of the same class are positioned closer together in the embedding space. This visualization supports the claim that the method effectively learns a clustered representation of the data.

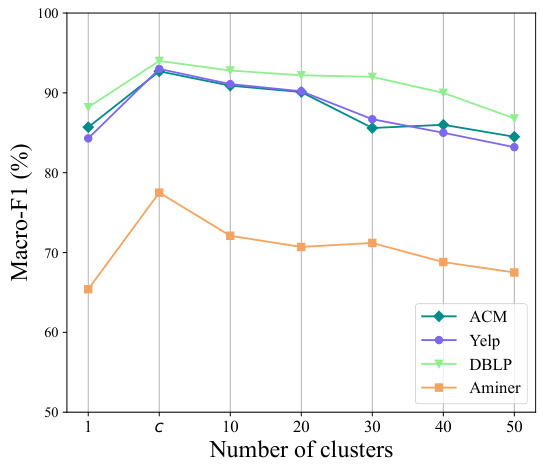
This figure shows the performance of the proposed method on node classification tasks across four different heterogeneous graph datasets (ACM, Yelp, DBLP, and Aminer) when varying the number of clusters. The x-axis represents the number of clusters, and the y-axis represents the Macro-F1 score. The results indicate that the optimal performance is achieved when the number of clusters is equal to the actual number of classes (indicated by ‘c’ on the x-axis) in each dataset. As the number of clusters deviates from the optimal value, the performance degrades.

This figure visualizes the affinity matrix S learned by the proposed method and the t-SNE representation of the node features. The visualization helps to verify the effectiveness of the proposed method in mitigating noisy connections and improving the quality of node representations. The heatmaps show the affinity matrix for DBLP and Aminer, with darker colors indicating stronger connections. The t-SNE plots show the 2-D embeddings of the node representations, demonstrating that the proposed method effectively separates nodes into distinct clusters.

More on tables

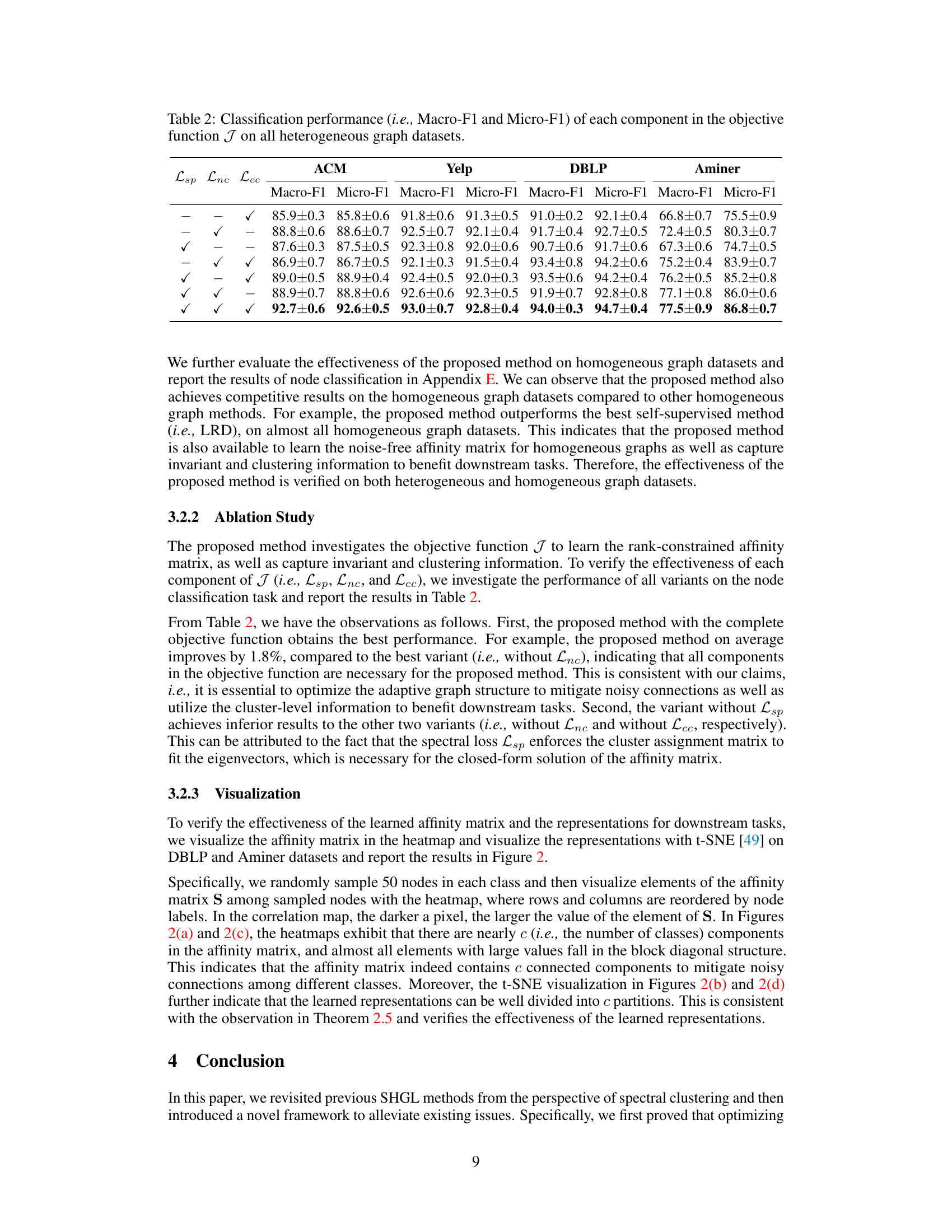
This table presents the performance of node classification using different combinations of the three components of the objective function (Lsp, Lnc, Lcc) across four heterogeneous graph datasets (ACM, Yelp, DBLP, Aminer). It shows how each component contributes to the overall performance and highlights the importance of including all three components for optimal results. The Macro-F1 and Micro-F1 scores are used as evaluation metrics.

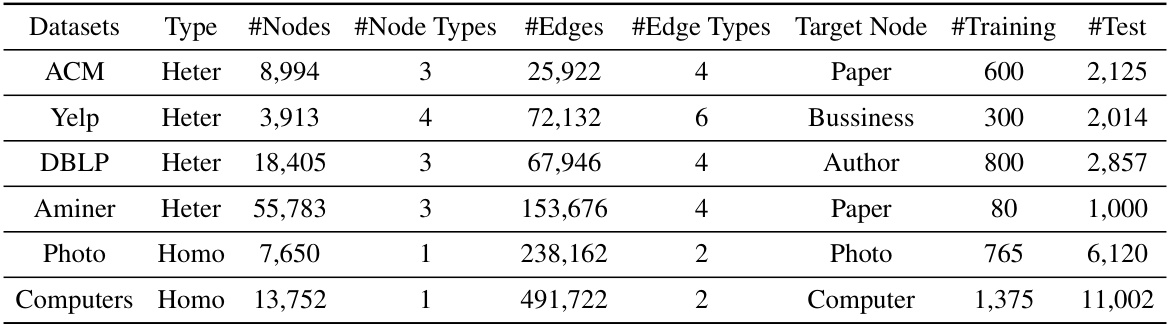
This table presents a summary of the characteristics of six datasets used in the paper’s experiments. For each dataset, it shows whether it is heterogeneous or homogeneous, the number of nodes and node types, the number of edges and edge types, the target node type for the downstream tasks, and the number of nodes used for training and testing.

This table presents the Macro-F1 and Micro-F1 scores achieved by different methods on four heterogeneous graph datasets (ACM, Yelp, DBLP, and Aminer) for a node classification task. It compares the performance of the proposed SCHOOL method against various baselines, including both traditional and self-supervised graph learning techniques. The scores indicate the accuracy of each method in classifying nodes within the heterogeneous graphs.

This table shows the hyperparameters used in the proposed SCHOOL model for different datasets. The table includes the dimension of node features (f), the dimension of the semantic representation (d1), the dimension of the projected representation (d2), and the number of classes (c) for each dataset (ACM, Yelp, DBLP, Aminer, Photo, Computers). These settings are crucial for the model’s performance and are dataset-specific.

This table presents the performance of various node clustering methods on four heterogeneous graph datasets. The performance is measured using two metrics: Normalized Mutual Information (NMI) and Adjusted Rand Index (ARI). Higher values for both metrics indicate better clustering performance. The table allows for a comparison of the proposed SCHOOL method against existing state-of-the-art methods in a node clustering task.

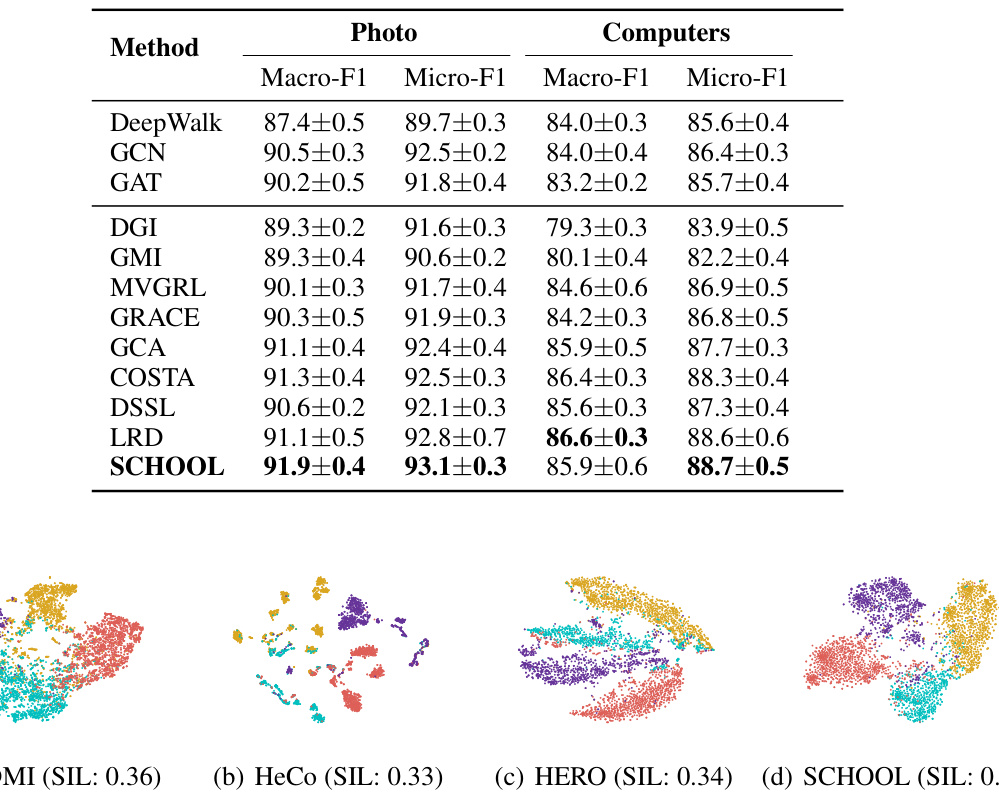
This table presents the Macro-F1 and Micro-F1 scores achieved by different methods on two homogeneous graph datasets (Photo and Computers) for node classification. The results show the performance of various methods, including DeepWalk, GCN, GAT, and several self-supervised methods, along with the proposed SCHOOL method. Macro-F1 and Micro-F1 are metrics evaluating the model’s classification performance, considering both the majority and minority classes.

This table compares the performance of three different methods for creating the affinity matrix used in the node classification task. The methods compared are using a cosine similarity matrix, a self-attention mechanism, and the rank-constrained affinity matrix proposed in the paper. The performance is measured using Macro-F1 and Micro-F1 scores across four different heterogeneous graph datasets (ACM, Yelp, DBLP, and Aminer). The results show that the proposed rank-constrained affinity matrix significantly outperforms the other two methods.

This table compares the classification performance (Macro-F1 and Micro-F1 scores) of two methods on four different heterogeneous graph datasets. The first method uses the InfoNCE loss, while the second method is the proposed approach using an affinity matrix. The results demonstrate the superior performance of the proposed method.

Full paper

#