TL;DR#
Traditional transformer networks, while powerful, suffer from interpretability issues and require extensive training data. This often results in large, complex models that are resource-intensive and may struggle with shifts in data distribution. This paper tackles these problems by proposing a novel approach based on graph signal processing. Instead of learning massive parameters, the method focuses on learning a graph structure representing the relationships between data points. This allows for far more efficient parameter learning and enhances model interpretability.
The researchers achieve this by unrolling iterative optimization algorithms that utilize learned graph smoothness priors. The core idea is that normalized graph learning is similar to self-attention, but far more efficient in terms of parameters and computation. The resulting network is significantly smaller than a comparable transformer and exhibits robust performance and a clear, mathematically-based interpretation. The experiments on image processing tasks demonstrate the method’s effectiveness and advantages, making it attractive for resource-constrained applications.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a novel approach to building interpretable and lightweight transformer-like networks by unrolling graph-based optimization algorithms. This addresses the limitations of traditional black-box transformers, which are often difficult to interpret and require large amounts of data to train. The proposed method offers improved parameter efficiency, robustness, and performance in image processing tasks, opening new avenues for research in interpretable AI and efficient neural network design.
Visual Insights#
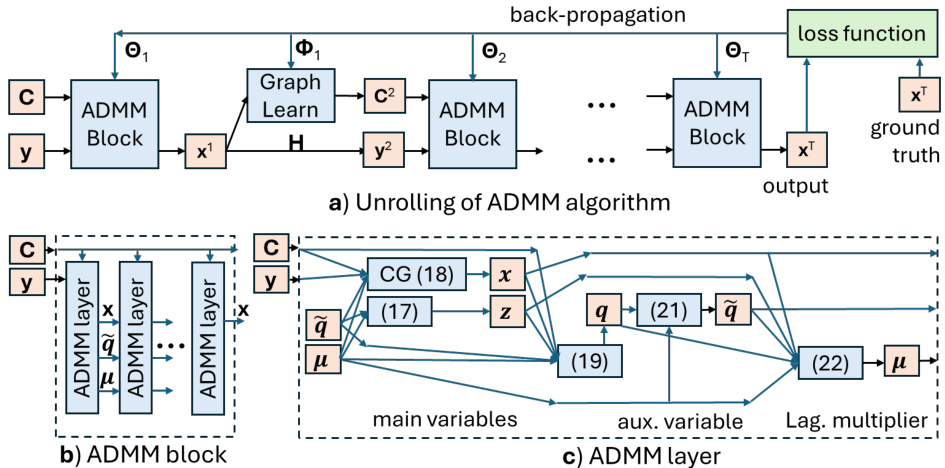
🔼 This figure illustrates the proposed deep algorithm unrolling approach. Part (a) shows the overall architecture, where multiple ADMM blocks are chained together, interspersed with graph learning modules. Each ADMM block refines the signal estimate iteratively, using a learned graph to guide the interpolation process. The graph learning modules dynamically adjust the graph structure based on the current signal estimate. Part (b) zooms into a single ADMM block and shows the internal workings of each block. The block receives an input signal and employs a conjugate gradient algorithm, (CG), to iteratively update the main variables in an alternating direction method of multipliers (ADMM) framework. Part (c) shows a single ADMM layer. The variables z, x, q, q, and μ are updated iteratively within each ADMM block using equations (17) through (22) from the paper. The process starts with a set of observed samples (y) and a learned graph, and then iterative updates yield the final interpolated signal (x*). The whole network is trained end-to-end using backpropagation.
read the caption
Figure 1: Unrolling of GTV-based signal interpolation algorithm.

🔼 This table presents the performance comparison of different image interpolation models. The models were trained using 10,000 sample image patches from the DIV2K dataset. The performance is evaluated using two metrics, Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index (SSIM), across three different benchmark datasets (McM, Kodak, and Urban100). The table includes both the number of parameters in each model and the PSNR and SSIM scores for each dataset. The results showcase the performance of the proposed graph-based models (uGLR and uGTV) in comparison to existing state-of-the-art (SOTA) models (MAIN and SwinIR-lightweight) and traditional methods (bicubic).
read the caption
Table 3: Interpolation performance for different models, trained on 10k sample dataset.
In-depth insights#
Graph Smoothness#
The concept of ‘graph smoothness’ is central to signal processing on graphs, offering a powerful framework for analyzing data residing on irregular domains. It leverages the structure of a graph to define smoothness, where signals exhibiting gradual variation across connected nodes are deemed smooth. The key idea is that smoothness is not an absolute property, but rather relative to the underlying graph structure. Different graph structures lead to different notions of smoothness and consequently impact signal processing operations such as interpolation and denoising. The choice of graph Laplacian, a fundamental matrix in graph signal processing, is crucial, as it dictates how smoothness is measured. For example, using the combinatorial graph Laplacian emphasizes differences between directly connected nodes, whereas the normalized Laplacian emphasizes relative differences, considering the degree of each node. This allows for the customization of smoothness priors to better align with the underlying data characteristics, thereby improving the interpretability and performance of the algorithms. The practical applications of graph smoothness priors extend to various fields, including image processing, where the graph encodes spatial relationships between pixels, and network analysis, where the graph represents interactions between nodes. Sophisticated techniques often involve learning the graph structure itself based on data to further enhance performance and adaptability.
Interpretable Transf.#
The heading ‘Interpretable Transf.’ likely refers to research on making transformer neural networks more interpretable. This is a significant area of study because standard transformers, while powerful, often function as “black boxes,” making it difficult to understand their decision-making processes. Research in this area might explore methods to visualize attention weights, analyze feature representations, or develop simpler, more transparent architectures that maintain performance while enhancing explainability. A key challenge is balancing interpretability with the performance gains that make transformers so attractive. Successfully achieving interpretability could lead to increased trust, improved debugging, better model design, and a wider range of applications where understanding the model’s reasoning is crucial, such as in medical diagnosis or financial modeling.
Unrolled Networks#
Unrolled networks represent a powerful paradigm shift in neural network design. Instead of relying on fixed-depth architectures, they unroll iterative optimization algorithms, treating each iteration as a layer. This approach offers several key advantages: enhanced interpretability by explicitly revealing the optimization process, improved efficiency by reducing the need for extremely deep networks, and increased robustness through a more principled approach to optimization. Each layer corresponds to an optimization step, allowing for insights into the network’s internal workings and facilitating targeted improvements. While offering these advantages, unrolling also faces limitations. The performance is highly dependent on the algorithm used. Furthermore, unrolling an excessively complex algorithm can lead to a cumbersome network design, negating the benefits of efficiency and potentially compromising stability during training. Ultimately, the success of unrolled networks hinges on carefully selecting an appropriate algorithm and architecture, striking a balance between interpretability, efficiency and performance.
Parameter Efficiency#
Parameter efficiency is a crucial aspect of machine learning, especially in resource-constrained environments. The paper investigates this by proposing lightweight transformer-like networks through the unrolling of iterative optimization algorithms. This approach reduces the number of parameters drastically, compared to conventional transformers, leading to significant computational savings. The core idea relies on using shallow CNNs to learn low-dimensional node features, which are then used to construct sparse similarity graphs. This contrasts with conventional transformers’ reliance on large key, query, and value matrices. Furthermore, the unrolled networks incorporate graph smoothness priors, simplifying the computation of the target signal. The resulting models demonstrate competitive performance with substantially fewer parameters, indicating that substantial parameter reduction is feasible without sacrificing accuracy. This strategy shows promise in applications where computational resources are limited or real-time processing is needed, highlighting the importance of algorithmic design in achieving parameter efficiency.
Future Research#
Future research directions stemming from this work could explore several promising avenues. Extending the framework to handle higher-dimensional data beyond images, such as video or 3D point clouds, is a natural next step. This would involve adapting the graph construction and learning modules to these more complex data structures. Investigating alternative graph learning approaches beyond the feature-based method used here, such as those based on spectral graph theory or autoencoders, could potentially improve the model’s efficiency and robustness. A key area for improvement lies in developing more sophisticated methods for handling covariate shift, perhaps incorporating domain adaptation techniques or adversarial training. Furthermore, analyzing the theoretical properties of the unrolled optimization algorithm with a more rigorous mathematical framework could lead to new insights and potentially more efficient implementations. Finally, applying the framework to a broader range of signal processing tasks such as denoising, super-resolution, and inpainting, would demonstrate its generalizability and practical impact. Careful investigation of these areas holds the potential to significantly enhance the capabilities and applications of this novel interpretable transformer architecture.
More visual insights#
More on figures

🔼 This figure illustrates the unrolling of the GTV-based signal interpolation algorithm. Panel (a) shows the overall architecture, depicting the sequential application of ADMM blocks and graph learning modules. Each ADMM block (b) comprises multiple ADMM layers, which iteratively update variables through conjugate gradient (CG) steps and thresholding operations, guided by a learned graph. The graph learning module (c) learns the graph structure from data by using shallow CNNs to extract features, calculate Mahalanobis distances, and create normalized edge weights, reflecting the relationships between data points. The process repeats over ‘T’ iterations to produce the final interpolated signal.
read the caption
Figure 1: Unrolling of GTV-based signal interpolation algorithm.

🔼 This figure illustrates the unrolling of the GTV-based signal interpolation algorithm. Part (a) shows the overall architecture, where multiple ADMM blocks are sequentially stacked to represent the iterative nature of the algorithm. Each ADMM block contains several ADMM layers, as detailed in part (b), which process the input signal iteratively. Part (c) shows the details of an individual ADMM layer. The graph learning module updates the graph structure at each step of the algorithm, and backpropagation optimizes the network parameters to improve performance. The whole network is built by stacking these ADMM and graph learning blocks in order to reconstruct the signal with higher precision.
read the caption
Figure 1: Unrolling of GTV-based signal interpolation algorithm.

🔼 This figure shows visual comparisons of demosaicking results for the image Urban100: image062.png. The results from the proposed methods (uGTV and uGLR) are compared to the iterative GTV method (iGTV) and the baseline methods RST-B and RST-S. The red box in the left image highlights the area being zoomed in on for the detailed comparisons.
read the caption
Figure 4: Visual demosaicking results for image Urban062.
Full paper#