↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Model-X knockoffs are powerful feature selection methods, but existing deep learning implementations struggle with the ‘swap property’, leading to reduced power. Current methods also face challenges with non-Gaussian data and small sample sizes. These limitations hinder the effective application of deep knockoffs in various fields.
DeepDRK addresses these issues by formulating knockoff generation as a multi-source adversarial problem. A novel perturbation technique further enhances the swap property, resulting in lower false discovery rates and higher power. DeepDRK outperforms existing benchmarks across diverse datasets, demonstrating its robustness and efficiency.
Key Takeaways#
Why does it matter?#
This paper is crucial because it tackles the limitations of existing deep learning-based knockoff methods for feature selection. By introducing DeepDRK, it offers a more powerful and reliable approach, particularly when dealing with small sample sizes and non-Gaussian data. This opens up new avenues for research in various fields relying on high-dimensional data analysis.
Visual Insights#

This figure illustrates the DeepDRK pipeline, a two-stage process for knockoff generation. The first stage uses a Knockoff Transformer (KT) and multiple swappers to learn a knockoff generation model while minimizing reconstructability and enforcing the swap property. This is done by optimizing a loss function that includes a swap loss (LSL) and a dependency regularization loss (LDRL). The second stage applies a Dependency Regularized Perturbation (DRP) to further refine the knockoffs, yielding XDRP. This post-processing step aims to improve the selection power of the knockoffs by reducing their dependency with the original data.
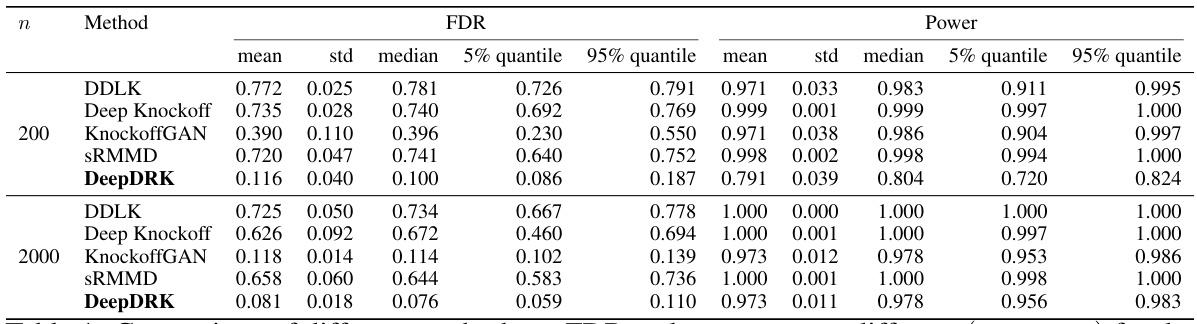
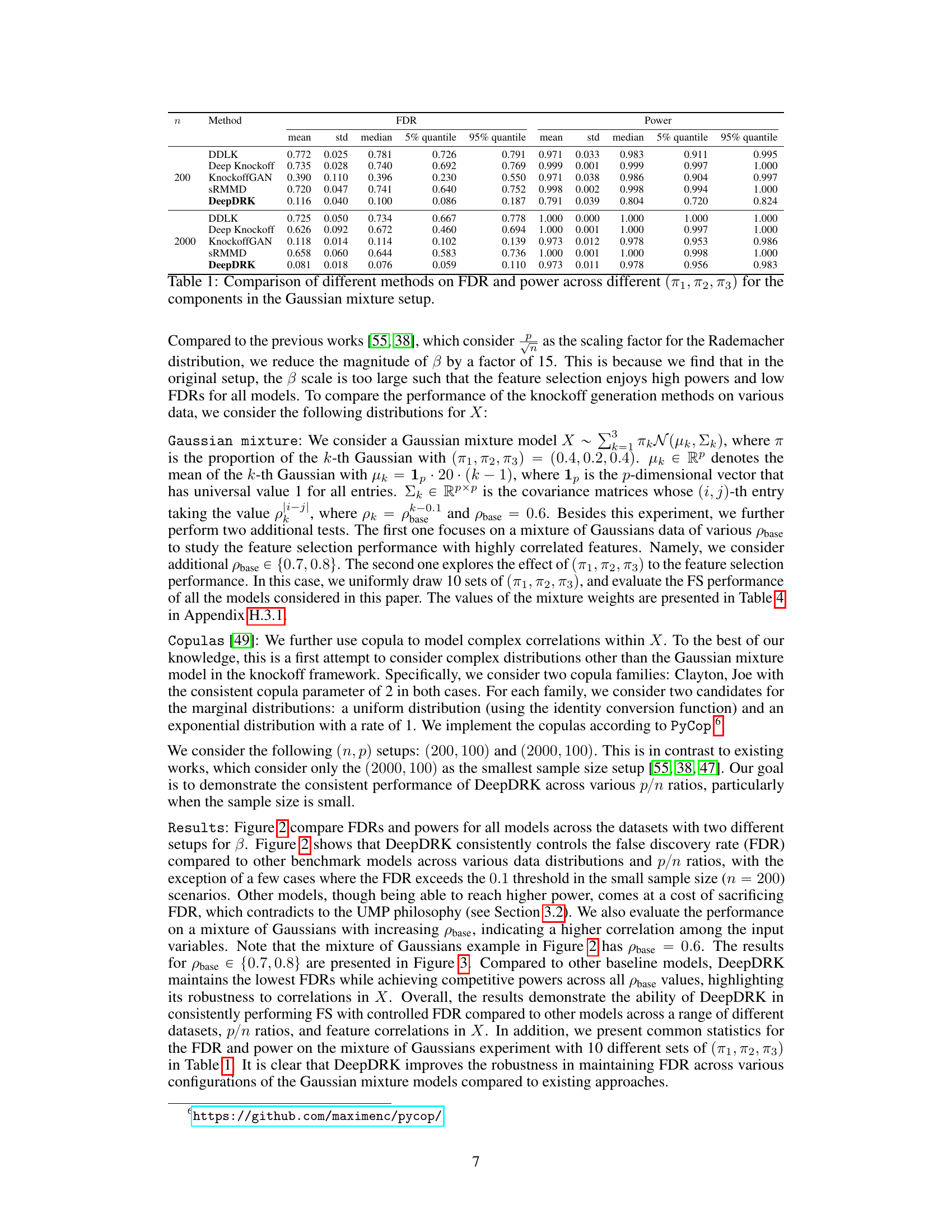
This table compares the performance of DeepDRK and other knockoff methods (DDLK, Deep Knockoff, KnockoffGAN, and sRMMD) in terms of FDR and power across different configurations of Gaussian mixture data. The configurations are defined by different proportions (π₁, π₂, π₃) of each Gaussian component. The table presents mean, standard deviation, median, 5th percentile, and 95th percentile values for both FDR and power across these configurations for sample sizes of 200 and 2000.
In-depth insights#
DeepDRK Pipeline#
The DeepDRK pipeline is a two-stage process designed for robust feature selection. The first stage involves training a Knockoff Transformer (KT) network using a novel adversarial multi-swapper approach. This cleverly addresses limitations in existing deep knockoff methods by optimizing against multiple adversarial attacks, improving the swap property at the sample level and reducing reconstructability. The second stage, a dependency-regularized perturbation (DRP), further enhances the quality of the generated knockoffs by subtly perturbing the KT output. This approach effectively balances the trade-off between false discovery rate (FDR) control and selection power, particularly beneficial for small sample sizes and non-Gaussian data. DeepDRK’s innovative combination of adversarial training and post-processing perturbation represents a significant step forward in robust and powerful feature selection.
Swap Loss Design#
The objective of a swap loss design within a knockoff-based feature selection framework is to enforce the crucial ‘swap property’. This property dictates that the joint distribution of original features and their knockoff counterparts remains invariant under the exchange of any subset of features with their corresponding knockoffs. Achieving this is vital for controlling the false discovery rate (FDR) and ensuring valid statistical inference. A well-designed swap loss should effectively guide the learning process of a deep generative model towards producing knockoffs that closely mimic the original data’s distribution, while simultaneously satisfying the swap property. The choice of loss function, its implementation, and any additional regularization techniques are all critical design considerations that directly impact the model’s ability to achieve both high power and low FDR.
DRP Perturbation#
The DeepDRK model introduces a post-training Dependency Regularized Perturbation (DRP) to further boost performance. The core idea is to address the reconstructability issue, where the generated knockoffs become overly similar to the original features, reducing the power of the feature selection. DRP adds a carefully tuned perturbation to the knockoffs, effectively decreasing the dependence between the original data and their knockoff counterparts without significantly compromising the swap property. This perturbation technique balances FDR and selection power by mitigating overfitting and enhancing the model’s robustness. The efficacy of DRP is empirically validated in the experiments, showcasing improvements across various datasets, especially in scenarios with small sample sizes and non-Gaussian distributions. The DRP stage is a crucial component in DeepDRK, improving the selection power significantly by strategically perturbing the generated knockoffs.
Synthetic Results#
A thorough analysis of synthetic results in a research paper would involve a detailed examination of the experimental setup, including the choice of data generation methods, parameter settings, and evaluation metrics. Crucially, the rationale for using synthetic data needs to be clearly articulated, addressing why synthetic data was preferred over real-world data and what specific advantages it offered for the research question at hand. The analysis would then delve into the results themselves, focusing on the statistical significance of the findings and whether they align with the expected behavior or theoretical models. Any discrepancies between observed and expected results would require careful investigation, potentially leading to the identification of limitations in the model or the experimental design. A strong emphasis should be given to the reproducibility of the results, ensuring that sufficient detail is provided for independent verification. Finally, the discussion should cover the implications of the synthetic results in the broader context of the research problem, connecting them to real-world scenarios and highlighting their potential impact.
Future Research#
Future research directions stemming from this DeepDRK model could explore algorithmic enhancements such as incorporating more sophisticated deep learning architectures or developing novel loss functions that better balance FDR control and selection power. Investigating the model’s performance on diverse data types and high-dimensional settings is crucial. Further research should also focus on theoretical guarantees, providing stronger mathematical justifications for DeepDRK’s effectiveness and robustness. Additionally, comparative studies against alternative feature selection methods, perhaps incorporating a wider range of evaluation metrics, are needed. Finally, exploring applications in real-world scenarios with challenging data characteristics or specific domain constraints would provide valuable insights into DeepDRK’s practical utility and potential limitations.
More visual insights#
More on figures

This figure compares the performance of DeepDRK and four other knockoff methods (Deep Knockoff, KnockoffGAN, SRMMD, and DDLK) on synthetic datasets where the feature coefficients are drawn from a Rademacher distribution. The figure shows the power (the proportion of true features correctly identified) and the False Discovery Rate (FDR, the proportion of incorrectly identified features among the selected features) for each method. The red horizontal line indicates a target FDR of 0.1, showing how well each method controls the FDR. The x-axis represents different synthetic datasets (Gaussian Mixture, and copulas with different marginal distributions).

This figure compares the performance of five different knockoff methods (DeepDRK, Deep Knockoff, KnockoffGAN, sRMMD, and DDLK) on synthetic datasets. The x-axis shows different data distributions (Gaussian Mixture, and four copula-based distributions) and the y-axis shows the power and FDR (False Discovery Rate). Each bar represents the average result from multiple experiments, with error bars indicating variability. The red horizontal line signifies the target FDR of 0.1. The figure demonstrates the performance of each method under various data distributions for two different sample sizes (n = 200 and n = 2000). DeepDRK generally achieves higher power while maintaining FDR below the threshold, particularly in smaller sample sizes.

The figure shows the mean and standard deviation of knockoff statistics (wj) for null and non-null features, for different knockoff methods. The results are averaged across 600 experiments with a sample size of 200. It helps to illustrate how well each method distinguishes between truly relevant (non-null) and irrelevant (null) features based on the distribution of the statistics.
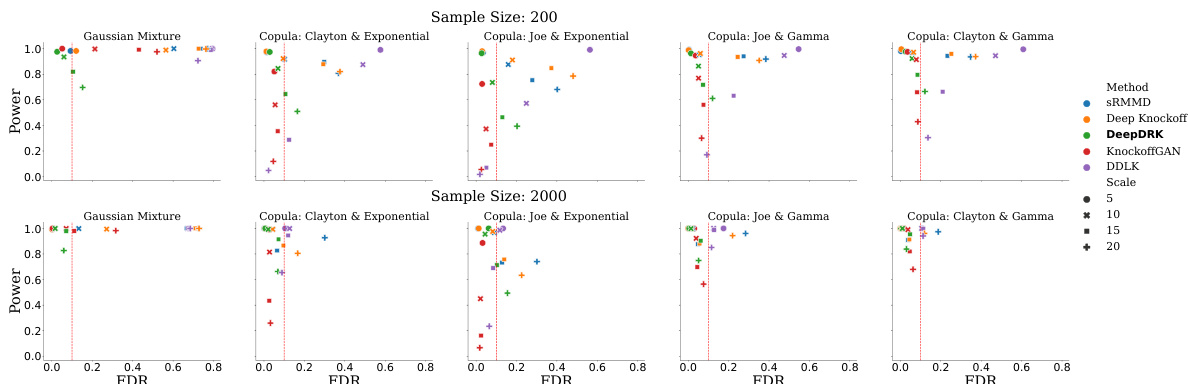
This figure compares the performance of DeepDRK and other knockoff methods in terms of power and false discovery rate (FDR) on synthetic datasets. The different colored points represent different datasets, each generated with a different copula function and marginal distribution. The x-axis represents FDR, and the y-axis represents power. The red line indicates the target FDR of 0.1. The figure demonstrates DeepDRK’s ability to maintain a low FDR while achieving higher power compared to other methods.

This figure compares the performance of DeepDRK and four other knockoff methods (Deep Knockoff, KnockoffGAN, sRMMD, and DDLK) on a semi-synthetic RNA-Seq dataset. Two different synthetic rules for generating the response variable Y are used: a linear rule and a tanh rule. The figure shows the power and false discovery rate (FDR) for each method at an FDR threshold of 0.1. DeepDRK demonstrates higher power with controlled FDR compared to the other methods, especially under the tanh rule.
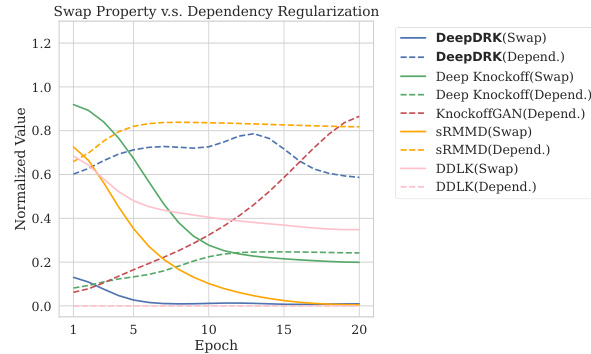
This figure shows the training curves of the swap loss (LSL) and dependency regularization loss (LDRL) for different models. It illustrates the trade-off between satisfying the swap property and minimizing reconstructability. The swap loss aims to ensure the swap property holds, while the dependency regularization loss attempts to reduce the correlation between original and knockoff data. DeepDRK demonstrates the ability to balance these losses effectively, resulting in competitive performance.
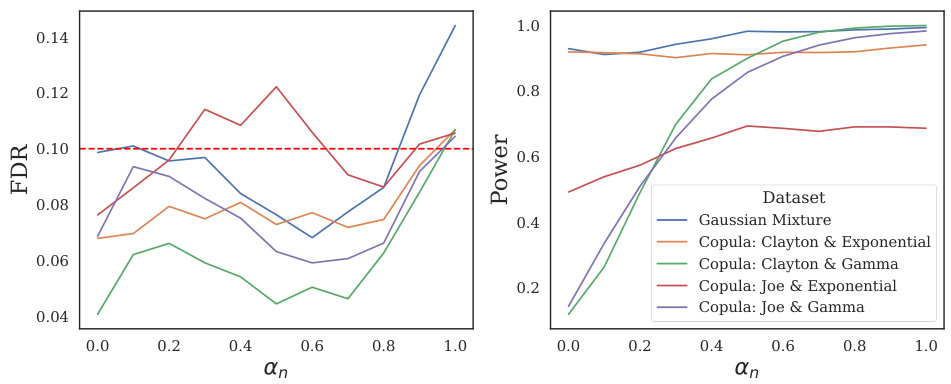
This figure shows the effect of the hyperparameter αn (perturbation weight) on the False Discovery Rate (FDR) and power of DeepDRK. The x-axis represents αn, ranging from 0 (no perturbation) to 1 (only the row-permuted version of X). The y-axis shows the FDR and power for different datasets. The figure demonstrates that an optimal value of αn balances FDR control and power, achieving a better tradeoff than using only the knockoff or only the perturbation.
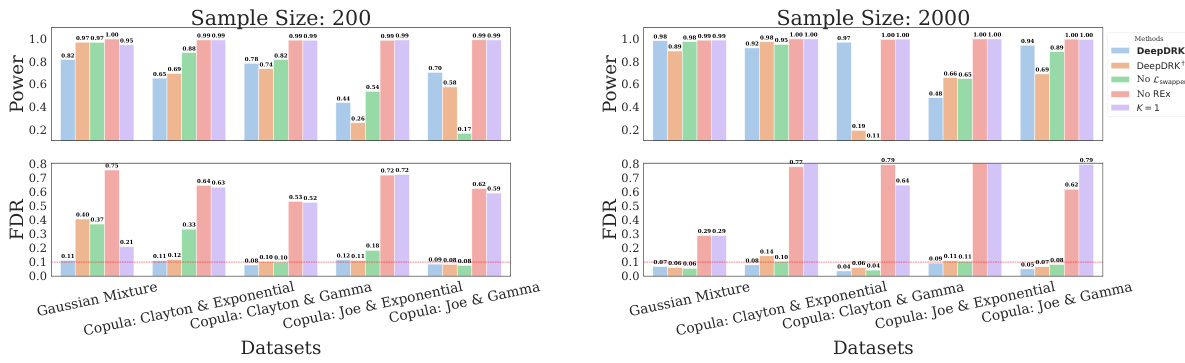
This figure presents the results of ablation studies conducted to evaluate the impact of different components of the DeepDRK model on its performance in terms of power and false discovery rate (FDR). The ablation studies remove different components of the model to isolate their effect. The results show that all components are necessary to achieve both good FDR control and high power. The red horizontal line shows the target FDR threshold of 0.1.

This figure compares the distribution of knockoff statistics (wj) for null and non-null features across five different knockoff models. The mean and standard deviation of wj are shown for each model and dataset (Gaussian Mixture, Copula: Clayton & Exponential, Copula: Clayton & Gamma, Copula: Joe & Exponential, Copula: Joe & Gamma). The sample size is 2000 and the results are averaged over 600 experiments. Ideally, a good knockoff method will have null features concentrate near zero, while non-null features have larger positive values, indicating strong separation and selection power.

This figure shows the mean and standard deviation of knockoff statistics (wj) for null and non-null features for different models on Gaussian mixture data with increased correlation (pbase = 0.7 and 0.8) and a sample size of 2000. The results show how different models handle the null and non-null features under increased correlation. DeepDRK maintains good separation between null and non-null features while other models show more overlap.

This figure displays the mean and standard deviation of knockoff statistics (wj) for null and non-null features using different feature selection models. The increased correlation in the Gaussian mixture data is a key condition for this experiment. The results show the performance of different methods under conditions of high feature correlation. DeepDRK is one of the models presented in the plot.

This figure presents the results of ablation studies on DeepDRK, investigating the impact of different components on its performance. It compares the power and false discovery rate (FDR) of DeepDRK with variations: removing the dependency regularized perturbation (DeepDRK†), removing the Lswapper term, removing the REx term, and using only a single swapper (K=1). The results are shown across five different synthetic datasets, demonstrating the importance of each component in balancing power and FDR control.

This figure presents the results of ablation studies conducted to evaluate the impact of different components of the DeepDRK model on its performance in terms of power and false discovery rate (FDR). The studies assess the effect of removing the dependency regularized perturbation, using a single swapper instead of multiple, and removing the regularization term, REx. The results are shown for two different sample sizes (n=200 and n=2000) across five different synthetic datasets, allowing for comparison under varying conditions.
More on tables

This table presents a comparison of the number of metabolites identified by different knockoff models against the number of those metabolites that have been previously reported in the literature. It provides a qualitative assessment of the accuracy of each model in feature selection, highlighting the relative proportion of true positives among the identified metabolites.

This table shows the hyperparameters used for training the DeepDRK model. It includes learning rates for the swappers and the knockoff transformer, dropout rate, batch size, regularization parameters (λ1, λ2, λ3), early stopping tolerance, and the perturbation weight (αn). These values were chosen to optimize the performance of the DeepDRK model.
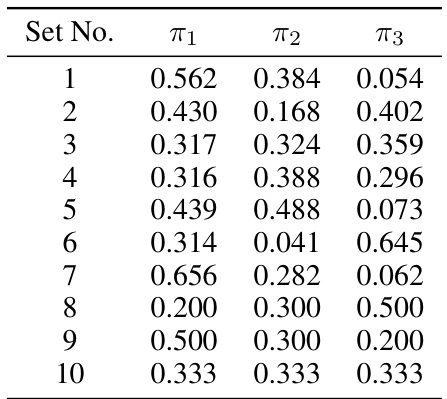
This table shows ten different sets of weights (π1, π2, π3) used in the Gaussian mixture model experiments described in the paper. These weights define the proportions of each Gaussian component in the mixture. The table is referenced in the section on synthetic experiments, where these mixture models are used to generate data for evaluating feature selection algorithms.
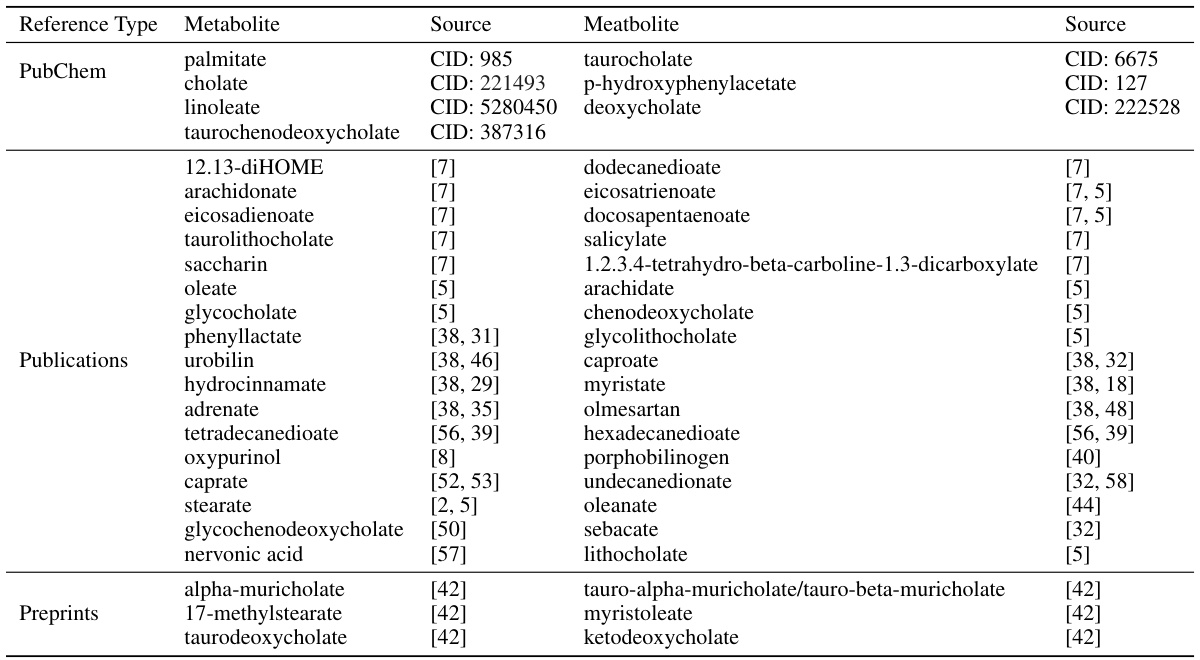
This table compares the number of metabolites identified by different knockoff models (DeepDRK, Deep Knockoff, SRMMD, KnockoffGAN, DDLK) against the number of those metabolites that have been previously reported in the literature (i.e., literature-supported metabolites). It shows how many of the identified metabolites from each model are supported by existing literature, demonstrating the ability of different models to identify previously known relevant metabolites, while controlling for false positives.
This table compares the False Discovery Rate (FDR) and statistical power of DeepDRK against other existing knockoff methods across various configurations of the Gaussian Mixture Model. The different (π₁, π₂, π₃) values represent the mixture proportions for the three Gaussian components in the model. The results highlight DeepDRK’s performance, especially in controlling FDR while maintaining high power, across different settings.
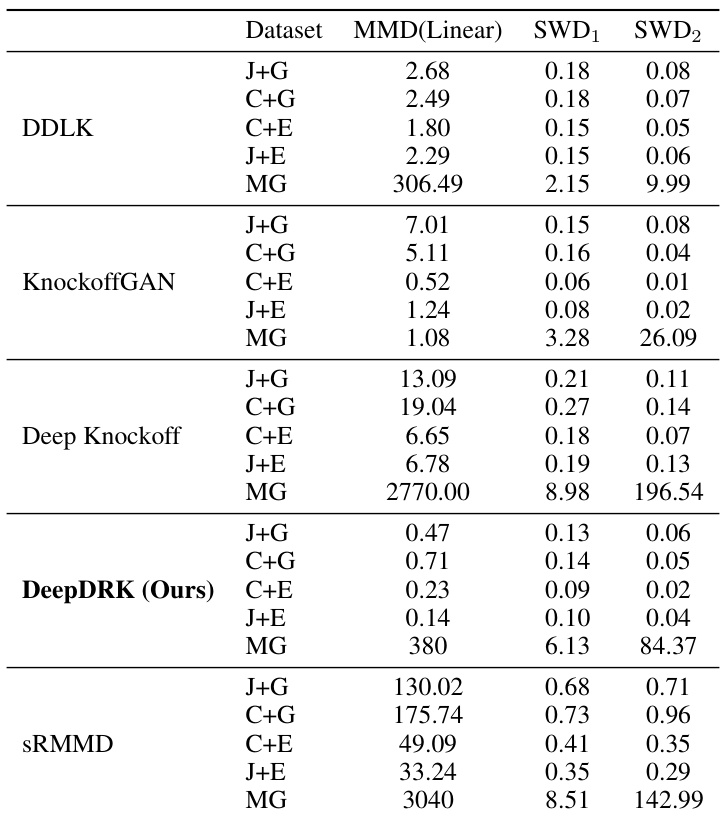
This table compares the performance of DeepDRK and several other knockoff methods in terms of FDR and power. The results are shown for different combinations of the Gaussian mixture model parameters (π1, π2, π3) and different sample sizes. The table highlights how DeepDRK achieves a balance between controlling FDR and maintaining high power, especially when compared to other methods.

This table shows the training times for different feature selection models on a dataset with 2000 samples and 100 features. The training configuration includes a batch size of 64 and 100 epochs. The models compared are DeepDRK, Deep Knockoff, sRMMD, KnockoffGAN, and DDLK. The table provides a comparison of the computational efficiency of the different models.

This table shows the number of metabolites identified by different models that were previously reported in the literature as being associated with IBD, UC, or CD. It compares the number of correctly identified metabolites (i.e., those that appear in the literature) against the total number of metabolites identified by each model. This helps to evaluate the performance of the models in selecting relevant and meaningful metabolites for IBD research.
Full paper#