S-SOS: Stochastic Sum-Of-Squares for Parametric Polynomial Optimization

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it presents a novel stochastic sum-of-squares (S-SOS) algorithm for solving parametric polynomial optimization problems. The algorithm offers quantitative convergence guarantees, which is a significant improvement over existing methods. It also introduces a new cluster basis hierarchy that improves the scalability of the algorithm, enabling it to solve larger and more complex problems. This work opens up several new avenues of investigation for researchers in global optimization, uncertainty quantification, and other areas involving polynomial optimization. The applications to sensor network localization demonstrate the algorithm’s practical effectiveness.

Visual Insights

#

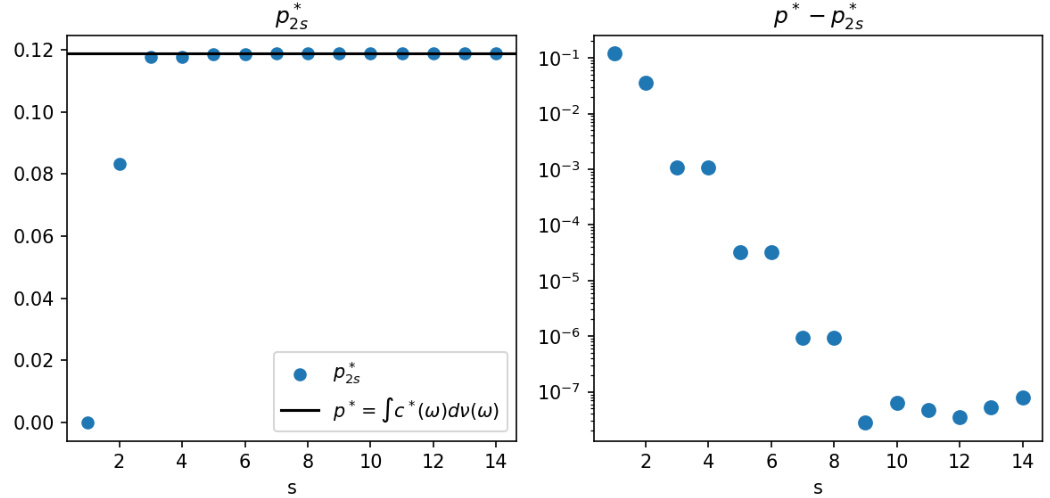
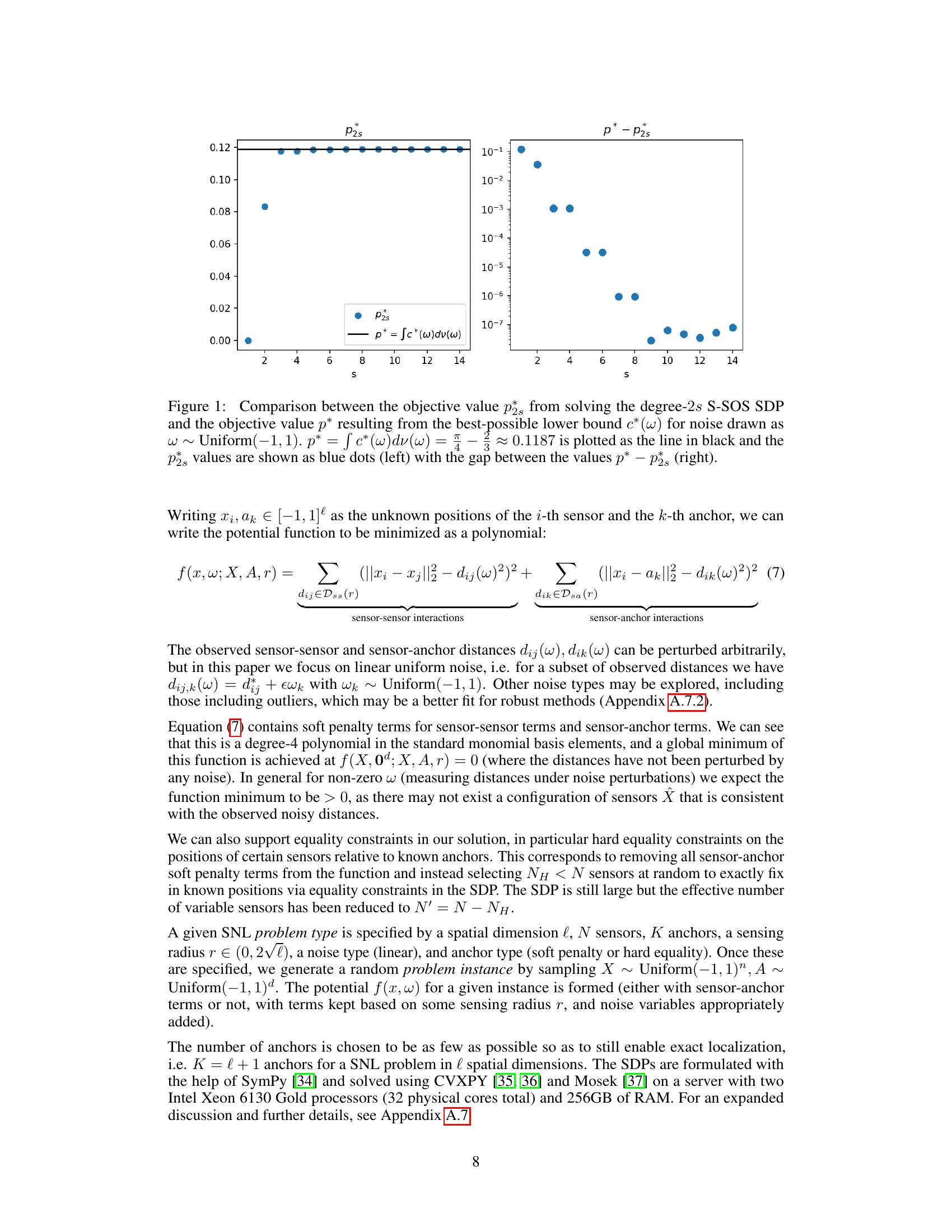
The figure shows the convergence of the S-SOS hierarchy for a simple quadratic SOS function. The left panel displays the objective values (p2s) obtained from solving the degree-2s S-SOS SDP for different degrees (s), plotted against the theoretical optimal value (p*). The right panel shows the difference (p* - p2s) highlighting the convergence rate as the degree increases.

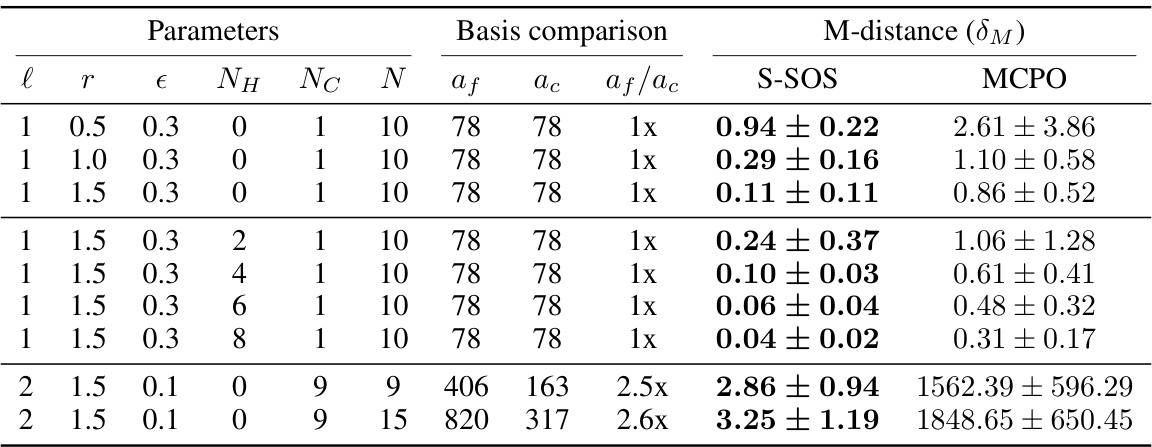
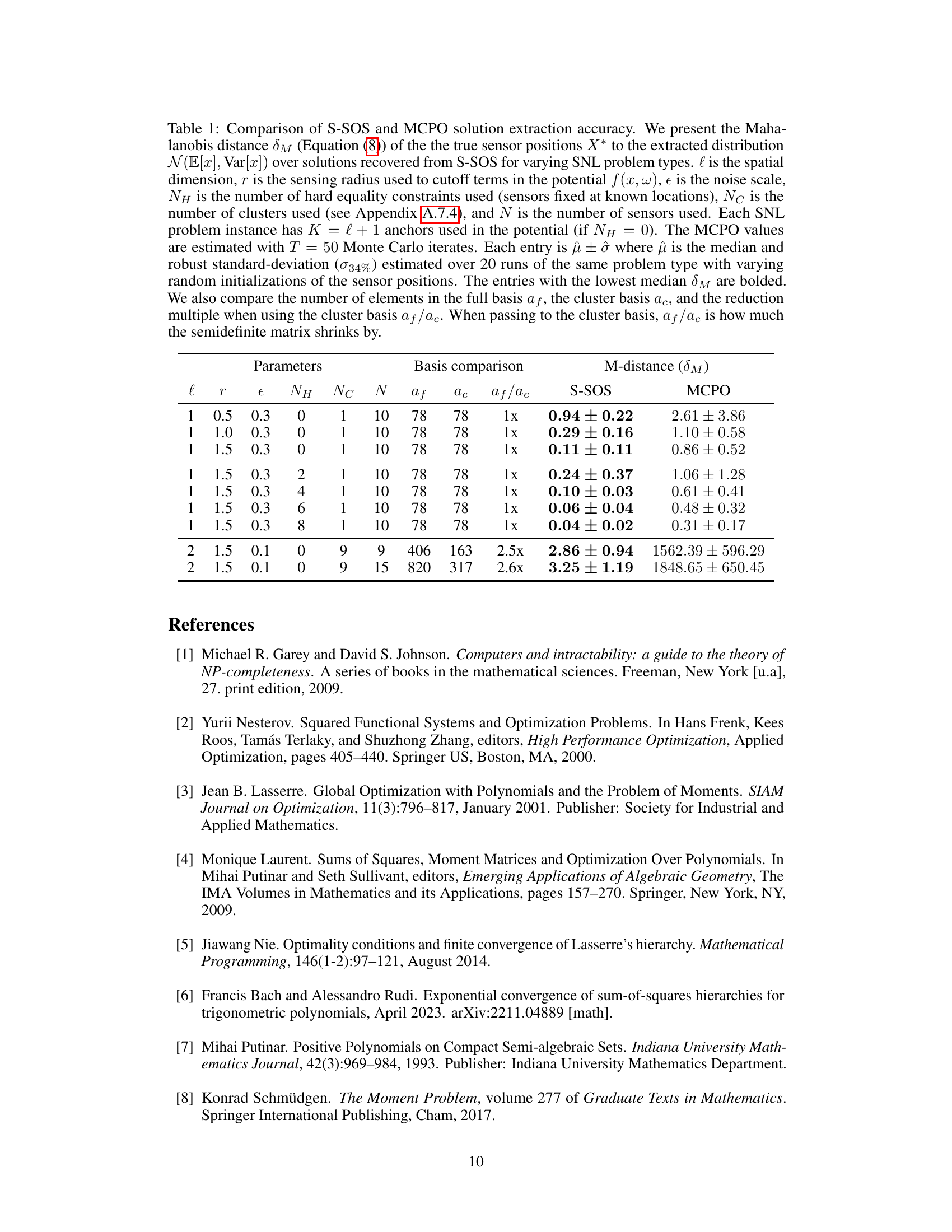
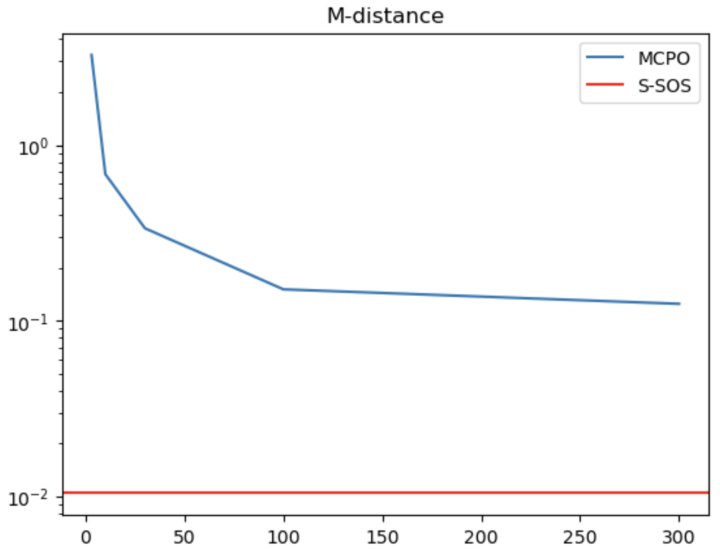
This table compares the performance of the S-SOS and MCPO methods on sensor network localization problems with varying parameters. The Mahalanobis distance is used to measure the accuracy of sensor position recovery. The table shows that S-SOS generally outperforms MCPO, especially for larger problems.

In-depth insights

#

S-SOS Hierarchy

#

The S-SOS hierarchy represents a family of semidefinite programs (SDPs) designed to tackle polynomial optimization problems with random parameters. Each level of the hierarchy refines the approximation of the global minimum by increasing the degree of the polynomials considered. This iterative process, using sum-of-squares (SOS) relaxations, systematically improves the lower bound on the global minimum. A key advantage is the ability to handle parameter uncertainty directly. Unlike Monte Carlo methods, S-SOS provides a deterministic lower bound, offering a measure of robustness. However, the computational cost increases significantly with each level, making it crucial to find balance between accuracy and feasibility. The convergence properties of S-SOS hierarchies are theoretically grounded, proving that increasing the degree guarantees convergence to the optimal solution, though the rate of convergence is a major area of research. The effectiveness of the S-SOS approach hinges on the representation power of the polynomials used and the choice of basis functions, highlighting the impact of problem structure. Sparsity-inducing techniques within the hierarchy become crucial for handling large-scale problems.

Convergence Rate

#

The research paper analyzes the convergence rate of a stochastic sum-of-squares (S-SOS) algorithm for solving parametric polynomial optimization problems. A key finding is the asymptotic convergence of the S-SOS hierarchy, meaning the algorithm’s solutions approach the true optimal solution as the degree of the polynomials increases. However, the paper establishes a convergence rate of ln s / s, where ’s’ represents the degree, which is slower than the 1/s² rate observed in standard (non-stochastic) SOS hierarchies. This slower rate is attributed to the need to approximate the optimal lower-bounding function, which is not guaranteed to be polynomial in the parametric case. The impact of different noise distributions on convergence is also explored, showing that tighter convergence is observed with narrower distributions. The paper further introduces a cluster basis hierarchy to enhance computational efficiency for large problems and suggests that this may improve the convergence rate. Overall, the convergence analysis provides valuable insights into the algorithm’s behavior, particularly highlighting the trade-off between accuracy and computational cost.

Cluster Basis

#

The concept of a ‘Cluster Basis’ in the context of polynomial optimization, particularly within the Stochastic Sum-of-Squares (S-SOS) hierarchy, presents a powerful technique for enhancing computational efficiency. By leveraging prior knowledge about the structure of the problem, specifically the presence of clusters or groups of strongly interacting variables, a cluster basis allows for sparsification of the underlying semidefinite program (SDP). This sparsification is achieved by restricting the basis functions used in the SOS representation to only include terms involving interactions within and between clusters, reducing the dimensionality of the SDP. The resulting SDP is significantly smaller and computationally less expensive to solve, thus overcoming the scaling limitations of traditional SOS methods for large problems. The cluster basis offers a practical approach to tackle large-scale polynomial optimization problems, especially those arising from applications like sensor network localization, where spatial proximity and interaction patterns are inherent. Although a full convergence proof was out of scope for the presented work, it is expected that the cluster basis hierarchy will asymptotically converge to the optimal solution, similar to traditional SOS hierarchies, offering a balance between computational feasibility and solution accuracy.

SNL Application

#

The provided text focuses on applying Stochastic Sum-of-Squares (S-SOS) to Sensor Network Localization (SNL). S-SOS offers a robust method for handling uncertainty inherent in SNL problems, where noisy distance measurements between sensors and anchors are common. The authors demonstrate that S-SOS can effectively find the global minimum of the polynomial objective function, providing accurate sensor positions and uncertainty estimates. This approach is shown to outperform a Monte Carlo method, offering significant advantages. Sparsity-inducing techniques, such as the cluster basis hierarchy, enhance the efficiency of S-SOS, making it practical for higher-dimensional problems. However, the text also acknowledges the computational limitations of SDP-based approaches for very large-scale SNL instances, suggesting further research into improved scalability is needed. The application of S-SOS to SNL is demonstrated with numerical results on various problem sizes, showcasing its effectiveness and robustness in handling noise. While promising, the scalability limitations highlight the need for further algorithmic advancements in this area.

Scalability Limits

#

The scalability of sum-of-squares (SOS) methods is often limited by the computational cost of solving large semidefinite programs (SDPs). The size of the SDP scales poorly with the number of variables and the degree of the polynomial, making it challenging to apply SOS techniques to high-dimensional problems. Sparsification techniques, such as the cluster basis hierarchy, can improve scalability by exploiting problem structure and reducing the size of the SDP. However, even with these techniques, the computational cost can become prohibitive for very large-scale problems. The choice of basis functions also greatly impacts scalability; a poorly chosen basis can lead to unnecessarily large SDPs, even with efficient sparsification. Future work should focus on developing more efficient algorithms and exploiting more sophisticated sparsity patterns to push the limits of scalability. Furthermore, investigating alternative optimization methods that are less computationally demanding than SDPs could also be beneficial.

More visual insights

#

More on figures

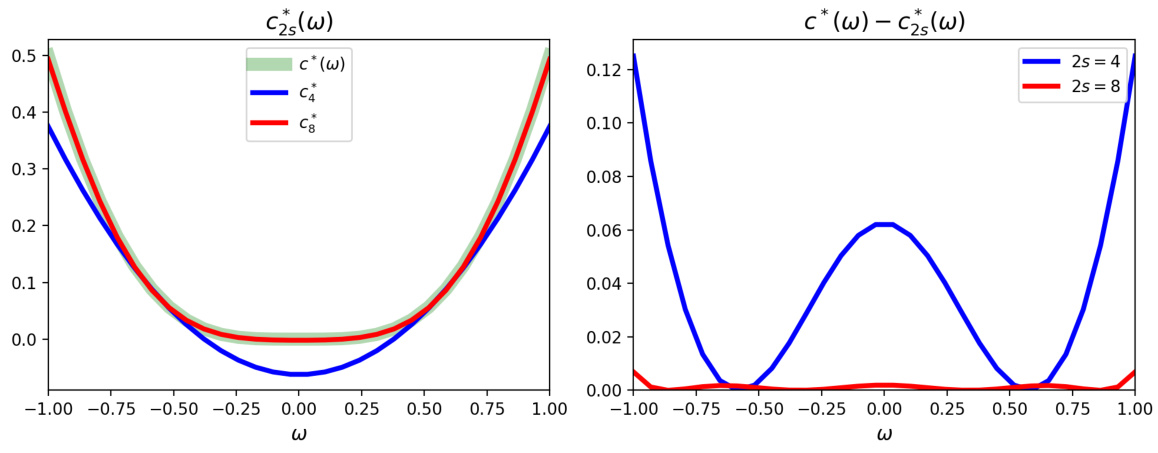
This figure shows two plots. The left plot shows the lower bound functions c* (ω) (green), c₄(ω) (blue), and c₈(ω) (red) for the simple quadratic potential f(x,ω) = (x − ω)² + (ωx)² as a function of ω. The right plot shows the difference between the true lower bound c* (ω) and the approximate lower bound functions c₄(ω) and c₈(ω) for the same simple quadratic potential. The plots illustrate how the accuracy of the approximate lower bound improves as the degree of the polynomial used to approximate c* (ω) increases from 4 (2s=4) to 8 (2s=8).

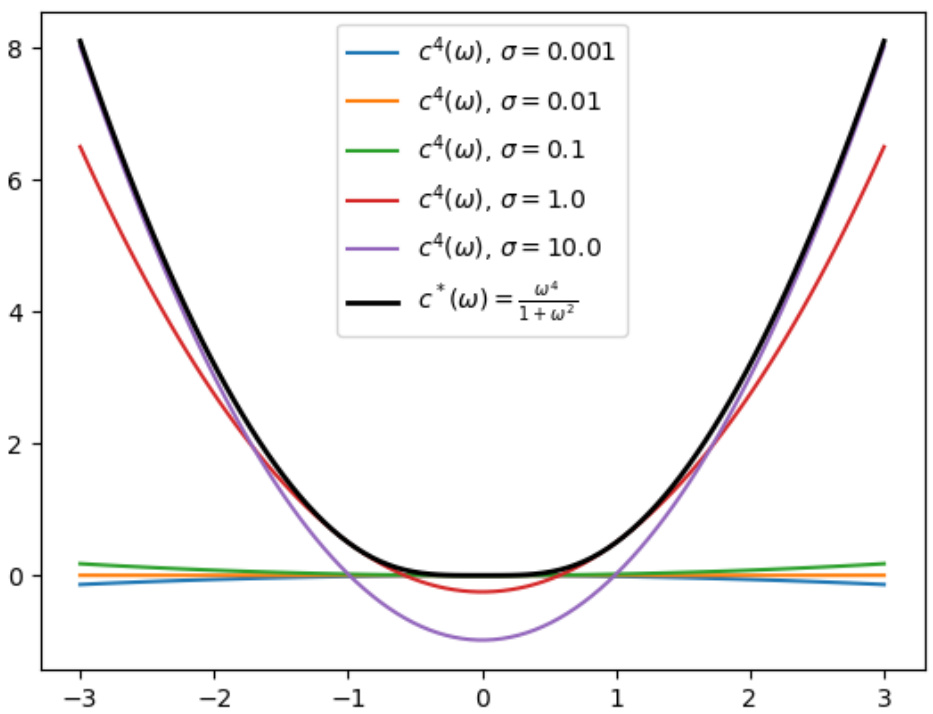
This figure shows different lower-bounding functions obtained using degree-4 stochastic sum-of-squares (S-SOS) for the simple quadratic potential f(x, w) = (x − ω)² + (wx)² with different noise standard deviations (σ). Each colored line represents a different noise level (σ = 0.001, 0.01, 0.1, 1.0, 10.0), showing how the approximation to the true lower bound (black line) changes with increasing noise. The plot illustrates the effect of noise on the accuracy of the S-SOS approximation to the optimal lower bound.

The figure shows the convergence of the S-SOS hierarchy for a simple quadratic function. The left panel shows the objective values (ps) of the degree-2s S-SOS SDP converging towards the optimal value (p*) as the degree (s) increases. The right panel shows the gap (p* - ps) between the objective values and the optimal value, demonstrating exponential convergence.

Full paper

#