↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current graph anomaly detection (GAD) methods suffer from high training costs, data requirements, and limited generalizability. They require training a separate model for each dataset, hindering their application to new domains or datasets with limited data. This is a significant limitation, especially with the growing need for flexible and adaptive anomaly detection systems.
To overcome these issues, this paper introduces ARC, a generalist GAD model that utilizes in-context learning. ARC significantly improves efficiency and generalizability by learning dataset-specific patterns from a small number of normal samples during inference, eliminating the need for retraining. The paper demonstrates ARC’s superior performance on multiple benchmark datasets from diverse domains, showcasing its ability to detect anomalies effectively and efficiently across various graph datasets without requiring dataset-specific training.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in graph anomaly detection due to its introduction of ARC, a generalist model capable of handling diverse datasets without retraining. This addresses a major limitation in current GAD methods, paving the way for more efficient and adaptable anomaly detection systems. Its in-context learning approach further enhances its practical applicability, opening avenues for research in few-shot learning and generalizable AI models for graph data.
Visual Insights#
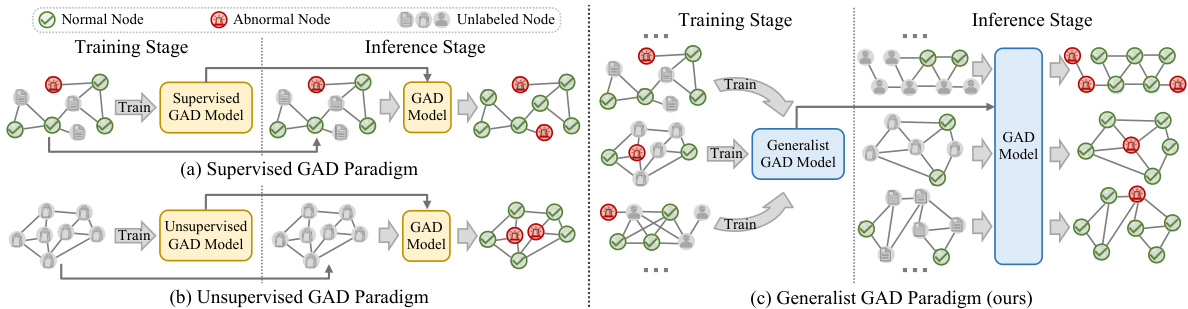
This figure illustrates three different paradigms for graph anomaly detection (GAD): supervised, unsupervised, and generalist. The supervised paradigm uses labeled data to train a specific GAD model for each dataset. The unsupervised paradigm trains a model without labels, also specific to each dataset. The generalist paradigm, which is the approach presented in this paper, trains a single model capable of detecting anomalies across various graph datasets without retraining or fine-tuning. Instead of retraining, it leverages ‘in-context learning’ at the inference stage, using a small number of normal samples from the target dataset to adapt the general model.
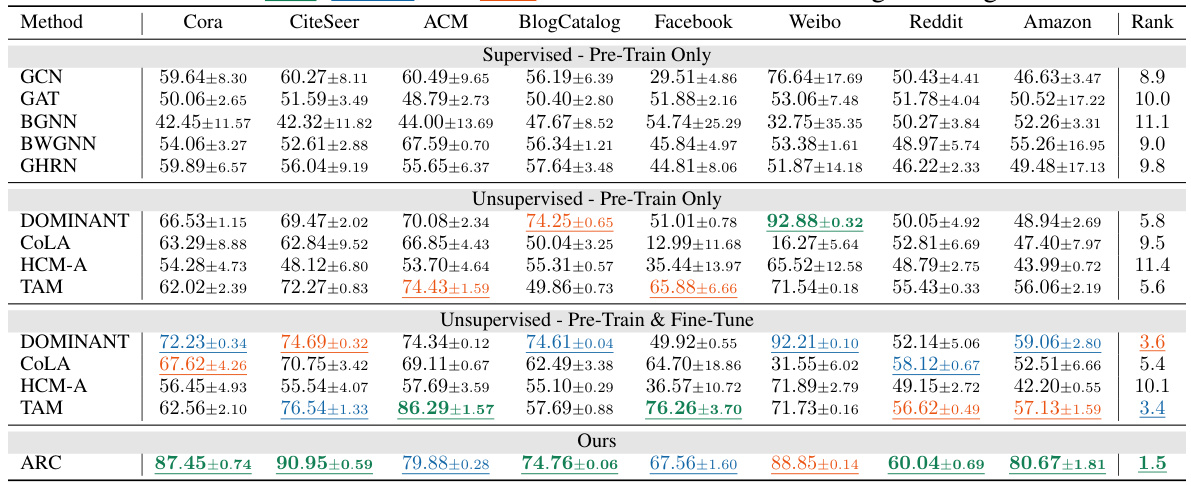
This table presents the AUROC (Area Under the Receiver Operating Characteristic curve) scores for various graph anomaly detection methods across eight benchmark datasets. The AUROC is a common metric for evaluating the performance of binary classification models, where higher values indicate better performance. The table compares supervised and unsupervised pre-trained models, both with and without fine-tuning, highlighting the performance of the proposed ARC method. The mean and standard deviation are provided for each method on each dataset. The average ranking across all datasets is also provided, offering a summary of each method’s overall performance.
In-depth insights#
Generalist GAD#
The concept of “Generalist GAD” (Graph Anomaly Detection) signifies a significant shift in the field, moving away from dataset-specific models towards universal applicability. This approach aims to create a single model capable of identifying anomalies across diverse graph datasets without retraining or fine-tuning. The key challenge lies in developing a model that can effectively extract dataset-specific patterns from limited samples during inference, while also capturing general anomaly characteristics. In essence, a generalist GAD seeks to combine the efficiency of a ‘one-size-fits-all’ approach with the accuracy of tailored solutions. This is a complex task, given the wide variability in graph structures and feature distributions across diverse domains. Successful implementation would lead to a highly efficient and adaptable system for graph anomaly detection, greatly reducing training costs and improving generalizability. In-context learning emerges as a powerful technique to achieve this objective by enabling the model to learn crucial dataset characteristics from limited samples, making generalist GAD a highly impactful research direction.
In-context Learning#
In-context learning, a key aspect of the research, is a powerful paradigm that enables a model to adapt to new tasks or datasets without explicit retraining. The study leverages this capability by enabling the model to directly extract dataset-specific patterns from a target dataset using a few-shot learning approach during the inference stage. This is particularly valuable in scenarios where retraining is computationally expensive or data is scarce, which is often the case with graph anomaly detection. The utilization of in-context learning highlights the model’s ability to generalize and adapt to various unseen graph datasets effectively, thereby enhancing its robustness and practicality. Furthermore, the in-context learning mechanism contributes to the model’s efficiency by eliminating the need for computationally intensive retraining, improving the overall performance and resource utilization.
ARC Model Details#
The hypothetical ‘ARC Model Details’ section would delve into the architecture and functionalities of the ARC model. It would likely begin by describing the three core modules: the Smoothness-Based Feature Alignment module (unifying feature representations across diverse datasets), the Ego-Neighbor Residual Graph Encoder (capturing both semantic and structural information for nodes), and the Cross-Attentive In-Context Anomaly Scoring module (leveraging few-shot normal samples for anomaly prediction). A detailed explanation of each module’s inner workings, including the specific algorithms, parameters, and layer configurations, would be crucial. Further details would include how the modules interact and the overall training process, potentially highlighting the use of in-context learning and the loss function employed. Finally, the section would likely conclude with a discussion of the model’s complexity and computational efficiency, potentially comparing it to other state-of-the-art generalist anomaly detection models.
Benchmark Results#
A dedicated ‘Benchmark Results’ section would ideally present a thorough comparison of the proposed method against existing state-of-the-art techniques. This would involve a clear articulation of the metrics used (e.g., precision, recall, F1-score, AUC), the datasets employed, and a detailed analysis of the performance differences. Visualizations like bar charts or tables showing performance across different datasets and metrics are crucial. A discussion of statistical significance testing (e.g., t-tests, ANOVA) to confirm the reliability of observed performance gains is also essential. The analysis should go beyond simple numerical comparisons and delve into the qualitative aspects of the results: Does the proposed method consistently outperform benchmarks across diverse datasets? Are there particular scenarios where it excels or underperforms? What are the tradeoffs involved in using the proposed method over existing ones (e.g., computational cost, data requirements)? Addressing these questions with a critical and data-driven approach provides compelling evidence of the method’s capabilities and limitations.
Future of GAD#
The future of Graph Anomaly Detection (GAD) hinges on addressing its current limitations and leveraging emerging technologies. Generalizability across diverse graph domains remains a key challenge, demanding the development of more robust, adaptable models that don’t require extensive retraining for each new dataset. Incorporating in-context learning techniques, like those explored in the paper, offers a promising path toward creating “one-for-all” GAD models that can quickly adapt to new datasets. Beyond this, integrating advanced graph neural network (GNN) architectures and leveraging the power of large language models (LLMs) may offer significant improvements in feature extraction, embedding generation, and anomaly scoring. Finally, exploring new evaluation metrics that go beyond the typical AUROC/AUPRC measures is necessary to better capture the nuances of GAD performance in real-world applications. Successfully addressing these challenges will lead to more practical, efficient, and scalable GAD systems with broad applicability.
More visual insights#
More on figures
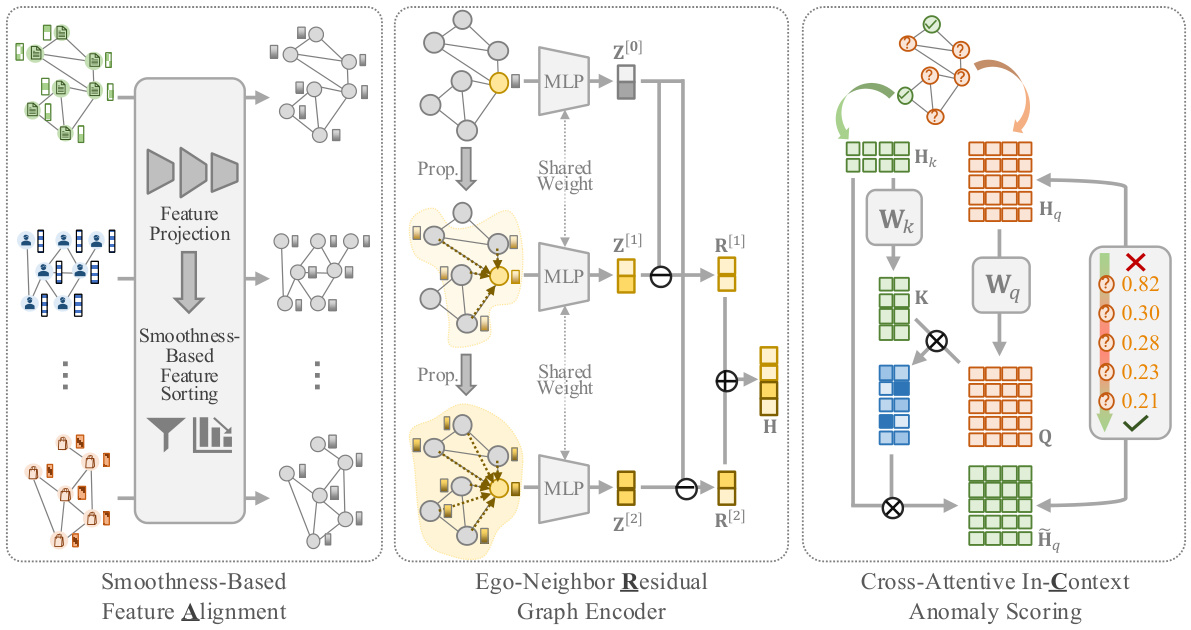
This figure shows the overall architecture of ARC, a generalist graph anomaly detection approach. It consists of three main modules: 1) Smoothness-Based Feature Alignment, which unifies features from different datasets into a common space; 2) Ego-Neighbor Residual Graph Encoder, which learns abnormality-related node embeddings using a multi-hop residual mechanism; and 3) Cross-Attentive In-Context Anomaly Scoring, which leverages few-shot normal samples to predict node abnormality using a cross-attention mechanism. The figure illustrates the flow of data through these modules and highlights the interaction between them.
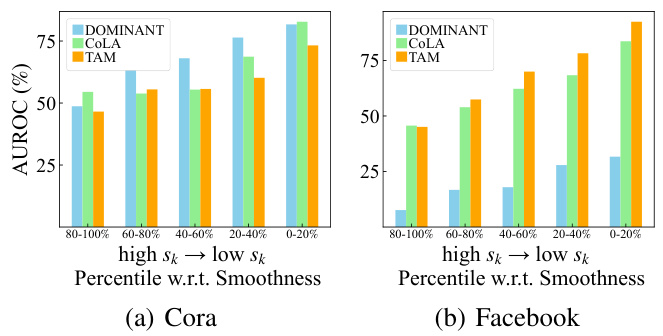
This figure displays the Area Under the Receiver Operating Characteristic curve (AUROC) results for anomaly detection experiments conducted on the Cora and Facebook datasets. The experiments involved dividing the features into five groups based on their smoothness scores (sk). Each group represents a percentile range of smoothness values (80-100%, 60-80%, 40-60%, 20-40%, 0-20%), with lower sk indicating higher frequency and heterophily, which are found to be crucial in GAD. The figure demonstrates that features with lower smoothness scores (high-frequency signals) are more effective in discriminating anomalies, indicating that smoothness serves as a robust indicator for feature selection in graph anomaly detection.

This figure shows two toy examples to illustrate how the cross-attention mechanism works in the anomaly scoring module. In Case I, there is a single class of normal nodes; their embeddings are clustered together and their reconstructed embeddings, based on the context embeddings, are also clustered near the normal nodes. The anomaly (node 5) is far from the cluster of normal nodes, and its reconstructed embedding is also distant, clearly indicating its anomalous nature. Case II shows a scenario with multiple normal classes. Again, the anomaly node 5 is easily distinguishable from the multiple normal node clusters.

This figure shows the performance of ARC with varying numbers of context nodes (nk). The x-axis represents the number of context nodes, and the y-axis represents the AUROC and AUPRC. The figure demonstrates that as the number of context nodes increases, the performance of ARC generally improves, indicating its ability to leverage information from these few-shot normal samples during inference. However, the improvement plateaus after a certain point, suggesting that adding more context nodes beyond a threshold doesn’t significantly benefit the model’s performance.

This figure compares the inference time and fine-tuning time (per epoch) for various GAD methods on the ACM dataset. It shows that ARC has comparable inference time to the fastest GNN baselines (GCN and BWGNN) and significantly outperforms the unsupervised methods. It also highlights that dataset-specific fine-tuning consumes significantly more time than inference.

The figure illustrates the architecture of ARC, a generalist graph anomaly detection model. It consists of three main modules: 1) Smoothness-Based Feature Alignment, which unifies features from different datasets; 2) Ego-Neighbor Residual Graph Encoder, which learns abnormality-related node embeddings; and 3) Cross-Attentive In-Context Anomaly Scoring, which predicts node abnormality using few-shot normal samples. The figure shows the data flow and interactions between these modules during both training and inference stages.

This figure visualizes the Area Under the Receiver Operating Characteristic (AUROC) scores obtained from experiments on two datasets, Cora and Facebook. The experiments involved dividing features into 5 groups based on their smoothness (sk), ranging from high to low. The graph illustrates the AUROC for each group of features, revealing the correlation between feature smoothness and model performance in anomaly detection. Features with lower smoothness (high-frequency graph signals) demonstrate improved AUROC scores compared to those with higher smoothness (low-frequency signals). This finding suggests that high-frequency signal features are more relevant to anomaly detection tasks.

This figure presents a visual representation of the ARC model’s architecture. ARC consists of three main modules: Smoothness-Based Feature Alignment, Ego-Neighbor Residual Graph Encoder, and Cross-Attentive In-Context Anomaly Scoring. The figure illustrates the data flow through each module, starting from the input features, and culminating in the anomaly scores for each node. It also highlights how ARC leverages few-shot normal samples during inference via in-context learning.

This figure illustrates the architecture of ARC, a generalist graph anomaly detection method. It consists of three main modules: 1) Smoothness-Based Feature Alignment, which unifies features across different datasets; 2) Ego-Neighbor Residual Graph Encoder, which learns abnormality-aware node embeddings using a residual GNN; and 3) Cross-Attentive In-Context Anomaly Scoring, which predicts node abnormality by leveraging few-shot normal samples using cross-attention. The figure shows the flow of data through each module and how they interact to achieve generalist anomaly detection.
More on tables
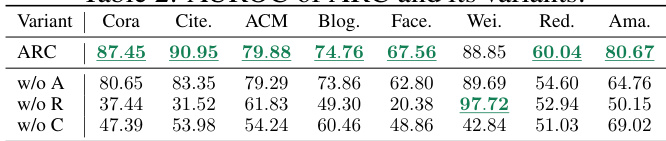
This table presents a comparison of the anomaly detection performance of different methods (including ARC and baselines) across eight datasets using the AUROC metric. The AUROC scores (Area Under the Receiver Operating Characteristic curve) represent the model’s ability to distinguish between normal and anomalous nodes. Higher AUROC scores indicate better performance. The table includes mean and standard deviation scores across multiple trials, and highlights the top three performing methods for each dataset to help make comparisons easier.

This table presents the AUROC (Area Under the Receiver Operating Characteristic curve) scores for various graph anomaly detection methods across eight datasets. The AUROC is a common metric for evaluating the performance of binary classifiers (in this case, classifying nodes as anomalous or normal). The table compares several supervised and unsupervised methods, with and without pre-training and fine-tuning. The mean and standard deviation of AUROC are reported for each method across multiple trials, providing a measure of performance stability and variability. The ‘Rank’ column gives the average rank across all datasets, helping to summarize the overall performance of each method.
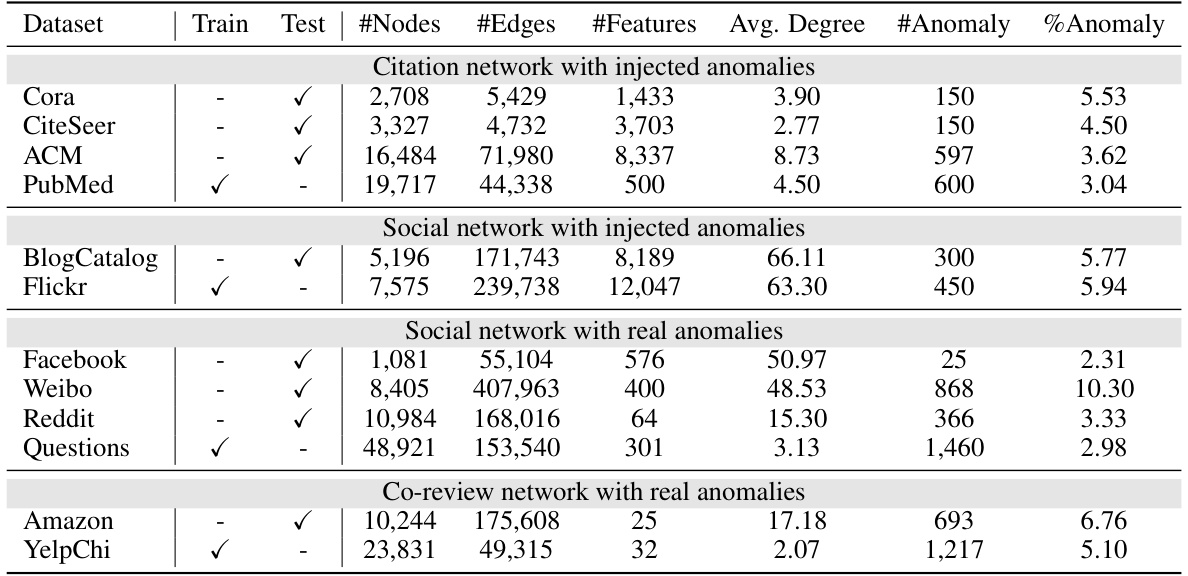
This table presents the Area Under the Receiver Operating Characteristic curve (AUROC) scores for various graph anomaly detection methods across eight datasets. The methods are categorized as supervised (with pre-training only or with pre-training and fine-tuning) and unsupervised (with pre-training only or with pre-training and fine-tuning). For each method and dataset, the mean AUROC and standard deviation are reported. The best three performing methods for each dataset are highlighted. An average ranking of the methods across all datasets is also provided.
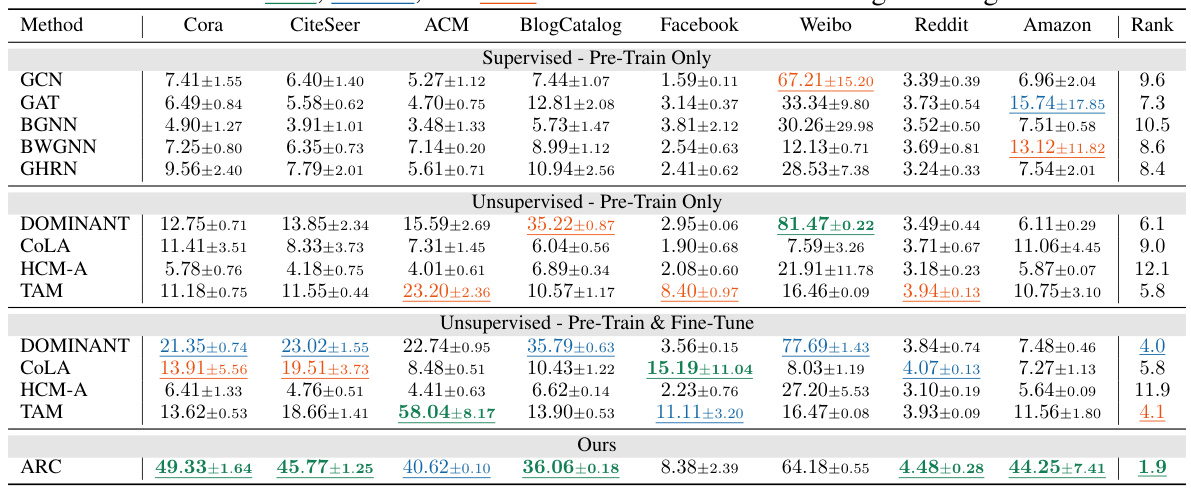
This table presents the results of anomaly detection experiments using various methods (GCN, GAT, BGNN, BWGNN, GHRN, DOMINANT, COLA, HCM-A, TAM, and ARC). The performance is measured by the Area Under the Receiver Operating Characteristic curve (AUROC), showing the mean and standard deviation across multiple trials. The table is split into supervised and unsupervised sections, further subdivided by pre-training only and pre-training and fine-tuning. The best-performing three methods for each dataset are highlighted. The ‘Rank’ column provides the average ranking of each method across all eight datasets.

This table presents the performance of various graph anomaly detection methods (including the proposed ARC method) across eight datasets in terms of Area Under the Receiver Operating Characteristic curve (AUROC). The results are presented as mean ± standard deviation (std) based on 5 trials, and the average ranking across all datasets is provided. Highlighting indicates the top three performing methods for each dataset. The methods are categorized into supervised (with pre-training and pre-training with fine-tuning) and unsupervised (with pre-training only and pre-training plus fine-tuning) groups to show the various training settings.

This table presents the AUROC (Area Under the Receiver Operating Characteristic curve) scores for various graph anomaly detection methods across eight different datasets. The AUROC metric measures the performance of a classifier. Higher AUROC indicates better performance. The table compares the performance of ARC (the proposed method) against several baselines, including both supervised and unsupervised methods with and without pre-training and fine-tuning. The mean and standard deviation of AUROC are presented for each method on each dataset. The ‘Rank’ column provides an average rank of each method across the eight datasets.
Full paper#



















