Learning via Surrogate PAC-Bayes

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers facing computational bottlenecks in optimizing PAC-Bayes bounds, particularly those working with complex models like ODEs or PDEs. It provides a novel, principled method that significantly speeds up the learning process by using surrogate objectives. This opens new avenues for applying PAC-Bayes to challenging real-world problems previously deemed computationally intractable, thus expanding the scope of PAC-Bayes applications.

Visual Insights

#

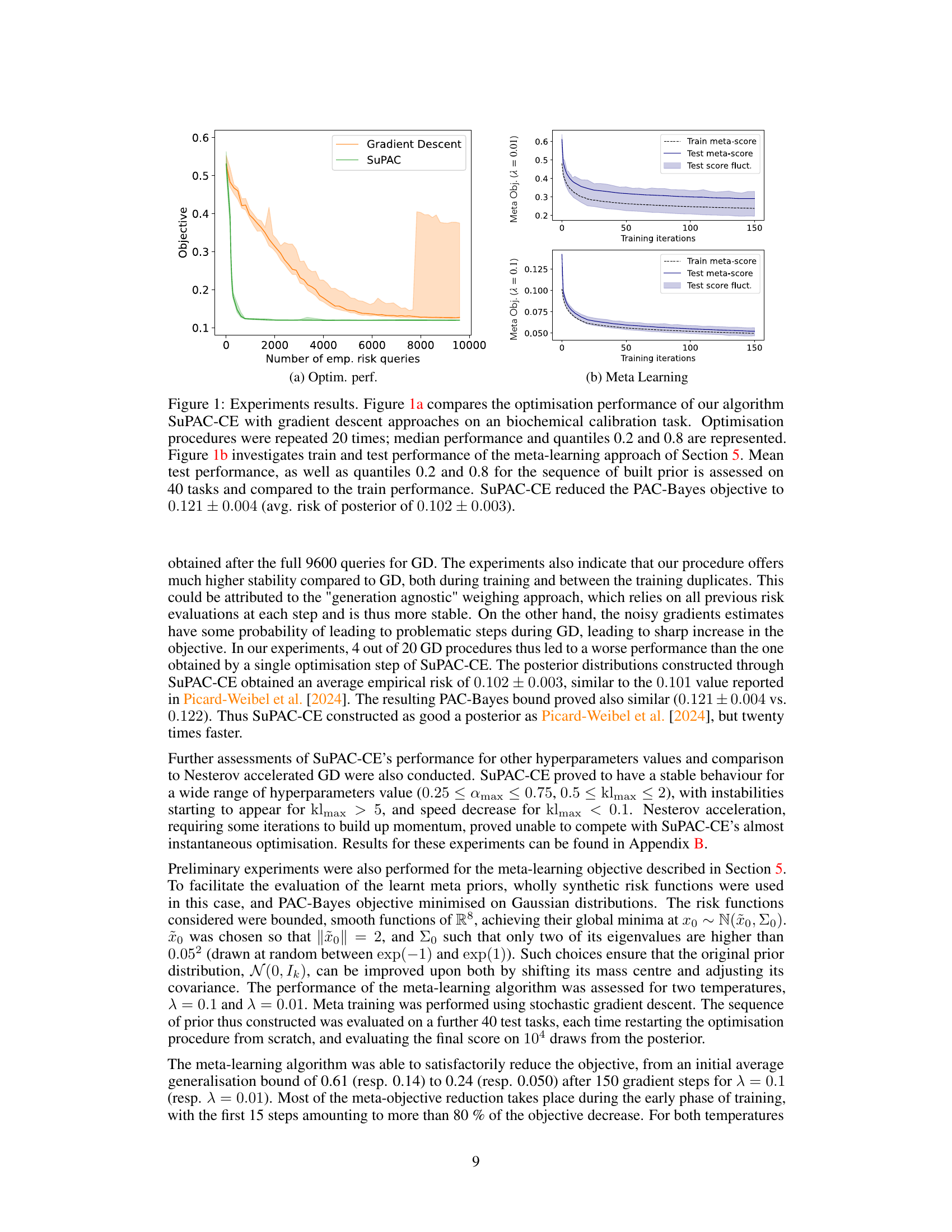
This figure summarizes the experimental results of the paper. Figure 1a shows a comparison of the optimization performance of the SuPAC-CE algorithm against gradient descent methods on a biochemical calibration task. The median performance and 0.2 and 0.8 quantiles from 20 repeated optimization runs are shown. Figure 1b presents the training and testing performance of the meta-learning approach (Section 5) by visualizing the train meta-score, test meta-score, and test score fluctuation across 150 training iterations. The results showcase SuPAC-CE’s efficiency in minimizing the PAC-Bayes objective and its improved performance in meta-learning.

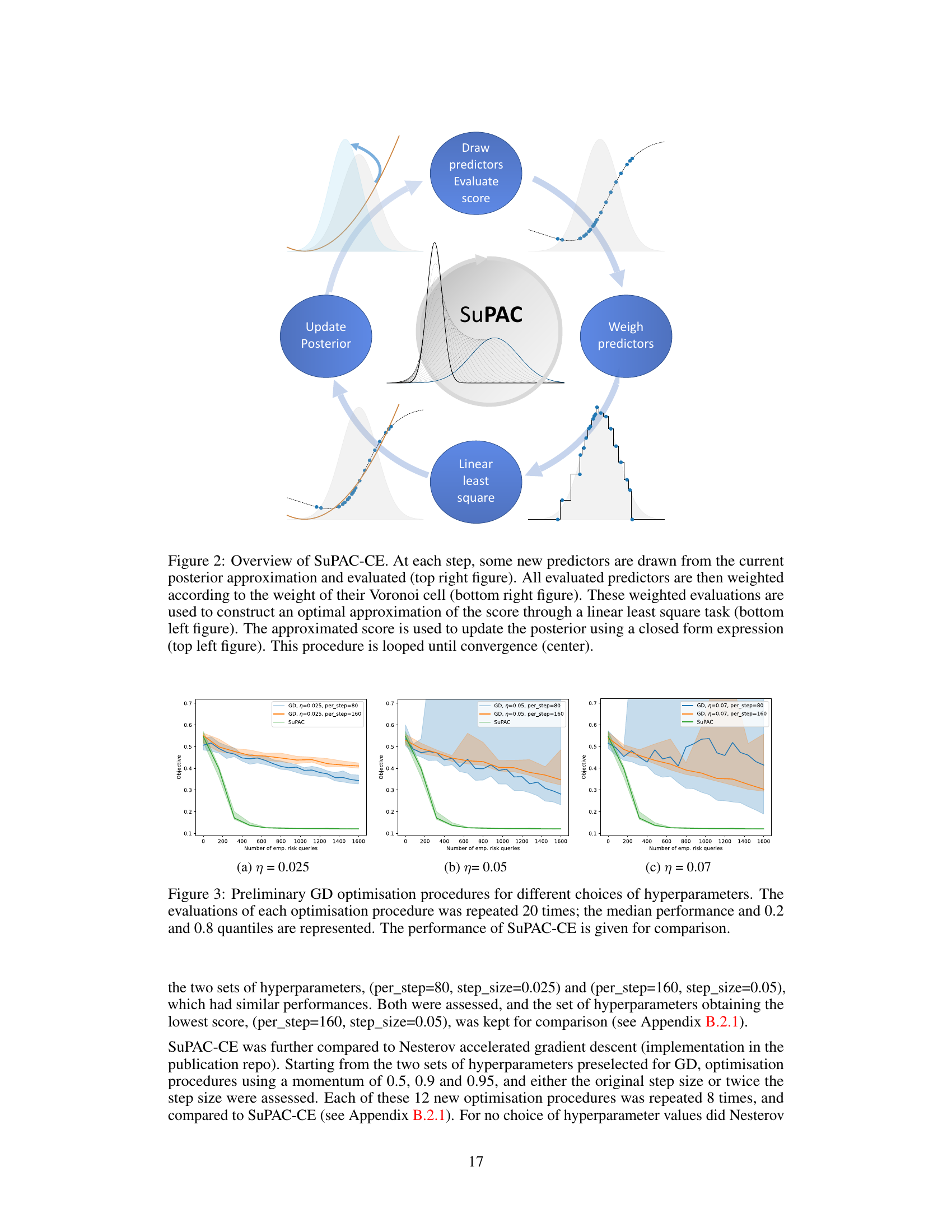
This algorithm describes the Surrogate PAC-Bayes Learning framework. It iteratively optimizes a sequence of surrogate training objectives, replacing the empirical risk with a projection onto a lower-dimensional space. This makes the optimization more computationally tractable, particularly for models with expensive risk evaluations.

In-depth insights

#

Surrogate PAC-Bayes

#

The core idea behind “Surrogate PAC-Bayes” is to address the computational challenges of directly optimizing PAC-Bayes generalization bounds. Traditional PAC-Bayes methods often involve computationally expensive calculations, such as repeatedly evaluating the empirical risk. This approach cleverly introduces surrogate training objectives that approximate the original bound but are significantly more tractable. The key strategy is to project the empirical risk onto a lower-dimensional functional space, making it far easier to query. This enables the development of iterative learning algorithms where each iteration optimizes a surrogate, leading to a more efficient optimization of the original PAC-Bayes bound. Theoretical guarantees are provided to ensure that optimizing these surrogates implicitly optimizes the original bounds. The framework’s versatility is highlighted through its application to meta-learning, demonstrating its adaptability to various machine learning scenarios. The method’s effectiveness is further validated through numerical experiments, proving its practical significance.

Meta-Learning

#

The section on meta-learning explores a novel application of surrogate PAC-Bayes, leveraging its computational efficiency to optimize a meta-objective. Instead of directly optimizing the generalization bound across all tasks, the authors propose iteratively optimizing a sequence of surrogate objectives. This clever approach significantly reduces the computational cost, particularly relevant for complex models where evaluating the empirical risk is expensive. The meta-learning strategy facilitates the learning of a prior distribution that generalizes well across various tasks. By learning the prior, the algorithm simultaneously improves the efficiency of the inner PAC-Bayes learning loop and obtains tighter generalization bounds. A closed-form expression for the meta-gradient further simplifies this process, making the overall approach more tractable and efficient. The empirical results on a complex biochemical problem underscore the practical effectiveness of this approach in meta-learning contexts.

SuPAC Algorithm

#

The SuPAC algorithm, a novel iterative learning method, tackles the computational challenges of optimizing PAC-Bayes generalization bounds by introducing surrogate training objectives. Instead of directly optimizing the empirical risk, which can be computationally expensive, especially for complex models, SuPAC projects the risk onto a lower-dimensional functional space. This projection is significantly more efficient to query, enabling faster iterative optimization. The algorithm’s core strength lies in its theoretical grounding, ensuring that iteratively optimizing these surrogates effectively approximates the original PAC-Bayes bound. This is particularly valuable in scenarios involving computationally intensive tasks. Practical applications, such as the use of SuPAC in the meta-learning framework, demonstrate the algorithm’s versatility and potential for solving real-world problems. Its application to an industrial biochemical model showcases its effectiveness in handling stiff ODEs, further highlighting its potential impact across diverse machine learning applications.

Industrial Use

#

The potential for industrial use of the research presented is significant, particularly in sectors with computationally intensive processes. The core methodology, Surrogate PAC-Bayes Learning (SuPAC), directly addresses the computational bottleneck of optimizing PAC-Bayes bounds by employing surrogate objectives. This approach makes the technique suitable for deploying models in contexts with computationally expensive risk functions, such as those involving complex simulations or solving stiff differential equations. Industrial applications in biochemical processes, physics modeling, or other areas with computationally intensive aspects are likely candidates. The efficacy of SuPAC, demonstrated through experiments inspired by an anaerobic digestion model, suggests real-world applicability. Further investigation into the scalability of SuPAC for high-dimensional data is needed, but the closed-form meta-objective expressions within a meta-learning framework offer promising directions for future expansion into more complex industrial applications. The ability to leverage previously computed risk evaluations also enhances the practicality and efficiency of this approach in real-world deployments.

Future Work

#

Future research directions stemming from this work could explore several promising avenues. Extending the surrogate framework to higher-dimensional spaces is crucial for broader applicability, especially in deep learning. Investigating alternative approximation techniques beyond orthogonal projections, such as those employing Gaussian processes, could enhance efficiency and accuracy. A thorough theoretical analysis of the convergence properties of surrogate methods under various conditions is also warranted. Furthermore, the practical impact of the surrogate PAC-Bayes approach on different machine learning tasks should be evaluated. This includes exploring its benefits in tasks with complex models, like those involving ODE or PDE solvers. Finally, integrating surrogate techniques with meta-learning frameworks offers exciting prospects, potentially leading to more efficient and effective meta-learning algorithms. The focus should be on improving the efficiency and stability of meta-gradient estimation and minimizing the number of risk queries required. Addressing these points would significantly advance the field and solidify the practical utility of the proposed method.

More visual insights

#

More on figures

This figure illustrates the workflow of the SuPAC-CE algorithm. It shows how new predictors are sampled from the current posterior distribution, their scores are evaluated, weighted according to their Voronoi cells, and used in a linear least squares task to approximate the score function. The approximated score is then used to update the posterior distribution iteratively, until convergence is achieved.

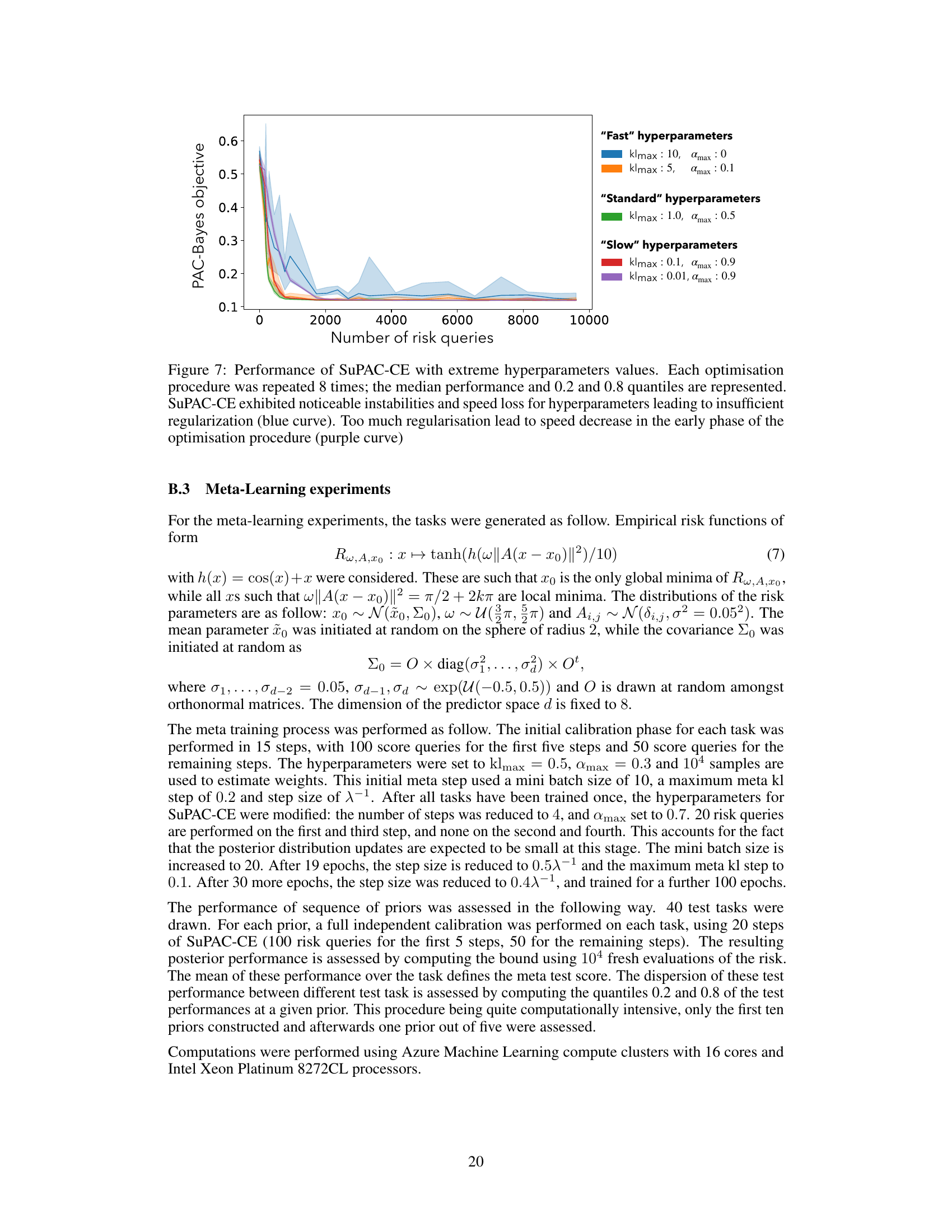
The figure compares the performance of the proposed SuPAC-CE algorithm to standard gradient descent for an industrial biochemical calibration task (Figure 1a). It also shows results for a meta-learning approach where the algorithm learns a better prior (Figure 1b). The key finding is that SuPAC-CE is significantly more efficient in minimizing the PAC-Bayes bound than gradient descent.

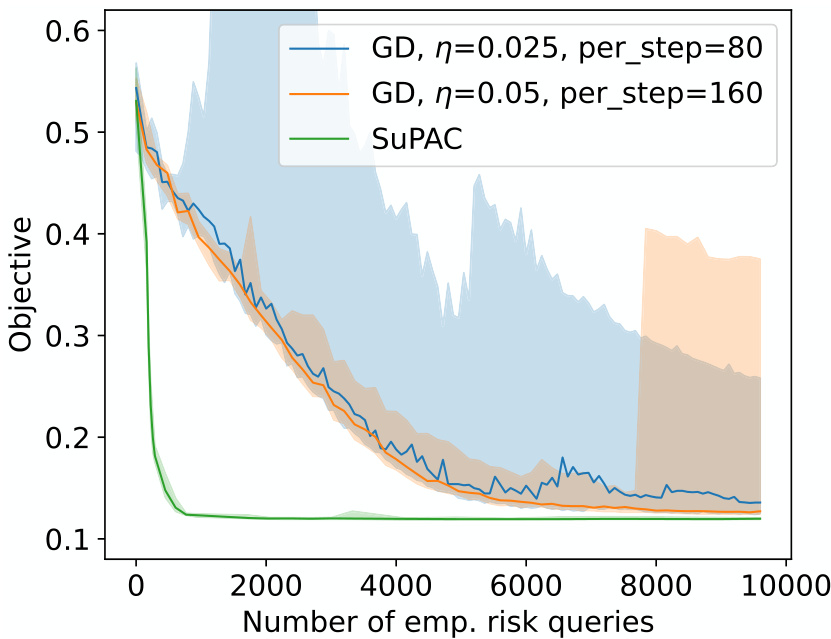
This figure displays the results of two experiments. The first (Figure 1a) compares the performance of SuPAC-CE to gradient descent methods on a biochemical calibration task, showing SuPAC-CE’s superior performance in minimizing the PAC-Bayes objective. The second (Figure 1b) illustrates the results of applying SuPAC-CE to a meta-learning framework (as discussed in Section 5), demonstrating the algorithm’s effectiveness in improving meta-objective scores across multiple training tasks and generalizing well to unseen test tasks.

This figure shows the results of experiments comparing the performance of the proposed SuPAC-CE algorithm with gradient descent methods for a biochemical calibration task (Figure 1a) and a meta-learning approach (Figure 1b). Figure 1a illustrates that SuPAC-CE is more efficient and stable than gradient descent in minimizing the PAC-Bayes bound. Figure 1b demonstrates the meta-learning approach where SuPAC-CE significantly improves the meta-objective, showing its ability to learn a good prior for better generalization.

This figure shows the results of experiments comparing the performance of the proposed algorithm SuPAC-CE with gradient descent methods on a biochemical calibration task (Figure 1a) and a meta-learning approach (Figure 1b). Figure 1a shows that SuPAC-CE is significantly more efficient than gradient descent at minimizing the PAC-Bayes bound. Figure 1b demonstrates the effectiveness of the meta-learning strategy for improving generalization performance.

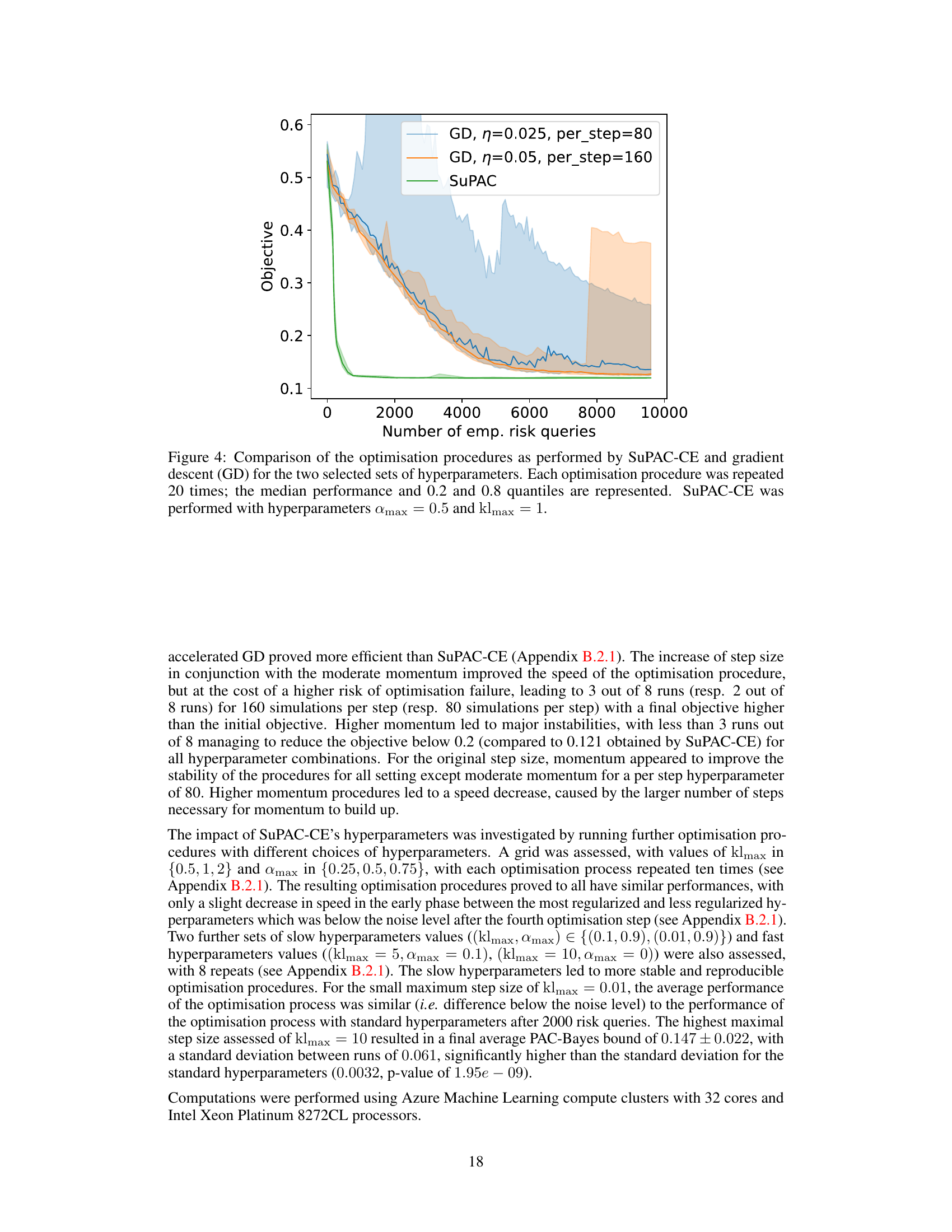
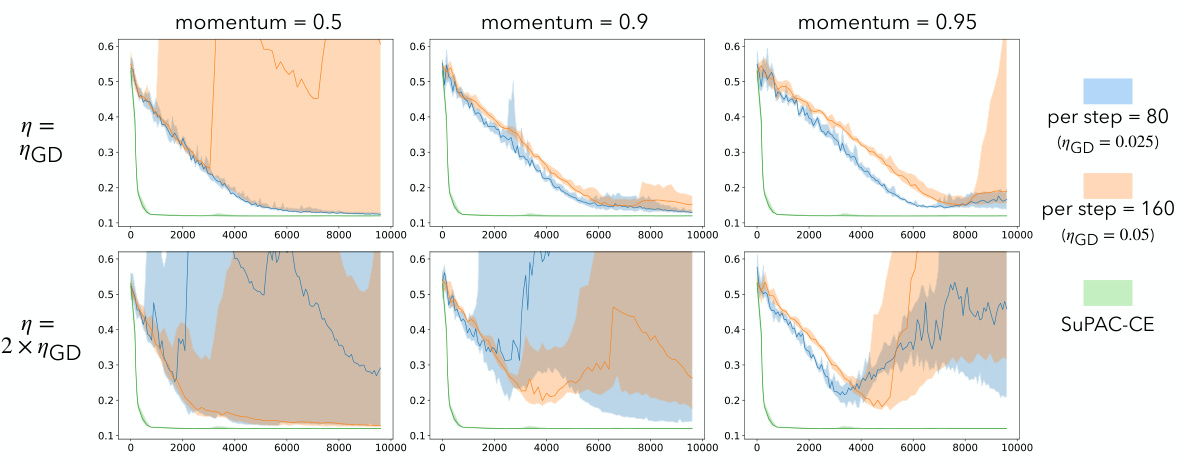
This figure shows the performance of the SuPAC-CE algorithm under various hyperparameter settings. The x-axis represents the number of risk queries, and the y-axis represents the PAC-Bayes objective. Multiple runs are shown for each set of hyperparameters, indicating the variability in performance. The results demonstrate a trade-off between speed and stability; insufficient regularization leads to instability, while excessive regularization slows down the optimization process.

Full paper

#