Understanding the Differences in Foundation Models: Attention, State Space Models, and Recurrent Neural Networks

iF7MnXnxRw

Jerome Sieber et el.

TL;DR
#

Foundation models, crucial for AI, often rely on softmax attention with its quadratic complexity. This limits their application in long sequences. Alternative architectures like linear attention, State Space Models (SSMs), and Recurrent Neural Networks (RNNs) offer potential solutions, but lack a unified understanding of their shared principles and differences. This hinders rigorous comparison and efficient model design.

This research introduces the Dynamical Systems Framework (DSF) to address these issues. DSF provides a common representation for these architectures, enabling rigorous comparisons and revealing novel insights. For example, it details conditions under which linear attention and SSMs are equivalent, and when softmax attention can be approximated. Empirical validations further support these theoretical findings, showcasing the DSF’s potential to guide the development of future efficient and scalable foundation models.

Key Takeaways
#

Why does it matter?
#

This paper is crucial for researchers working on foundation models. It offers a novel framework for comparing different model architectures, enabling more efficient model development. By highlighting the relationships between attention, recurrent neural networks, and state space models, it opens new avenues for research and informs the systematic development of future foundation models. This is highly relevant given the current focus on improving the efficiency and scalability of large language models.

Visual Insights
#

This figure compares the performance of linear and softmax attention mechanisms on two different MQAR tasks with varying sequence lengths and numbers of key-value pairs. The model size is fixed, but the state expansion (n) is varied. The best results from a learning rate sweep are reported, showing how linear attention’s performance approaches that of softmax attention as state expansion increases.

This table compares the performance of three different normalization functions (exponential, softplus, and sigmoid) used in the normalized attention mechanism on two benchmark tasks: LRA Image and MQAR (with sequence length L=512 and KV-pairs=64). The table shows that the exponential normalization function performs best on both tasks.

In-depth insights
#

DSF: A Unified View
#

The Dynamical Systems Framework (DSF) offers a unified perspective on various foundation models by representing them within a common mathematical framework. This approach facilitates direct comparisons between seemingly disparate architectures like attention mechanisms, recurrent neural networks (RNNs), and state space models (SSMs), revealing shared principles and subtle differences that influence performance and scalability. The DSF’s power lies in its ability to rigorously analyze these models through a control-theoretic lens, providing valuable insights into their behavior and guiding the development of more efficient and scalable foundation models. Key advantages include simplifying model relationships, facilitating the identification of equivalent architectures under specific conditions, and offering a systematic approach to improving existing models by transferring beneficial aspects of different architectures.

Attention’s Limits
#

The heading “Attention’s Limits” aptly captures the inherent constraints of the attention mechanism, a cornerstone of modern deep learning. Quadratic complexity with respect to sequence length is a major drawback, significantly hindering the processing of long sequences. This limitation stems from the need to compute pairwise relationships between all tokens in the input, rendering it computationally expensive and impractical for many real-world applications demanding long-context understanding. Alternatives like linear attention and state space models are explored as more efficient options, but they often come with trade-offs in terms of expressiveness or accuracy, especially in complex scenarios involving intricate relationships between distant tokens. The exploration of such limitations emphasizes the need for innovation in designing more scalable and efficient architectures to overcome these attention bottlenecks and realize the full potential of deep learning models in handling extensive and varied input data.

SSM’s Advantages
#

State Space Models (SSMs) offer several compelling advantages over traditional attention mechanisms in the context of foundation models. Computational efficiency is a key benefit, as SSMs exhibit linear time complexity with respect to sequence length, unlike the quadratic complexity of softmax attention. This makes SSMs significantly more scalable for processing long sequences, a crucial factor in handling extensive datasets or generating long-range dependencies. Improved performance on benchmarks such as the Long Range Arena (LRA) demonstrates SSMs’ effectiveness in capturing long-range dependencies more accurately than attention-based models. Theoretical elegance provides another advantage. SSMs benefit from a rich mathematical framework, enabling easier analysis of their properties and facilitating principled design choices. The ability to incorporate recurrence naturally makes SSMs suitable for representing sequential data, leading to enhanced modeling capabilities. Finally, the flexibility of SSMs allows for various parameterizations, enabling the design of specialized SSM variants with tailored properties, such as selective SSMs, that further optimize efficiency and performance for specific tasks. These aspects highlight SSMs as a promising avenue for developing future foundation models that are both efficient and highly capable.

RNN Enhancements
#

Recurrent Neural Networks (RNNs), despite their inherent sequential processing capabilities, have historically faced challenges in handling long sequences due to vanishing/exploding gradients. The research paper explores enhancements to RNN architectures, aiming to overcome these limitations and improve their performance, particularly in long-range dependency tasks. This involved exploring modifications to existing RNN variants like LSTMs (Long Short-Term Memory) by introducing novel gating mechanisms or state expansion techniques. The goal is to increase the model’s capacity to retain and process information over extended time horizons. A key theme is the comparison of RNN enhancements with alternative architectures like state space models and attention mechanisms within a unified framework. This comparative analysis highlights the strengths and weaknesses of each approach, allowing researchers to better understand how to leverage the unique attributes of different architectures. Specifically, selective state space models (SSMs) are contrasted with enhanced RNNs, providing valuable insights into their similarities and differences in performance and computational efficiency. The ultimate aim is to inform the design of more efficient and scalable foundation models that can excel in various sequence modeling tasks. State expansion and improved normalization strategies emerge as crucial considerations for enhancing both RNNs and attention mechanisms.

Future Research
#

Future research directions stemming from this work could explore several key areas. Extending the Dynamical Systems Framework (DSF) to encompass non-linear systems and hybrid models would significantly broaden its applicability. Investigating the theoretical implications of various normalization strategies within the DSF, and their impact on model expressivity and long-range dependency, is crucial. Empirical validation of the DSF’s predictions on larger, more complex datasets and tasks is also necessary to establish its robustness and generalizability. Furthermore, exploring the relationship between state expansion and model performance in recurrent architectures through the lens of DSF warrants further attention. Finally, applying the DSF to guide the design of novel, more efficient foundation models by leveraging insights from different architectural classes is a promising future avenue. This includes exploring the conditions under which approximations of softmax attention are valid and the development of hybrid models that combine the strengths of attention, SSMs, and RNNs.

More visual insights
#

More on figures

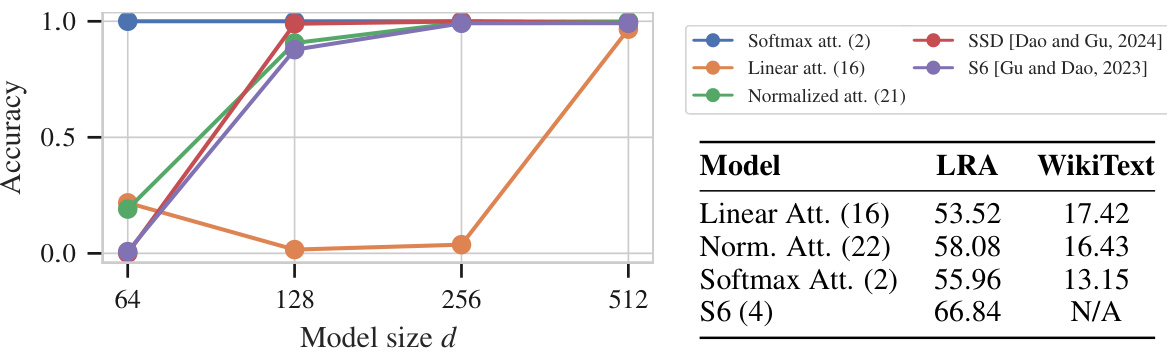
The figure compares the performance of different attention mechanisms (softmax, linear, normalized) and state space models (S6, SSD) on the MQAR benchmark task with sequence length L=512 and KV-pairs=64. The model size ’d’ is varied, and the best accuracy achieved during a learning rate sweep (using np.logspace(-4, -2, 4)) is reported for each model and size, with a fixed state expansion ’n’ of 128.

This figure compares the performance of a standard qLSTM model with a modified version where the state transition matrix Aᵢ is replaced with a reversed sigmoid function (equation 23 from the paper). The comparison is done across three different MQAR tasks, each varying in sequence length and the number of key-value pairs, and across multiple model sizes (d). The orange lines show the performance of the modified qLSTM (using equation 23), while the blue lines show the performance of the standard qLSTM. The results demonstrate the improvement achieved by using the modified state transition, particularly noticeable in the tasks with longer sequences.

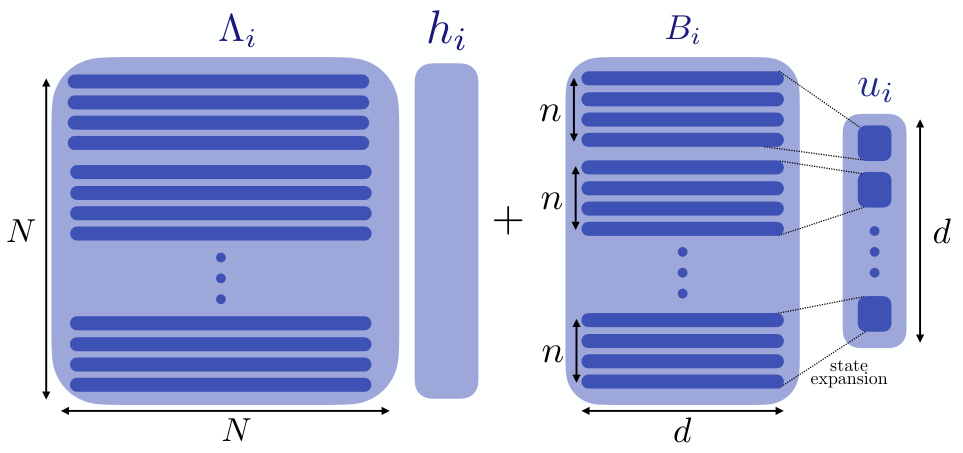
This figure visually represents the matrix dimensions in the Dynamical Systems Framework (DSF) described by the recurrence equation: hi = Aihi-1 + Biui. It highlights the hidden state (hi) with dimension N, the diagonal state transition matrix (Ai) with dimension N x N, and the input matrix (Bi) with dimension N x d. The diagram also illustrates the concept of ‘state expansion,’ where the input dimension d is expanded by a factor of n, resulting in a hidden state with dimension N = nd.

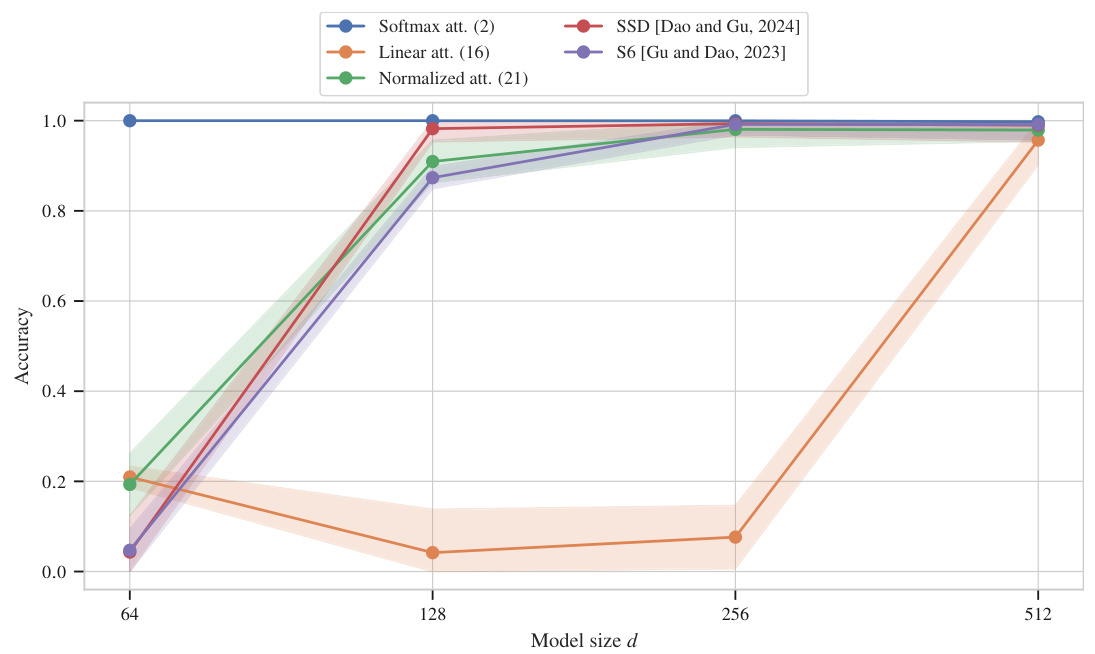
This figure compares the performance of linear and softmax attention on two different MQAR tasks with varying sequence lengths and numbers of key-value pairs. The model size (d) is kept constant at 512, while the state expansion (n) is varied. The results show that as the state expansion increases, the accuracy of linear attention approaches that of softmax attention.

This figure compares the performance of a standard quasi LSTM (qLSTM) against a modified version where the state transition matrix is replaced by a reversed sigmoid of the projected input, inspired by the S6 model. The results are shown for three different MQAR tasks with varying sequence lengths and numbers of key-value pairs, and for different model sizes (d). The shaded areas represent the standard deviation across multiple runs with different random seeds.

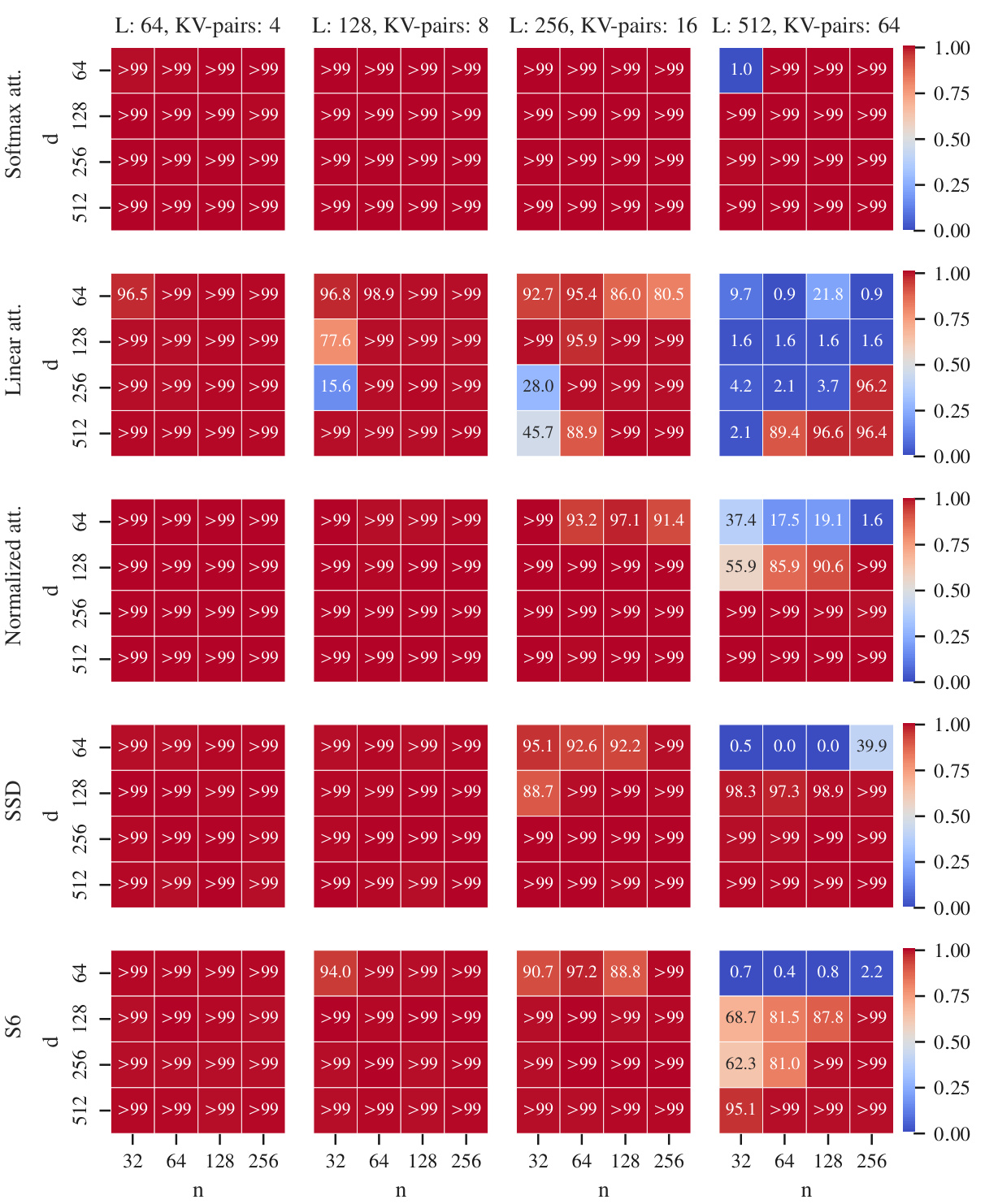
This figure shows the accuracy of different models (softmax attention, linear attention, normalized attention, S6, and SSD) on four different MQAR tasks with varying sequence lengths and key-value pairs. The model size (d) and state expansion (n) are also varied. The heatmap shows the accuracy for each combination of model, task, d, and n, highlighting the impact of these parameters on performance. Note that only the best accuracy from a learning rate sweep is reported for each configuration.

TL;DR#

Key Takeaways#

Why does it matter?#

Visual Insights#

In-depth insights#

DSF: A Unified View#

Attention’s Limits#

SSM’s Advantages#

RNN Enhancements#

Future Research#

More visual insights#

Full paper#