Dynamic Rescaling for Training GNNs

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for GNN researchers as it introduces dynamic rescaling, a novel technique for influencing GNN training. It offers insights into training dynamics, especially concerning homophilic/heterophilic graphs and layer-wise learning, potentially leading to faster training and better generalization. The identified grokking-like phenomena also opens new research avenues.

Visual Insights

#

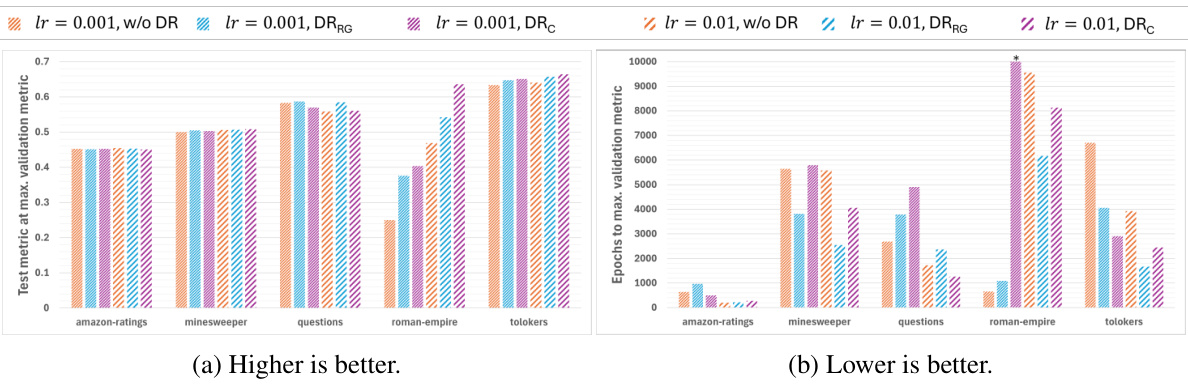
This figure shows the performance of a 5-layer Graph Attention Network (GAT) trained with different dynamic rescaling settings and learning rates. The results are presented for five different datasets (roman-empire, amazon-ratings, minesweeper, questions, and tolokers). The performance metric used is accuracy for roman-empire and amazon-ratings, and ROC AUC for the other three datasets. The figure compares performance with no dynamic rescaling (w/o DR), dynamic rescaling based on weight norms (DRW), dynamic rescaling based on relative gradients (DRRG), and a combination of both (DRC). The results show that applying DRRG or DRC can sometimes lead to improved performance compared to no dynamic rescaling, especially with a learning rate of 0.01. The asterisk (*) indicates that training continued for more than 10,000 epochs in certain cases.

This table presents the results of training a 5-layer Graph Attention Network (GAT) using four different dynamic rescaling methods: no dynamic rescaling (w/o DR), dynamic rescaling with respect to weight norms (DR_W), dynamic rescaling with respect to relative gradients (DR_RG), and a combination of both (DR_C). The table shows the mean and 95% confidence interval of the test metric (accuracy for roman-empire and amazon-ratings, ROC AUC for others) achieved at the epoch with the best validation performance, across 10 different random train/test splits. The best learning rate from a set of options was used for each setting. The asterisk (*) indicates statistically significantly better performance compared to no dynamic rescaling.

In-depth insights

#

Dynamic Rescaling in GNNs

#

Dynamic rescaling, applied to Graph Neural Networks (GNNs), offers a novel approach to training optimization. By exploiting the inherent rescale invariance property of certain GNN architectures, such as Graph Attention Networks (GATs), this method allows for the manipulation of network parameters and gradients without altering the network’s function. This provides a powerful tool to influence training dynamics. The core idea revolves around dynamically scaling parameters during training to maintain a balanced state according to various criteria, such as balancing parameter and gradient norms. This balance can significantly impact training speed, generalization performance, and even layer-wise learning dynamics. Interestingly, the technique suggests that different training strategies might be optimal for homophilic and heterophilic graphs, with homophilic graphs potentially benefiting from focused learning in initial layers while heterophilic ones might thrive on a balanced approach. Furthermore, the method introduces the exciting possibility of controlling layer-wise learning speeds, opening doors to explore phenomena resembling ‘grokking’. Overall, dynamic rescaling presents a promising avenue for enhancing GNN training, highlighting the potential for more efficient and effective learning.

Balancing Criteria & Impact

#

The concept of balancing in neural network training, particularly within the context of Graph Neural Networks (GNNs), is explored. Two primary balancing criteria are investigated: balancing the squared L2-norms of incoming and outgoing parameters and balancing relative gradients. The choice of criterion significantly impacts training dynamics. Balancing based on relative gradients often proves superior, leading to faster convergence and improved generalization, especially in heterophilic graph scenarios. The importance of this approach is highlighted through experimental results, demonstrating that the balanced state, dynamically maintained during training, enables the use of larger learning rates without sacrificing stability or generalization. This is linked to the overall goal of achieving flatter minima during optimization. Moreover, the study reveals intriguing connections between layer-wise training speed control, dynamic rescaling, and grokking-like phenomena, suggesting that layer-wise imbalances may be purposefully exploited to improve training efficiency and generalization, particularly for specific types of graph structures.

Layer-wise Learning Order

#

The concept of ‘Layer-wise Learning Order’ explores how controlling the training speed of individual layers in a neural network, particularly Graph Neural Networks (GNNs), impacts performance. Dynamic rescaling, a technique that scales network parameters and gradients while maintaining loss invariance, provides a mechanism to manipulate this learning order. The paper investigates how prioritizing learning in certain layers (e.g., earlier layers for homophilic graphs, balanced learning for heterophilic graphs) affects both training speed and generalization. Homophilic graphs, exhibiting similar node features within neighborhoods, may benefit from concentrating initial learning on early layers. Conversely, heterophilic graphs, showing dissimilar features, might better leverage balanced learning across all layers. The study also explores the intriguing link between layer-wise learning control and the phenomenon of grokking, where improved generalization occurs after a period of seemingly minimal progress.

Grokking-like Phenomena

#

The study explores the intriguing phenomenon of “grokking-like behavior” in graph neural networks (GNNs). It reveals that delayed learning in specific layers, rather than solely the final layer, can induce this behavior, where validation loss significantly drops after initial near-zero training loss. This challenges the existing understanding of grokking. Interestingly, this delayed learning can be strategically controlled via dynamic rescaling of network parameters, demonstrating that manipulating the order in which layers learn can influence generalization performance. The experiments on both synthetic and real-world data highlight the potential connection between balanced layer-wise learning and the absence of grokking, suggesting that maintaining balanced training dynamics may prevent or mitigate grokking. The findings present a nuanced perspective on the training dynamics of GNNs and suggest avenues for future research into both grokking and the optimization of GNN training.

Limitations and Future Work

#

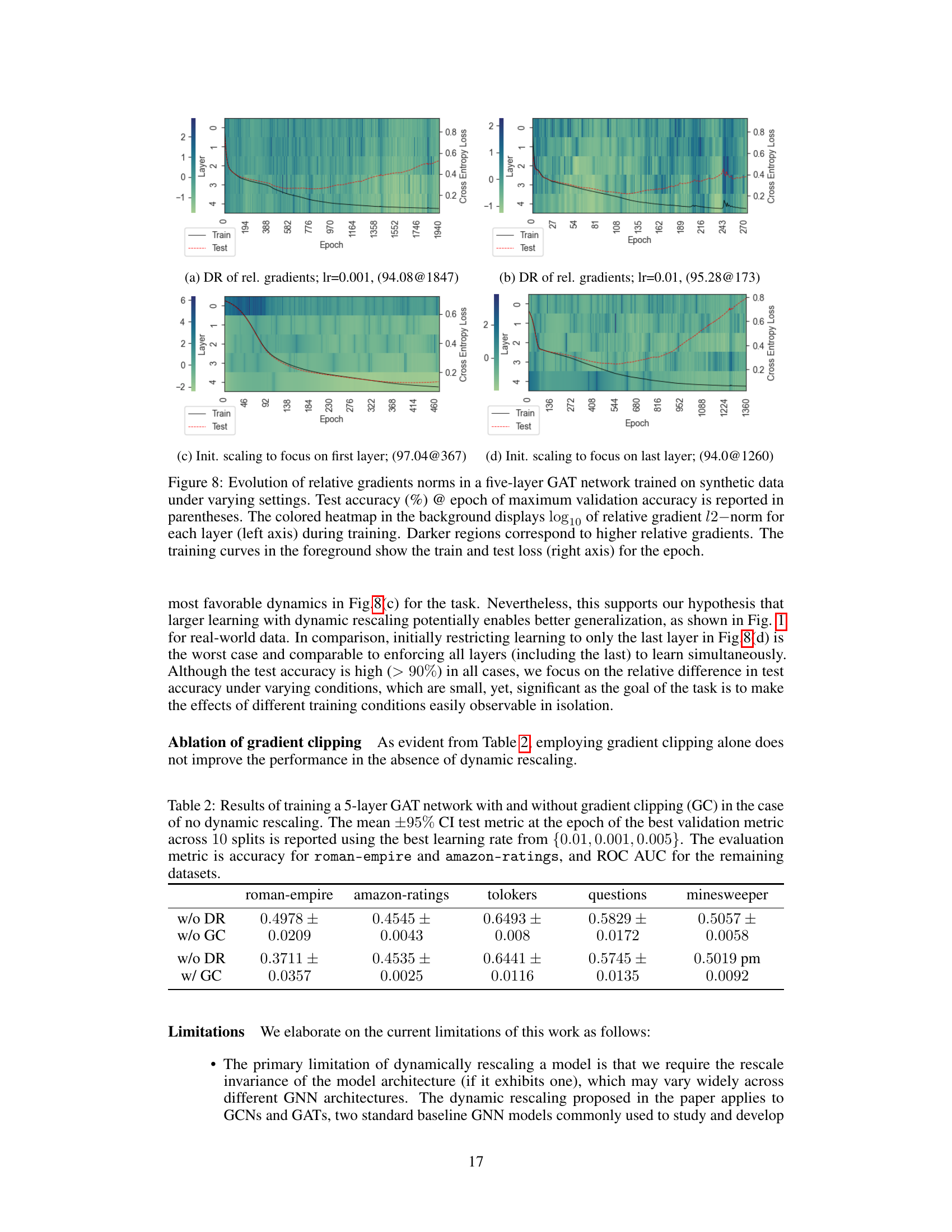
This research demonstrates a novel approach to training Graph Neural Networks (GNNs) by dynamically rescaling network parameters and gradients, but acknowledges several limitations. The primary limitation is the dependence on rescale invariance, a property not held by all GNN architectures. While the method shows promise even when this invariance is violated, a more robust approach is needed. Further research is needed to investigate the impact of different rescaling criteria and to develop methods to select criteria effectively. The computational cost of repeated rescaling is another concern that needs attention. Future work should focus on extending the approach to a wider variety of GNNs, exploring alternative rescaling strategies and optimization techniques to address scalability. Addressing potential numerical instabilities, possibly by leveraging more sophisticated techniques than gradient clipping, is also crucial. Finally, a deeper theoretical understanding of the relationship between layer-wise learning and generalization is needed, especially concerning grokking-like phenomena.

More visual insights

#

More on figures

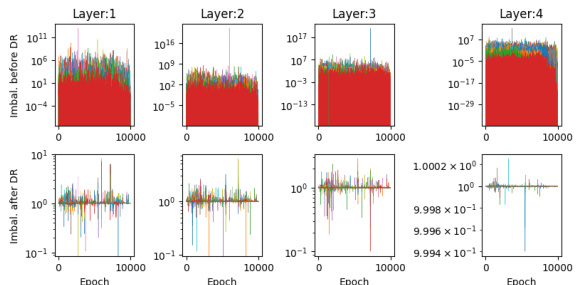
This figure shows how balanced the network is, based on a specific criterion (Eq. 5 in the paper), both before and after applying a rebalancing technique. The x-axis represents the training epoch, and the y-axis shows the degree of imbalance. Each line represents a different neuron in the network. The goal is to minimize imbalance (bring the value toward zero), which is done by rescaling weights and gradients as described in the paper. The top row of plots illustrates the imbalance before rebalancing, while the bottom row depicts the situation after rebalancing every 10 epochs. The figure is a visualization of the dynamic rescaling technique used to maintain balance in the network during training.

This figure shows the performance of a 5-layer Graph Attention Network (GAT) trained with different dynamic rescaling settings and learning rates. The dynamic rescaling methods are denoted by DRW, DRRG, and DRC, representing dynamic rescaling with respect to weight norms, relative gradients, and a combination of both, respectively. The performance is evaluated using accuracy for the datasets roman-empire and amazon-ratings, and ROC AUC for minesweeper, questions, and tolokers. The results are averaged across 10 different random train/test splits. The asterisk (*) indicates that training ran for more than 10,000 epochs.

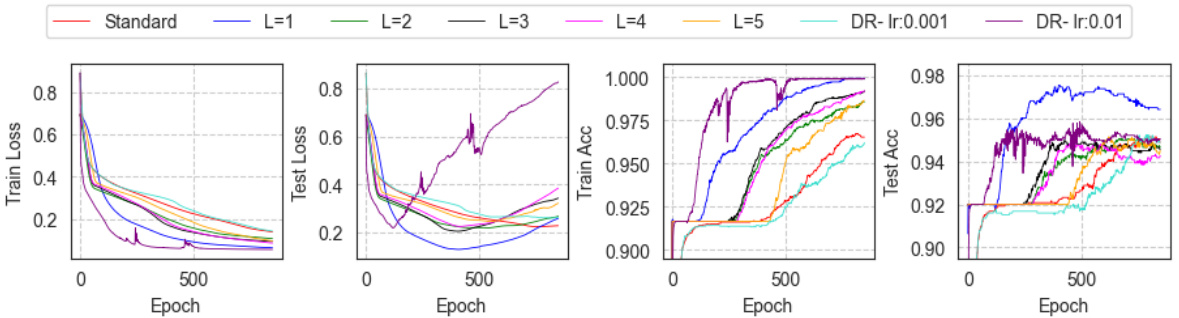
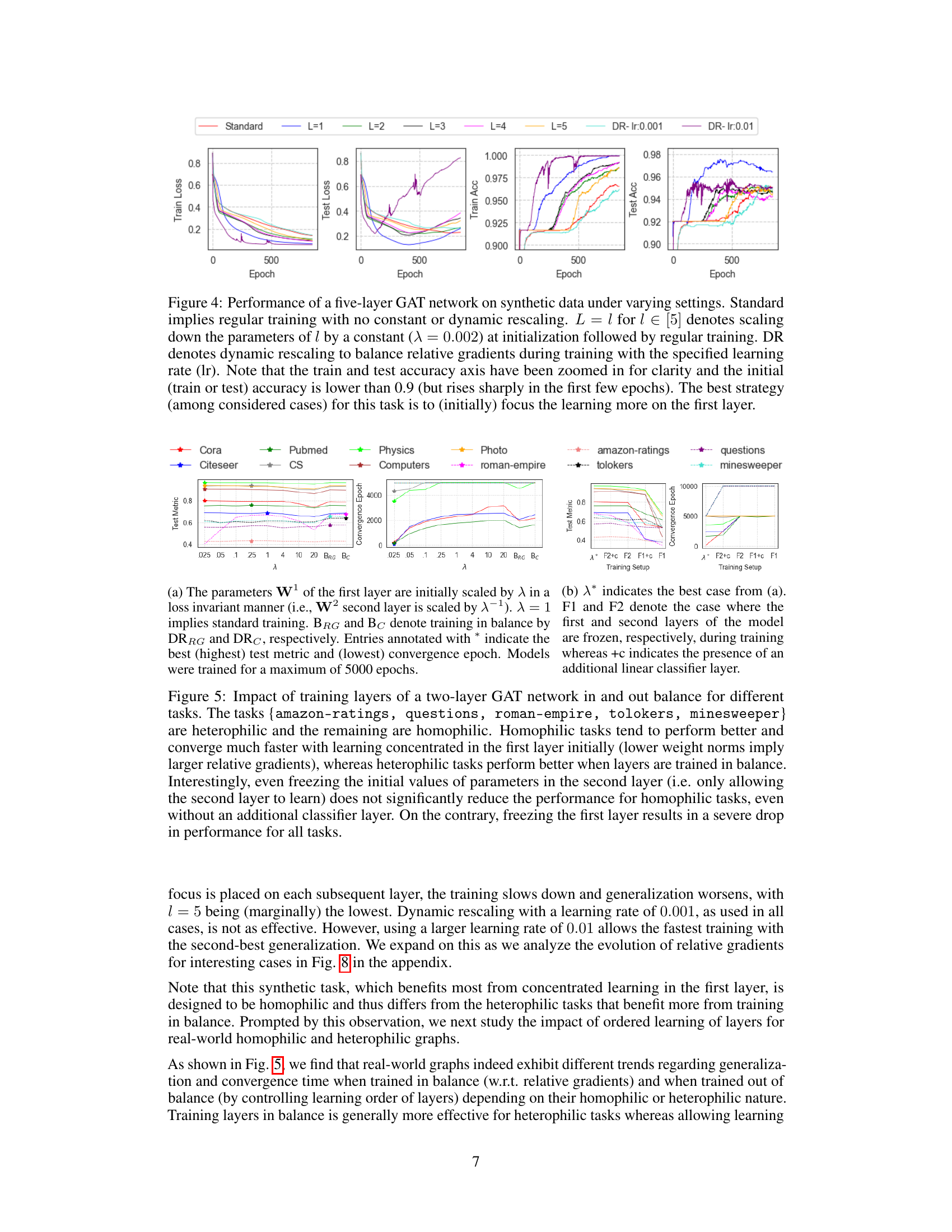
This figure shows the performance of a 5-layer GAT network on synthetic data using various training strategies. The standard training shows the baseline performance. L=1 to L=5 represents training where only the layers 1 to 5 are initially scaled-down, respectively, by a constant factor before starting regular training. DR represents dynamic rescaling methods to balance relative gradients during the training process using the specified learning rates. The results show that focusing training on the first layer is the most effective strategy for this particular synthetic task. The graphs show both the training and test loss, as well as training and test accuracy over the epochs.

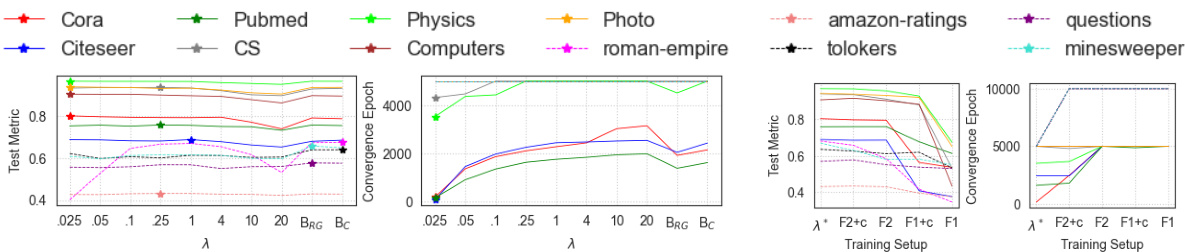
This figure displays the results of experiments on various datasets, categorized as homophilic or heterophilic. It shows the impact of different training strategies on the performance (test metric and convergence epoch) of a two-layer GAT network. The strategies include training with all layers in balance (BRG and BC), training with initially only the first layer active, training with initially only the second layer active, and standard training. Results indicate that for homophilic tasks, focusing learning on the first layer is beneficial, while for heterophilic tasks, balanced training leads to better performance.

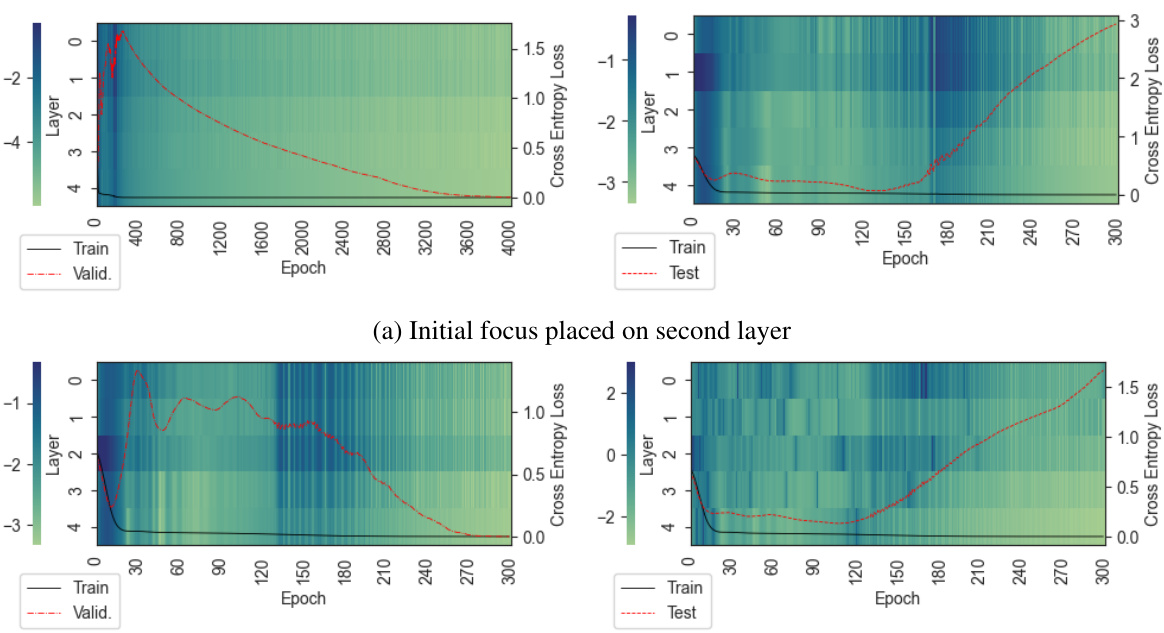
This figure displays the evolution of relative gradient norms (log scale) and loss curves during training of a five-layer GAT network on synthetic data under various settings. The heatmaps show relative gradient ℓ2-norms for each layer, with darker colors indicating larger norms. The line graphs show the training and test loss curves. The figure demonstrates how different initial conditions and learning rate adjustments influence the training dynamics. It helps visualize the impact of concentrating initial learning on specific layers, followed by rebalancing.

This figure shows the layer-wise relative gradient norms and loss curves for a 5-layer GAT trained on the roman-empire dataset. The left panel displays a heatmap of log10(relative gradient norms) over epochs, with separate lines for training, validation, and test loss. The right panel displays the corresponding accuracy curves. The experiment induced grokking-like behavior by initially focusing training on layers 4 or 5 (by scaling down initial parameters) and then rebalancing every 10 epochs starting at epoch 1000. Rebalancing leads to a sharp drop in validation and test loss, and a rapid increase in test accuracy, demonstrating a grokking-like phenomenon.

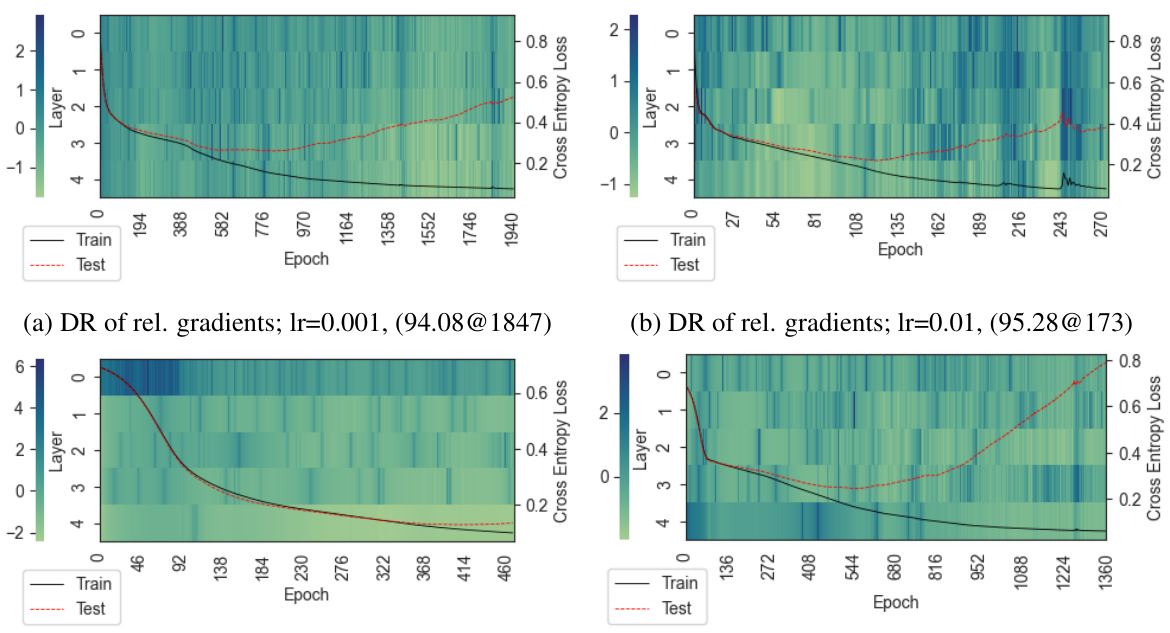
This figure shows the evolution of relative gradient norms (in log10 scale) and training/test loss curves for a five-layer GAT network trained on a synthetic dataset under different dynamic rescaling settings. The heatmap visualizes the relative gradient norms across different layers during training, highlighting how these norms change over time and across layers. The line plots display the training and testing loss curves, indicating the network’s performance during training and its generalization ability. The caption indicates test accuracy at the best validation epoch for each setting, providing a quantitative measure of the network’s overall performance.

Full paper

#