Sigmoid Gating is More Sample Efficient than Softmax Gating in Mixture of Experts

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it rigorously examines the under-explored sigmoid gating function in Mixture of Experts (MoE) models. It provides a theoretical basis for the empirically observed superior performance of sigmoid gating compared to the widely used softmax gating, especially in handling over-specified models. This opens avenues for improved MoE model design and more efficient machine learning.

Visual Insights

#

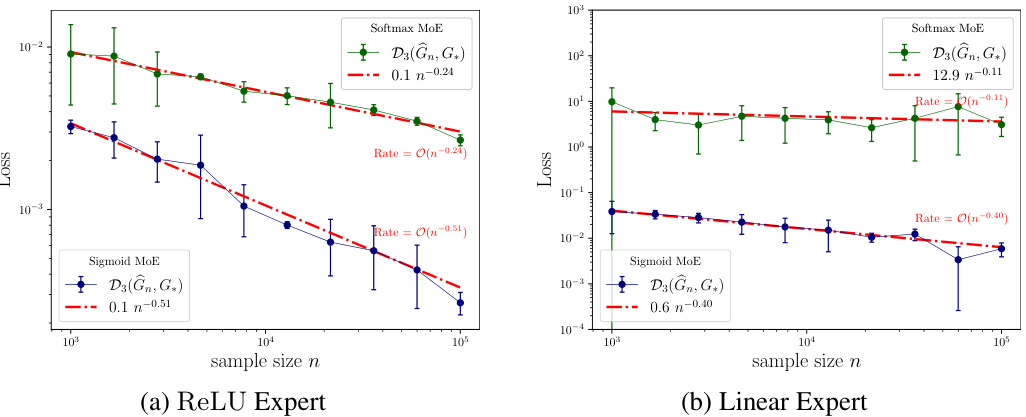
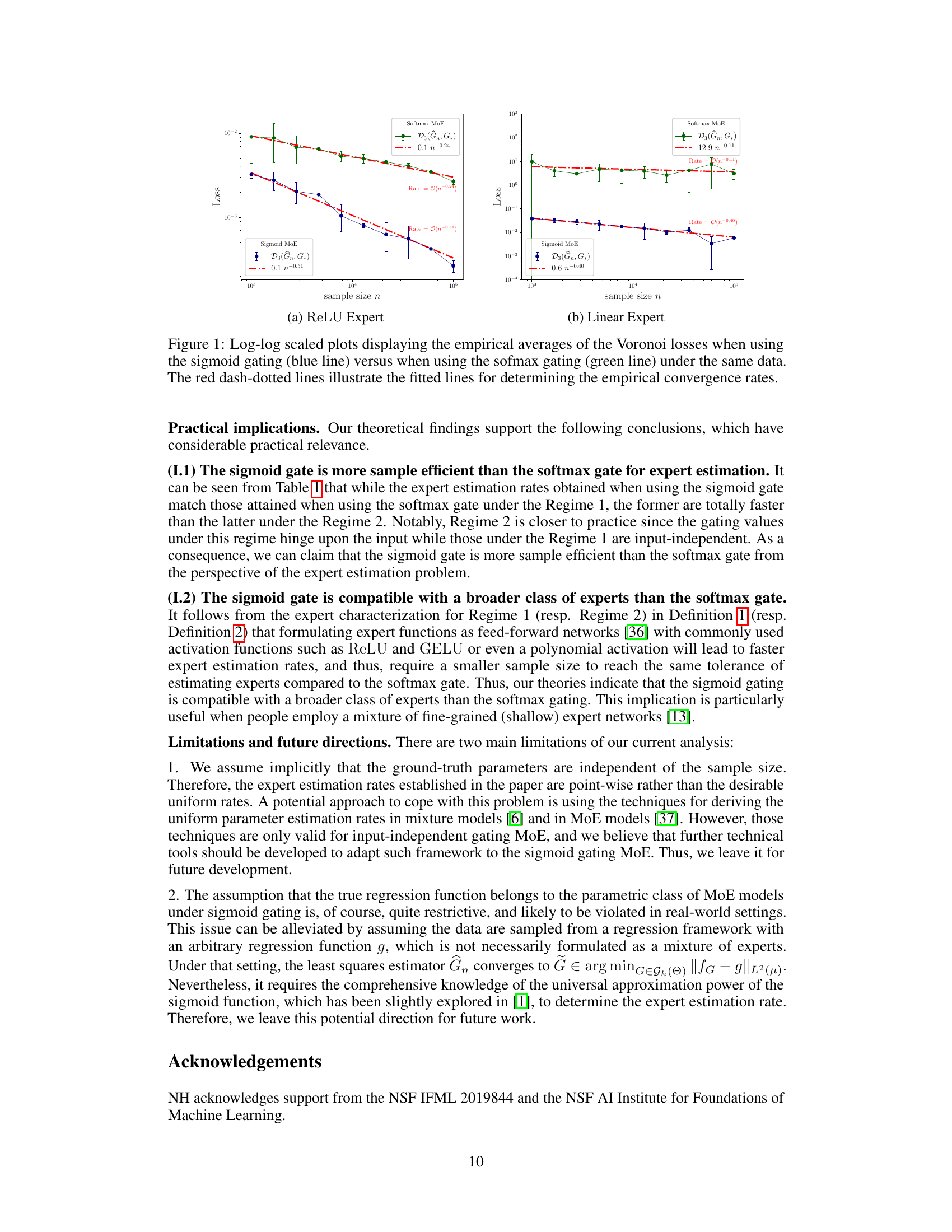
The figure shows the empirical convergence rates for the Voronoi losses using sigmoid and softmax gating methods. Two subfigures are presented, one for ReLU experts and one for linear experts. Each subfigure displays the Voronoi loss (y-axis) plotted against the sample size (x-axis) on a log-log scale. Sigmoid gating shows faster convergence to zero loss for both ReLU and linear expert types, indicating higher sample efficiency compared to softmax gating.

This table summarizes the expert estimation rates achieved using sigmoid and softmax gating functions under two different regimes (Regime 1 and Regime 2) for three types of expert functions: ReLU/GELU experts, polynomial experts, and input-independent experts. It shows that sigmoid gating is more sample efficient than softmax gating, particularly under Regime 2. The rates are given up to logarithmic factors.

In-depth insights

#

Sigmoid Gating

#

The concept of “sigmoid gating” in the context of Mixture of Experts (MoE) models presents a compelling alternative to the commonly used softmax gating. Sigmoid gating mitigates the undesirable competition among experts inherent in softmax, potentially preventing representation collapse and improving model robustness. This is achieved by allowing experts to contribute without strictly competing for dominance, fostering greater diversity and specialization within the MoE architecture. The theoretical analysis suggests that sigmoid gating offers higher sample efficiency, converging faster to accurate expert estimations than softmax, particularly when experts are complex and non-linear. However, the paper also identifies scenarios where additional considerations are needed to fully leverage the benefits of sigmoid gating, highlighting the importance of careful consideration of expert function design and parameterization to maximize its performance advantages. Empirical results support these theoretical findings. Overall, sigmoid gating emerges as a promising direction in MoE research, with the potential to enhance both model accuracy and computational efficiency.

MoE Regression

#

Mixture of Experts (MoE) regression models offer a powerful approach to complex regression problems by combining multiple expert models. Each expert specializes in a specific region of the input space, improving overall model accuracy and flexibility. A crucial aspect is the gating network, which determines the weights assigned to each expert based on the input features. The choice of gating function (e.g., softmax, sigmoid) significantly impacts the model’s performance and efficiency, influencing aspects like representation collapse and sample complexity. Theoretical analyses, such as those on convergence rates and identifiability conditions, are vital for understanding the properties of MoE regression under different gating mechanisms. Empirical evaluations are also essential to validate theoretical findings and demonstrate the practical advantages of specific MoE architectures in real-world scenarios. Furthermore, research into handling over-specified models (more experts than necessary) and efficient training techniques remains a key area of active research in MoE regression.

Convergence Rates

#

The analysis of convergence rates in a machine learning context, particularly within the framework of mixture of experts (MoE) models, is crucial for understanding the model’s learning efficiency and generalization capabilities. Faster convergence rates indicate that the model learns the underlying patterns in the data more quickly, requiring less training data or computational resources. This research focuses on comparing convergence rates between different gating mechanisms, such as sigmoid and softmax gating, within MoE models. The theoretical analysis likely involves deriving bounds on the error of the estimated model parameters as a function of the sample size. The findings suggest that sigmoid gating achieves faster convergence rates than softmax gating under specific conditions, implying improved sample efficiency for model training. Identifiability conditions, related to the nature of expert functions, play a significant role in the convergence behavior and the analysis likely establishes specific conditions under which faster convergence rates are attainable with sigmoid gating. This analysis is important for practical applications, as it guides the choice of gating functions for MoE models based on their learning efficiency and helps avoid representation collapse issues.

Identifiability

#

Identifiability in the context of mixture-of-experts (MoE) models is crucial for ensuring reliable estimation of model parameters. Strong identifiability ensures that the derivatives of the model’s components are linearly independent, leading to faster convergence rates in parameter estimation. This is vital because it prevents ambiguity in determining which expert is responsible for a particular data point. Weak identifiability, a less stringent condition, still allows for efficient estimation but may lead to slightly slower convergence. The paper explores the impact of these different identifiability conditions on the convergence rates under both sigmoid and softmax gating regimes. The choice of gating function and the type of expert network significantly influence identifiability, with sigmoid gating exhibiting better performance, especially for complex expert functions such as those based on ReLU or GELU activations. Conversely, polynomial expert functions present identifiability challenges that result in slower convergence rates. The study emphasizes the importance of considering identifiability conditions when designing and analyzing MoE models to guarantee accurate and efficient expert estimation.

Future Work

#

The paper’s ‘Future Work’ section could productively explore several avenues. Extending the theoretical analysis to non-parametric settings where the true regression function isn’t necessarily a sigmoid-gated MoE would significantly broaden the applicability. This requires addressing the challenges of estimating a completely unknown function and developing robust convergence rates. Investigating the impact of different activation functions beyond ReLU and GELU, especially within the context of deep networks, is another key area. The strong identifiability condition could be relaxed or replaced with weaker assumptions, leading to a more general theory. Exploring alternative optimization algorithms beyond stochastic gradient descent could uncover more sample-efficient methods for parameter estimation and improve practical performance. Finally, conducting more extensive empirical evaluations on real-world datasets with varying scales and complexities is crucial to confirm the theoretical findings and demonstrate the practical advantages of sigmoid gating in various applications. These avenues of future research hold the potential to further solidify the theoretical foundation of sigmoid gating and enhance its applicability in complex machine learning problems.

More visual insights

#

More on tables

This table compares the expert estimation rates achieved by using sigmoid gating versus softmax gating in Mixture of Experts (MoE) models. Three types of expert functions are evaluated: ReLU/GELU networks, polynomial experts, and input-independent experts. The rates are shown for two different regimes of gating parameters, indicating the impact of the gating function on the convergence speed of the expert estimation.

This table summarizes the expert estimation rates achieved using sigmoid and softmax gating functions in Mixture of Experts (MoE) models. Three types of expert functions are considered: ReLU/GELU networks, polynomial experts, and input-independent experts. The table shows the convergence rates under two different regimes (Regime 1 and Regime 2) for both gating functions. The results highlight the superior sample efficiency of sigmoid gating compared to softmax gating, especially for ReLU/GELU and polynomial experts under Regime 2.

Full paper

#