↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Deep neural networks (DNNs) are increasingly used in safety-critical applications, but ensuring they reliably satisfy specific properties remains challenging. Current methods for verifying DNN properties are efficient, but techniques for provably editing a DNN to satisfy a property are lacking, particularly those that are both effective and efficient. Existing approaches, like regularization-based methods, cannot guarantee property satisfaction, while SMT-based methods are computationally expensive.
This paper introduces PREPARED, a novel approach that efficiently solves the provable DNN editing problem. PREPARED uses Parametric Linear Relaxation to transform the NP-hard provable editing problem into a linear program. This enables the construction of tight output bounds for the DNN, parameterized by the new parameters, making the editing process significantly more efficient. The method’s effectiveness and efficiency are demonstrated through various experiments including the VNN-COMP benchmarks, image recognition DNNs, and a geodynamic process model. PREPARED achieves significant speedups over existing techniques and successfully edits DNNs to meet specified properties.
Key Takeaways#
Why does it matter?#
This paper is important because it presents PREPARED, the first efficient and effective technique for provably editing deep neural networks (DNNs). This addresses a critical challenge in deploying DNNs in safety-critical applications, where ensuring the DNN satisfies a desired property is crucial. The method offers significant improvements over existing approaches in terms of efficiency and effectiveness, opening new avenues for research in DNN verification and provable editing techniques. It also has implications for other areas such as image recognition, sentiment classification, and physics modeling.
Visual Insights#

This figure compares different linear relaxations for the ReLU activation function. (a) shows the traditional approach where linear functions overapproximate the ReLU function, and the upper bound is only valid within a specific input range. (b) demonstrates the proposed method, which accurately represents the upper bound for any upper bound input value. (c) illustrates how the proposed method achieves this accurate representation by using linear constraints to capture the epigraph of the ReLU function.
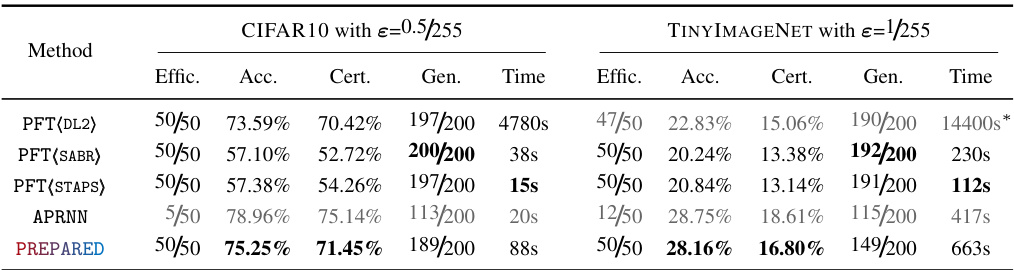
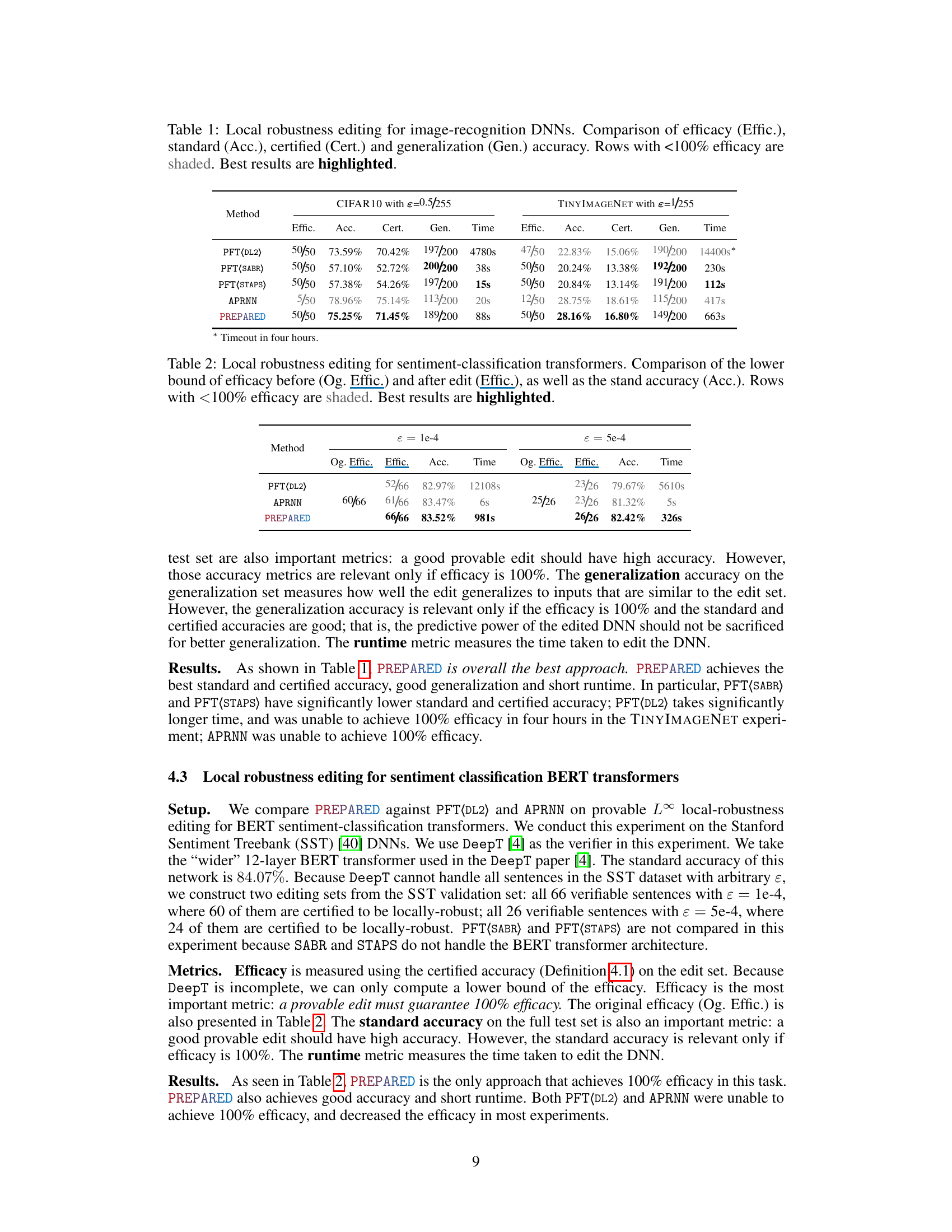
This table presents the results of local robustness editing experiments on image-recognition deep neural networks (DNNs). Two different DNN architectures are evaluated: one trained on CIFAR10 and another trained on TinyImageNet. The efficacy of the editing methods in achieving local robustness (measured as percentage of correctly classified perturbed images) is compared, along with the standard accuracy, certified accuracy (a robustness measure), and generalization accuracy. Several methods are compared, highlighting the efficiency and effectiveness of the PREPARED approach in achieving high efficacy while maintaining good accuracy metrics.
In-depth insights#
Provable DNN Edits#
Provable DNN edits represent a crucial advancement in the field of deep learning, addressing the critical need for trustworthy and reliable AI systems. The core idea involves modifying a deep neural network (DNN) in a verifiable manner, guaranteeing that the resulting network satisfies pre-defined properties. This is particularly important in safety-critical applications where unexpected DNN behavior can have severe consequences. Unlike heuristic methods, provable edits leverage formal verification techniques to mathematically prove the correctness of the modifications, providing a higher level of assurance compared to traditional approaches. This process is computationally intensive, highlighting the need for efficient algorithms and potentially necessitating trade-offs between performance and the level of provable guarantees. The development of effective and scalable techniques for provable DNN edits is key to unlocking the full potential of AI in sensitive domains, where trust and reliability are paramount. Future research may focus on further optimizing the efficiency of verification techniques, expanding the types of properties that can be proven, and developing tools to automate the process, making provable DNN edits accessible to a broader range of users and applications.
Parametric Relaxations#
Parametric relaxations represent a crucial technique in the paper for efficiently solving the NP-hard problem of provably editing deep neural networks (DNNs). The core idea involves creating tight bounds on the DNN’s output, parameterized by the network’s weights. Instead of relying on fixed bounds, the approach constructs bounds that are directly dependent on the model parameters. This parameterization is key to enabling efficient optimization through linear programming, as the constraints become linear functions of the parameters. The use of parametric underapproximations of the activation functions’ epigraphs and hypographs further improves tightness and efficiency. The method is demonstrated to be particularly advantageous when dealing with activation functions like ReLU, as it provides exact representations of the upper bound which prior methods could only approximate. Overall, parametric relaxations provide a significant advancement, improving the efficiency and effectiveness of verifiable DNN editing by transforming a computationally intractable problem into an efficiently solvable linear program.
VNN-COMP Results#
The VNN-COMP (Verification of Neural Networks Competition) results section of a research paper would likely present a crucial evaluation of a proposed method for verifying or editing neural networks. It would compare the performance of the new method against existing state-of-the-art techniques on the standardized benchmarks provided by VNN-COMP. Key aspects to look for would include quantitative metrics such as accuracy, runtime, and the number of properties successfully verified or edited. The results should highlight the strengths and weaknesses of the proposed method compared to the baselines, especially concerning scalability and efficiency. A thorough analysis should be made regarding the types of neural networks and properties handled effectively. Statistical significance should be demonstrated to confirm that improvements aren’t merely due to chance. Finally, the limitations of the benchmark itself should be acknowledged, particularly if the benchmarks don’t fully represent the complexity of real-world applications. Overall, a strong VNN-COMP results section would provide convincing evidence of the effectiveness and efficiency of the new technique and help to place it within the broader landscape of DNN verification and editing research.
Robustness Editing#
Robustness editing, in the context of deep neural networks (DNNs), focuses on modifying a DNN’s parameters to enhance its resilience against adversarial attacks or noisy inputs. This is a crucial area of research because the vulnerability of DNNs to such perturbations can severely impact their reliability and safety in real-world applications. Effective robustness editing techniques must achieve a balance between improving robustness and preserving the model’s accuracy and efficiency. Current approaches often involve retraining or fine-tuning the DNN with specific loss functions or regularization methods designed to penalize deviations from desired properties. However, such methods might only provide empirical guarantees of robustness and are not always theoretically sound. A key challenge is creating provable editing techniques that provide rigorous mathematical guarantees. This requires efficient algorithms and sound verification techniques to ensure that the modified DNN satisfies desired robustness properties across all possible inputs within a defined region. Future work should explore the development of more efficient and provably correct robustness editing methods applicable to various DNN architectures and types of robustness properties (e.g., adversarial robustness, robustness to noise). Combining symbolic reasoning and numerical optimization techniques holds promise for advancing this field. Ultimately, the goal is to develop methods that make DNNs more reliable and trustworthy in safety-critical settings.
Future Directions#
Future research could explore extending PREPARED’s capabilities to handle more complex properties beyond simple interval bounds and local robustness, such as those involving temporal logic or intricate safety specifications. Investigating the scalability of PREPARED to even larger DNNs, particularly those with many layers and parameters, is crucial. This includes exploring techniques like compositional verification and efficient approximation methods. A key challenge will be developing more sophisticated techniques to handle non-linear activation functions, as the current linear relaxation approach might become too loose for some advanced architectures. Furthermore, research into integrating PREPARED with existing DNN verification tools would improve the workflow, enabling a seamless transition between verification, editing, and re-verification. Finally, applying PREPARED to diverse applications beyond image recognition and natural language processing, such as those involving control systems or robotics, would demonstrate its broader utility and impact.
More visual insights#
More on figures

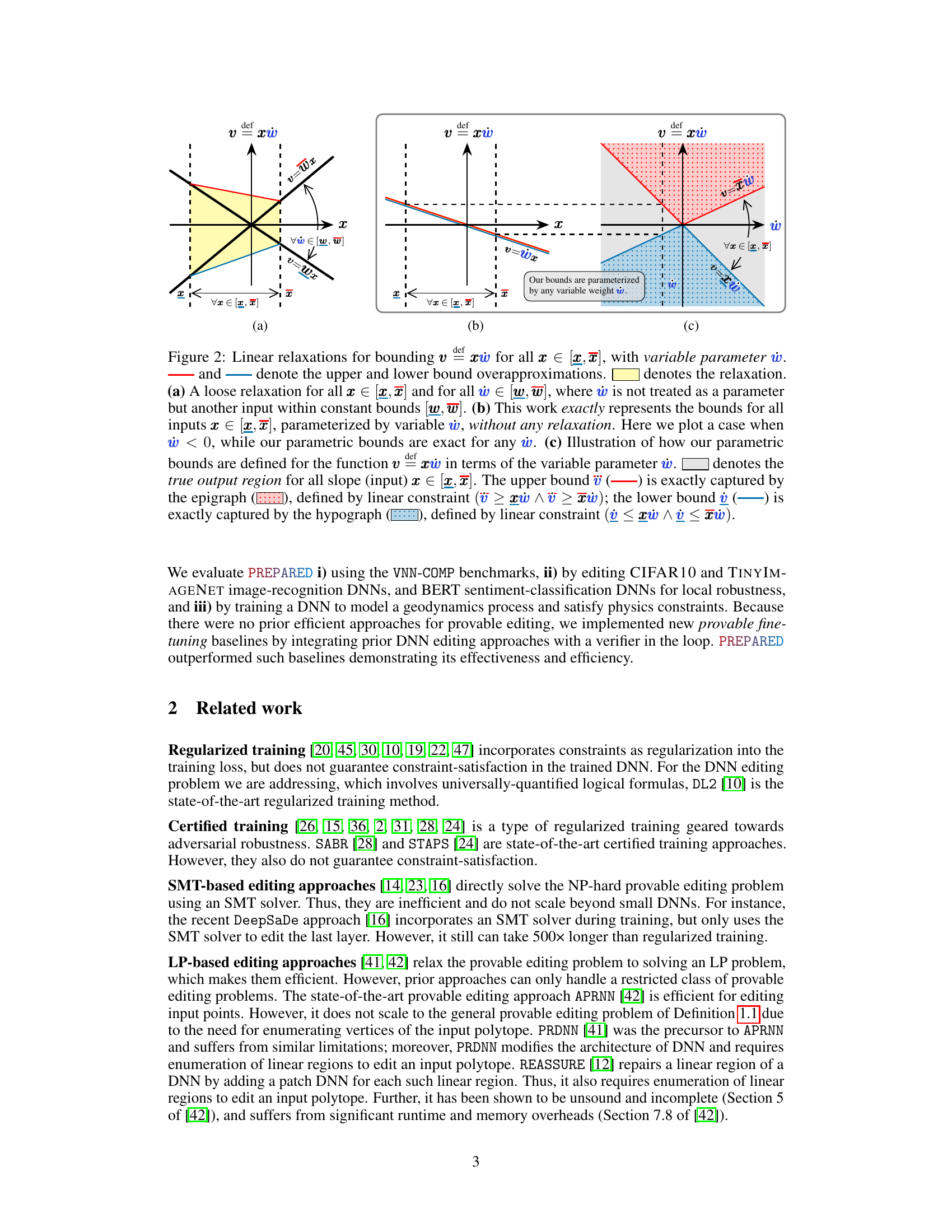
This figure illustrates three different linear relaxations for bounding v = xw, where w is a variable parameter. (a) shows a loose relaxation from prior work, which uses constant bounds for w. (b) shows the proposed method which provides exact bounds parameterized by w for all x ∈ [x, x]. (c) illustrates how the proposed method achieves this by capturing the epigraph and hypograph of the function.

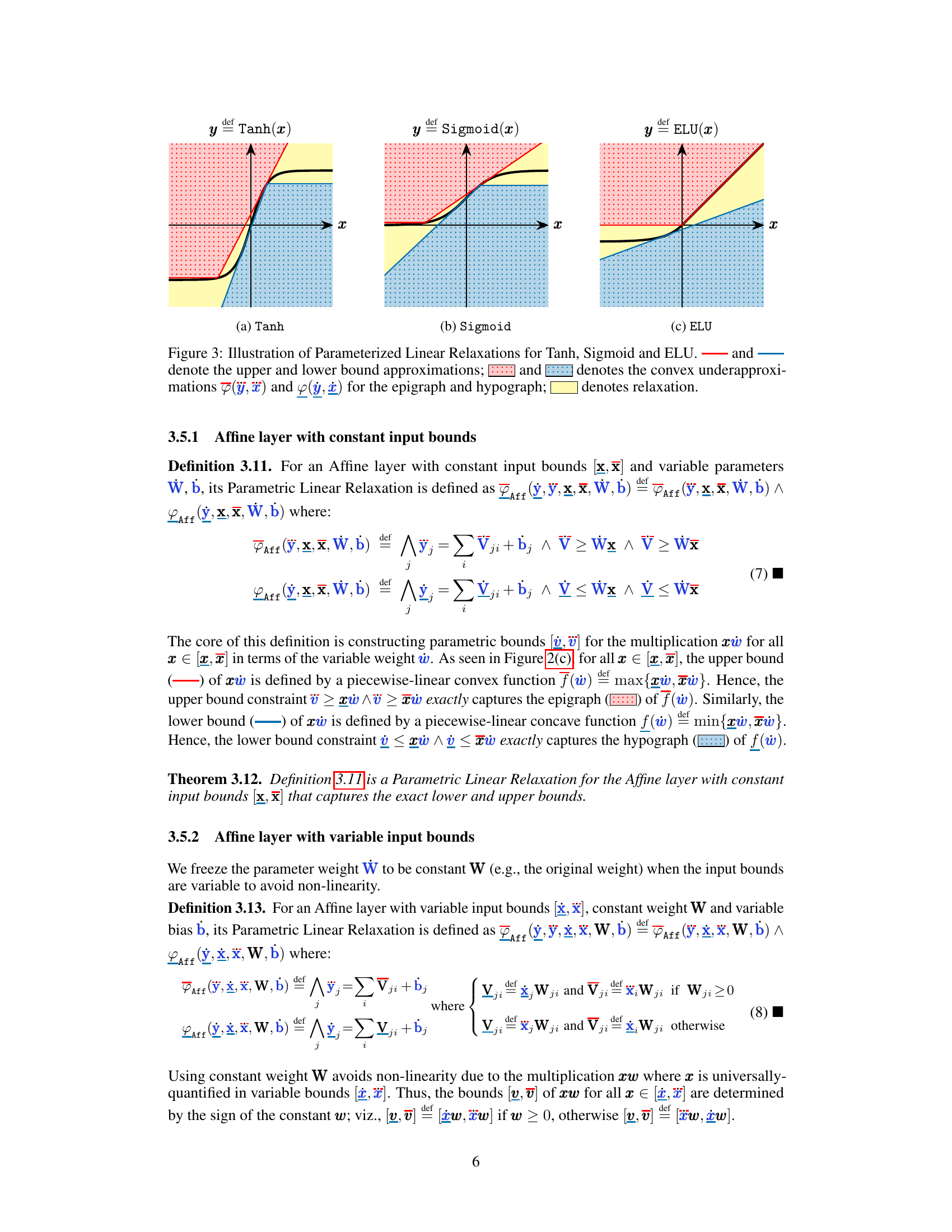
This figure shows the parameterized linear relaxations for Tanh, Sigmoid, and ELU activation functions. It illustrates how the approach constructs tight bounds for these functions by capturing their epigraph and hypograph using linear constraints, parameterized by the layer parameters, resulting in more precise approximations than prior approaches.
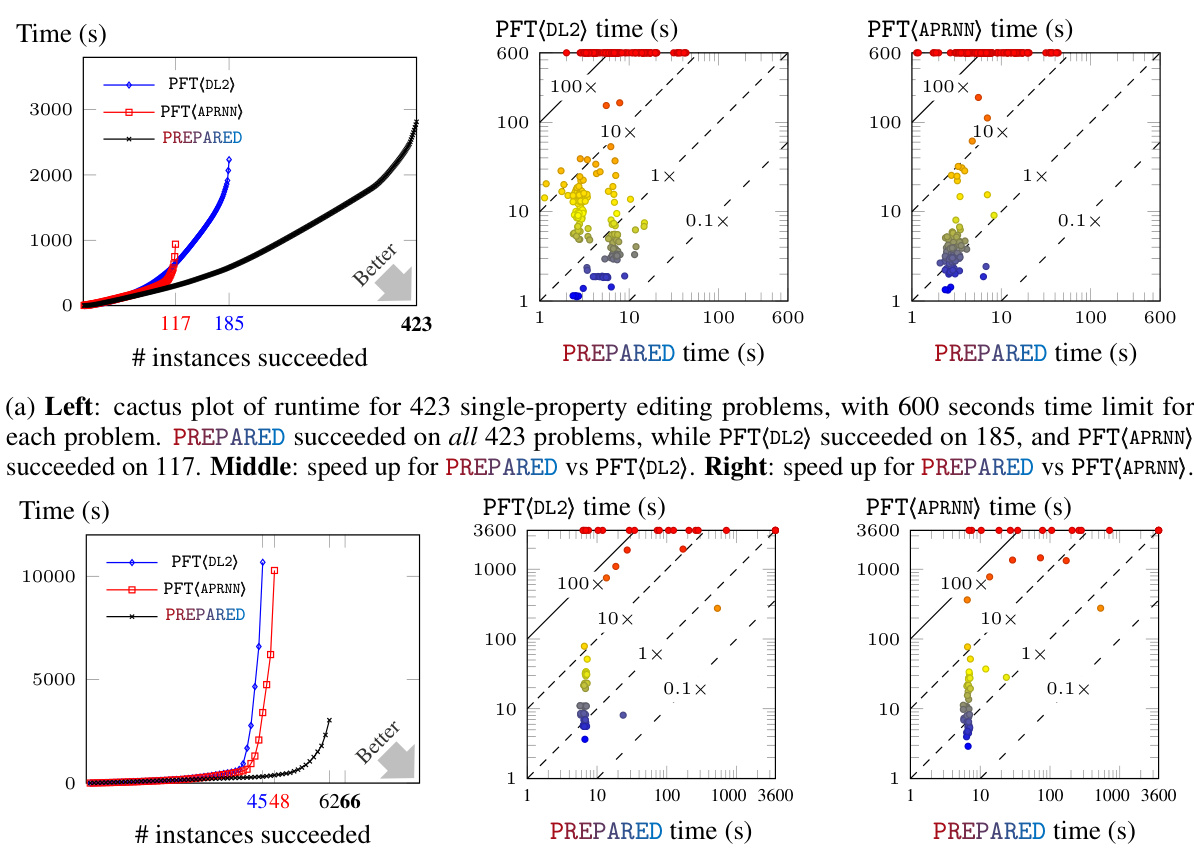
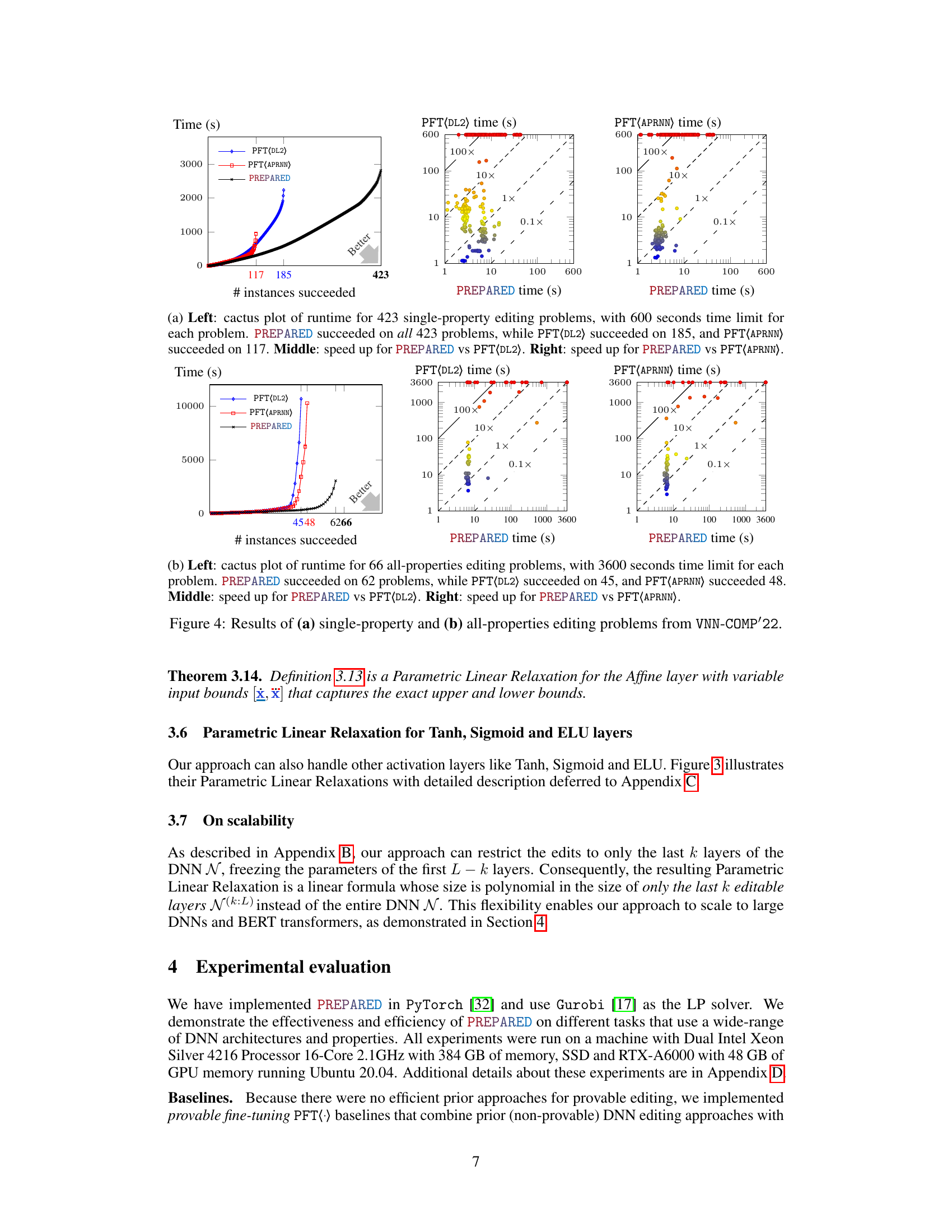
This figure presents the results of applying PREPARED and two baseline methods (PFT(DL2) and PFT(APRNN)) to solve single-property and all-properties editing problems from the VNN-COMP'22 benchmark. The plots show the runtime and success rate of each method. PREPARED significantly outperforms the baseline methods in both effectiveness and efficiency.
More on tables
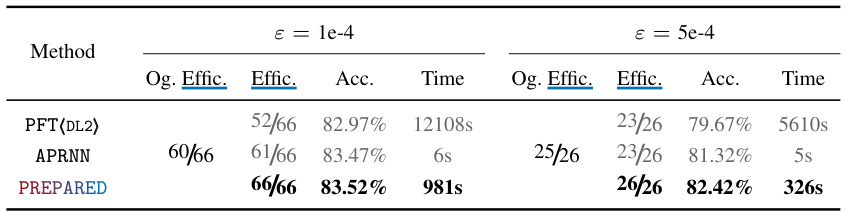
This table presents the results of local robustness editing experiments for sentiment classification using BERT transformers. It compares the performance of different methods (PFT(DL2), APRNN, and PREPARED) in terms of efficacy (percentage of successfully edited inputs), standard accuracy (overall accuracy), and runtime. Two different perturbation levels (epsilon) are tested. The original efficacy (Og. Effic.) before editing is included as a baseline. Rows where the efficacy is below 100% are highlighted to emphasize that the goal is to achieve perfect local robustness.
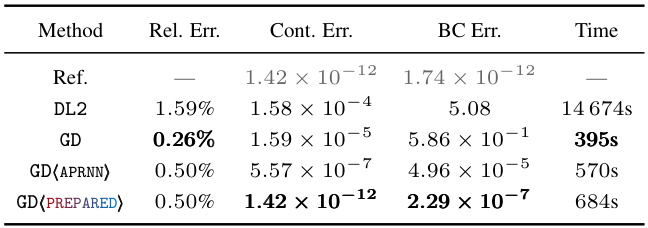
This table presents a comparison of different methods for repairing a geodynamic DNN to satisfy global physics properties. The methods compared are DL2, GD (vanilla gradient descent), GD(APRNN) and GD(PREPARED). The table shows the relative error, continuity error, boundary condition error, and training time for each method. The reference errors from the test set are included for comparison. The best results (lowest errors) are highlighted.
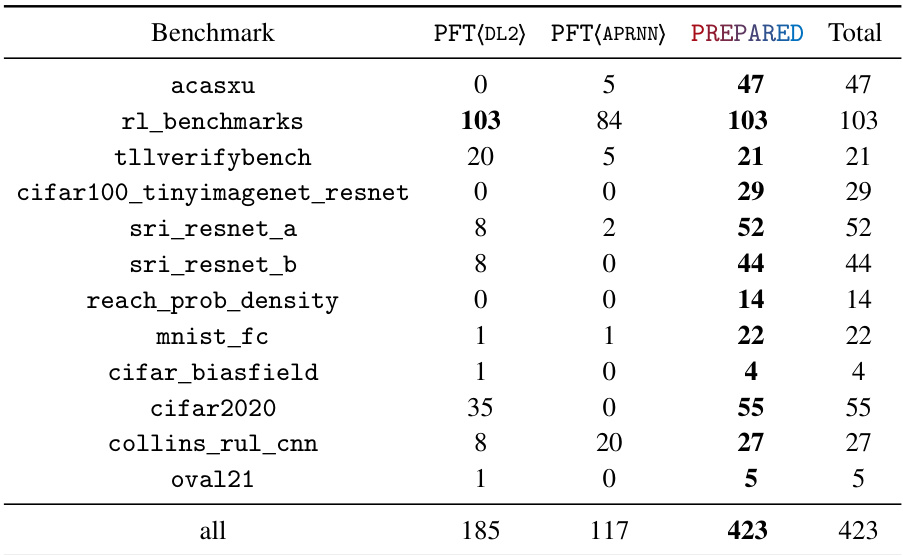
This table presents the results of comparing PREPARED against PFT(DL2) and PFT(APRNN) on VNN-COMP’22 benchmarks for two scenarios: single-property editing and all-properties editing. For single-property editing, it shows the number of successful edits for each benchmark using the three methods. For all-properties editing, it shows the same information, addressing the scenario of a DNN violating multiple properties simultaneously. The ‘Total’ column sums up successful instances across all benchmarks for each method.

This table presents the results of applying three different provable fine-tuning methods (PFT(DL2), PFT(APRNN), and PREPARED) to solve single-property and all-properties editing problems from the VNN-COMP'22 benchmark. It shows the number of successful edits for each method on various DNNs and properties, comparing their efficiency and effectiveness.
Full paper#