Piecewise deterministic generative models

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on generative models because it introduces a novel class of models based on piecewise deterministic Markov processes (PDMPs), offering scalability and efficiency advantages over diffusion-based models. The provided theoretical framework and training procedures will facilitate further research into PDMP-based generative models and their applications to various domains. It also opens up new avenues for exploring generative modeling in constrained or restricted domains, and on Riemannian manifolds.

Visual Insights

#

This figure displays three sample paths generated by three different piecewise deterministic Markov processes (PDMPs) used in the paper. The three processes are the Zig-Zag process (ZZP), the Bouncy Particle Sampler (BPS), and the Randomised Hamiltonian Monte Carlo (RHMC). Each plot shows the trajectory of the position vector of the particle in the process. The plots illustrate the different characteristics of these models, highlighting how they move deterministically between random jumps. The parameters used for generation are λ₁ = 1 and Tf = 10 for all three processes.

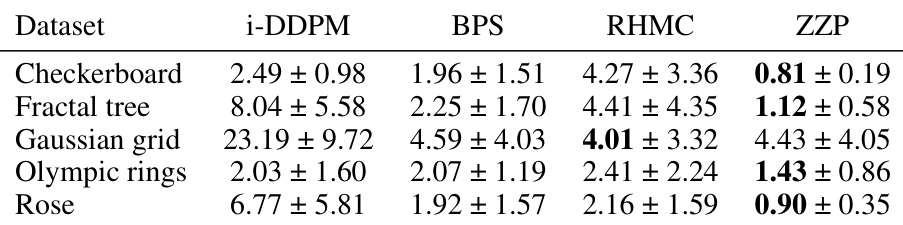
This table presents the results of evaluating the performance of different generative models on various datasets using the Kernel Maximum Mean Discrepancy (MMD) metric. Lower MMD values indicate better performance in generating samples similar to the real data. The table shows the average MMD scores and their standard deviations across six independent runs for each model and dataset. The datasets considered include: Checkerboard, Fractal tree, Gaussian grid, Olympic rings, and Rose. The models compared include i-DDPM, BPS, RHMC, and ZZP.

In-depth insights

#

PDMP Generative Models

#

The proposed “PDMP Generative Models” offer a novel approach to generative modeling by leveraging piecewise deterministic Markov processes (PDMPs). This contrasts with diffusion-based models, offering potential advantages in handling constrained domains and data distributions with both continuous and discrete components. The core idea is to characterize the time reversal of PDMPs, showing that they remain within the PDMP family, enabling the design of generative models that transition data from a simple base distribution to a complex target distribution. The paper likely details the application of this framework to specific PDMP types (Zig-Zag, Bouncy Particle Sampler, Randomized Hamiltonian Monte Carlo) and presents efficient training algorithms to learn the PDMP characteristics. Theoretical guarantees on the performance are likely provided, potentially through bounds on the total variation distance between the model’s generated distribution and the target data distribution. The efficacy of this method is likely evaluated on benchmark datasets, demonstrating its performance relative to existing state-of-the-art methods. A significant contribution would be the introduction of new generative models capable of handling complex data structures and geometries more effectively than existing diffusion-based approaches.

Time Reversal PDMPs

#

The concept of “Time Reversal PDMPs” presents a powerful technique for generative modeling by leveraging the properties of piecewise deterministic Markov processes (PDMPs). Time reversal, applied to PDMPs, creates a new PDMP with altered characteristics (jump rates and kernels) that are directly related to the conditional densities of the original process. This relationship enables the development of efficient training procedures to learn the parameters of the reversed PDMP. Crucially, the reversed PDMP bridges the data distribution and a simpler base distribution, mirroring the functionality of diffusion-based models. This approach holds significant promise, as PDMPs offer advantages over diffusion models, particularly when handling data residing in constrained spaces or manifolds. The methodology presented is novel and allows for the development of effective generative models based on a robust theoretical framework. Further investigation is needed into exploring the convergence properties of the learning procedures, particularly for high dimensional data, to fully realize the potential of time-reversed PDMP generative models.

Training & Inference

#

A hypothetical ‘Training & Inference’ section for a piecewise deterministic Markov process (PDMP)-based generative model would likely detail the two-stage training process. First, training the forward PDMP involves learning the parameters of the chosen PDMP (Zig-Zag, Bouncy Particle Sampler, or Random Hamiltonian Monte Carlo), potentially optimizing parameters via maximum likelihood estimation or score matching. Second, training the reverse PDMP necessitates approximating the backward process’s parameters using methods like ratio matching or normalizing flows, focusing on efficient estimation of conditional densities. Inference, then, would involve simulating the reverse PDMP from a simple base distribution, utilizing splitting schemes to efficiently approximate the stochastic process if exact simulation is computationally prohibitive. The overall success would hinge on the accuracy of the learned parameters for both the forward and reverse PDMPs, impacting the fidelity of generated samples.

Total Variation Bound

#

A total variation bound, in the context of generative models, quantifies the distance between the generated data distribution and the true data distribution. A smaller bound indicates that the generative model is a better approximation of the true distribution. This is crucial for evaluating the model’s performance and reliability. The derivation of such a bound often involves analyzing the properties of the underlying stochastic process used to generate the data, such as Markov processes or diffusion processes. The bound itself may depend on various factors including the model’s parameters, approximation errors and the time horizon considered. Tight bounds are highly desirable as they provide more confidence in the model’s accuracy, however obtaining such bounds can be computationally challenging. Understanding the components and limitations of the bound is key to effectively interpreting model performance and guiding further model development. The choice of metric, total variation distance, provides a robust measure of the discrepancy between probability distributions. Therefore, a comprehensive analysis of this bound offers significant insights into the quality and reliability of a generative model.

Future Research

#

Future research directions stemming from this piecewise deterministic generative model paper could involve several promising avenues. Extending the model to handle more complex data structures beyond simple toy examples and exploring its application to high-dimensional datasets like images and videos would be crucial. Improving the efficiency of the training procedures is also important; the current methods can be computationally expensive, especially for high-dimensional data. This might involve exploring alternative training strategies or leveraging more efficient architectures for the neural networks. Investigating the theoretical properties of the models in more detail, including rigorous convergence rates and bounds on generalization error, could lead to further improvements. Finally, a comprehensive comparison with state-of-the-art diffusion models across a wider range of datasets and evaluation metrics would provide a complete picture of its strengths and weaknesses.

More visual insights

#

More on figures

This figure compares the results of generating synthetic datasets using three different Piecewise Deterministic Markov Process (PDMP)-based generative models (ZZP, BPS, RHMC) and the improved denoising diffusion probabilistic model (i-DDPM). Each model is used to generate samples for two different datasets (Fractal tree and Olympic rings), and the visual results are shown for comparison. The figure demonstrates that PDMP-based models are able to capture finer details in the generated samples for these datasets.

This figure shows a comparison of the performance of different generative models (i-DDPM, BPS, RHMC, ZZP) on the Rose dataset in terms of Maximum Mean Discrepancy (MMD) and computational runtime. The x-axis represents the total computational time in milliseconds, and the y-axis shows the MMD score, a measure of the discrepancy between the generated and true data distributions. Lower MMD values indicate better performance. The plot reveals that the PDMP-based models (BPS, RHMC, ZZP) are generally faster and achieve lower MMD scores compared to i-DDPM, particularly when considering the computational time of generating samples with a given level of quality.

This figure compares the sample quality of RHMC and i-DDPM models for a small number of reverse steps (2 and 10). The top row shows results for a Gaussian grid dataset, while the bottom row shows results for a rose dataset. The goal is to visually demonstrate the relative performance of each model when using only a few reverse diffusion steps, highlighting how RHMC generates samples closer to the true data distribution in such scenarios.

This figure displays three plots showing sample paths for the position vector of three different piecewise deterministic Markov processes (PDMPs): the Zig-Zag process (ZZP), the Bouncy Particle Sampler (BPS), and the Randomised Hamiltonian Monte Carlo (RHMC). Each plot illustrates the trajectory of the particle’s position over time. The parameters λ₁ = 1 and Tf = 10 are consistent across all three processes. The plots provide a visual representation of the distinct dynamic behaviors of these PDMPs.

This figure compares the results of generating synthetic datasets using different methods: ZZP, BPS, RHMC, and i-DDPM. Each method generates samples for several two-dimensional datasets, and the visual comparison allows one to assess the quality of each method’s output. In particular, it seems to show that ZZP and BPS produce slightly more detailed results, compared to RHMC and i-DDPM.

This figure shows samples generated by a Zig-Zag Process (ZZP)-based generative model trained on the MNIST dataset. Each image is a generated digit, showcasing the model’s ability to produce handwritten digits similar to those in the training data.

More on tables

This table presents the results of the Maximum Mean Discrepancy (MMD) metric for different numbers of backward steps using four different generative models: i-DDPM, BPS, RHMC, and ZZP. The lower the MMD value, the better the model’s performance in generating samples that resemble the true data distribution. The table also shows the computational time per step for each model. The Rose dataset is one of several datasets used to evaluate the performance of the different models, which are all based on Piecewise Deterministic Markov Processes (PDMPs).

This table presents the results of comparing different generative models using the Kernel Maximum Mean Discrepancy (MMD) metric. The models compared are i-DDPM, and three piecewise deterministic Markov process (PDMP) based models: Zig-Zag Process (ZZP), Bouncy Particle Sampler (BPS), and Randomised Hamiltonian Monte Carlo (RHMC). The MMD values are averaged over six runs, and the standard deviations are also reported. Lower MMD scores indicate better performance.

This table summarizes the backward jump rates and kernels for three piecewise deterministic Markov processes (PDMPs): Zig-Zag process (ZZP), Randomised Hamiltonian Monte Carlo (RHMC), and Bouncy Particle Sampler (BPS). For each process, it shows how the backward jump rates and kernels are expressed in terms of the forward process’ conditional densities. These expressions are crucial for constructing the time-reversed PDMPs, which are fundamental to the generative modeling approach proposed in the paper.

This table presents the results of comparing the performance of different generative models (i-DDPM, ZZP, BPS, RHMC) on several datasets. The metric used is the Maximum Mean Discrepancy (MMD), which quantifies the difference between the generated data distribution and the true data distribution. Lower MMD values indicate better performance. The table shows the mean MMD and the corresponding standard deviation across six runs for each model and dataset. This allows for a statistical comparison of the different methods’ efficacy in generating data that closely matches the original data distributions.

This table presents the results of comparing the performance of different generative models, including the proposed Piecewise Deterministic Markov Process (PDMP) based models and the improved denoising diffusion probabilistic model (i-DDPM). The metric used is the Maximum Mean Discrepancy (MMD), which measures the difference between the data distribution and the distribution generated by each model. Lower MMD values indicate better performance. The table shows the average MMD and standard deviation across six runs for each model on five different datasets.

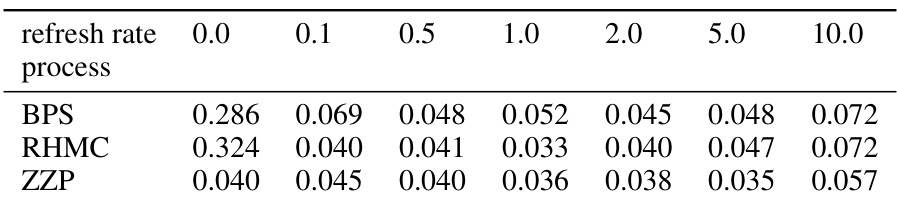
This table shows the mean 2-Wasserstein distances (W2) for different refresh rates (0.0, 0.1, 0.5, 1.0, 2.0, 5.0, 10.0) on a Gaussian grid dataset. The results are averaged over 10 runs for each of the three processes (BPS, RHMC, ZZP). Lower values indicate better performance.

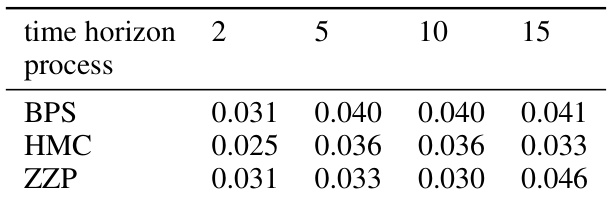
This table presents the mean 2-Wasserstein distances (W2) for different time horizons (2, 5, 10, 15) for three different piecewise deterministic Markov processes (BPS, HMC, ZZP). The results are averaged over 10 runs, and lower values indicate better performance of the generative models.

Full paper

#