TL;DR#
Diffusion models excel in generative modeling, especially behavior learning, but their iterative sampling process leads to long inference times, hindering real-time applications. Training Mixture of Experts (MoE) models, which offer faster inference, is notoriously difficult. This is due to the intractability of their likelihoods and their tendency towards mode-averaging during training.
This paper introduces Variational Diffusion Distillation (VDD), a novel method to overcome these challenges. VDD leverages variational inference to distill pre-trained diffusion policies into MoE models. A key innovation is the use of a decompositional upper bound of the variational objective, allowing for efficient, separate training of each expert. Experiments across nine complex behavior learning tasks demonstrate that VDD accurately distills complex distributions, surpasses existing methods, and sets a new benchmark for MoE training.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in robotics and machine learning due to its novel approach to distilling complex diffusion models, which are currently state-of-the-art in generative modeling, into more efficient and easily trainable Mixture of Experts (MoE) models. This addresses the challenges of long inference times and intractable likelihoods associated with diffusion models, opening new avenues for real-time applications such as robot control. The proposed method, Variational Diffusion Distillation (VDD), demonstrates superior performance compared to existing distillation techniques and traditional MoE training methods.
Visual Insights#
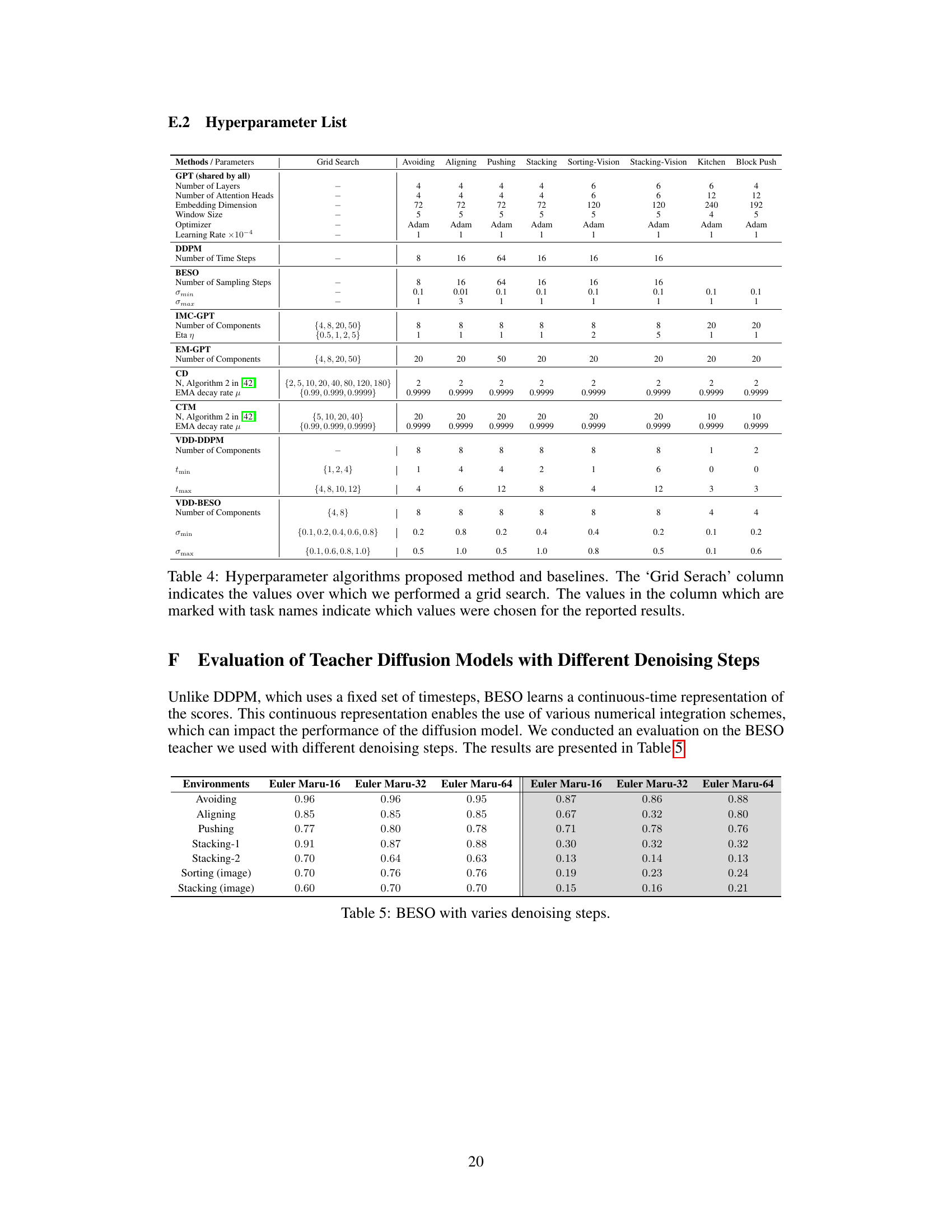
🔼 This figure illustrates the core idea of Variational Diffusion Distillation (VDD). The top panel shows how VDD distills a diffusion policy (which generates high-quality actions but is slow due to iterative sampling) into a Mixture of Experts (MoE) model using the score function. The bottom panel highlights the contrast between the iterative sampling process of a diffusion policy (red arrows) and the efficient single-step sampling of the MoE model produced by VDD. The figure uses the example of learning from human demonstrations (LfD) for robot control, where the inherent multimodality of human behavior makes it a challenging task.
read the caption
Figure 1: VDD distills a diffusion policy into an MoE. LfD is challenging due to the multimodality of human behaviour. For example, tele-operated demonstrations of an avoiding task often contain multiple solutions [13]. Lower: A diffusion policy can predict high quality actions but relies on an iterative sampling process from noise to data, shown as the red arrows. Upper: VDD uses the score function to distill a diffusion policy into an MoE, unifying the advantages of both approaches.

🔼 This table compares the performance of Variational Diffusion Distillation (VDD) against other state-of-the-art distillation methods (Consistency Distillation and Consistency Trajectory Model) and Mixture-of-Experts (MoE) training methods (Expectation-Maximization and Information Maximizing Curriculum) across nine behavior learning tasks. The metrics used are task success rate and task entropy. The table highlights VDD’s ability to achieve comparable performance to existing state-of-the-art while also exhibiting high versatility (high entropy).
read the caption
Table 1: Comparison of distillation performance, (a) VDD achieves on-par performance with Consistency Distillation (CD) (b) VDD is able to possess versatile skills (indicated by high task entropy) while keeping high success rate. The best results for distillation are bolded, and the highest values except origin models are underlined. In most tasks VDD achieves both high success rate and entropy. Note: to better compare the distillation performance, we report the performance of origin diffusion model, therefore only seed 0 results of diffusion models are presented here.
In-depth insights#
Diffusion Policy Distillation#
Diffusion policy distillation aims to transfer the capabilities of complex diffusion models to more efficient and tractable models, such as Mixture of Experts (MoE). Diffusion models excel at generating diverse and high-quality samples, but their iterative sampling process and intractable likelihoods limit their use in real-time applications. Distillation addresses this by learning a compact MoE policy that mimics the behavior of a pre-trained diffusion model. This involves a clever optimization scheme that leverages score functions, leading to robust training of the MoE. The resulting MoE policy retains the multi-modality and accuracy of the diffusion model while offering faster inference and a tractable likelihood, making it ideal for deployment in resource-constrained environments or real-time applications. A key challenge lies in effectively handling the multi-modal nature of diffusion models during distillation, but methods like variational inference offer a principled way to address this.
MoE Training#
Mixture of Experts (MoE) models offer the advantage of handling complex, multi-modal data distributions but pose challenges during training. Standard maximum likelihood objectives often lead to mode collapse or averaging, hindering the accurate representation of diverse data modes. This paper addresses these issues by introducing a novel variational inference framework for training MoEs. A key innovation is the decomposition of the variational objective into per-expert terms, enabling separate and robust optimization of each expert. This decompositional approach avoids the instability often associated with traditional MoE training methods. Further, the method leverages the gradients of a pre-trained diffusion model, effectively transferring the diffusion model’s knowledge of complex distributions to the MoE. The resulting training scheme is significantly more stable and produces superior results compared to existing MoE training techniques, showcasing the benefits of this variational distillation approach.
Variational Inference#
Variational inference is a powerful technique for approximating intractable probability distributions, particularly useful when dealing with complex models like those used in deep learning. It works by defining a simpler, tractable distribution (the variational distribution) that is close to the true, but complex, distribution of interest. The method then optimizes the parameters of the variational distribution to minimize the difference between it and the target distribution, often measured using the Kullback-Leibler (KL) divergence. This optimization process often involves iterative updates, balancing the tractability of the variational distribution with its accuracy in representing the true distribution. A key advantage is its scalability to large datasets and high-dimensional spaces, making it applicable to problems where exact inference is computationally infeasible. However, the success of variational inference depends heavily on the choice of the variational family and the accuracy of the approximation can vary significantly depending on the problem. Careful consideration of the variational family is crucial to ensure a good balance between tractability and accuracy of the approximation.
Ablation Studies#
Ablation studies systematically assess the impact of individual components within a model to understand their contributions. In the context of the described research, ablation studies likely involved removing or modifying parts of the variational diffusion distillation (VDD) method, such as the gating network, the number of experts, or the diffusion timestep selection method, and observing the effects on performance metrics. Key insights gained would center on understanding which components are crucial for achieving high accuracy, versatility, and efficiency. For example, removing the gating mechanism might reveal whether the model’s ability to handle multimodality stems from the expert selection process or from the expressiveness of the experts themselves. Similarly, experimenting with different numbers of experts might show an optimal trade-off between model complexity and performance. Investigating the influence of various timestep selection strategies would demonstrate whether one-step sampling can capture the key information or whether multi-step sampling is truly necessary to distill effectively. The results would guide future model improvements, demonstrating the essential design choices and enabling researchers to create a more streamlined and potentially more efficient model for complex tasks.
Future Work#
The authors suggest several promising avenues for future research. Improving training efficiency and enhancing performance are key goals. Leveraging the diffusion model as a backbone and fine-tuning an MoE head is proposed to reduce training time and potentially improve accuracy. Addressing the limitation of pre-defining the number of experts is also highlighted, suggesting that the model could benefit from dynamically adjusting the number of experts based on the task complexity. Finally, they acknowledge the need to investigate methods for applying VDD to high-dimensional data like images, requiring further investigation to overcome challenges posed by the MoE’s mean and covariance prediction. Extending VDD to real-world applications and exploring the effects of the diffusion model’s time-dependence to eliminate the need for the time-step selection scheme are also worthwhile future directions.
More visual insights#
More on figures

🔼 This figure demonstrates the VDD training process on a simple 2D example. Panel (a) shows the target probability distribution and its score function (gradients). Panels (b) through (f) show the iterative training process of the mixture of experts model (MoE), where each expert is represented by an orange circle. The training process gradually aligns the MoE components with the modes of the target distribution, avoiding overlaps.
read the caption
Figure 2: Illustration of training VDD using the score function for a fixed state in a 2D toy task. (a) The probability density of the distribution is depicted by the color map. The score function is shown by the gradient field, visualized as white arrows. From (b) to (f), we initialize and train VDD until convergence. We initialize 8 components, each represented by an orange circle. These components are driven by the score function to match the data distribution and avoid overlapping modes by utilizing the learning objective in Eq. (11). Eventually, they align with all data modes.

🔼 This figure presents ablation studies on several key design choices within the Variational Diffusion Distillation (VDD) method. Panel (a) shows how the number of experts impacts both task success rate and diversity, demonstrating a trade-off between these two metrics. Panels (b) and (c) compare the impact of training a gating distribution versus using a uniform distribution on task success and entropy, highlighting that training the gating distribution improves performance but reduces diversity. Finally, panel (d) examines the effect of sampling from multiple noise levels on the overall performance of VDD.
read the caption
Figure 3: Ablation studies for key design choices used in VDD. (a) Using only one expert leads to a higher success rate but is unable to solve the task in diverse manners. Sufficiently more experts can trade off task success and action diversities. (b)Learning the gating distribution improves the success rates in three D3IL tasks. (c) A Uniform gating leads to higher task entropy in two out of three tasks. (d) Sampling the score from multiple noise levels leads to a better distillation performance

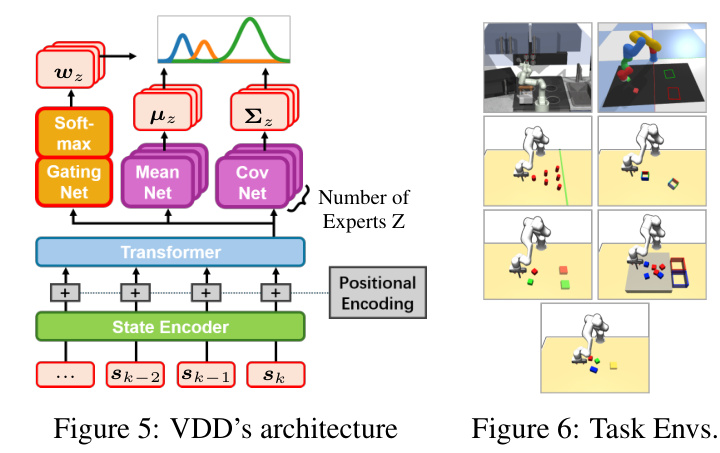
🔼 This figure visualizes the behavior of the VDD model on the ‘Avoiding’ task from the D3IL dataset for different numbers of experts (Z). The left panel shows the task environment. The main part of the figure shows trajectories generated by VDD with different numbers of experts. Different colors represent different experts, and their intensity reflects the probability of that expert being selected. The bottom row shows the individual experts’ behaviors. As the number of experts increases, the diversity of trajectories increases, showing VDD’s ability to capture multi-modal behaviors. With only one expert (Z=1), the behavior is deterministic, lacking the diversity seen in the teacher model.
read the caption
Figure 4: Trajectory visualization for VDD with different number of components Z ∈ {1,2, 4, 8} on the Avoiding task (left). Different colors indicate components with highest likelihood according to the learned gating network q(z|s) at a state s. For each step we select the action by first sampling an expert from the categorical gating distribution and then take the mean of the expert prediction. We decompose the case Z = 8 and visualize the individual experts zi (bottom row). Diverse behavior emerges as multiple actions are likely given the same state. For example, moving to the bottom right (21) and top right (22). An extreme case of losing diversity is seen with Z = 1, where the policy is unable to capture the diverse behavior of the diffusion teacher, leading to deterministic trajectories.

🔼 This figure illustrates the core idea of Variational Diffusion Distillation (VDD). The lower part shows how a diffusion policy generates actions through iterative sampling, which is slow. The upper part shows how VDD uses the score function of the diffusion model to distill the policy into a Mixture of Experts (MoE), resulting in a faster and more efficient model, especially beneficial for real-time applications like robot control.
read the caption
Figure 1: VDD distills a diffusion policy into an MoE. LfD is challenging due to the multimodality of human behaviour. For example, tele-operated demonstrations of an avoiding task often contain multiple solutions [13]. Lower: A diffusion policy can predict high quality actions but relies on an iterative sampling process from noise to data, shown as the red arrows. Upper: VDD uses the score function to distill a diffusion policy into an MoE, unifying the advantages of both approaches.
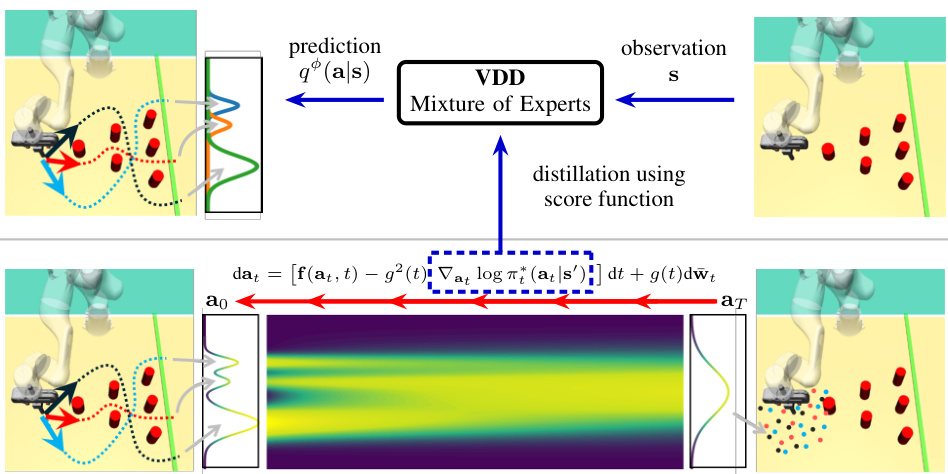
🔼 This figure illustrates the core idea of Variational Diffusion Distillation (VDD). The top part shows VDD transforming a complex diffusion policy (represented by the iterative sampling process from noise to data) into a simpler, faster Mixture of Experts (MoE) model. The bottom part highlights the challenge of learning from human demonstrations (LfD) due to the inherent multi-modality of human behavior, which diffusion models are well-suited to handle, but their iterative sampling makes real-time applications difficult. VDD addresses this by distilling the diffusion model’s knowledge into an MoE, combining the accuracy of diffusion models with the speed and tractability of MoEs.
read the caption
Figure 1: VDD distills a diffusion policy into an MoE. LfD is challenging due to the multimodality of human behaviour. For example, tele-operated demonstrations of an avoiding task often contain multiple solutions [13]. Lower: A diffusion policy can predict high quality actions but relies on an iterative sampling process from noise to data, shown as the red arrows. Upper: VDD uses the score function to distill a diffusion policy into an MoE, unifying the advantages of both approaches.

🔼 This figure illustrates the core concept of Variational Diffusion Distillation (VDD). The lower part shows how a diffusion policy generates actions through an iterative sampling process, which is computationally expensive. In contrast, the upper part illustrates how VDD distills the diffusion policy into a more efficient Mixture of Experts (MoE) model using the score function. This allows for faster action prediction and addresses the multimodality often found in human behavior data (LfD).
read the caption
Figure 1: VDD distills a diffusion policy into an MoE. LfD is challenging due to the multimodality of human behaviour. For example, tele-operated demonstrations of an avoiding task often contain multiple solutions [13]. Lower: A diffusion policy can predict high quality actions but relies on an iterative sampling process from noise to data, shown as the red arrows. Upper: VDD uses the score function to distill a diffusion policy into an MoE, unifying the advantages of both approaches.
More on tables

🔼 This table compares the performance of Variational Diffusion Distillation (VDD) against other state-of-the-art distillation methods (Consistency Distillation, Consistency Trajectory Model) and Mixture-of-Experts (MoE) training methods (Expectation-Maximization, Information Maximizing Curriculum) across nine different robotic manipulation tasks. The table shows task success rate and entropy for each method. The results demonstrate that VDD achieves comparable or better performance than existing methods while maintaining or improving the diversity of learned behaviors.
read the caption
Table 1: Comparison of distillation performance, (a) VDD achieves on-par performance with Consistency Distillation (CD) (b) VDD is able to possess versatile skills (indicated by high task entropy) while keeping high success rate. The best results for distillation are bolded, and the highest values except origin models are underlined. In most tasks VDD achieves both high success rate and entropy. Note: to better compare the distillation performance, we report the performance of origin diffusion model, therefore only seed 0 results of diffusion models are presented here.
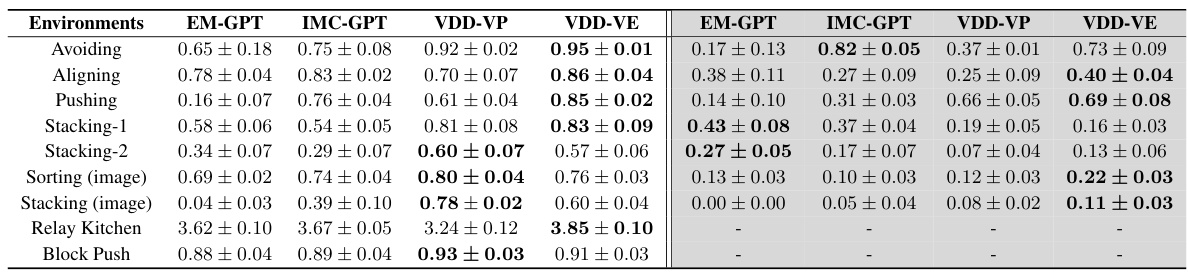
🔼 This table compares the performance of Variational Diffusion Distillation (VDD) against other state-of-the-art distillation methods (Consistency Distillation and Consistency Trajectory Model) and Mixture of Experts training methods (Expectation-Maximization and Information Maximizing Curriculum) across nine different robot manipulation tasks. The table shows success rates and entropy (measuring diversity of solutions) for each method. It highlights VDD’s ability to match or exceed the performance of other methods while also maintaining high solution diversity.
read the caption
Table 1: Comparison of distillation performance, (a) VDD achieves on-par performance with Consistency Distillation (CD) (b) VDD is able to possess versatile skills (indicated by high task entropy) while keeping high success rate. The best results for distillation are bolded, and the highest values except origin models are underlined. In most tasks VDD achieves both high success rate and entropy. Note: to better compare the distillation performance, we report the performance of origin diffusion model, therefore only seed 0 results of diffusion models are presented here.

🔼 This table compares the inference time of three different models: Variance Exploding (VE) BESO, Variance Preserving (VP) DDPM, and the proposed Variational Diffusion Distillation (VDD) method. Inference times are shown for different numbers of function evaluations (NFE), representing the number of steps in the diffusion process. The gray shaded area highlights the standard number of steps used in the original diffusion models.
read the caption
Table 3: Inference time in state-based pushing (left) and image-based stacking (right). The gray shaded area indicates the default setting for diffusion models.

🔼 This table compares the performance of Variational Diffusion Distillation (VDD) with other state-of-the-art distillation methods and the original diffusion models. The table is divided into two parts: (a) shows the task success rate or environment return (for the Kitchen task) and (b) shows task entropy. Higher task entropy indicates greater versatility of the learned behavior. The results demonstrate that VDD achieves comparable performance to state-of-the-art methods while achieving high task entropy in several tasks.
read the caption
Table 1: Comparison of distillation performance, (a) VDD achieves on-par performance with Consistency Distillation (CD) (b) VDD is able to possess versatile skills (indicated by high task entropy) while keeping high success rate. The best results for distillation are bolded, and the highest values except origin models are underlined. In most tasks VDD achieves both high success rate and entropy. Note: to better compare the distillation performance, we report the performance of origin diffusion model, therefore only seed 0 results of diffusion models are presented here.

🔼 This table compares the performance of Variational Diffusion Distillation (VDD) against other state-of-the-art distillation methods and the original diffusion models on various tasks. It shows success rates and entropy scores, highlighting that VDD achieves comparable performance while maintaining high versatility (entropy).
read the caption
Table 1: Comparison of distillation performance, (a) VDD achieves on-par performance with Consistency Distillation (CD) (b) VDD is able to possess versatile skills (indicated by high task entropy) while keeping high success rate. The best results for distillation are bolded, and the highest values except origin models are underlined. In most tasks VDD achieves both high success rate and entropy. Note: to better compare the distillation performance, we report the performance of origin diffusion model, therefore only seed 0 results of diffusion models are presented here.
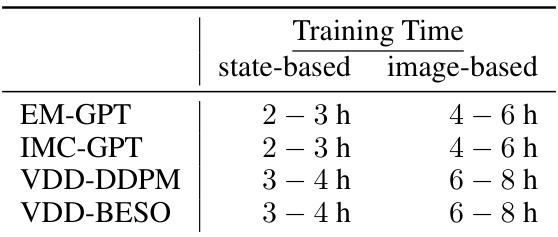
🔼 This table compares the performance of Variational Diffusion Distillation (VDD) against other state-of-the-art distillation methods and the original diffusion models across nine different tasks. It shows success rates and task entropy, highlighting VDD’s ability to achieve high performance and versatility while maintaining accuracy.
read the caption
Table 1: Comparison of distillation performance, (a) VDD achieves on-par performance with Consistency Distillation (CD) (b) VDD is able to possess versatile skills (indicated by high task entropy) while keeping high success rate. The best results for distillation are bolded, and the highest values except origin models are underlined. In most tasks VDD achieves both high success rate and entropy. Note: to better compare the distillation performance, we report the performance of origin diffusion model, therefore only seed 0 results of diffusion models are presented here.

🔼 This table compares the performance of Variational Diffusion Distillation (VDD) with other state-of-the-art distillation methods (Consistency Distillation (CD) and Consistency Trajectory Model (CTM)) and Mixture of Experts (MoE) training methods (EM-GPT and IMC-GPT) across nine different behavior learning tasks. It shows VDD achieves comparable success rate to CD, and in most cases outperforms other methods while also demonstrating higher task entropy (versatility) indicating diverse behavior solutions. The table shows success rate and entropy for each method.
read the caption
Table 1: Comparison of distillation performance, (a) VDD achieves on-par performance with Consistency Distillation (CD) (b) VDD is able to possess versatile skills (indicated by high task entropy) while keeping high success rate. The best results for distillation are bolded, and the highest values except origin models are underlined. In most tasks VDD achieves both high success rate and entropy. Note: to better compare the distillation performance, we report the performance of origin diffusion model, therefore only seed 0 results of diffusion models are presented here.
Full paper#