In-Context Learning with Representations: Contextual Generalization of Trained Transformers

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it provides the first theoretical proof demonstrating that transformers can learn contextual information to generalize to unseen examples and tasks, even with limited training data. This significantly advances our understanding of in-context learning, a key capability of large language models, and opens new avenues for improving model training and generalization.

Visual Insights

#

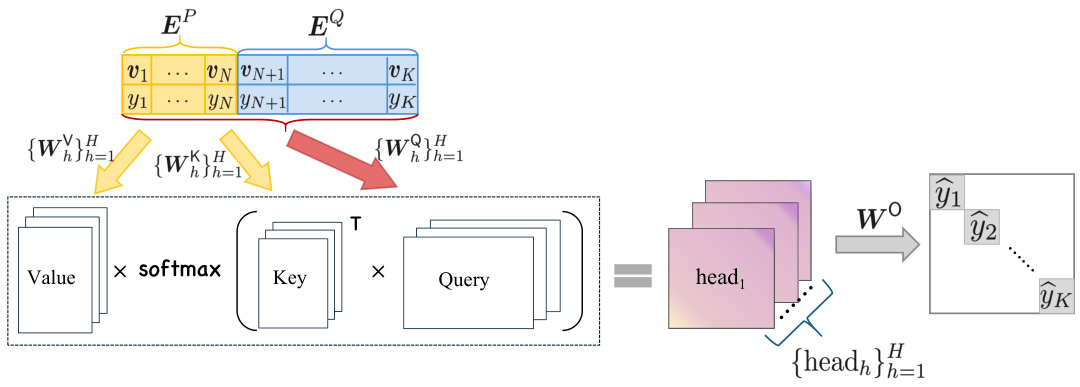
This figure shows the architecture of a one-layer transformer with multi-head softmax attention. The input consists of a prompt matrix E^P containing N query-answer pairs and a query matrix E^Q containing K-N unseen tokens. The prompt and query embeddings are processed through multi-head attention mechanism, where the query, key, and value matrices are W^Q, W^K, and W^V, respectively. The output is a prediction matrix ŷ containing K predicted labels for all tokens. The figure highlights the use of softmax function for attention weight calculation and multi-head attention for richer representation learning. The main processing steps involve query-key matrix multiplication, softmax normalization, value matrix multiplication, and the final linear transformation.

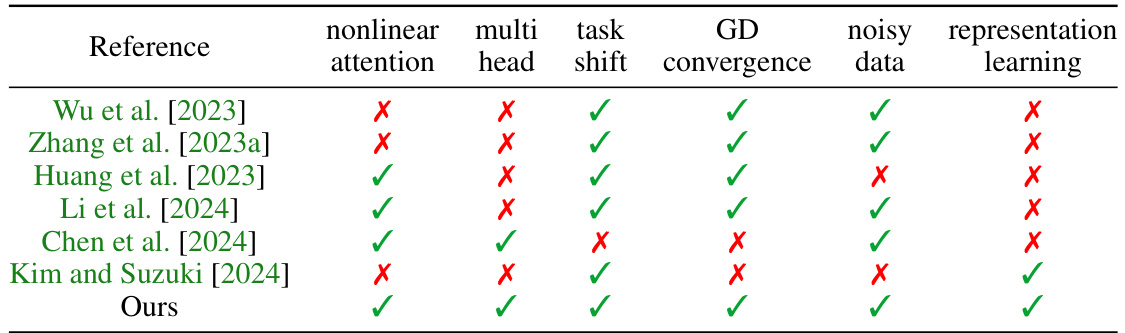
This table compares the current work with other theoretical studies on the learning dynamics of transformers in in-context learning (ICL). It contrasts various aspects of these studies, including whether they considered nonlinear attention mechanisms, multi-head attention, task shifting, gradient descent, noisy data, and whether the response variable was generated by a linearly weighted representation model. The table highlights the novel contributions of the current work by showing how it overcomes limitations of prior studies.

In-depth insights

#

ICL Representation

#

In exploring the concept of ‘ICL Representation’, a crucial aspect to consider is how in-context learning (ICL) leverages the internal representations of a language model to generalize to unseen tasks and examples. Understanding these representations is key to unlocking the mysteries of ICL’s success. Effective ICL relies on a model’s ability to discern patterns and relationships within the provided input examples to extrapolate solutions to novel scenarios. This involves complex processes within the model’s architecture that go beyond simple memorization; it’s about extracting relevant features and encoding them in a way that facilitates generalization. The dimensionality of these internal representations is significant. Higher dimensional spaces offer greater representational capacity, permitting the model to capture intricate nuances in language, leading to improved performance. However, excessively high dimensionality might introduce challenges in training and efficiency, raising questions about the optimal representation size. The dynamics of representation learning during ICL are also critical. How does the model’s internal representation evolve as it processes the examples? Does it adapt linearly, non-linearly, or through more complex mechanisms? This question highlights the need for further investigation into the training dynamics of ICL models to shed light on the underlying generalization capabilities.

Transformer Dynamics

#

Analyzing transformer dynamics offers crucial insights into their learning mechanisms. Understanding how internal representations evolve during training is key to explaining their remarkable in-context learning capabilities. Gradient descent’s role in shaping attention weights and internal feature representations needs careful examination. The interplay between model architecture (number of layers, attention heads), training data characteristics (size, noise), and optimization parameters directly affects the convergence speed and generalization performance. Research into these dynamics can reveal crucial information about a transformer’s bias, its ability to capture long-range dependencies, and its susceptibility to overfitting or underfitting. Furthermore, such analyses can shed light on the phenomenon of emergent capabilities, whereby transformers exhibit unexpected behaviors not explicitly programmed. By unveiling the hidden dynamics, we can improve model design, training strategies, and theoretical understanding, pushing the boundaries of what these powerful models can achieve.

Convergence Analysis

#

A rigorous convergence analysis is crucial for understanding the training dynamics of any machine learning model, especially deep neural networks. In the context of transformer-based models, convergence analysis typically involves demonstrating that the model’s training loss decreases monotonically and approaches a minimum value or a stable equilibrium. This analysis often requires making assumptions about the model architecture, data distribution, and optimization algorithm. For instance, analyses might focus on specific simplified architectures, such as single-layer or shallow transformers with simplified attention mechanisms, or assume specific data distributions like Gaussian noise or orthogonal feature vectors. The choice of optimization algorithm, such as gradient descent or variants like Adam, also significantly impacts the type of convergence analysis that can be performed. A successful convergence analysis typically establishes a convergence rate, indicating how quickly the loss function converges to its minimum. Linear convergence, for instance, is a desirable property indicating the loss decreases at a rate proportional to the current error. However, proving convergence for complex models like large language models remains a significant open challenge. Sophisticated mathematical tools and techniques, such as Lyapunov stability analysis or techniques from optimization theory, are often employed. The insights gained from a rigorous convergence analysis can provide a theoretical foundation for understanding why and how transformers are capable of learning complex patterns from data.

Generalization Bounds

#

Generalization bounds in machine learning aim to quantify the difference between a model’s performance on training data and its performance on unseen data. Tight bounds are crucial because they provide a measure of a model’s ability to generalize, which is the ultimate goal of machine learning. The derivation of such bounds often involves intricate statistical arguments, commonly employing techniques like Rademacher complexity, VC dimension, or covering numbers. These measures capture the model’s capacity to fit arbitrary functions, and the bounds relate this capacity to the generalization error. Factors like the model’s complexity, the size of the training dataset, and the noise in the data significantly influence the tightness and nature of these bounds. High complexity models tend to yield looser bounds, indicating a higher risk of overfitting. Conversely, larger datasets often lead to tighter bounds, implying more robust generalization. The presence of noise introduces uncertainty, potentially widening the gap between training and test performance and affecting the bound’s reliability. Improving our understanding and ability to derive tighter generalization bounds is a central research challenge because these bounds directly impact model selection, algorithm design, and our confidence in deploying machine learning models in real-world applications. In summary, while generalization bounds are theoretical constructs, they provide invaluable insights into practical aspects of model performance and predictive power.

Multi-head Attention

#

Multi-head attention is a crucial mechanism in modern transformer models, allowing them to attend to different parts of the input sequence simultaneously. Each head independently learns different aspects of the relationships between input elements. This is significantly more powerful than single-head attention, which can only focus on one type of relationship at a time. The use of multiple heads enables the model to capture a richer, more nuanced understanding of the context and relationships within the data. The independent learning of each head can be viewed as a form of parallelization, speeding up the processing and allowing for the identification of more complex patterns. In the context of in-context learning, multi-head attention is vital for the model to successfully learn contextual information from a limited number of examples. Each head may focus on a different aspect of the example, and the combination of these perspectives contributes to the model’s overall understanding. The number of heads is a hyperparameter that must be tuned for optimal performance; too few heads may limit the model’s capacity to capture complex relationships, while too many heads can increase computational cost and lead to overfitting. Research into the theoretical properties of multi-head attention, especially in the context of convergence and generalization, is an area of active research and is essential to advance our understanding of its effectiveness in various machine learning tasks.

More visual insights

#

More on figures

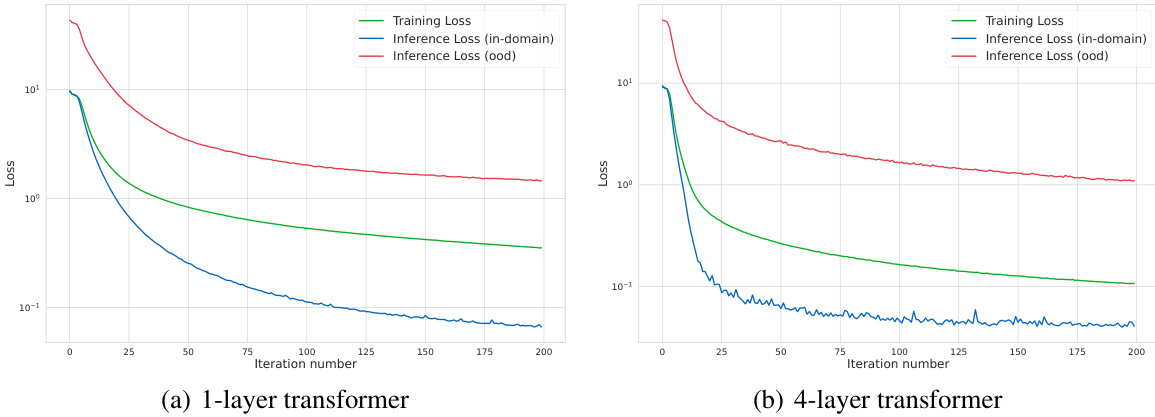
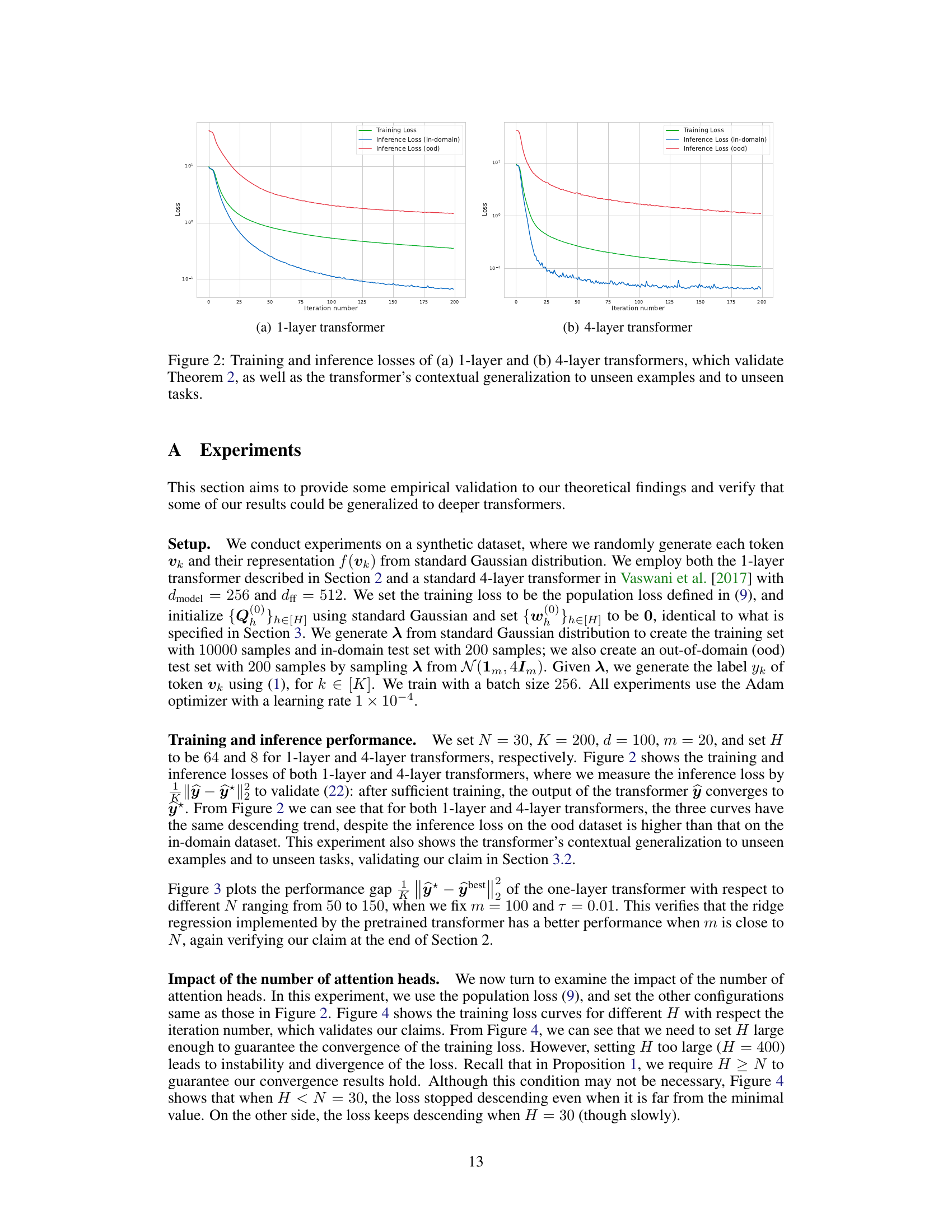
This figure shows the training and inference losses for both one-layer and four-layer transformers. The training loss curves show a clear downward trend indicating successful learning. The inference loss is measured both for in-domain (seen during training) and out-of-domain (unseen during training) examples. The results support Theorem 2 in the paper and demonstrate the model’s ability to generalize to both unseen examples and unseen tasks. Note that the out-of-domain inference loss is consistently higher than the in-domain inference loss, as expected.

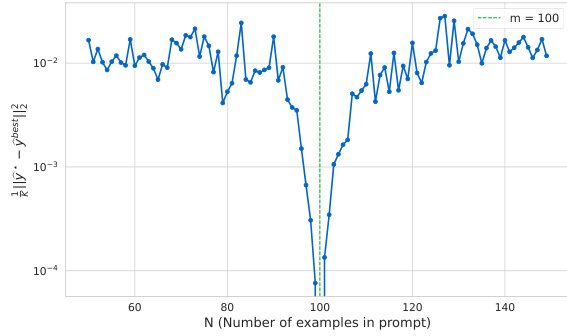
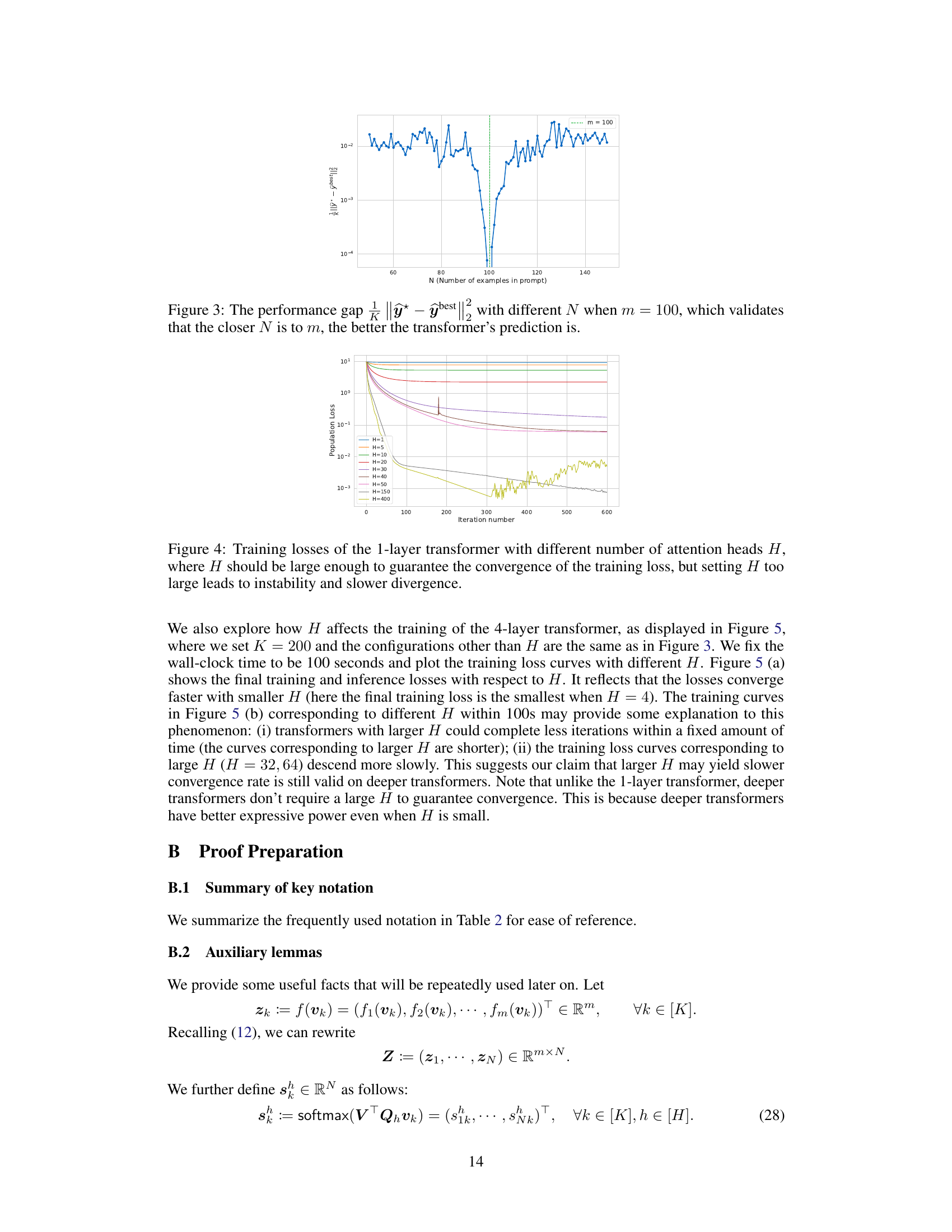
The figure shows the performance gap between the transformer’s prediction and the best possible prediction using ridge regression, plotted against the number of examples in the prompt (N). The vertical dashed line indicates when N equals m (number of basis functions). The plot shows that the performance gap is smallest when N is close to m, suggesting that the transformer’s performance improves as the number of examples in the prompt approaches the number of basis functions.

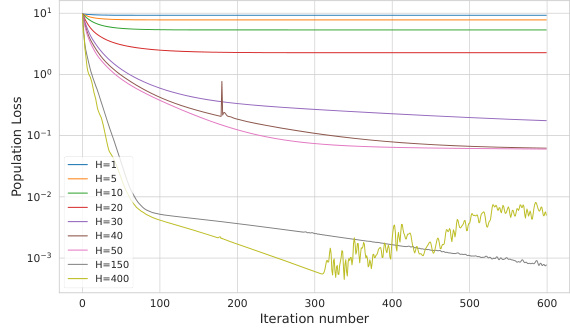
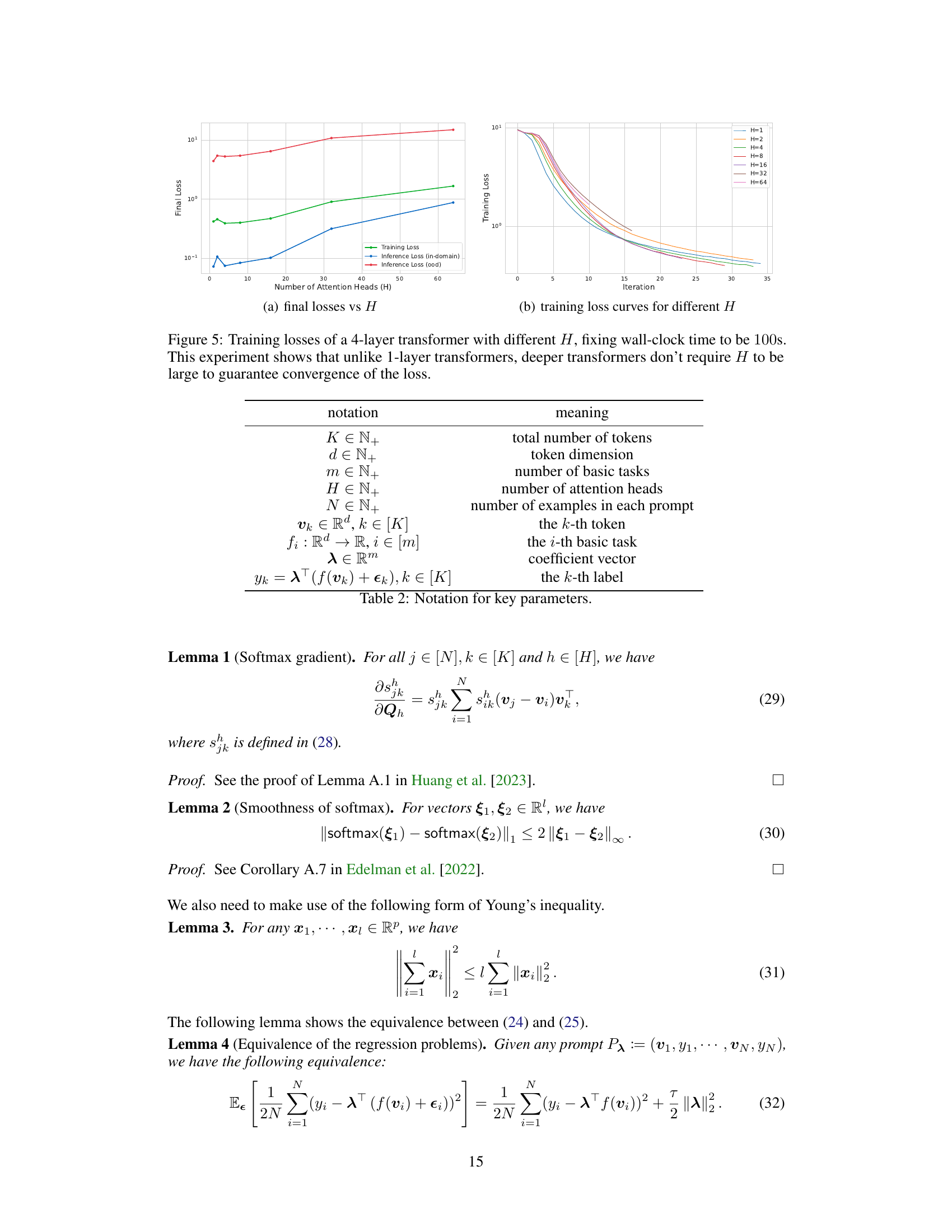
This figure shows how the number of attention heads (H) in a one-layer transformer affects its training performance. The x-axis represents the number of training iterations, and the y-axis shows the population loss. Multiple lines are plotted, each representing a different value of H. The results show that a small H leads to slower convergence, while too large an H leads to instability and divergence. There is an optimal range of H values for best training performance. This is consistent with the paper’s theoretical analysis demonstrating that the number of heads in the transformer affects its training and generalization performance.

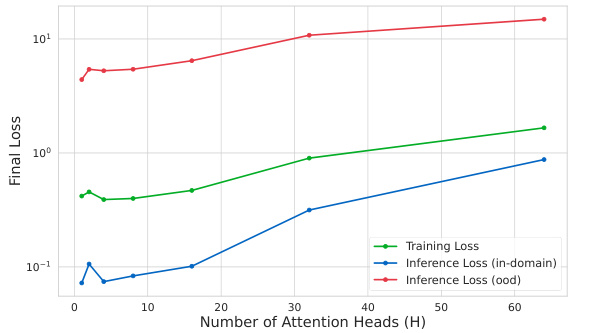
This figure shows the training losses for a one-layer transformer model with varying numbers of attention heads (H). The x-axis represents the number of attention heads, and the y-axis shows the final training loss after a fixed number of training iterations. The plot shows that a minimum number of attention heads is required to achieve convergence. However, using too many heads leads to instability and slower convergence. This highlights a trade-off between model capacity and training stability in the context of multi-head attention mechanisms.

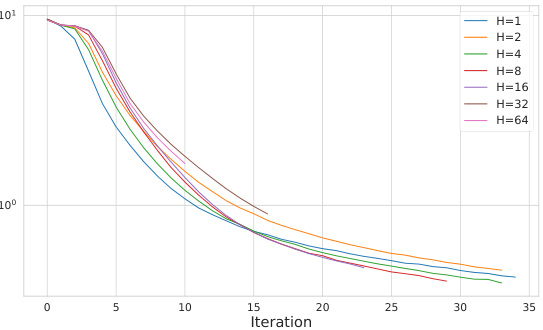
This figure shows how the number of attention heads (H) affects the training loss of a 4-layer transformer. It demonstrates that a sufficiently large H is needed for convergence, but excessively large values of H lead to instability and slower convergence. The experiment fixes the wall-clock time to 100 seconds and plots the training loss for different values of H, illustrating the trade-off between convergence speed and model stability.

Full paper

#