TL;DR#
Dynamic pricing, the art of setting optimal prices, is challenging when customer valuations depend on various factors (context). Existing methods often rely on strong assumptions about how these factors influence valuations, limiting their applicability. Also, they often yield suboptimal regret, a measure of how far the pricing strategy falls short of ideal revenue. This paper tackles these issues by focusing on two valuation models: one that assumes a linear relationship between context and valuation and another that is more general.
The paper introduces a new algorithm called VAPE (Valuation Approximation - Price Elimination) that intelligently estimates customer valuations and adapts prices accordingly. For the linear model, VAPE achieves an optimal regret bound, outperforming existing methods. For the more general model, it provides a new regret bound under very weak conditions, pushing the boundaries of dynamic pricing research. This implies improved revenue and pricing strategies with minimal assumptions.
Key Takeaways#
Why does it matter?#
This paper is important because it presents improved algorithms for contextual dynamic pricing, a crucial problem in revenue management. The optimal regret bounds achieved under minimal assumptions are significant theoretical contributions, advancing the field and offering practical guidance. The work opens new avenues for research in non-parametric settings and handling of non-i.i.d. contexts, driving innovation in personalized pricing strategies.
Visual Insights#
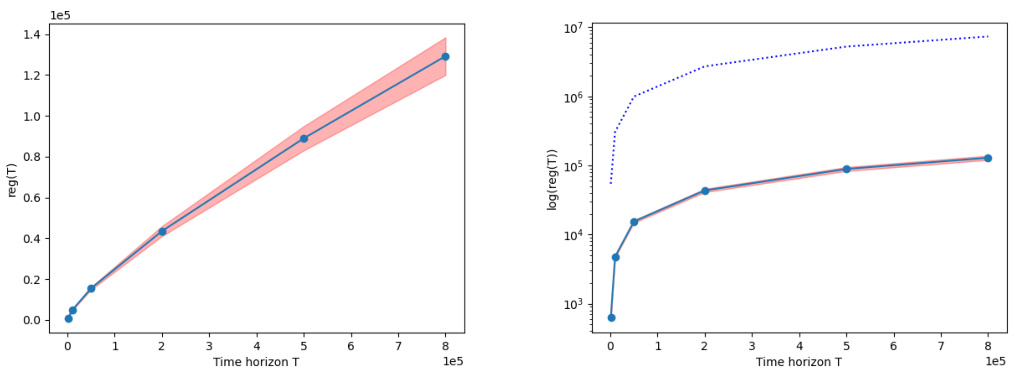
🔼 This figure displays the results of simulations evaluating the performance of the VAPE algorithm for linear valuations. The left panel shows the regret (the difference between the optimal revenue and the actual revenue obtained) against the time horizon (number of pricing decisions) on a linear scale. The right panel shows the same data but using a logarithmic scale for the y-axis (regret). The solid lines represent the average regret over 15 repetitions of the algorithm, while the shaded area represents the standard error. A dotted line in the right panel represents the theoretical regret bound derived from the theoretical analysis.
read the caption
Figure 1: The plots here show the regrets rate of VAPE for linear evaluations, both in the standard and logarithmic scale (left and right respectively). The solid lines represent the average of the performance over 15 repetitions of the routine. The faded red area shows the standard error, while in the right subplot the dotted line corresponds to the theoretical regret bound.
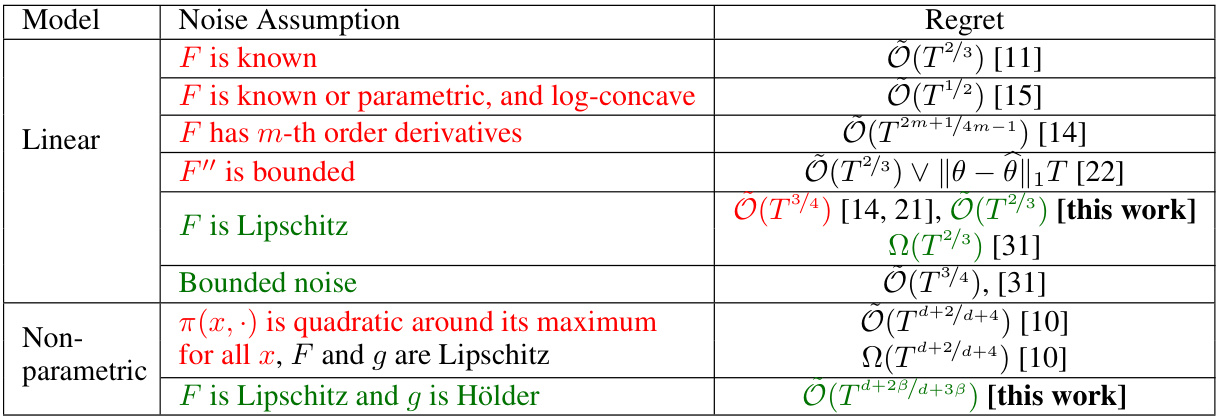
🔼 This table summarizes existing regret bounds from various research papers on dynamic pricing. It compares different models (linear and non-parametric) and assumptions about the noise distribution (e.g., known, parametric, Lipschitz continuous). The regret bounds represent the performance of different pricing algorithms, indicating how much revenue is lost compared to an optimal strategy.
read the caption
Table 1: Summary of existing regret bounds. g is the expected valuation function, F is the c.d.f. of the noise, and π(x, p) is the reward for price p and context x, defined in Section 2.1.
Full paper#



















