↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Offline model-based optimization (MBO) aims to find the best design using only pre-existing data, without the ability to test new designs. Existing methods often struggle due to limitations in learning highly multi-modal mappings and conservatism, making it difficult to find optimal solutions. Many methods focus on generating a single design from the data, limiting the potential for exploration of the design space. This hinders the ability to generate high-performing designs that lie beyond the scope of the initial dataset.
This paper introduces Guided Trajectory Generation (GTG), which tackles these problems by using a conditional diffusion model to generate a sequence of designs towards high-scoring regions. The model is trained on synthetic trajectories created from the original data by injecting locality bias for consistent improvement directions. By combining this trajectory generation with classifier-free guidance, GTG efficiently explores the design space and discovers high-scoring solutions, even beyond the original dataset. This novel approach significantly improves upon existing methods, setting a new standard for effectiveness in offline MBO.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a novel approach to offline model-based optimization (MBO), a crucial problem in many fields. The use of conditional diffusion models to generate high-fidelity designs offers a significant advancement over existing methods, and the demonstrated effectiveness on various benchmarks makes it highly relevant for researchers seeking efficient solutions to optimization problems where online evaluations are limited. The methodology could inspire further research on combining generative models and MBO techniques.
Visual Insights#

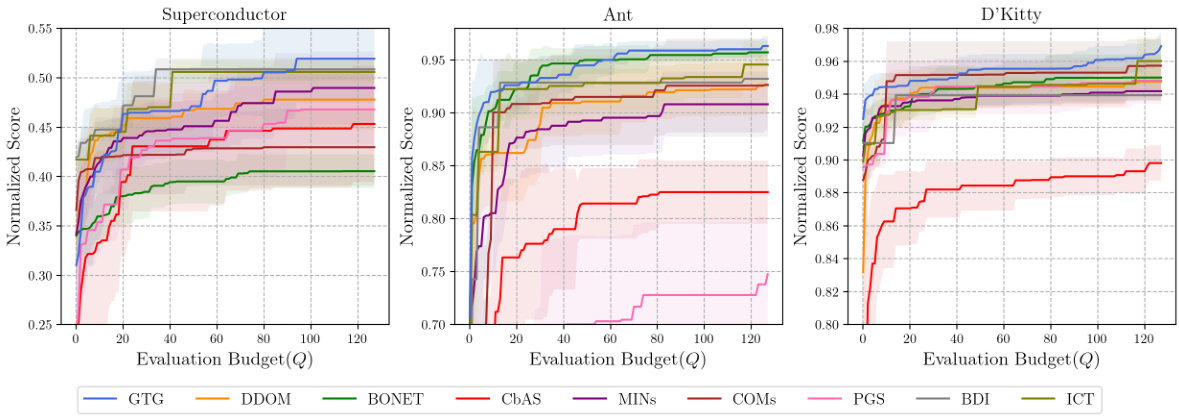
This figure shows a comparison of trajectory generation methods for offline model-based optimization. (a) shows trajectories generated by existing methods BONET and PGS which are not very diverse and do not effectively explore the design space. (b) shows trajectories generated by the proposed method GTG which are much more diverse and cover a wider range of the design space. (c) provides a detailed view of how GTG generates trajectories using a trained diffusion model, showing how context data points are used to guide the generation process.
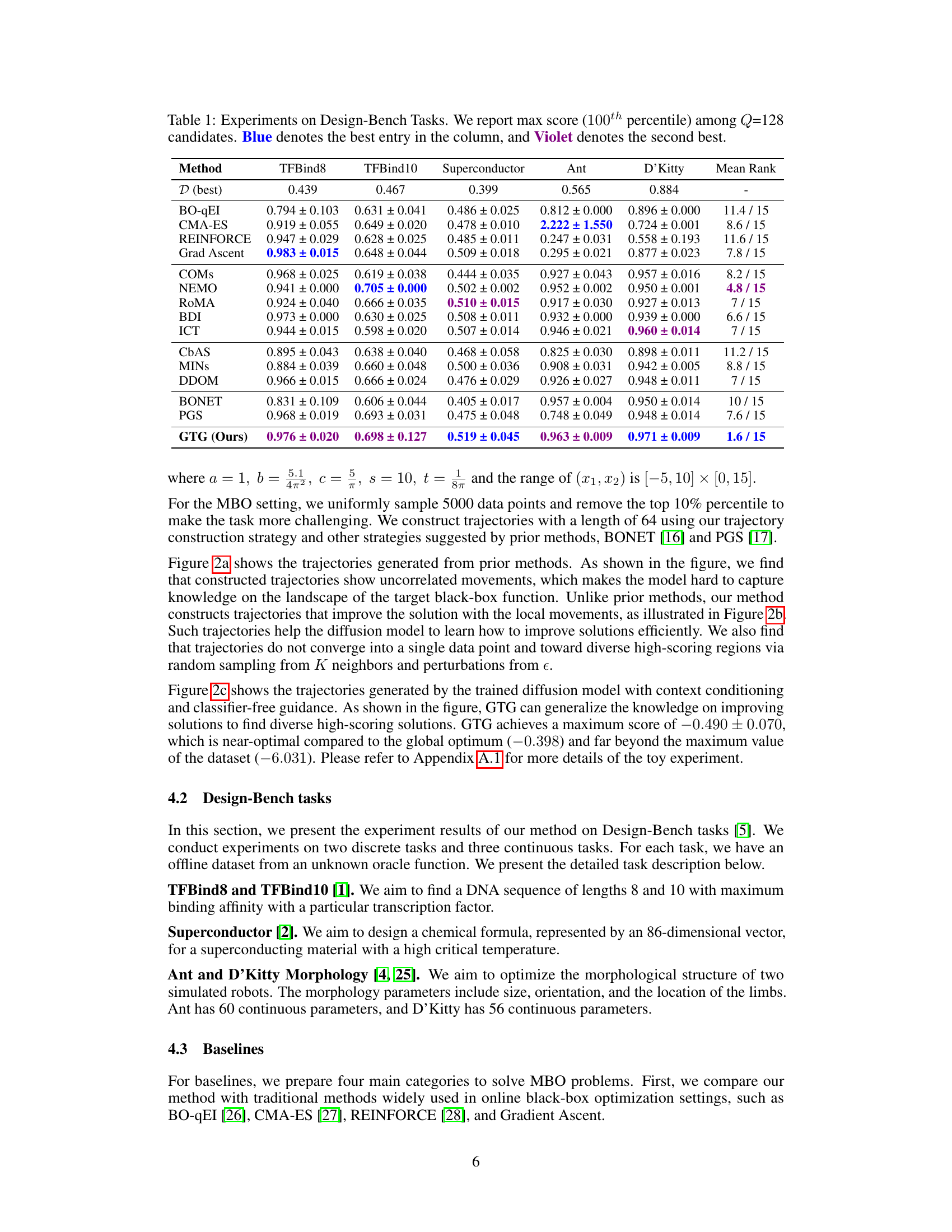
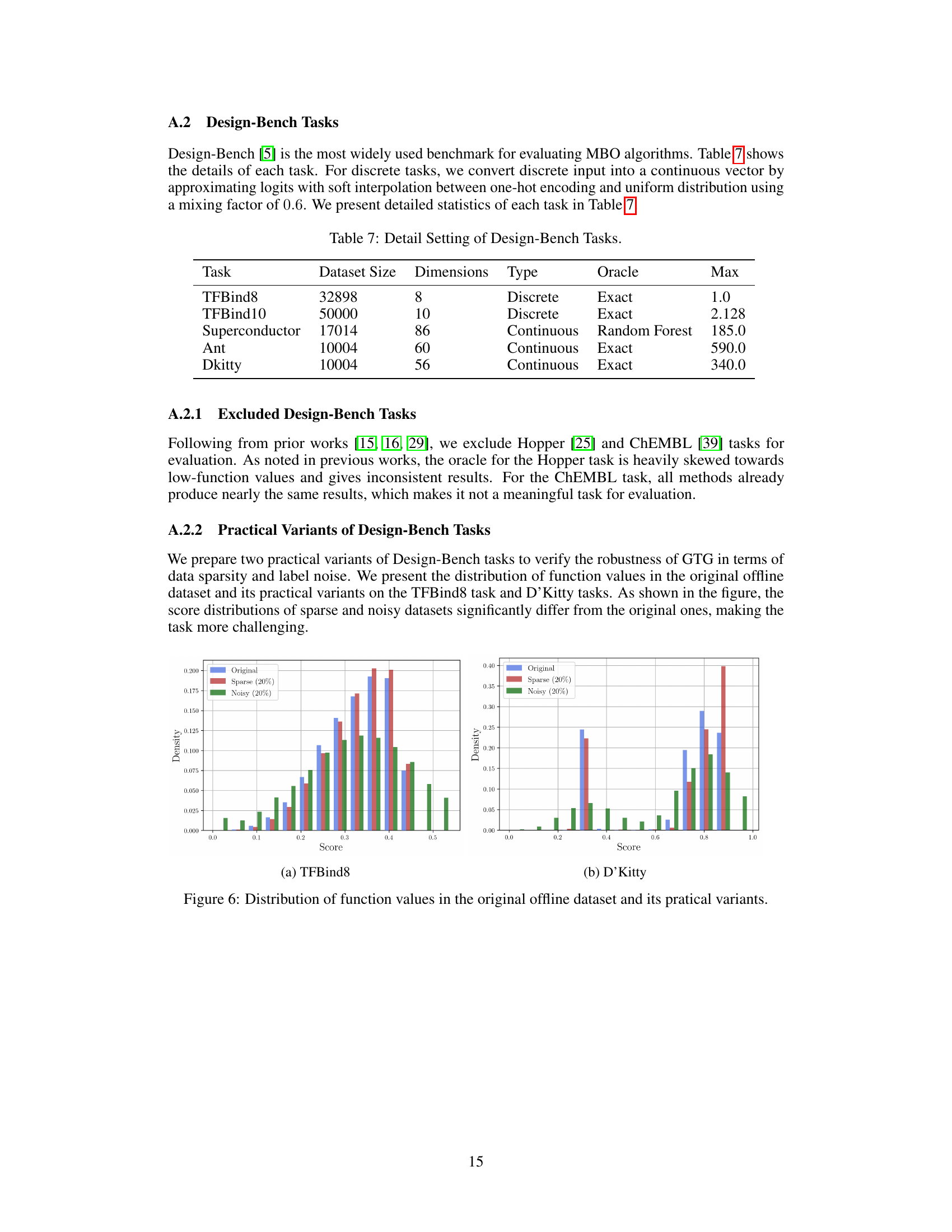
This table presents the results of experiments conducted on various tasks from the Design-Bench benchmark. For each task (TFBind8, TFBind10, Superconductor, Ant, D’Kitty), the table shows the maximum score achieved (100th percentile) among the top 128 candidate designs selected by each method. The scores are reported as mean ± standard error. The best and second-best results for each task are highlighted in blue and violet, respectively. The methods compared include various offline model-based optimization (MBO) approaches, allowing for a comparison of the relative performance of different techniques on these tasks.
In-depth insights#
Offline MBO Methods#
Offline model-based optimization (MBO) tackles the challenge of maximizing a black-box function using only pre-existing data, without the luxury of online evaluations. Several methods exist, each with strengths and weaknesses. Forward methods typically train a robust surrogate model to predict function values, often incorporating techniques to handle uncertainty in unseen regions. However, these can suffer from conservatism and struggle with highly multi-modal functions. Inverse methods, conversely, learn a mapping from function values to designs. While potentially more flexible, they can be hampered by the difficulty of modeling complex, non-smooth distributions. A recent, promising approach focuses on generating synthetic trajectories towards high-scoring regions from the offline dataset. This allows for exploration beyond the limited data, but the design of effective trajectory generation strategies remains crucial. Ultimately, the choice of offline MBO method depends heavily on the specific characteristics of the target function and dataset; no single approach is universally superior.
Diffusion Model Use#
The application of diffusion models in research papers often revolves around generative tasks, leveraging their ability to create high-quality samples from complex data distributions. A common use is generating synthetic data, particularly useful when real data is scarce, expensive to collect, or contains privacy concerns. This generated data can augment existing datasets, improving the performance of downstream machine learning models. Conditional diffusion models allow for more control over the generation process, enabling the creation of samples with specific properties. Moreover, diffusion models find use in inverse problem settings, where the goal is to infer input parameters from observed outputs. By learning the inverse mapping implicitly, these models can directly generate designs satisfying desired constraints. Finally, the denoising capability of diffusion models allows their use in data cleaning or enhancing noisy datasets, improving data quality and subsequent analysis. In all these scenarios, the strength of diffusion models is their capacity to model intricate probability distributions, and their effectiveness depends heavily on proper model architecture and training strategies.
Trajectory Generation#
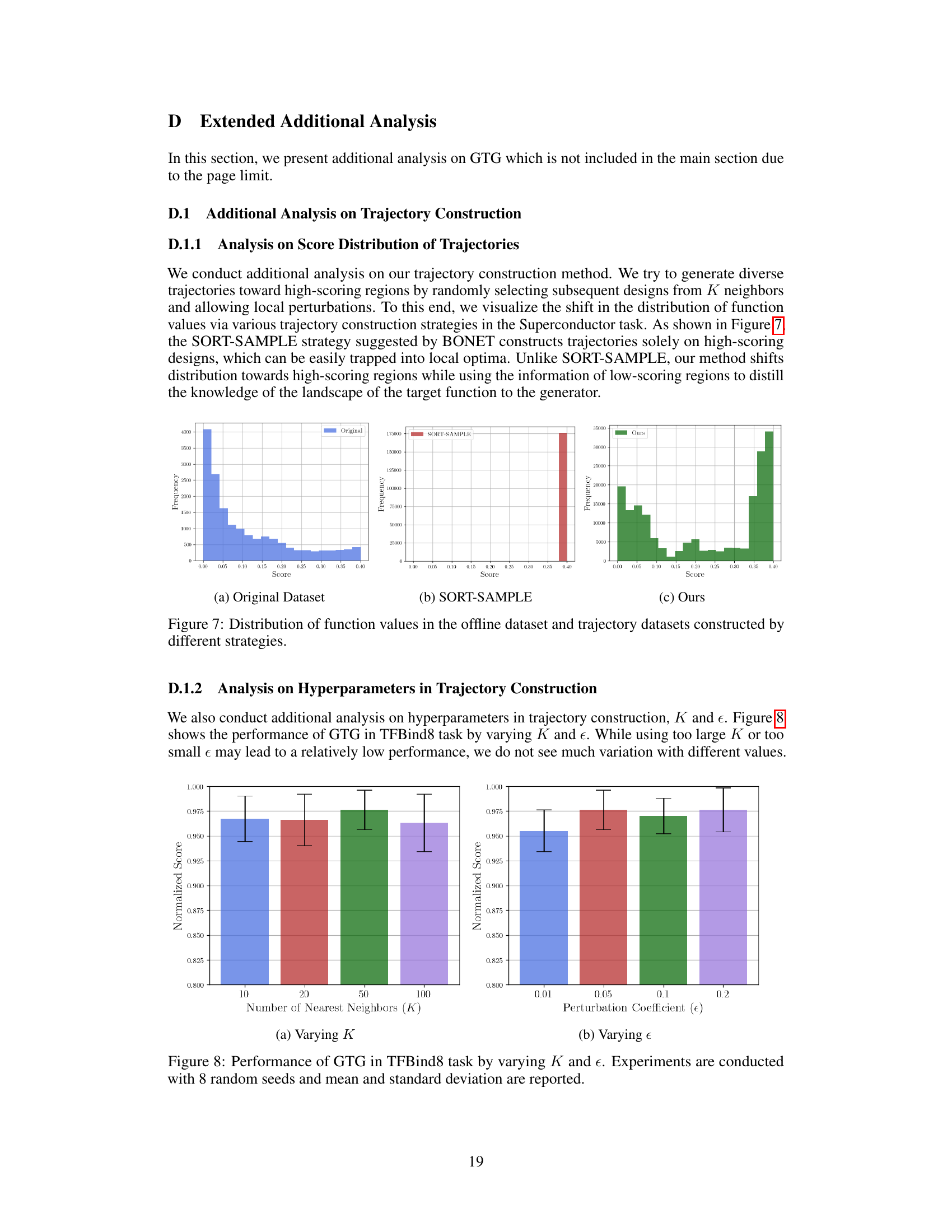
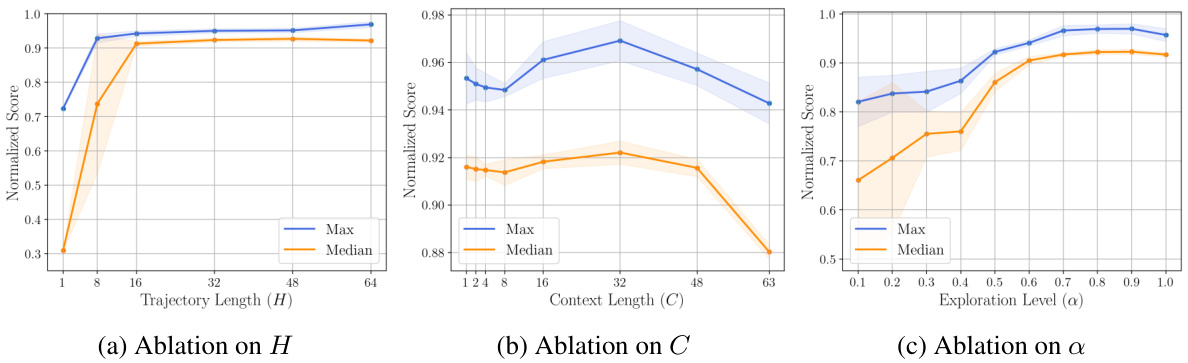
Trajectory generation, in the context of offline model-based optimization, is a crucial step in leveraging existing datasets to discover improved solutions. Effective trajectory generation methods must balance exploration and exploitation, guiding the search towards high-scoring regions while ensuring sufficient diversity to avoid premature convergence. The choice of generative model significantly impacts the quality of generated trajectories; diffusion models show promise due to their ability to capture complex, multi-modal distributions. Incorporating locality bias in trajectory construction improves consistency and efficiency, focusing improvement efforts along promising directions. Further enhancing performance involves incorporating techniques like classifier-free guidance and context conditioning. Classifier-free guidance promotes exploration beyond the training data, while context conditioning leverages existing data to contextualize the generated trajectories. The selection of high-fidelity designs from the generated trajectories requires careful consideration, often involving filtering via a robust proxy model. The interplay between trajectory generation, model selection, and filtering strategies is critical for achieving state-of-the-art performance in offline model-based optimization.
GTG Algorithm Details#
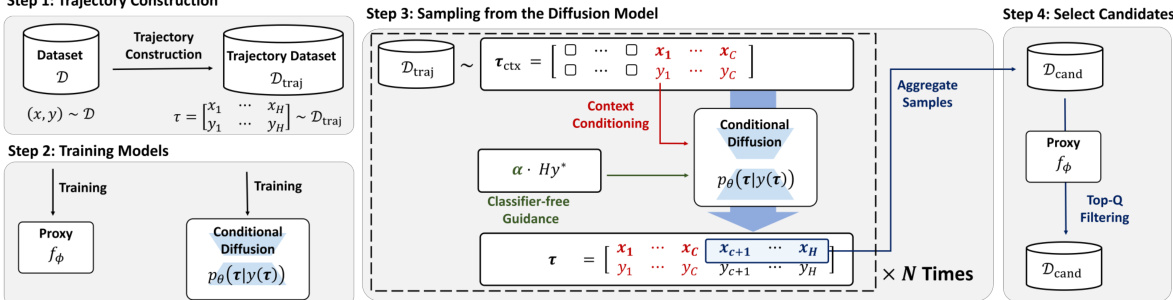
A hypothetical ‘GTG Algorithm Details’ section would delve into the intricate workings of the Guided Trajectory Generation algorithm. It would likely begin by formally defining the algorithm’s inputs and outputs, clarifying the role of the offline dataset in initializing trajectories. Crucially, a detailed explanation of trajectory construction would be essential, outlining how locality bias is injected to ensure consistent improvement directions and how high-scoring regions are targeted. The training procedures for both the conditional diffusion model and the proxy function would be meticulously described, specifying the loss functions, optimization techniques, and hyperparameter choices. The sampling process, a core component of GTG, would be dissected, outlining the mechanics of classifier-free guidance and context conditioning, and explaining how this approach facilitates exploration beyond the initial dataset. Finally, candidate selection would be elaborated, detailing how the proxy model filters trajectories to identify high-fidelity designs. A comprehensive explanation of the algorithm’s computational complexity would enhance the section, offering insights into the algorithm’s scalability and practical applicability. The inclusion of visualizations and pseudocode would aid in understanding and allow for easier reproduction of the results.
Future Work#
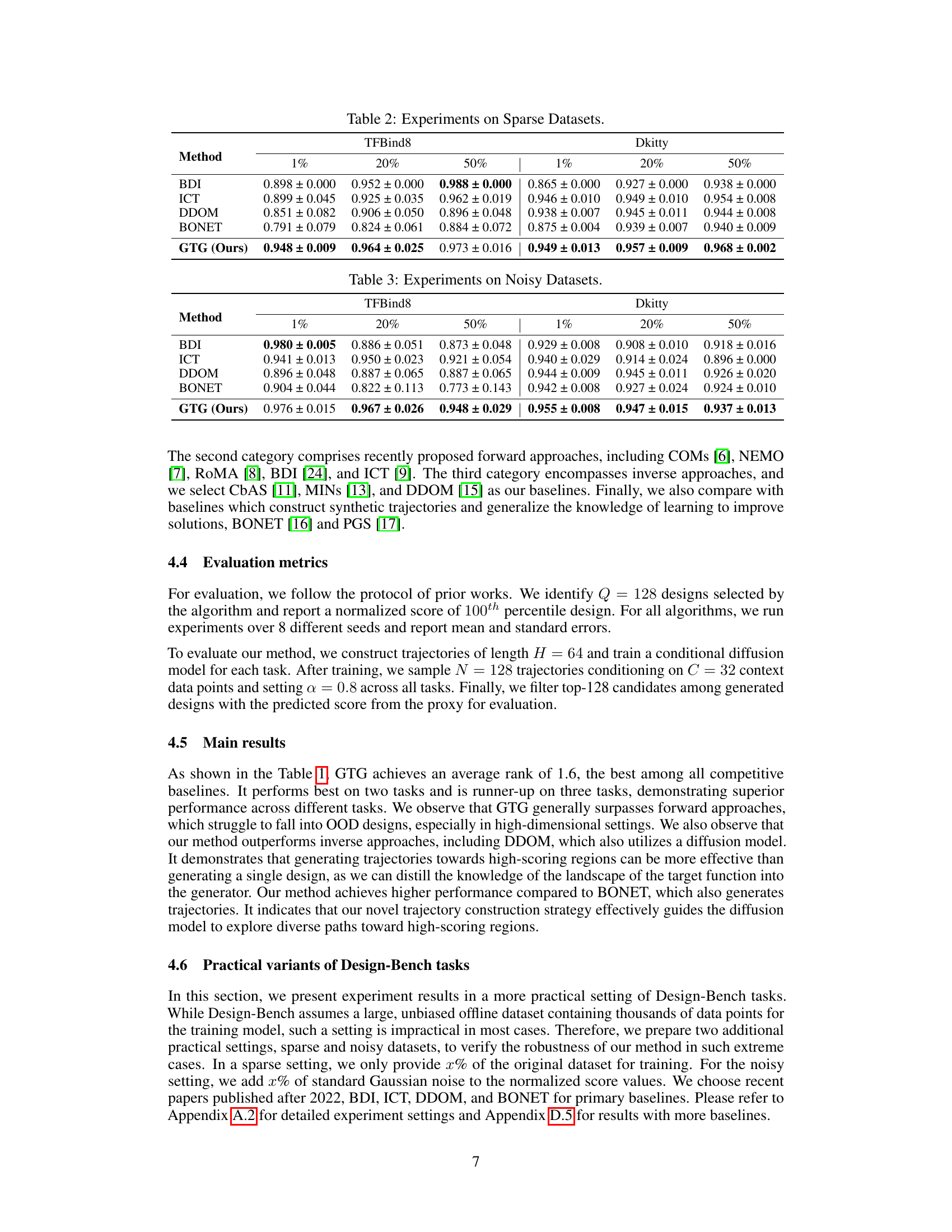
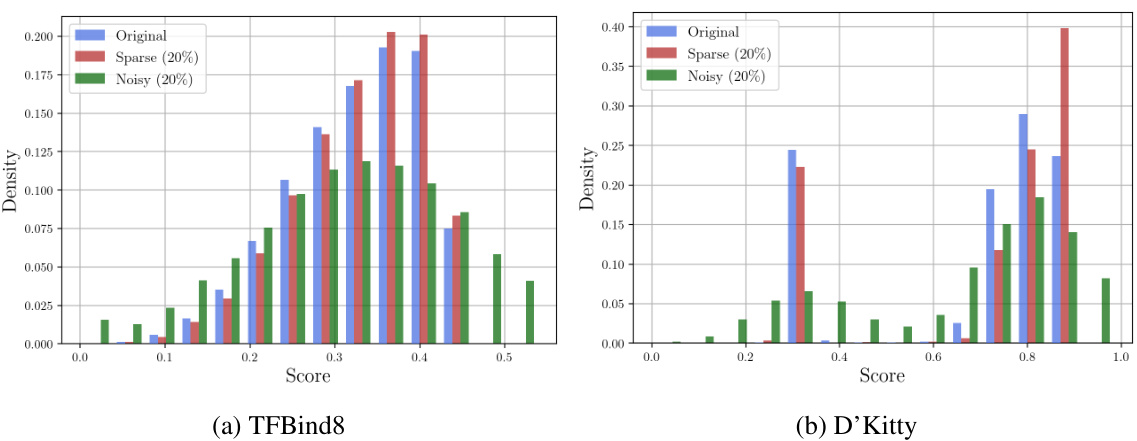
Future work in offline model-based optimization (MBO) could explore several promising directions. Improving the robustness of proxy models is crucial, as inaccurate predictions severely limit performance, especially in out-of-distribution regions. More sophisticated trajectory generation methods are needed to better capture the landscape of complex, high-dimensional functions, potentially leveraging advanced generative models or reinforcement learning techniques. Incorporating uncertainty quantification into trajectory generation and design selection is key to balancing exploration and exploitation. Finally, addressing the challenges of sparse and noisy datasets remains an important research avenue, requiring strategies to effectively leverage limited or unreliable data. Investigating the applicability of GTG to a wider range of real-world problems and exploring alternative objective functions beyond maximization would also be valuable future research avenues.
More visual insights#
More on figures
This figure provides a visual overview of the Guided Trajectory Generation (GTG) method proposed in the paper. It outlines the four main steps involved: 1) constructing trajectories from the offline dataset, 2) training a conditional diffusion model and a proxy function, 3) sampling trajectories using classifier-free guidance and context conditioning, and 4) selecting high-fidelity candidates for evaluation using the proxy function.
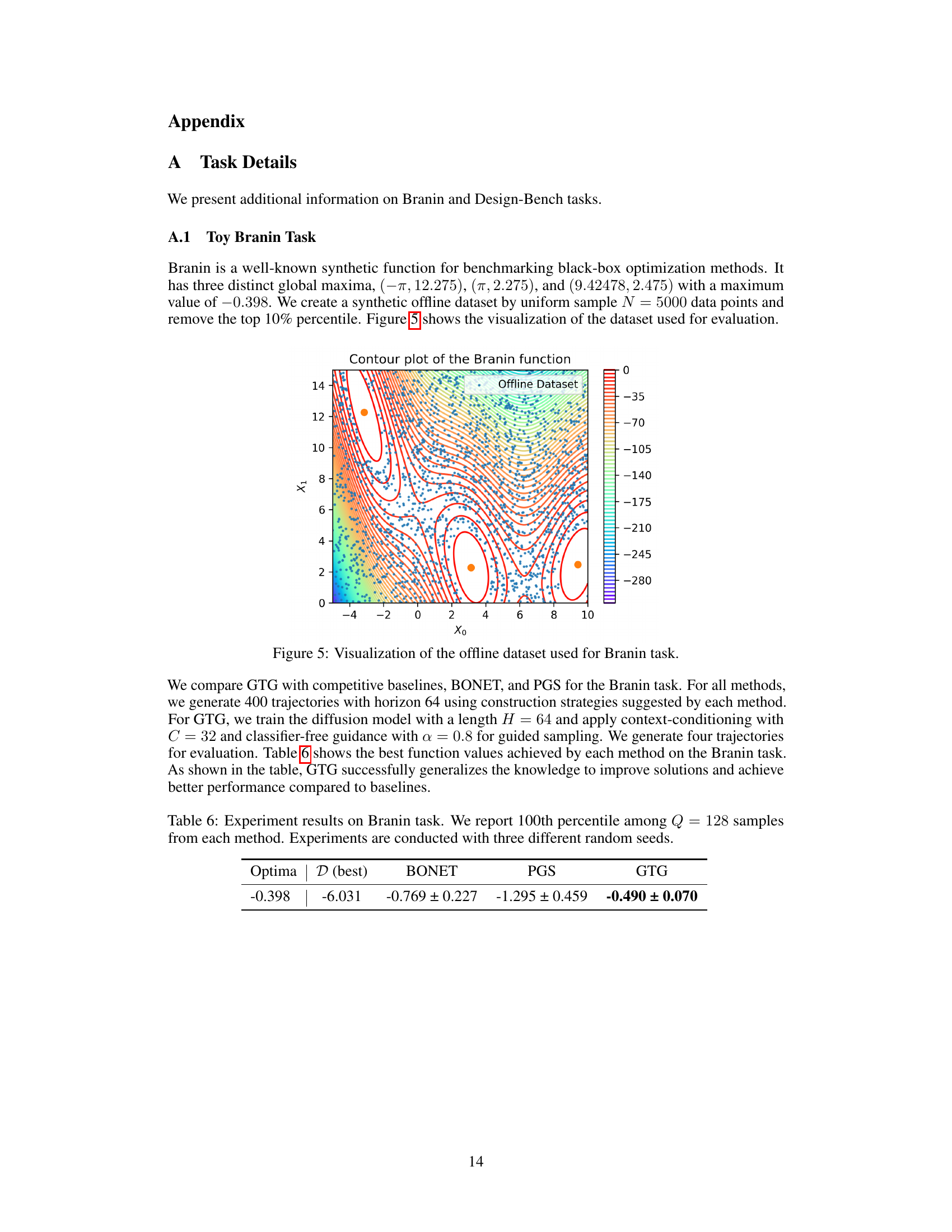
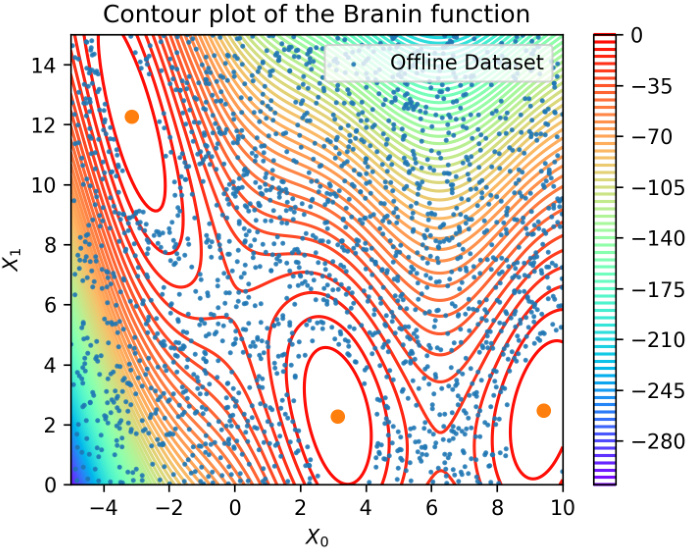
This figure visualizes the trajectories generated by different methods in a 2D toy experiment using the Branin function. It shows that BONET and PGS generate trajectories that are less diverse and less directed towards high-scoring regions compared to GTG. GTG’s trajectories, in contrast, show more exploration and consistent improvement towards high-scoring regions, leveraging the method’s context conditioning and classifier-free guidance.
This figure compares trajectories generated by different methods on the Branin function. (a) shows trajectories from BONET and PGS, which are less diverse and less focused on high-scoring regions. (b) shows the more diverse trajectories generated by the proposed GTG method, demonstrating its ability to explore the search space more effectively. (c) illustrates the guided sampling process used by GTG, where the model generates trajectories conditioned on context data points and high score values, enabling exploration beyond the initial dataset.
This figure compares the trajectories generated by three different methods: BONET, PGS, and the proposed method GTG. It shows that BONET and PGS generate trajectories that are less diverse and don’t effectively explore the design space, while GTG produces more diverse trajectories that move towards higher-scoring regions. The subfigures highlight the differences in trajectory generation and how the inclusion of context data points helps to guide the trajectories.

This figure provides a high-level overview of the proposed GTG (Guided Trajectory Generation) method, illustrating the four main steps involved. Step 1 focuses on constructing synthetic trajectories from an existing dataset, leveraging locality bias for consistent improvement. Step 2 involves training a conditional diffusion model to generate trajectories, along with a proxy model for filtering. Step 3 demonstrates how trajectories are sampled from the trained diffusion model using classifier-free guidance and context conditioning for exploration. Finally, Step 4 explains how the generated trajectories are filtered using the proxy model to select high-fidelity designs for final evaluation.

This figure shows a comparison of trajectory generation methods for offline model-based optimization. (a) shows trajectories generated by existing methods BONET and PGS, illustrating their limitations in generating diverse and consistent trajectories. (b) demonstrates GTG’s ability to produce more diverse and effective trajectories. (c) visualizes the sampling process from the trained diffusion model, showcasing how context data points and guidance influence trajectory generation.

This figure compares the trajectories generated by three different methods: BONET, PGS, and the proposed GTG method. Panel (a) shows the trajectories generated by BONET (blue) and PGS (green), illustrating their limitations in generating diverse and consistent trajectories towards high-scoring regions. Panel (b) displays the diverse trajectories generated by GTG (red), demonstrating its ability to explore the design space more effectively. Finally, panel (c) visualizes the trajectories generated by the trained diffusion model with guided sampling, highlighting the use of context data points (red) to condition the generation process and the resulting diverse and high-scoring trajectories (blue).

This figure compares trajectory generation methods for offline model-based optimization (MBO). (a) shows trajectories from baselines BONET and PGS, highlighting their limitations in generating diverse and directed trajectories. (b) presents the proposed GTG method, demonstrating its ability to generate diverse trajectories towards high-scoring regions. (c) visualizes the guided sampling process of GTG, showcasing how it generates trajectories and incorporates context data points for better generalization.

This figure provides a visual overview of the Guided Trajectory Generation (GTG) method’s four main steps. Step 1 involves constructing trajectories from an offline dataset. Step 2 focuses on training a conditional diffusion model and a proxy function. In Step 3, the model generates new trajectories using classifier-free guidance and context conditioning. Finally, Step 4 selects high-fidelity designs by filtering the generated trajectories using the proxy function.
More on tables
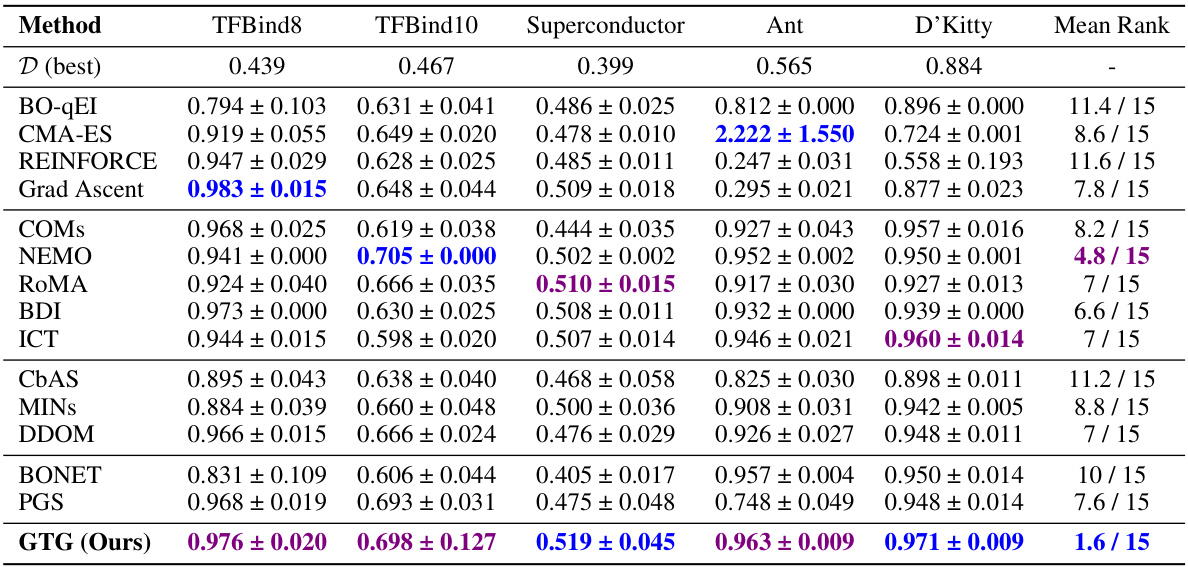
This table presents the results of experiments conducted on various tasks from the Design-Bench benchmark. For each task (TFBind8, TFBind10, Superconductor, Ant, and D’Kitty), the table shows the maximum score achieved by each method among the top 128 candidates, based on the 100th percentile. The best and second-best results for each task are highlighted in blue and violet, respectively. The mean rank across all tasks is provided for comparison.

This table presents the results of experiments conducted on various tasks within the Design-Bench benchmark. The maximum score (100th percentile) achieved among 128 candidates is reported for each method on eight different tasks. The best and second-best results for each task are highlighted in blue and violet, respectively. The table allows comparison of the proposed GTG method against various other offline model-based optimization techniques.

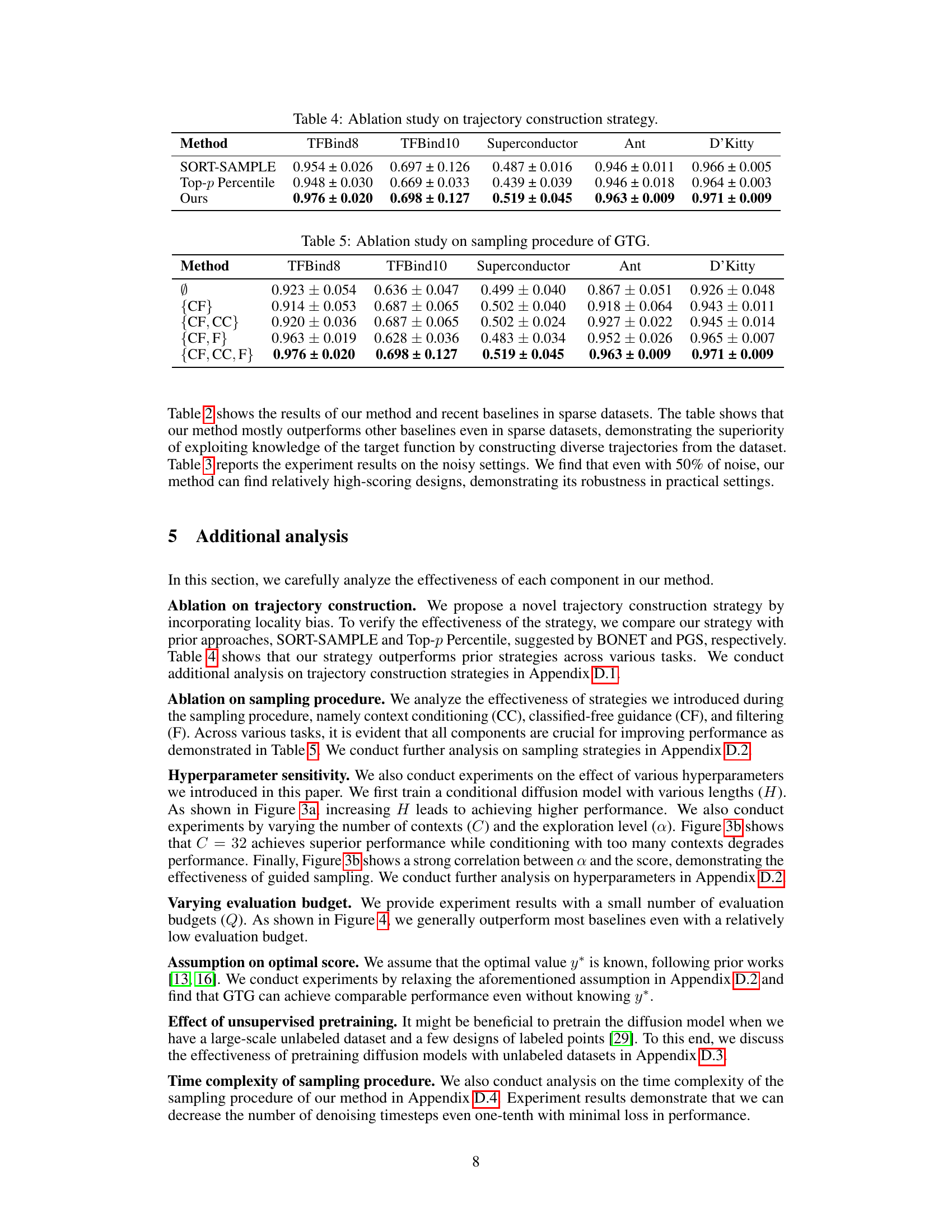
This table presents the ablation study on the trajectory construction strategy used in the GTG method. It compares the performance of three different strategies: SORT-SAMPLE, Top-p Percentile, and the proposed method. The results are shown for five different tasks: TFBind8, TFBind10, Superconductor, Ant, and D’Kitty. Each entry in the table represents the maximum score (100th percentile) achieved among Q=128 candidate designs, along with the standard deviation. The table aims to demonstrate the effectiveness of the proposed trajectory construction method by comparing it to existing baselines.

This table presents the results of an ablation study on the sampling procedure of the Guided Trajectory Generation (GTG) method. It shows the performance of GTG with different combinations of classifier-free guidance (CF), context conditioning (CC), and filtering (F) techniques. The results are presented for five different configurations: without any technique (Ø), only CF, CF and CC, CF and F, and all three techniques (CF, CC, F). The performance is evaluated across five different Design-Bench tasks: TFBind8, TFBind10, Superconductor, Ant, and D’Kitty.

This table presents the results of experiments conducted on various tasks from the Design-Bench benchmark. For each task, the maximum score achieved among the top 128 candidates selected by different methods is shown. The best and second-best results for each task are highlighted in blue and violet, respectively. The methods compared include various offline model-based optimization approaches. The mean rank of each method across all tasks is included to allow for comparison.

This table presents the results of experiments conducted on various tasks from the Design-Bench benchmark. For each task, the maximum score (100th percentile) achieved among 128 candidate designs is reported, along with standard deviation. The best and second-best results are highlighted in blue and violet respectively. The table allows for comparison of the proposed method (GTG) against several baseline methods.
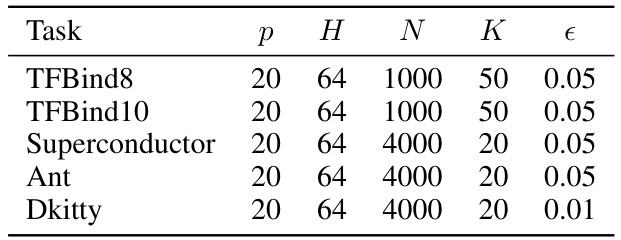
This table presents the results of experiments conducted on various tasks from the Design-Bench benchmark. The maximum score (100th percentile) achieved among 128 candidate designs is reported for each task and method. The best and second-best results for each task are highlighted in blue and violet respectively. The table allows for a comparison of the performance of different optimization methods across multiple tasks of varying complexity.

This table presents the results of experiments conducted on various tasks from the Design-Bench benchmark. The table shows the maximum score achieved (100th percentile) among the top 128 candidates selected by different optimization methods. The best and second-best performing methods for each task are highlighted in blue and violet, respectively. The results provide a comparison of the performance of various offline model-based optimization methods across multiple design tasks.

This table presents the results of experiments conducted on various tasks within the Design-Bench benchmark. The maximum score (100th percentile) achieved among 128 candidate designs is reported for each task. The table compares various optimization methods, highlighting the best-performing method for each task and indicating the second-best performer.
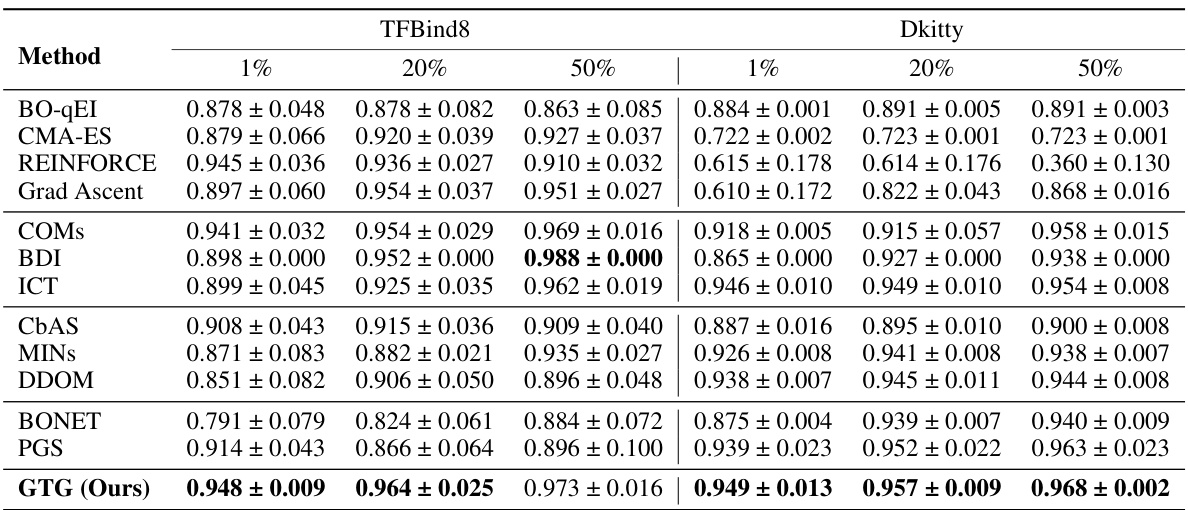
This table presents the results of experiments conducted on various tasks from the Design-Bench benchmark. For each task, the maximum score achieved among the top 128 candidate designs is reported. The table compares the performance of the proposed GTG method to several baseline methods, highlighting the best and second-best performers for each task. The mean rank across all tasks is also included to provide an overall comparison.

This table compares the performance of two different sampling strategies for guiding the diffusion model in GTG: inpainting and classifier-free guidance. The results are presented for five different tasks from the Design-Bench benchmark: TFBind8, TFBind10, Superconductor, Ant, and D’Kitty. The table shows that the classifier-free guidance strategy generally outperforms the inpainting strategy across all five tasks.

This table presents the results of experiments conducted on various tasks from the Design-Bench benchmark. For each task, the maximum score (100th percentile) achieved among 128 candidate designs is reported. The table compares the performance of the proposed GTG method against various baselines, highlighting the best and second-best performing methods for each task.

This table presents the results of experiments conducted on various tasks from the Design-Bench benchmark. The maximum score achieved (100th percentile) among 128 candidate designs is reported for each task and method. The best and second-best performing methods for each task are highlighted in blue and violet respectively. The table allows for a comparison of the proposed GTG method against several baseline optimization approaches.

This table presents the results of experiments comparing the performance of GTG with and without pretraining on a synthetic dataset. The results show that pretraining generally improves the performance, particularly in sparse data settings. Three random seeds were used for each experiment. The table shows the maximum score (100th percentile) for each method across five different Design-Bench tasks.
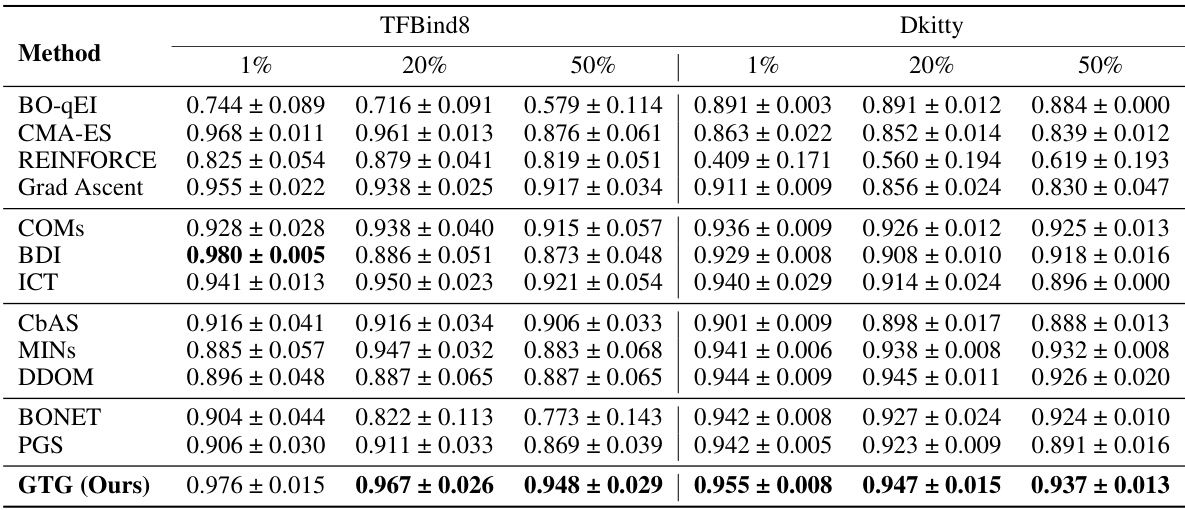
This table presents the results of experiments conducted on various tasks from the Design-Bench benchmark. For each task, the maximum score (100th percentile) achieved among 128 candidate designs generated by different methods is reported. The table allows comparison of different optimization methods (BO-qEI, CMA-ES, REINFORCE, Grad Ascent, COMS, NEMO, ROMA, BDI, ICT, CbAS, MINS, DDOM, BONET, PGS, and GTG (the authors’ method)) across various Design-Bench tasks (TFBind8, TFBind10, Superconductor, Ant, and D’Kitty). The best performing method for each task is highlighted in blue, and the second-best is highlighted in violet.
This table presents the results of experiments conducted on various tasks within the Design-Bench benchmark. The maximum score achieved (100th percentile) among 128 design candidates is reported for each of several different optimization methods on a selection of Design-Bench tasks. The best result for each task is highlighted in blue, and the second-best is highlighted in violet. This provides a comparison of the performance of the proposed GTG method against various baseline methods.
Full paper#