TL;DR#
Concept Bottleneck Models (CBMs) enhance model interpretability by allowing human intervention to correct mispredicted concept values. However, traditional CBMs treat concepts independently, limiting intervention effectiveness. They also require manual concept annotation, a time-consuming process.
This work introduces Stochastic Concept Bottleneck Models (SCBMs), which model concept dependencies using a multivariate normal distribution. This approach enables efficient, scalable computation of intervention effects. SCBMs also use a novel intervention strategy based on confidence regions and demonstrate improved intervention effectiveness on various datasets, even with CLIP-inferred concepts, thereby bypassing the need for manual annotation. The study demonstrates significant improvements in intervention effectiveness, particularly when utilizing a small number of interventions.
Key Takeaways#
Why does it matter?#
This paper is important because it significantly improves the interpretability and usability of Concept Bottleneck Models (CBMs), a crucial area in machine learning. By addressing the limitations of existing CBMs, this research facilitates more effective human-in-the-loop interventions, enhances model transparency, and opens up new avenues for research in various applications where interpretability is paramount.
Visual Insights#
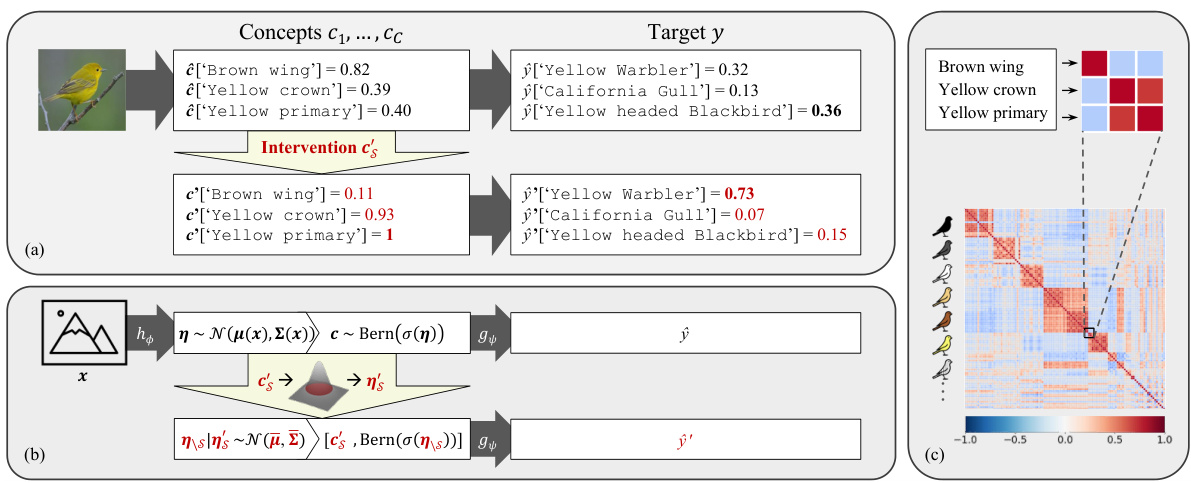
🔼 This figure provides a visual overview of the proposed Stochastic Concept Bottleneck Model (SCBM). Panel (a) shows an example of user intervention on the CUB dataset, highlighting how SCBM adjusts correlated concepts after a single intervention unlike traditional CBMs. Panel (b) illustrates the intervention procedure schematically, emphasizing how user input influences the logits of remaining concepts. Finally, panel (c) displays a visualization of the learned global dependency structure, represented as a correlation matrix for the 112 concepts in the CUB dataset, offering insights into the learned relationships between concepts.
read the caption
Figure 1: Overview of the proposed method for the CUB dataset. (a) A user intervenes on the concept of 'primary color: yellow'. Unlike CBMs, our method then uses this information to adjust the predicted probability of correlated concepts, thereby affecting the target prediction. (b) Schematic overview of the intervention procedure. A user's intervention c's is used to infer the logits ns of the remaining concepts. (c) Visualization of the learned global dependency structure as a correlation matrix for the 112 concepts of CUB (Wah et al., 2011). Characterization of concepts on the left.

🔼 This table presents the concept and target accuracy of different models on three datasets (Synthetic, CUB, and CIFAR-10) before any interventions are made. The results are averaged over ten different random seeds, and the best-performing model for each dataset and metric is highlighted in bold, while the second-best is underlined. The table provides a baseline comparison of the models before any user interaction.
read the caption
Table 1: Test-set concept and target accuracy (%) prior to interventions. Results are reported as averages and standard deviations of model performance across ten seeds. For each dataset and metric, the best-performing method is bolded and the runner-up is underlined.
In-depth insights#
SCBM Framework#
The Stochastic Concept Bottleneck Model (SCBM) framework offers a novel approach to concept bottleneck models (CBMs) by explicitly modeling dependencies between concepts using a multivariate normal distribution. This contrasts with previous CBMs that often assume independence. The framework’s key strength lies in its ability to improve intervention effectiveness. A single intervention on one concept influences correlated concepts, making the process of correcting mispredictions more efficient. This improvement is achieved through a learnable non-diagonal covariance matrix, capturing concept relationships effectively. The explicit parameterization allows for an effective intervention strategy based on the confidence region, further enhancing user interaction and accuracy. Joint training of concept and target predictors is enabled by the distributional parameterization, maintaining the efficiency of traditional CBMs.
Intervention Strategy#
The paper’s proposed intervention strategy for Stochastic Concept Bottleneck Models (SCBMs) is a significant advancement over existing methods. Instead of individually adjusting each mispredicted concept, SCBMs leverage the learned concept dependencies to propagate the effect of a single intervention across correlated concepts, enhancing efficiency. This dependency-aware intervention relies on a multivariate normal distribution parameterization of concept logits, allowing for a computationally efficient and scalable approach. Further refining the strategy, the authors introduce a likelihood-based confidence region to guide interventions, ensuring that adjustments remain plausible and effective. This approach addresses potential issues of the traditional percentile-based intervention method used in CBMs where interventions might be ineffective. By focusing on concepts the model predicts poorly, the intervention becomes more targeted and impactful. This sophisticated approach improves effectiveness, particularly when only a few interventions are performed, thus addressing the practical limitation of time-consuming manual adjustments in standard CBMs.
Empirical Results#
The empirical results section of a research paper is crucial for validating the claims made. A strong section would begin with a clear description of the datasets used, highlighting their characteristics and suitability for the research question. It should then present the evaluation metrics used, justifying their selection and relevance. The results themselves should be presented concisely and clearly, using tables and figures, and focusing on comparing different approaches to the problem. Statistical significance should be explicitly addressed, ideally with appropriate error bars or p-values. Importantly, the results should be interpreted thoughtfully, connecting the findings back to the paper’s hypotheses and discussing any limitations or unexpected results. A good empirical results section is not just about presenting numbers; it’s about using data to tell a compelling story that supports the paper’s claims. Finally, it is vital that the results are presented in a way that’s both easy to understand and readily reproducible by others, bolstering the overall credibility of the research.
Concept Dependence#
The concept of ‘Concept Dependence’ in this research paper centers on how the prediction of one concept influences the prediction of others within a model. The authors challenge traditional approaches that treat concepts independently, arguing that such models overlook valuable relationships between concepts. This dependence, they suggest, is crucial for improving intervention effectiveness; that is, when a user corrects a model’s prediction for one concept, this correction should propagate to related concepts, leading to more accurate overall predictions. The paper introduces a novel method to explicitly model these dependencies, improving intervention efficiency compared to previous, independent methods. A key contribution is the use of a multivariate normal distribution to represent concept logits, allowing for efficient computation of these dependencies during both training and inference. This approach’s strength lies in its ability to enhance the interpretability and usability of the model through a more comprehensive understanding of how concepts relate to each other, improving the overall prediction accuracy after interventions.
Future Work#
The paper’s “Future Work” section hints at several promising research directions. Extending SCBMs beyond binary concepts to handle continuous data is crucial for broader applicability. Addressing the quadratic memory complexity of the covariance matrix is vital for scaling to larger concept sets. Further research should explore how to incorporate user uncertainty into the intervention strategy, acknowledging that human interventions are not always perfectly accurate. The authors also suggest investigating the use of a side channel to complement the covariance structure and potentially reduce information leakage, a known issue with concept bottleneck models. Finally, combining SCBMs with techniques for automatic concept discovery would significantly improve usability and reduce the need for manual annotation.
More visual insights#
More on figures
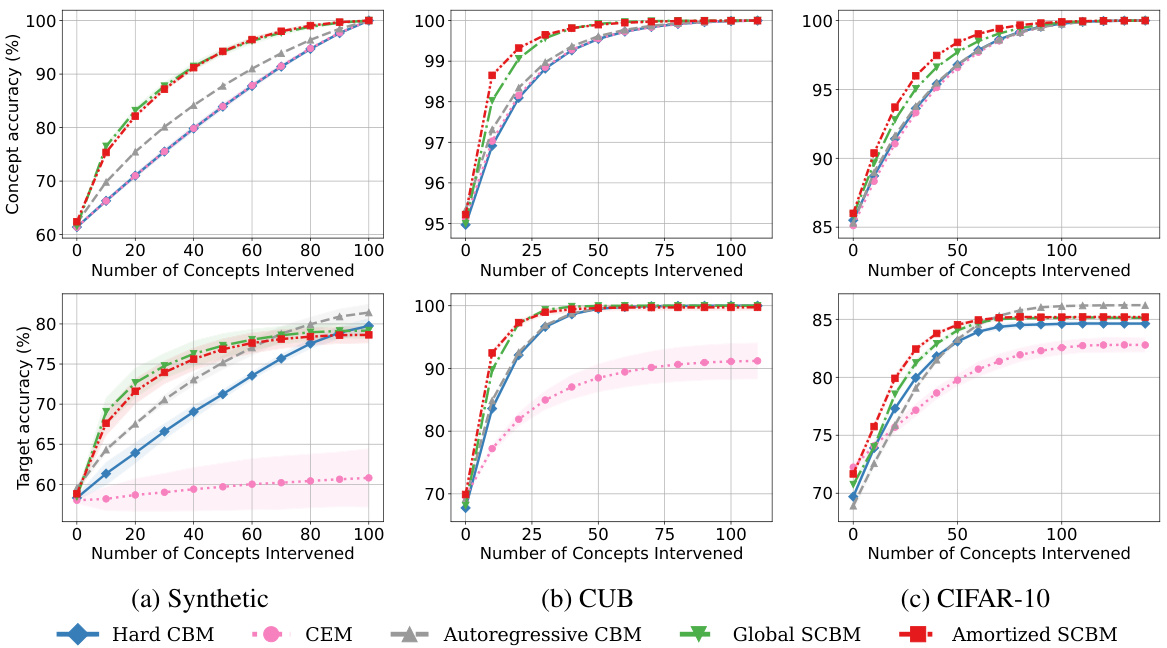
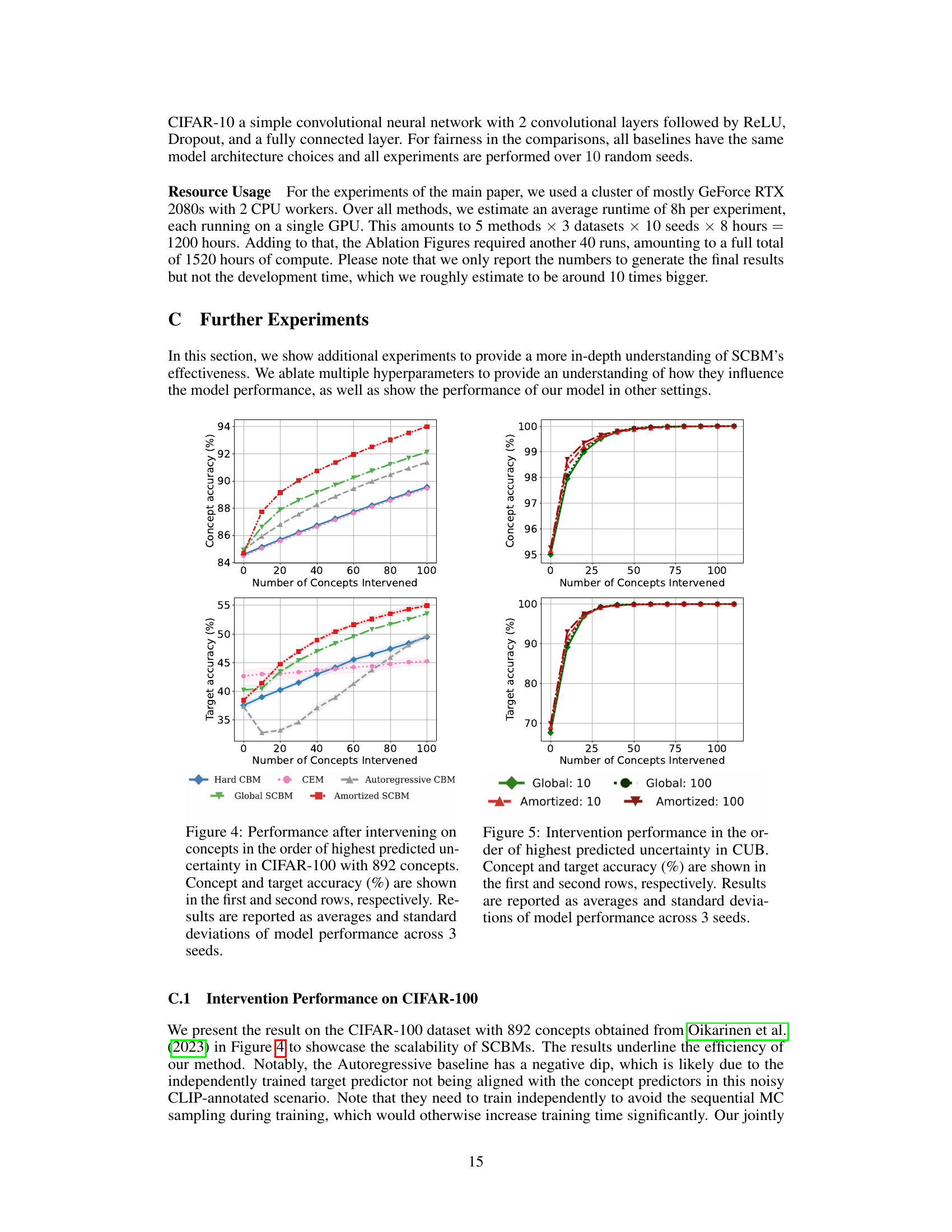
🔼 This figure displays the concept and target accuracy after intervening on concepts, ordered by their predicted uncertainty. The x-axis represents the number of concepts intervened on, while the y-axis shows the accuracy. Separate lines represent different models (Hard CBM, CEM, Autoregressive CBM, Global SCBM, Amortized SCBM). The figure visually compares the effectiveness of different models in improving accuracy through interventions, highlighting the performance of the proposed SCBM models.
read the caption
Figure 2: Performance after intervening on concepts in the order of highest predicted uncertainty. Concept and target accuracy (%) are shown in the first and second rows, respectively. Results are reported as averages and standard deviations of model performance across ten seeds.

🔼 This figure displays the results of intervening on concepts based on their predicted uncertainty. It shows how concept and target accuracy improve as more concepts are corrected. The graphs compare the performance of several models (Hard CBM, CEM, Autoregressive CBM, Global SCBM, Amortized SCBM) across three datasets (Synthetic, CUB, CIFAR-10). The x-axis represents the number of concepts intervened on, while the y-axis represents concept and target accuracy, respectively. The results highlight the superior performance of SCBMs, particularly in scenarios with a limited number of interventions.
read the caption
Figure 2: Performance after intervening on concepts in the order of highest predicted uncertainty. Concept and target accuracy (%) are shown in the first and second rows, respectively. Results are reported as averages and standard deviations of model performance across ten seeds.
🔼 This figure presents the results of experiments on the effects of interventions on model performance. Three datasets (Synthetic, CUB, and CIFAR-10) are shown across two metrics: concept accuracy and target accuracy. The x-axis represents the number of concepts intervened on, and the y-axis represents the accuracy. For each dataset, multiple lines show the performance of different models (Hard CBM, CEM, Autoregressive CBM, Global SCBM, and Amortized SCBM). The curves illustrate how the accuracy changes as more concepts are corrected, demonstrating the effectiveness of the proposed SCBM method in improving accuracy with interventions.
read the caption
Figure 2: Performance after intervening on concepts in the order of highest predicted uncertainty. Concept and target accuracy (%) are shown in the first and second rows, respectively. Results are reported as averages and standard deviations of model performance across ten seeds.

🔼 This figure shows the concept and target accuracy after intervening on concepts in the order of highest predicted uncertainty. The x-axis represents the number of concepts intervened on, while the y-axis shows the accuracy. Separate lines are plotted for each of the methods (Hard CBM, CEM, Autoregressive CBM, Global SCBM, Amortized SCBM) and the results are shown for three datasets: Synthetic, CUB, and CIFAR-10. Error bars representing standard deviations are included. The results demonstrate the impact of intervening on concepts on the overall accuracy of both concept prediction and target prediction, highlighting the superior performance of SCBMs, especially when only a small number of interventions are performed. The different datasets allow for the comparison of model performance under various conditions and highlight the adaptability of the proposed SCBM approach.
read the caption
Figure 2: Performance after intervening on concepts in the order of highest predicted uncertainty. Concept and target accuracy (%) are shown in the first and second rows, respectively. Results are reported as averages and standard deviations of model performance across ten seeds.
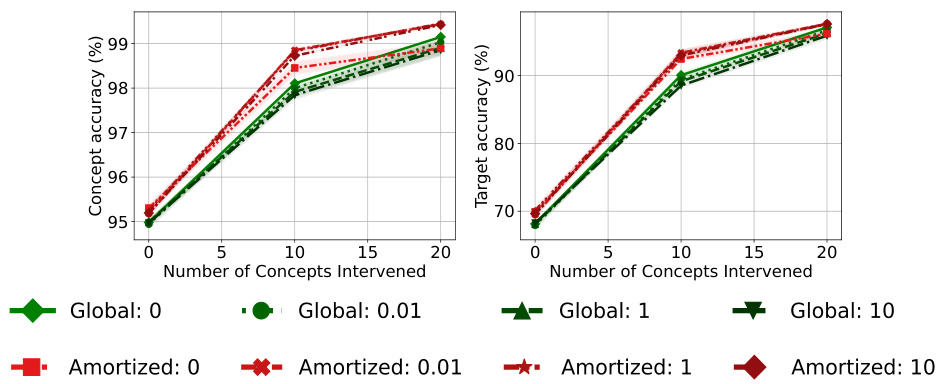
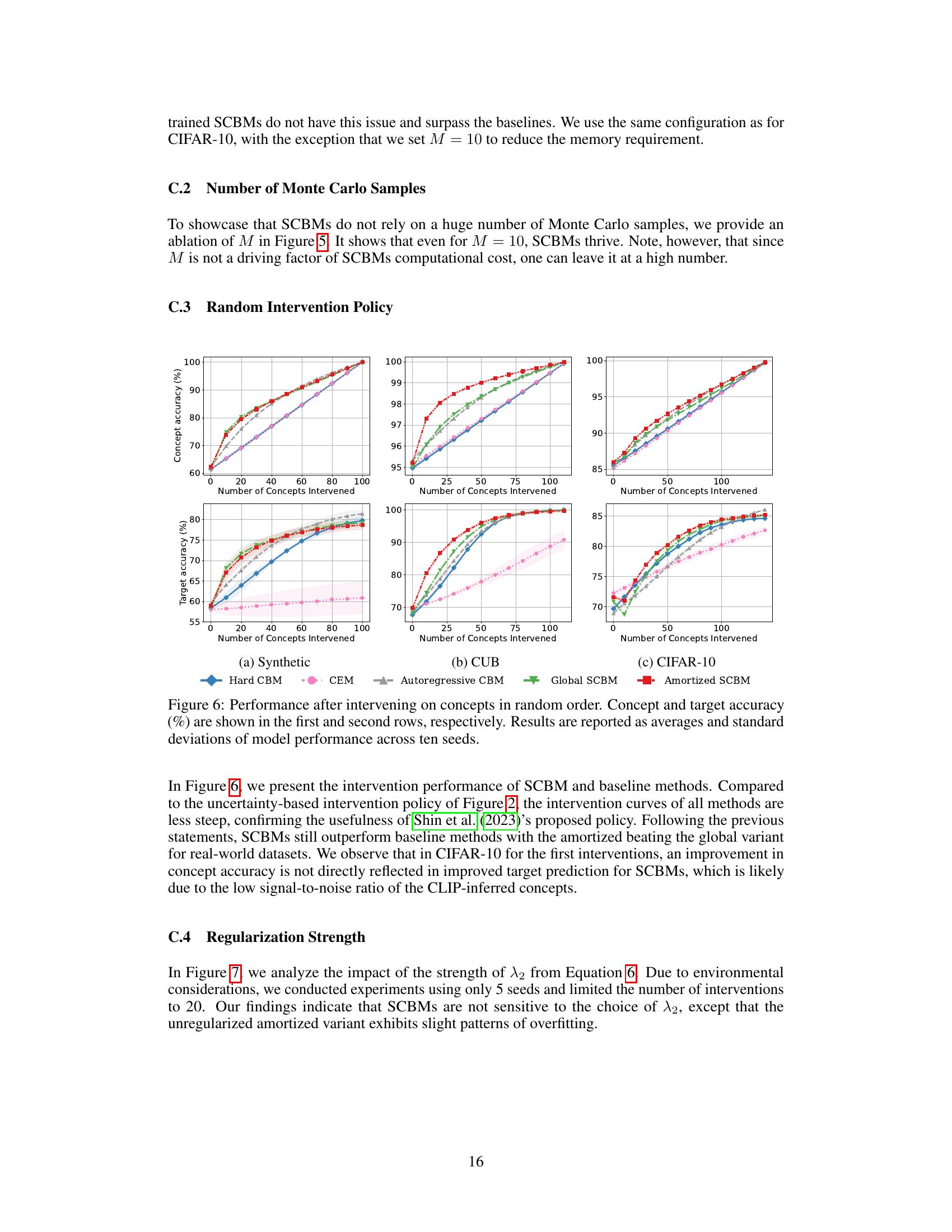
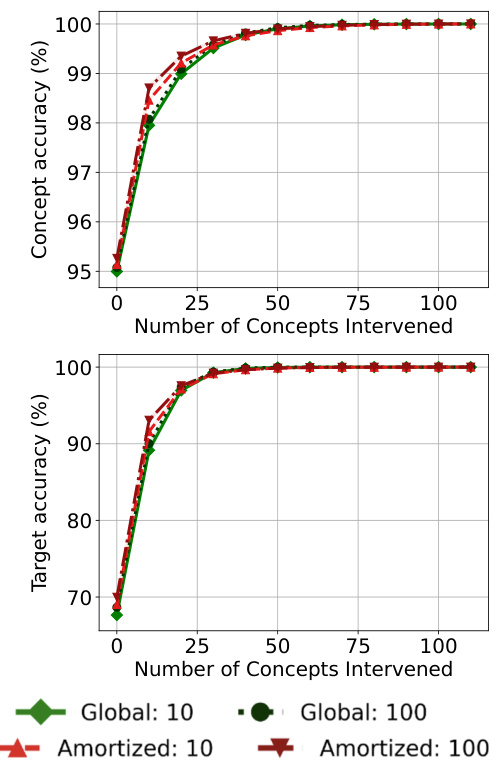
🔼 This figure displays the results of an experiment on the CUB dataset to analyze how different regularization strengths (λ2) affect the performance of the Stochastic Concept Bottleneck Models (SCBMs). The x-axis represents the number of concepts intervened upon, while the y-axis shows the concept accuracy and target accuracy. Separate lines are plotted for both the global and amortized SCBM variants, each with several different λ2 values (0, 0.01, 1, 10). The results show that the performance (both concept and target accuracy) changes depending on the regularization strength and the variant of the model.
read the caption
Figure 7: Performance on CUB after intervening on concepts in the order of highest predicted uncertainty with differing regularization strengths. Concept and target accuracy (%) are shown in the first and second columns, respectively. Results are reported as averages and standard deviations of model performance across five seeds. For each SCBM variant, we choose a darker color, the higher the regularization strength of λ2.
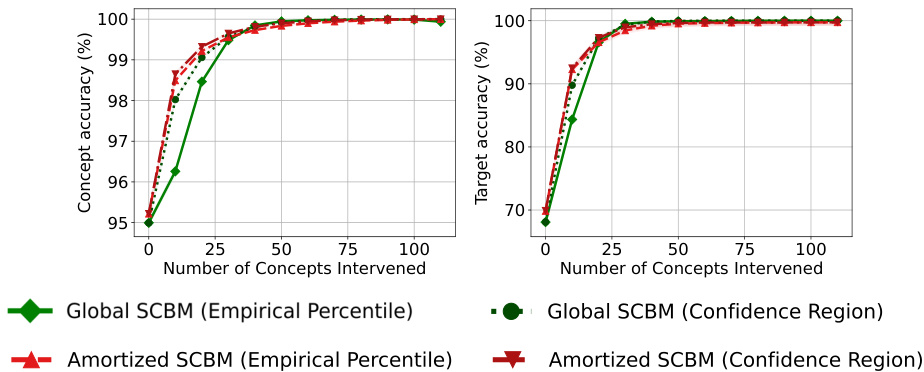
🔼 This figure compares the performance of different models (Hard CBM, CEM, Autoregressive CBM, Global SCBM, and Amortized SCBM) after intervening on a increasing number of concepts, ordered by their predicted uncertainty. The x-axis represents the number of concepts intervened on, while the y-axis shows the concept accuracy and target accuracy. The plots show that SCBMs significantly outperform other methods, especially when only a small number of interventions are performed. This highlights the effectiveness of SCBMs in modeling concept dependencies and improving target prediction.
read the caption
Figure 2: Performance after intervening on concepts in the order of highest predicted uncertainty. Concept and target accuracy (%) are shown in the first and second rows, respectively. Results are reported as averages and standard deviations of model performance across ten seeds.
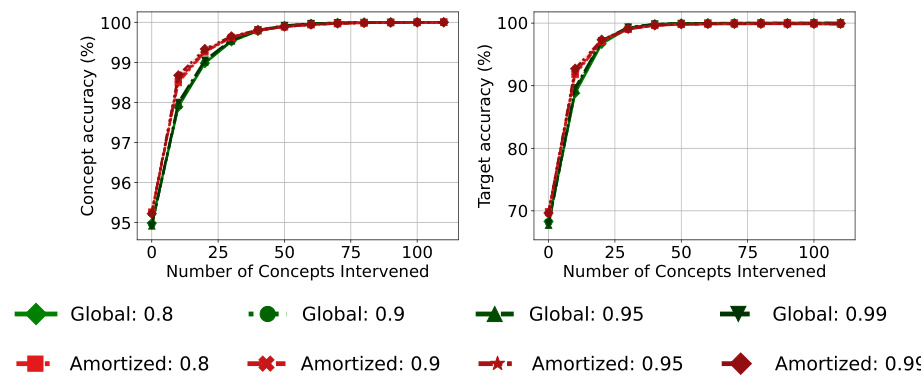
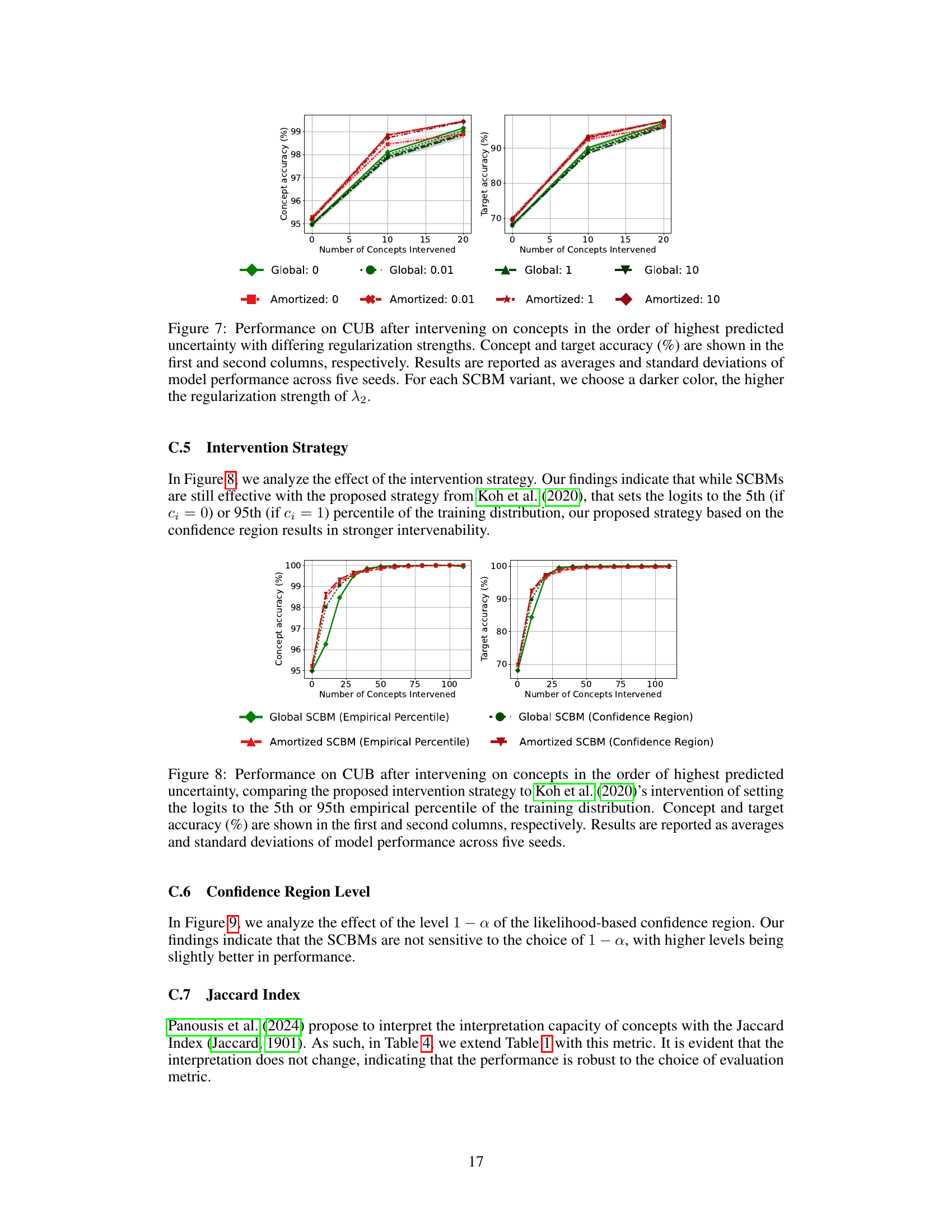
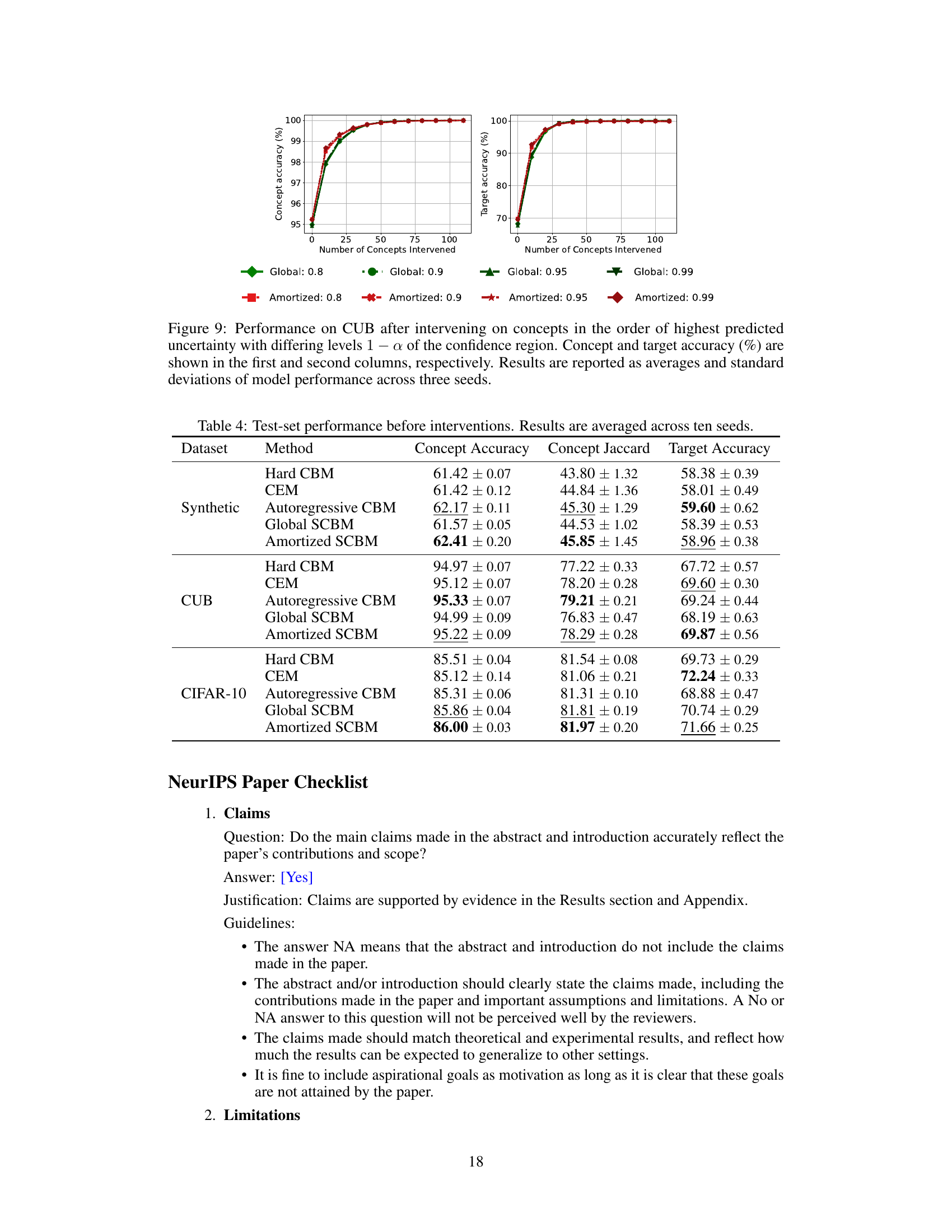
🔼 This figure displays the results of an experiment on the CUB dataset, where the model intervenes on concepts in order of their predicted uncertainty. The different lines represent different confidence region levels (1-α), ranging from 0.8 to 0.99. Both global and amortized covariance matrix versions of the model are tested, and the results show how both concept and target accuracy vary as more concepts are intervened upon. The plot helps to analyze the impact of confidence region level on the intervention effectiveness.
read the caption
Figure 9: Performance on CUB after intervening on concepts in the order of highest predicted uncertainty with differing levels 1−α of the confidence region. Concept and target accuracy (%) are shown in the first and second columns, respectively. Results are reported as averages and standard deviations of model performance across three seeds.
More on tables
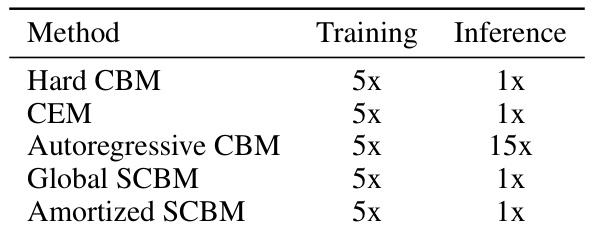
🔼 This table presents the relative training and inference times for different models on the CUB dataset. The training time is relative to the Hard CBM model, which is set as a baseline of 5x. The inference time is also relative to the Hard CBM model, set to 1x. The table helps to understand and compare the computational efficiency of different methods, especially highlighting the significant increase in inference time for the Autoregressive CBM.
read the caption
Table 2: Relative time it takes for one epoch in the CUB dataset when training on the training set, or evaluating on the test set, respectively.
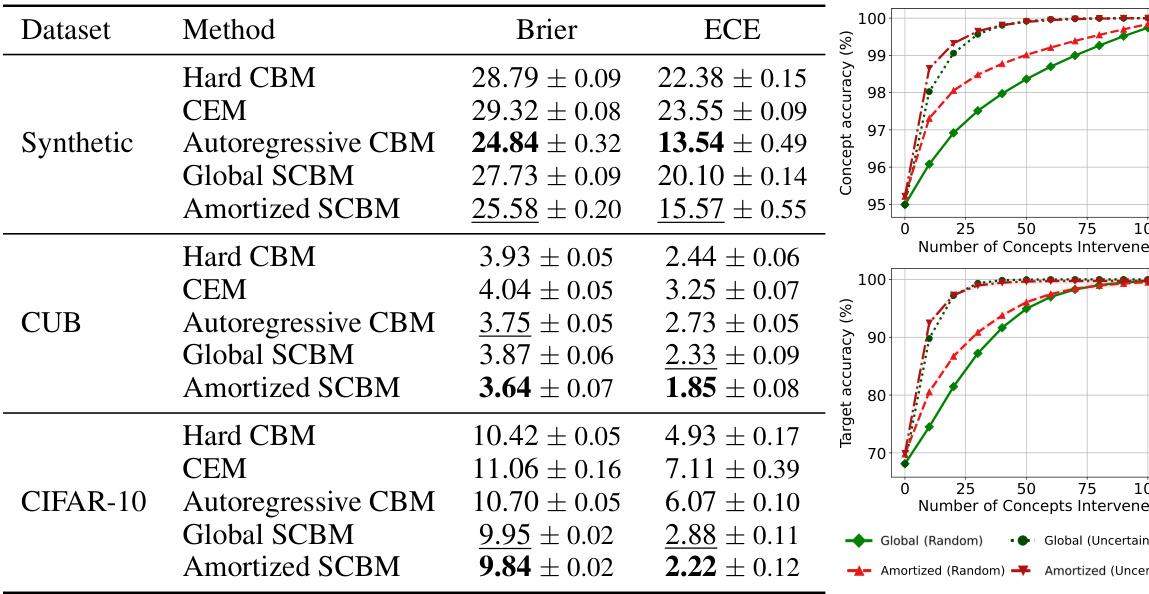
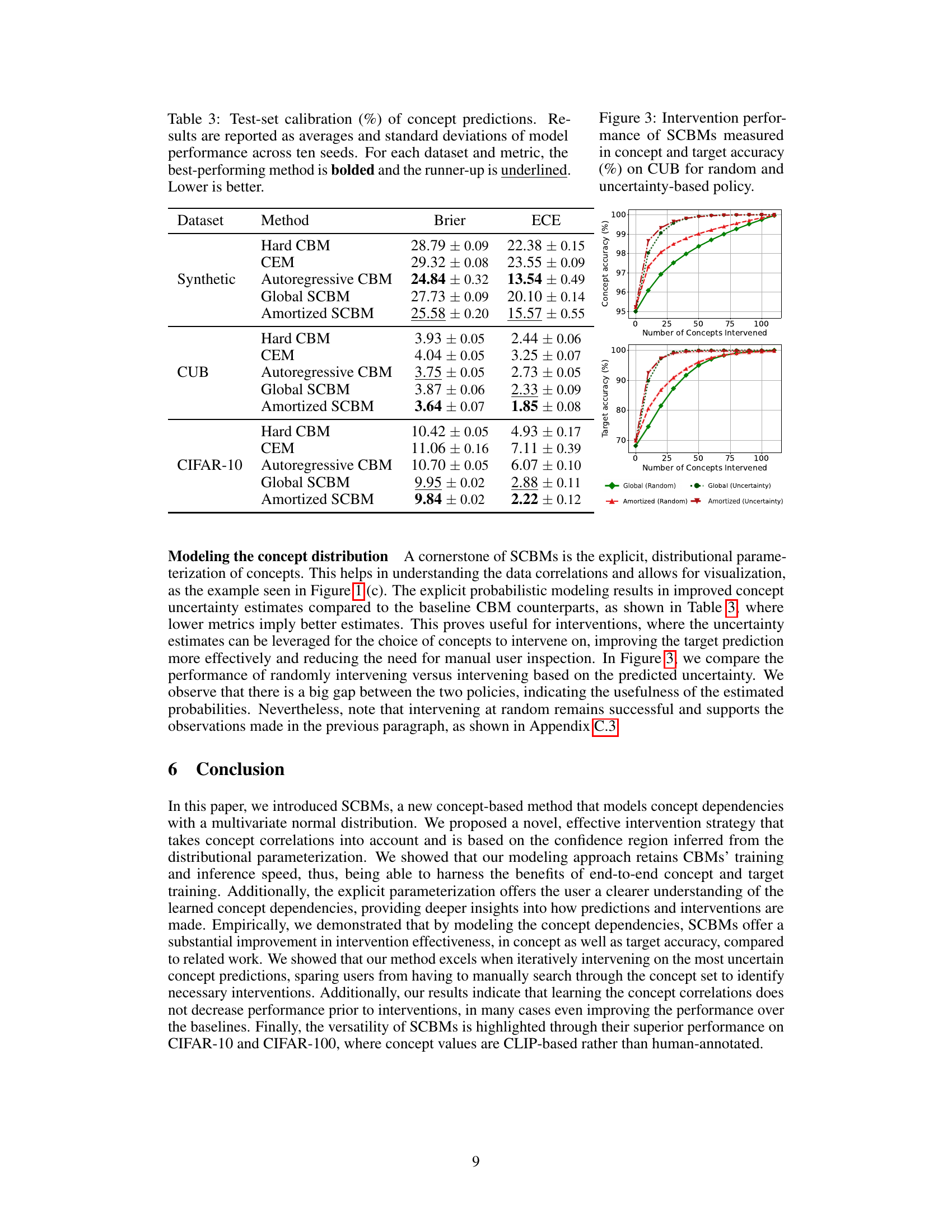
🔼 This table presents the calibration performance of different methods on three datasets (Synthetic, CUB, and CIFAR-10). Calibration is evaluated using two metrics: Brier score and Expected Calibration Error (ECE). Lower values indicate better calibration. The table shows that the proposed Amortized SCBM method generally achieves better calibration than the other methods across all three datasets, demonstrating its improved ability to accurately estimate the uncertainty of its concept predictions.
read the caption
Table 3: Test-set calibration (%) of concept predictions. Results are reported as averages and standard deviations of model performance across ten seeds. For each dataset and metric, the best-performing method is bolded and the runner-up is underlined. Lower is better.

🔼 This table presents the concept and target accuracy of different models before any interventions are performed. The results are averaged over ten different random seeds to provide a reliable measure of performance. The best-performing model for each dataset and metric is highlighted in bold, with the second-best underlined, allowing for easy comparison of model performance across different datasets and metrics.
read the caption
Table 1: Test-set concept and target accuracy (%) prior to interventions. Results are reported as averages and standard deviations of model performance across ten seeds. For each dataset and metric, the best-performing method is bolded and the runner-up is underlined.
Full paper#