↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Cancer radiotherapy treatment involves solving large-scale optimization problems constrained by time and accuracy. Current sparsification methods, while computationally efficient, may lead to suboptimal treatment quality by neglecting crucial small elements in the dose influence matrix. This results in potential side effects or ineffective tumor targeting.
This paper introduces a novel randomized matrix sketching method to address this issue. The method efficiently sparsifies the matrix without significantly impacting the quality of treatment. Experimental results on lung and prostate cancer datasets demonstrate that the proposed algorithm outperforms existing methods, offering significantly improved computational efficiency while maintaining accuracy. This contribution advances both cancer treatment and scientific computing, with potential for broad impact on healthcare.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in cancer radiotherapy, scientific computing, and machine learning. It bridges the gap between these fields by demonstrating the applicability of advanced matrix sketching techniques to tackle computationally intensive optimization problems, paving the way for faster, more efficient, and potentially higher-quality cancer treatment planning. The novel algorithm introduced offers theoretical guarantees and superior empirical performance, opening new avenues for research in efficient large-scale optimization and its applications in healthcare.
Visual Insights#
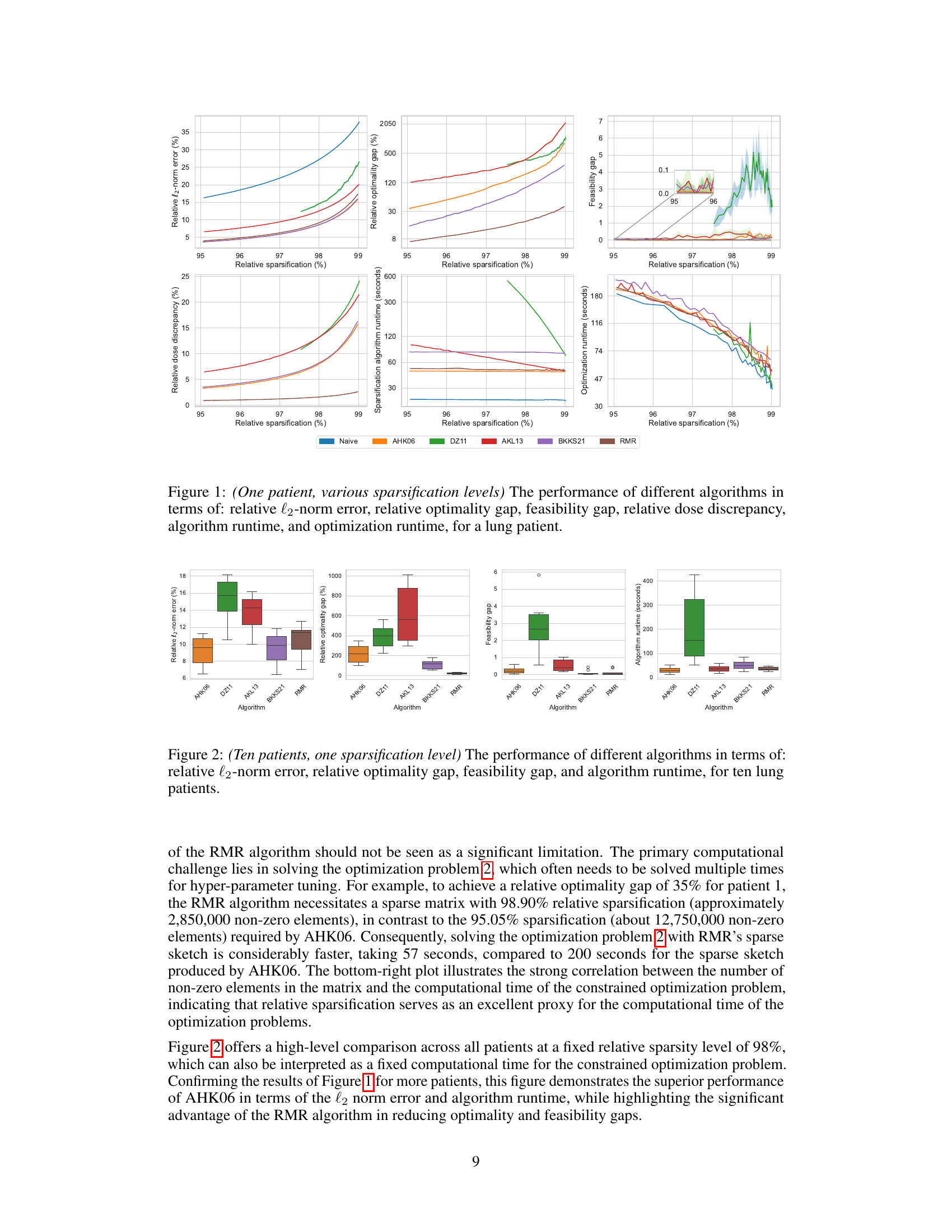
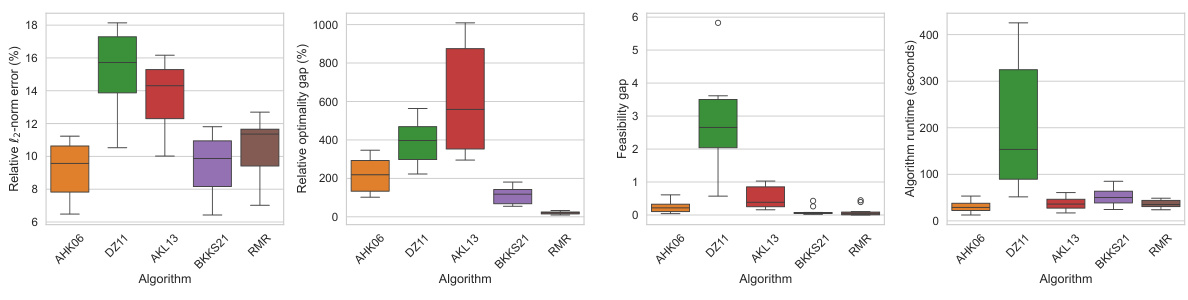
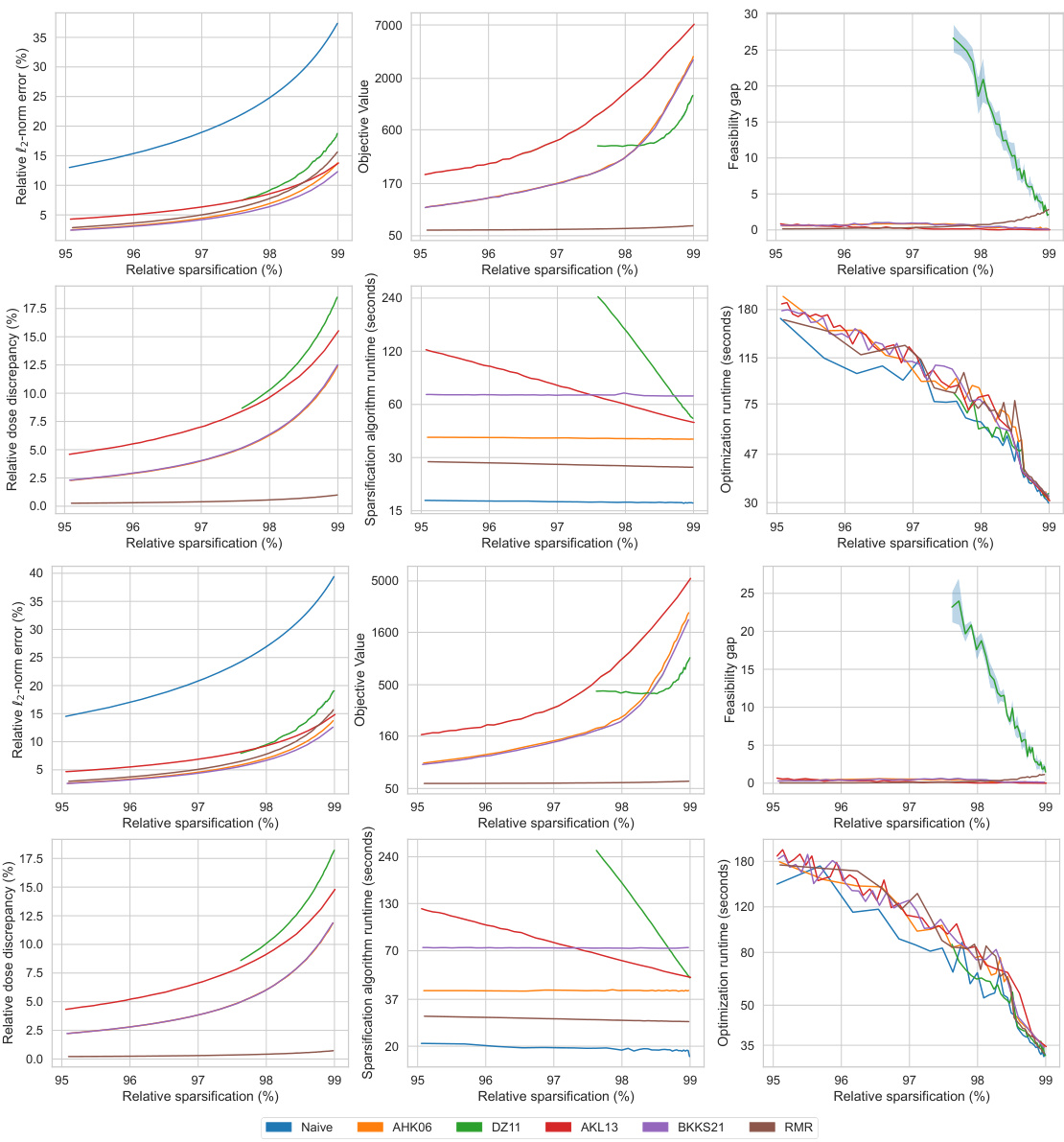
This figure displays the performance comparison of six different matrix sparsification algorithms across various sparsity levels (95% to 99%). The algorithms are evaluated based on several metrics: relative l2-norm error (measuring the accuracy of the approximation), relative optimality gap (the difference in the optimal objective value obtained using the original dense matrix and the sparse approximation), feasibility gap (how much the constraints are violated), relative dose discrepancy (the difference in dose between the original dense and the sparse matrix), algorithm runtime (time required to create the sparse matrix), and optimization runtime (time to solve the optimization problem using the sparse matrix). The results are visualized in multiple subplots, providing a comprehensive view of how each algorithm performs concerning accuracy, efficiency, and the quality of treatment.

This table compares several matrix sparsification algorithms based on their theoretical guarantees. Specifically, it presents the number of non-zero elements in the resulting sparse matrix (related to computational complexity) and the failure probability (chance the approximation isn’t within a specified error bound). Each row represents a different algorithm, with its theoretical bounds expressed using Big O notation, and details on the failure probability. The algorithms are compared to highlight differences in computational efficiency and accuracy.
In-depth insights#
Sparse Matrix Sketch#
Sparse matrix sketching is a crucial technique for dimensionality reduction in large-scale optimization problems. It involves approximating a large, dense matrix with a smaller, sparser one, which significantly reduces computational costs while preserving essential information. The choice of sketching method is critical, as different techniques offer varying trade-offs between accuracy, sparsity, and computational efficiency. Randomized algorithms, such as those based on the Johnson-Lindenstrauss Lemma, have been successful in providing theoretical guarantees on the quality of the approximation. However, the practical performance of these methods depends on the specific characteristics of the matrix and the desired level of sparsity. Optimizing the sparsification process itself is an active area of research, with novel algorithms constantly being developed to improve both theoretical guarantees and practical outcomes. A key challenge is balancing the need for accuracy in the approximation with the need for computational efficiency. The application of sparse matrix sketching to large-scale constrained optimization problems, such as those encountered in healthcare, is an area of growing interest because of the potential to tackle computationally challenging applications. Furthermore, the development of novel and more effective sparsification algorithms remains a topic of significant ongoing research.
RMR Algorithm#
The Randomized Minor-value Rectification (RMR) algorithm, introduced in the context of large-scale constrained optimization problems in cancer radiotherapy, presents a novel approach to matrix sparsification. RMR cleverly balances the speed of deterministic methods with the accuracy of randomized techniques. It begins by deterministically retaining the largest entries of the matrix, a strategy that aligns well with the characteristics of dose influence matrices in radiotherapy. Subsequently, it employs a randomized l1 sampling approach only for the remaining smaller entries, ensuring an unbiased estimator. This hybrid method is highly efficient in practice, exhibiting significant improvements over existing sparsification techniques, particularly at higher sparsity levels. Moreover, RMR offers theoretical guarantees on its performance, ensuring that the sparsified matrix introduces minimal errors in the optimization problem, thus maintaining the quality of radiotherapy treatment. The algorithm’s effectiveness is demonstrated through extensive computational experiments on real-world datasets, highlighting the significant potential of RMR in reducing computational costs while preserving treatment accuracy.
Radiotherapy RT#
Radiotherapy (RT) is a cornerstone of cancer treatment, impacting over half of all cancer patients. Its core challenge lies in precisely targeting cancerous cells while minimizing damage to healthy tissues. This necessitates solving complex, large-scale optimization problems to determine optimal radiation beam shapes and intensities for each patient’s unique anatomy. The process is time-sensitive due to clinical constraints and the need for swift treatment decisions. A significant hurdle is the large, dense matrix involved, often simplified via sparsification to enhance computational efficiency. However, this crude approach can compromise treatment quality. The research paper explores the use of randomized sparse matrix compression techniques, demonstrating significant improvements in computational speed without sacrificing treatment efficacy. This approach leverages advancements in scientific computing to address critical healthcare challenges, potentially transforming cancer care through faster and more accurate treatment planning.
Clinical Impact#
A research paper focusing on improving cancer radiotherapy through advanced matrix sparsification techniques would need a strong ‘Clinical Impact’ section. It should highlight that the proposed method leads to faster treatment planning without compromising treatment quality. This is crucial because faster planning minimizes patient discomfort and potential anatomical changes during treatment. Faster planning is particularly important for modern online adaptive radiotherapy, where speed is paramount. The section must quantify these benefits, perhaps using metrics like reduced processing time or improved dose conformity. It should also address the broader potential, arguing that the computational efficiency could expand access to advanced treatment techniques for more patients. The clinical impact section must also acknowledge any limitations, such as the need for further clinical validation or potential challenges in adapting the method for all cancer types and treatment modalities. Successfully demonstrating a tangible improvement in patient outcomes, such as reduced side effects or improved tumor control rates, is essential to highlight the clinical significance of this work.
Future Directions#
Future research could explore advanced matrix sparsification techniques beyond randomized sketching, potentially improving accuracy and efficiency. Investigating alternative sparsification methods tailored to the specific structure of the dose influence matrix is warranted. Furthermore, robustness analysis against noise and uncertainty in the input data is critical. A key area for exploration is the integration of advanced optimization algorithms which are better suited for sparse systems. Clinical validation is paramount. The promising results obtained in the paper should be thoroughly tested in real-world clinical settings to assess efficacy and safety. Finally, extending the approach to other treatment modalities beyond IMRT and adaptive radiotherapy, where rapid solution times are crucial, would significantly enhance its impact on cancer care. This will require developing methods to handle the dynamics inherent in these advanced treatment techniques.
More visual insights#
More on figures
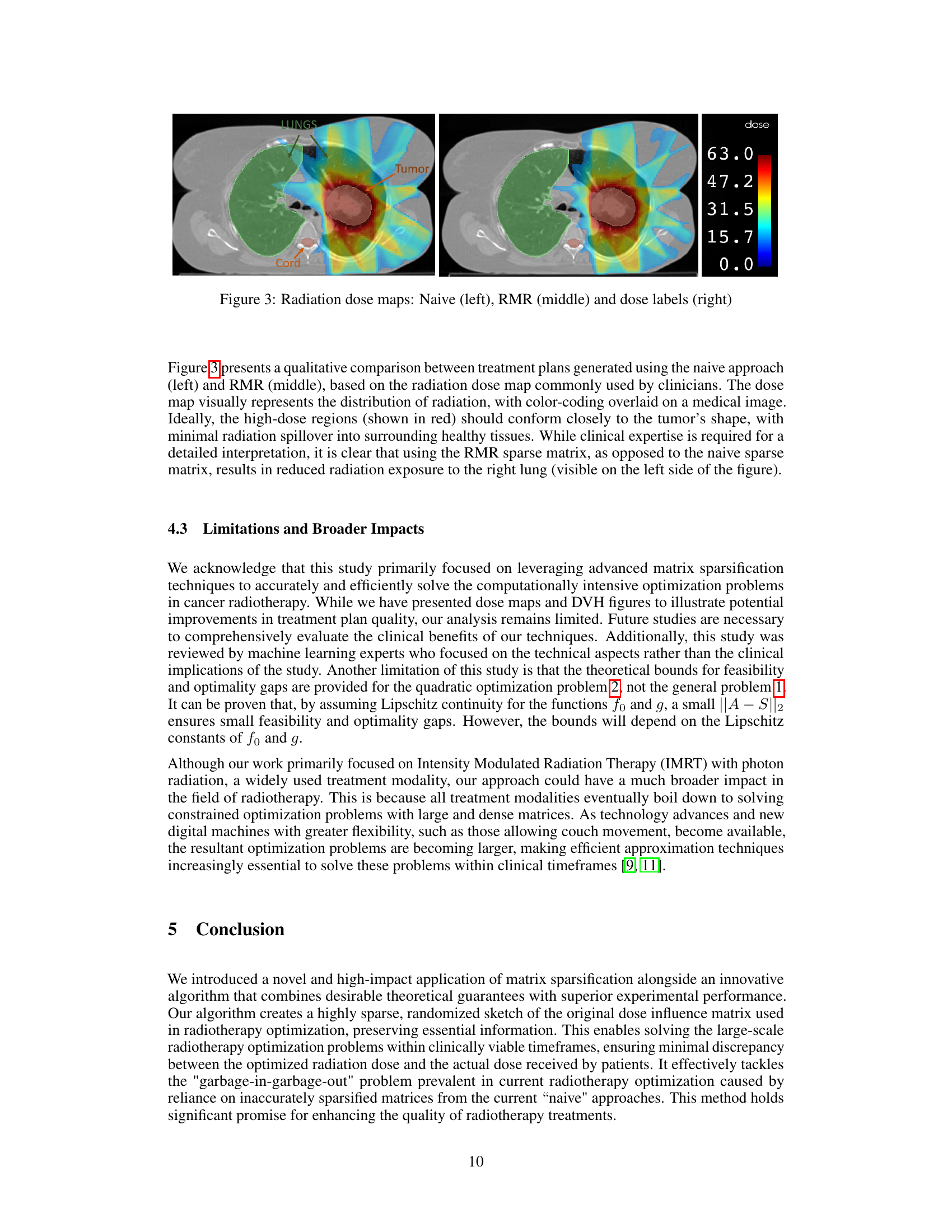
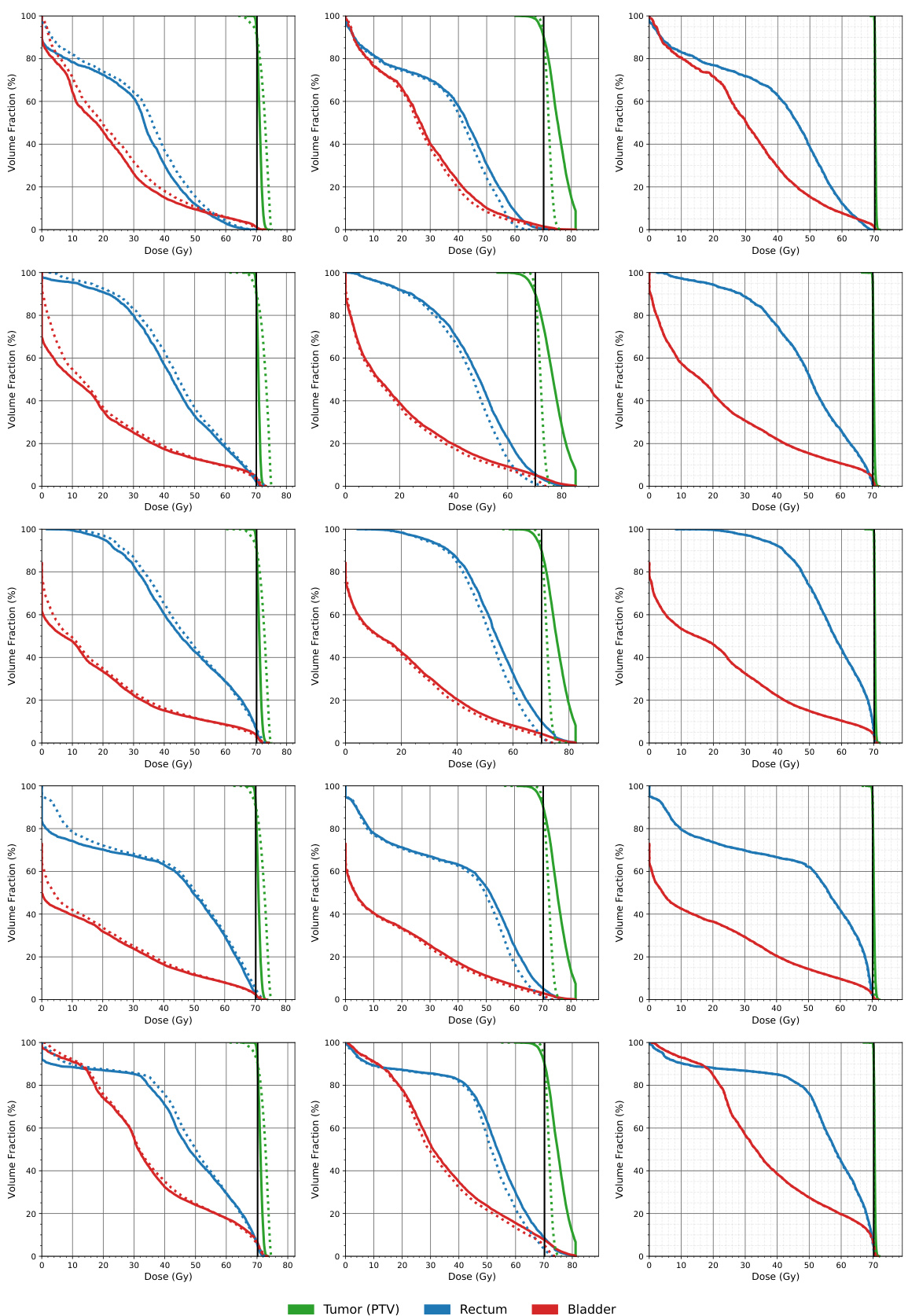
This figure compares the performance of different matrix sparsification algorithms (AHK06, DZ11, AKL13, BKKS21, and RMR) across ten different lung cancer patients. For each algorithm, it shows the relative l2-norm error (how well the sparse matrix approximates the original), relative optimality gap (how close the solution obtained using the sparse matrix is to the optimal solution), feasibility gap (how much the constraints are violated using the sparse matrix), and the algorithm runtime (how long it took to create the sparse matrix). The results are displayed as box plots, which show the median, quartiles, and outliers for each metric. The goal is to demonstrate that the RMR algorithm outperforms other algorithms in terms of accuracy (low optimality and feasibility gaps) while maintaining a reasonable runtime.
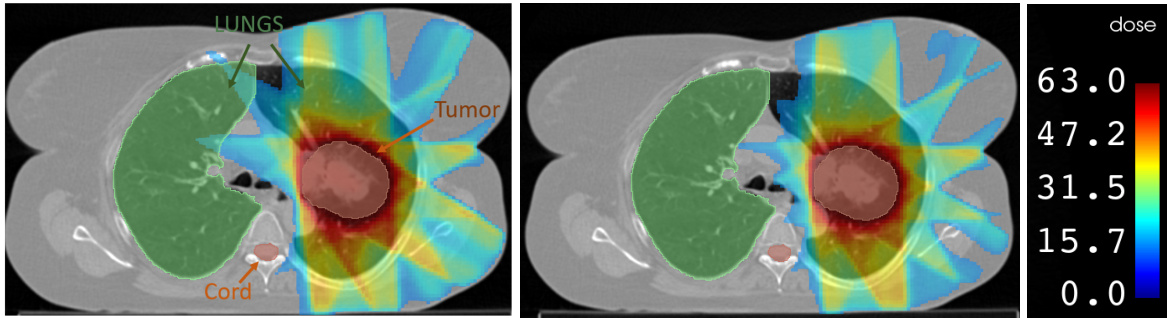
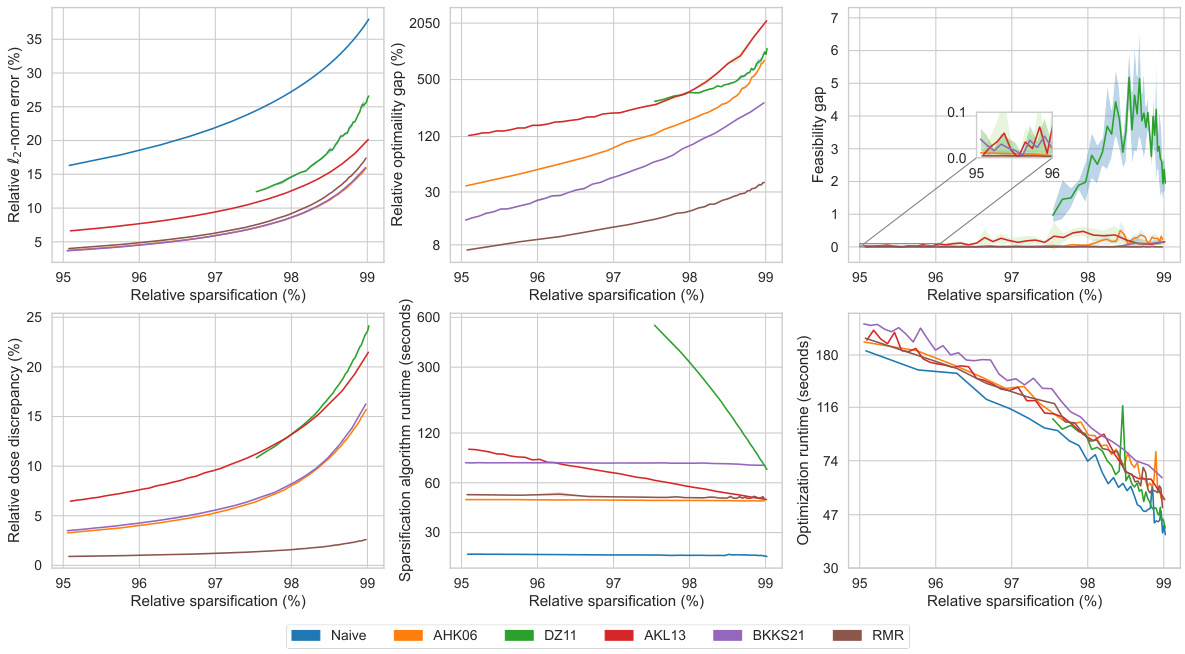
This figure presents a qualitative comparison of radiation dose maps generated using three different approaches: the naive approach (left), the RMR method (middle), and a labeled dose map (right). The dose maps visually represent the distribution of radiation, with color-coding overlaid on a medical image. The goal is to have high-dose regions (red) conform closely to the tumor’s shape, while minimizing radiation spillover to healthy tissues. The comparison shows that using the RMR sparse matrix, as opposed to the naive sparse matrix, results in reduced radiation exposure to the right lung.
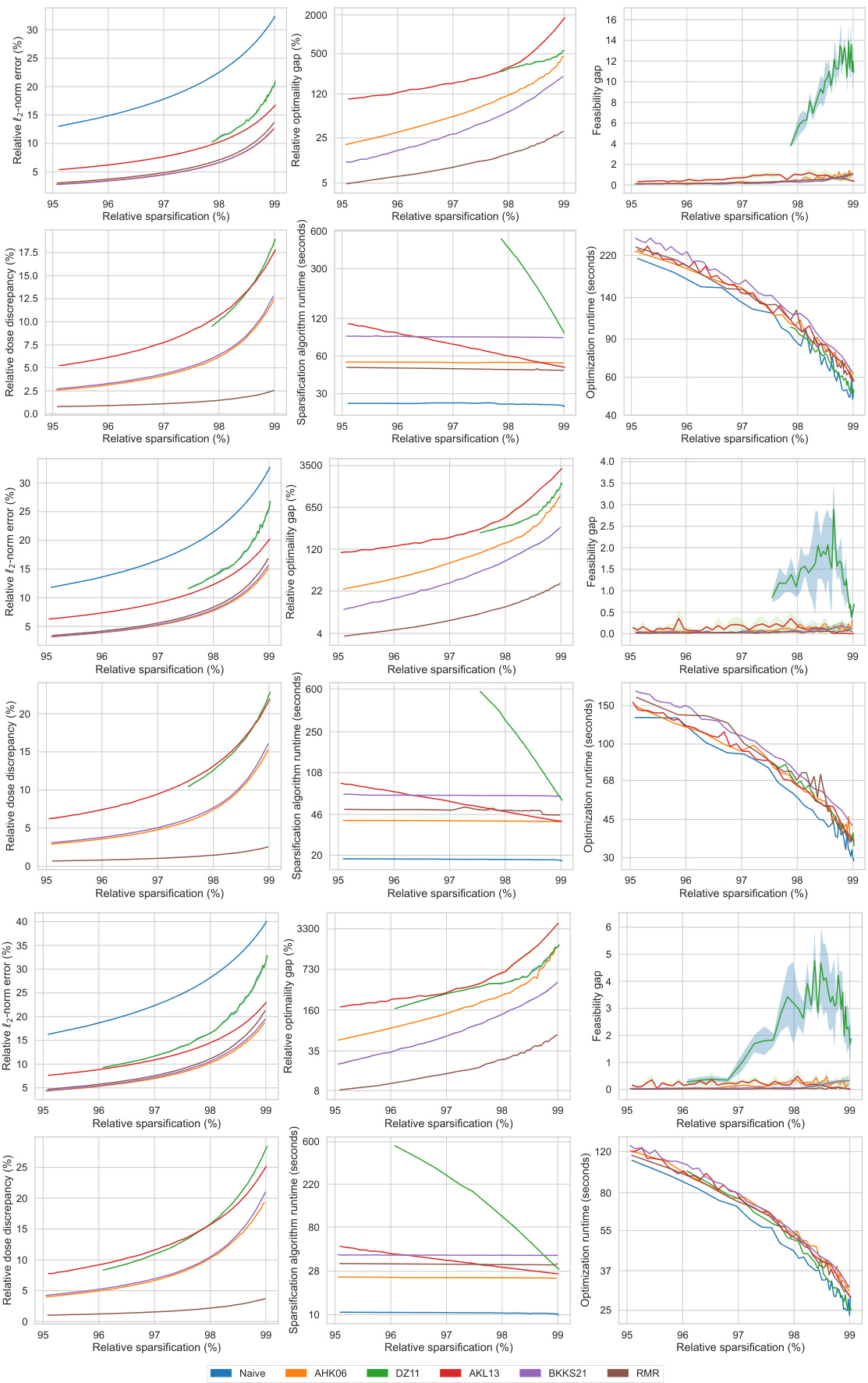
This figure compares the performance of different matrix sparsification algorithms (Naive, AHK06, DZ11, AKL13, BKKS21, and RMR) across various sparsity levels. It shows how each algorithm impacts several key metrics: relative l2-norm error (accuracy of the approximation), relative optimality gap (how close the solution of the sparse approximation is to the optimal solution), feasibility gap (degree to which constraints are violated), relative dose discrepancy (difference between actual and approximated doses), algorithm runtime (time to sparsify the matrix), and optimization runtime (time to solve the optimization problem using the sparse matrix). The results indicate the trade-offs between computational efficiency and solution quality for each method. The RMR method is highlighted for its superior performance in several aspects.
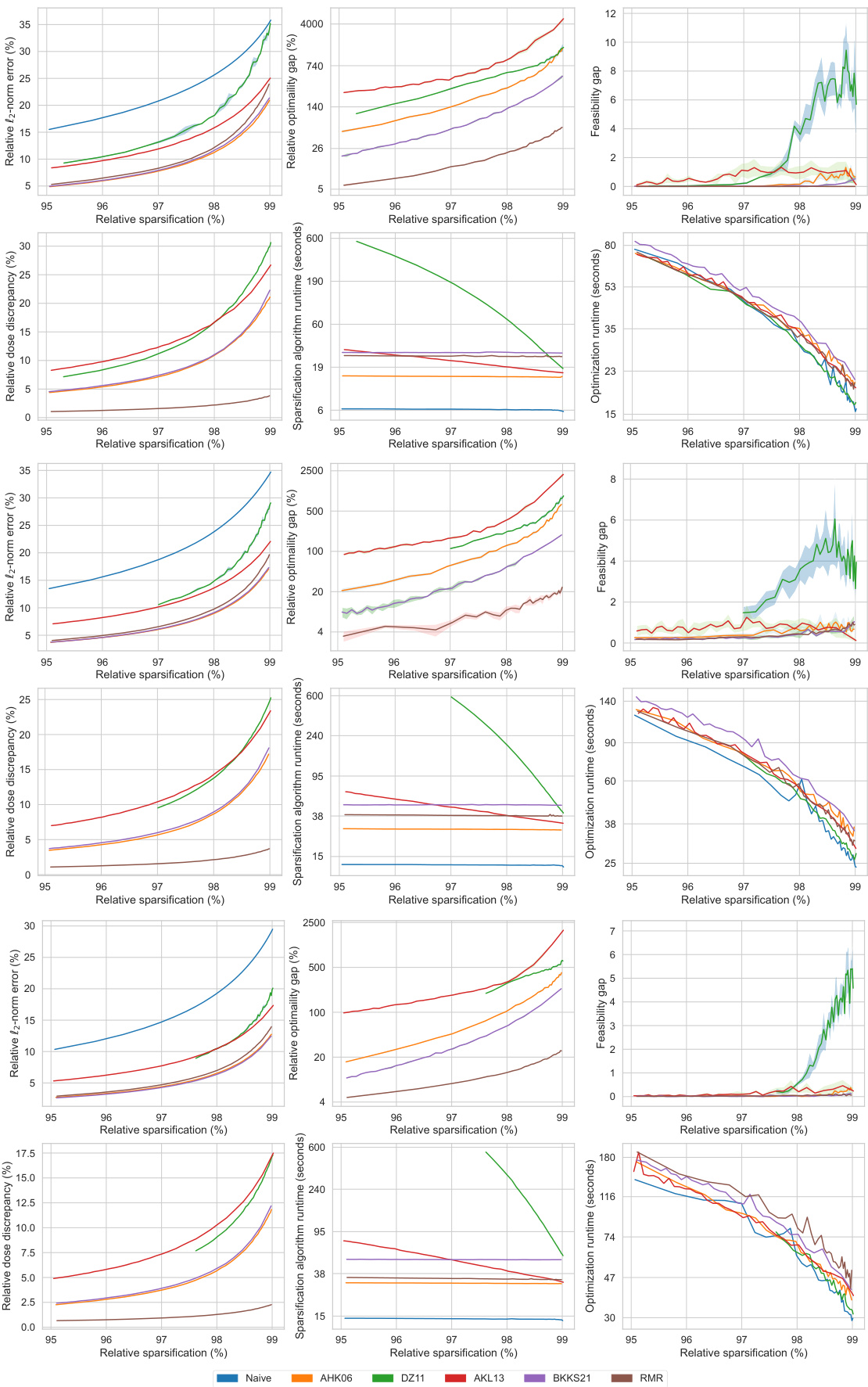
This figure displays the performance comparison of different matrix sparsification algorithms across various sparsity levels for a single lung cancer patient. The metrics shown are relative l2-norm error (measuring the accuracy of the sparse matrix approximation), relative optimality gap (showing how close the solution of the approximate problem is to the optimal solution), feasibility gap (how much the constraints are violated), relative dose discrepancy (how much the delivered radiation dose differs from the calculated dose), algorithm runtime (the time needed to generate the sparse matrix), and optimization runtime (the time needed to solve the optimization problem using the sparse matrix). Each metric is plotted against the relative sparsification level, illustrating the trade-off between computational efficiency and accuracy of the different approaches.
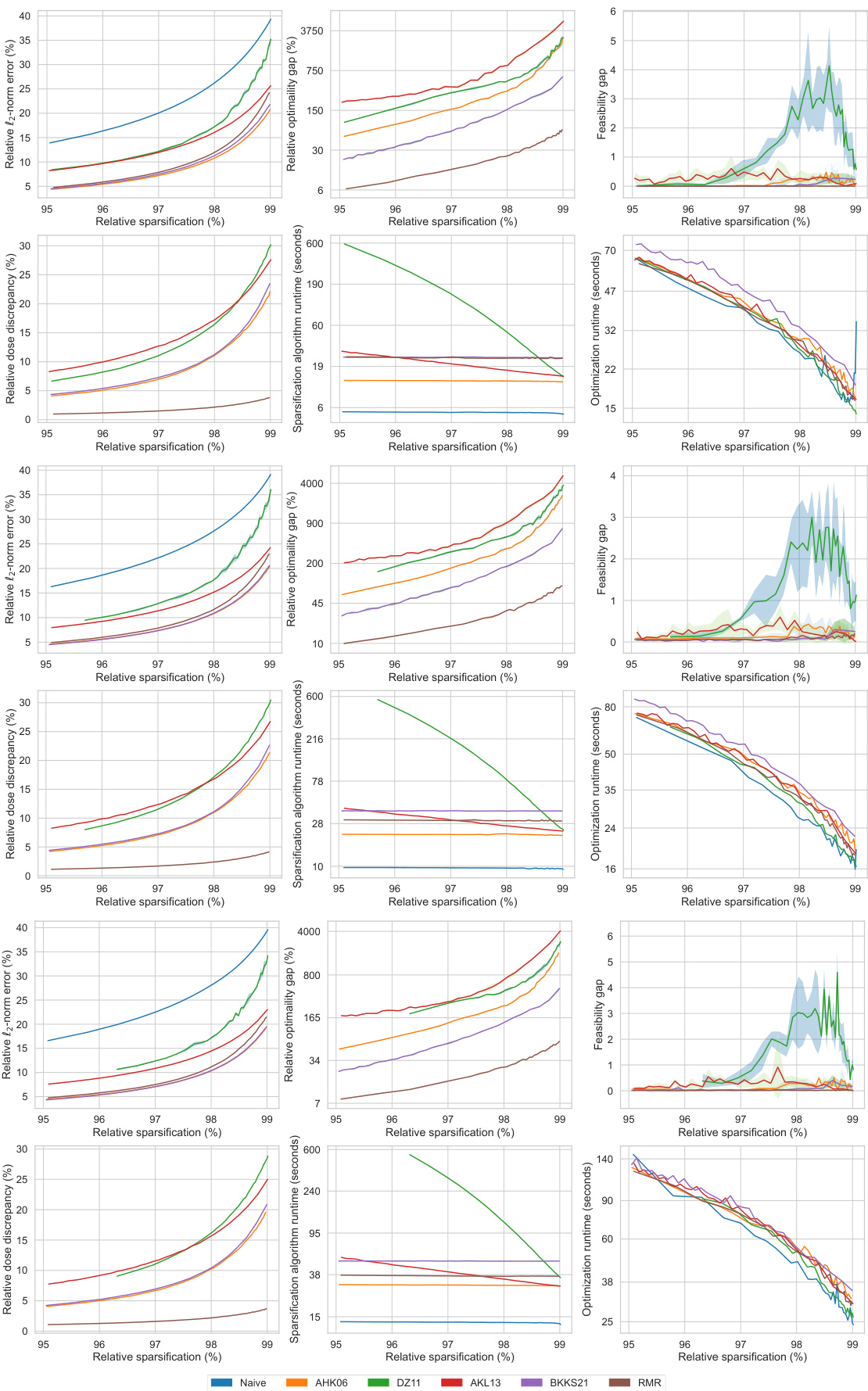
This figure presents a comprehensive comparison of different matrix sparsification algorithms (Naive, AHK06, DZ11, AKL13, BKKS21, and RMR) across various sparsity levels (95% to 99%). It evaluates each algorithm’s performance based on six key metrics: relative l2-norm error (measuring the accuracy of the sparse approximation), relative optimality gap (quantifying the sub-optimality introduced by the approximation), feasibility gap (assessing how much the constraints of the original problem are violated by the approximation), relative dose discrepancy (measuring the difference between actual and approximated doses received by the patient), algorithm runtime (the time taken for the sparsification process), and optimization runtime (the time taken to solve the optimization problem using the sparse matrix). The figure visually demonstrates how each metric changes as the sparsity level increases, allowing for a direct comparison of the algorithms’ trade-offs between accuracy and computational efficiency.
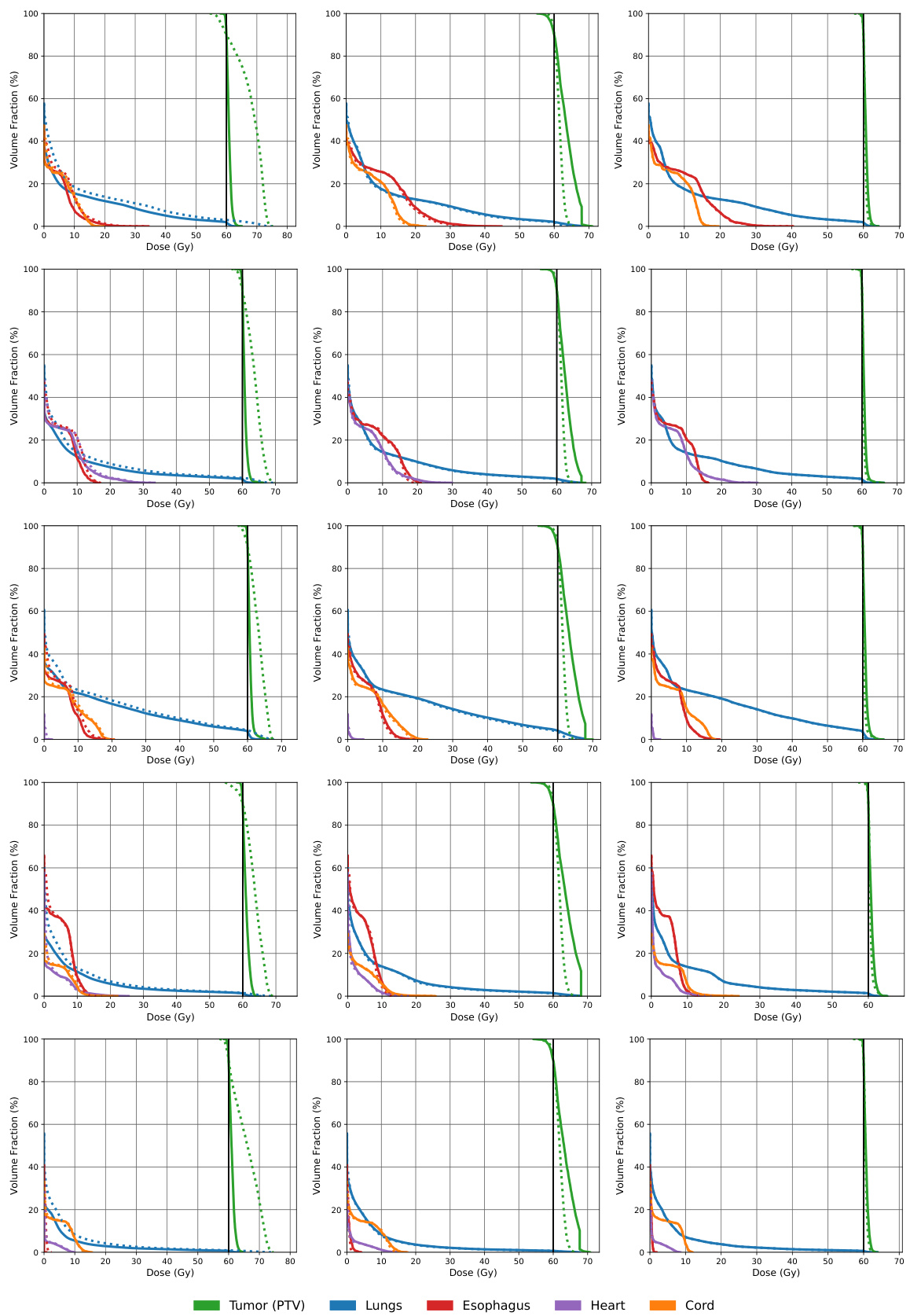
This figure compares the dose volume histograms (DVHs) for five lung cancer patients across three different methods: a naive approach, the AHK06 algorithm, and the proposed RMR algorithm. DVHs show the percentage of an organ’s volume that receives a certain dose of radiation. The closer the dashed line (approximated dose) is to the solid line (actual dose), the better the approximation. The figure shows that RMR offers the best approximation, often having the dashed and solid lines overlap, indicating high accuracy.
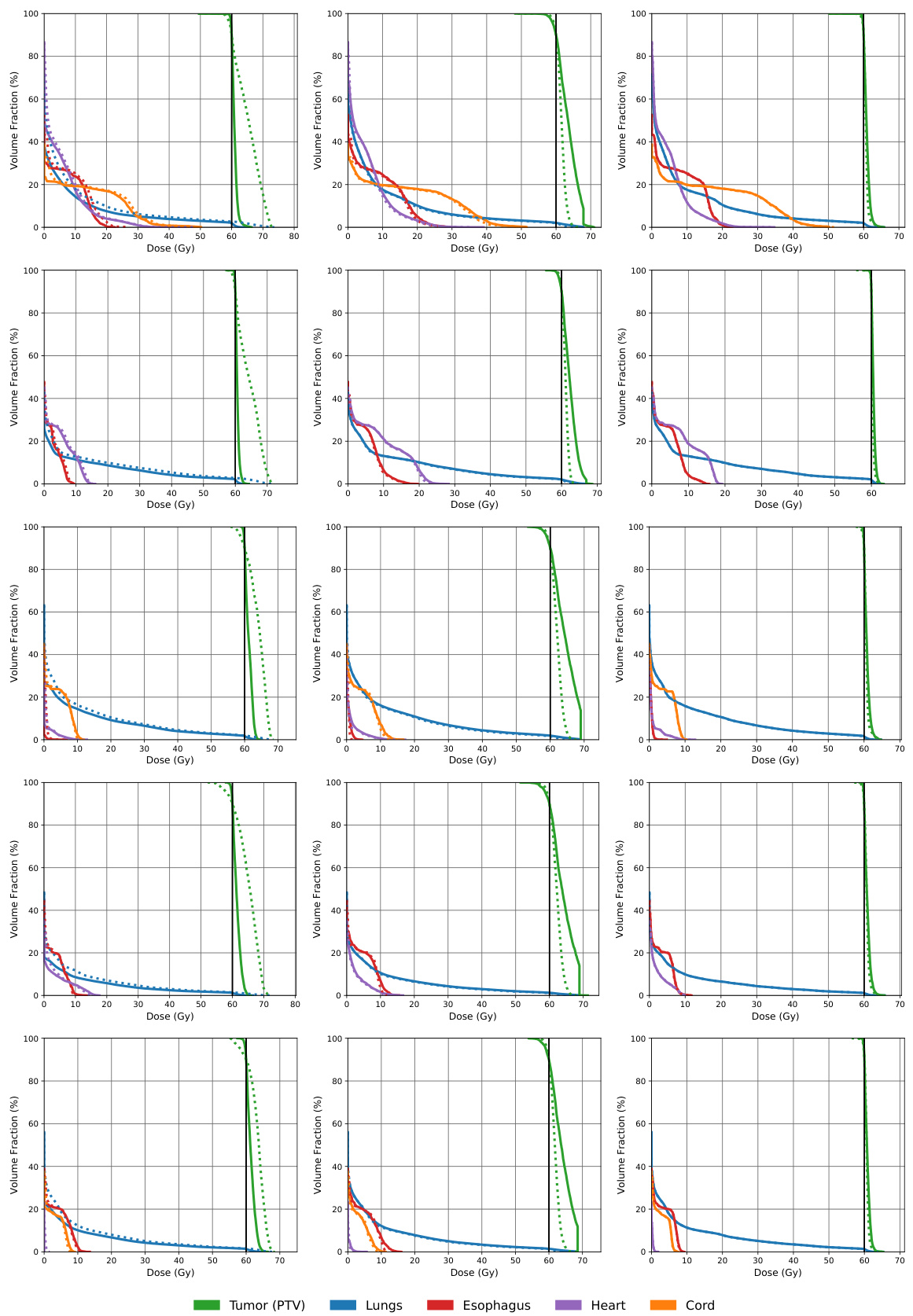
This figure compares the dose volume histograms (DVHs) for five lung cancer patients across three different matrix sparsification methods: the naive method, the AHK06 method, and the RMR method. DVHs show the percentage of an organ that receives at least a certain dose of radiation. The closer the dashed lines (approximated dose) are to the solid lines (actual dose), the better the approximation. The figure shows that the RMR method produces the most accurate dose approximation, as the dashed and solid lines almost completely overlap.

This figure displays the performance comparison of different matrix sparsification algorithms (Naive, AHK06, DZ11, AKL13, BKKS21, and RMR) across various sparsity levels. The metrics used for comparison include relative l2-norm error, relative optimality gap, feasibility gap, relative dose discrepancy, algorithm runtime, and optimization runtime. Each metric is plotted against the relative sparsification level, providing a comprehensive view of the trade-offs between accuracy and computational efficiency for each algorithm. The data is from a single lung cancer patient.
This figure compares the performance of different matrix sparsification algorithms (Naive, AHK06, DZ11, AKL13, BKKS21, and RMR) across various sparsity levels (95% to 99%). The metrics compared include relative l2-norm error (how well the sparse matrix approximates the original), relative optimality gap (difference in the optimal objective value between the original and the approximated problem), feasibility gap (constraint violation in the approximated problem), relative dose discrepancy (difference in doses between original and approximated problems), algorithm runtime (time for the sparsification algorithm), and optimization runtime (time to solve the optimization problem using the sparse matrix). This allows assessment of each algorithm’s trade-off between accuracy and computational efficiency.
This figure presents a qualitative comparison of radiation dose maps generated using three different approaches: the naive method, the RMR method, and dose labels. The dose maps visually represent radiation distribution with color-coding overlaid on a medical image. Ideally, high-dose regions (red) should match the tumor’s shape with minimal radiation spillover into healthy tissues. The figure shows that using the RMR sparse matrix, in contrast to the naive sparse matrix, results in less radiation exposure to healthy tissues.
More on tables
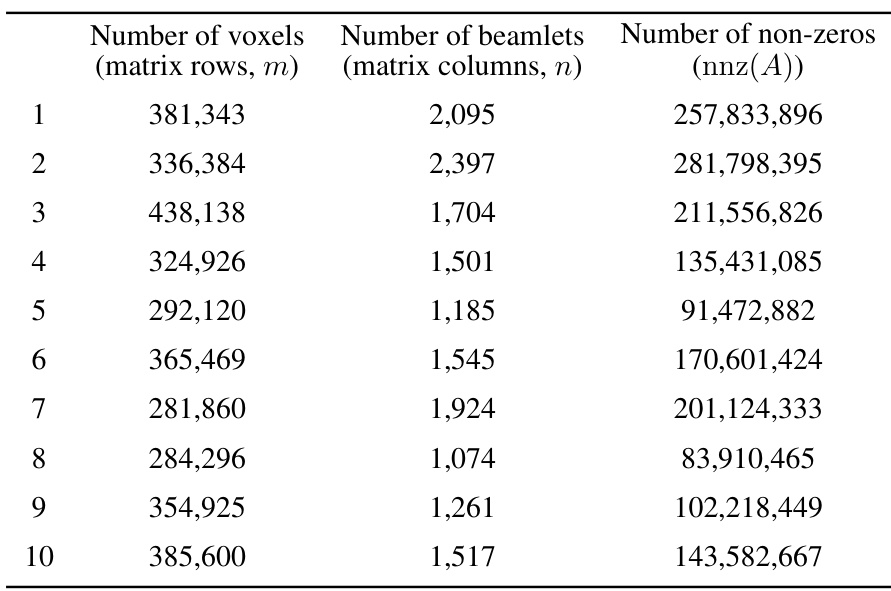
This table presents the characteristics of the datasets used in the study. For each of the ten lung cancer patients, it provides the number of voxels (matrix rows, m), the number of beamlets (matrix columns, n), and the number of non-zero elements (nnz(A)) in the dose influence matrix. These values reflect the scale and sparsity of the optimization problems solved in the study.
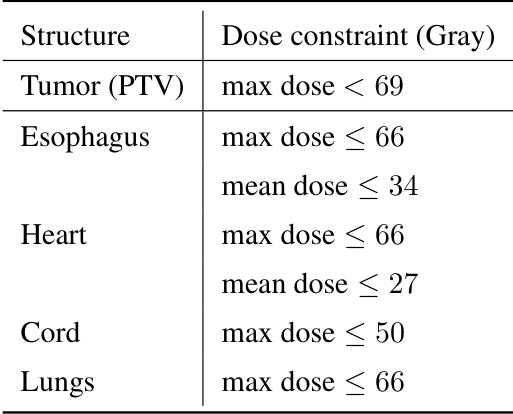
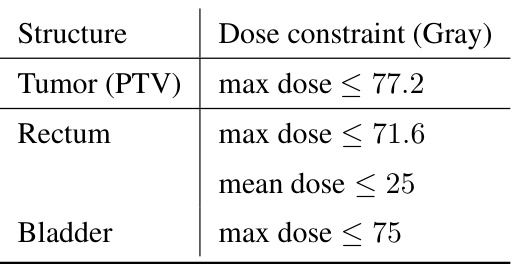
This table lists the recommended maximum and mean dose constraints in Gray for different organs during lung cancer radiotherapy treatment. These constraints are used to guide the optimization process and ensure that healthy tissues receive minimal radiation exposure while maximizing the dose delivered to the tumor.
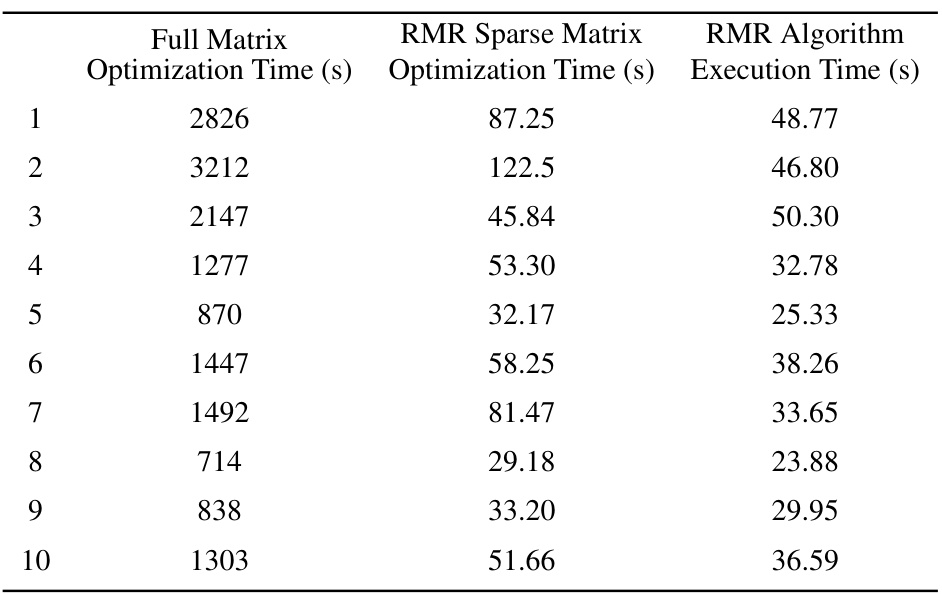
This table compares the optimization runtime for solving the constrained optimization problem using three different approaches: the full dose influence matrix, the RMR sparse matrix (with 98% sparsity), and the RMR algorithm itself. For each of ten patients, the table shows the time taken for optimization with the full matrix, the time taken for optimization with the RMR sparse matrix, and the execution time of the RMR algorithm used to create the sparse matrix. This allows for a comparison of the computational efficiency gains achieved by using the sparse matrix approximation.
This table presents the dimensions of the dose influence matrices for ten lung cancer patients. Each row represents a patient, and shows the number of voxels (rows in the matrix), the number of beamlets (columns in the matrix), and the total number of non-zero elements within the matrix. These values illustrate the scale of the optimization problems addressed in the paper, and the impact of matrix sparsification on computational cost.
This table compares different matrix sparsification algorithms (AHK06, DZ11, AKL13, BKKS21, and RMR) in terms of their theoretical guarantees. Specifically, it contrasts the number of non-zero elements in the resulting sparse matrix and their failure probability, both of which are functions of the error rate (τ). The table highlights the different scaling behavior of the algorithms with respect to error rate (some are inversely proportional to τ while others are inversely proportional to τ²) and provides insights into the trade-offs between sparsity and accuracy.
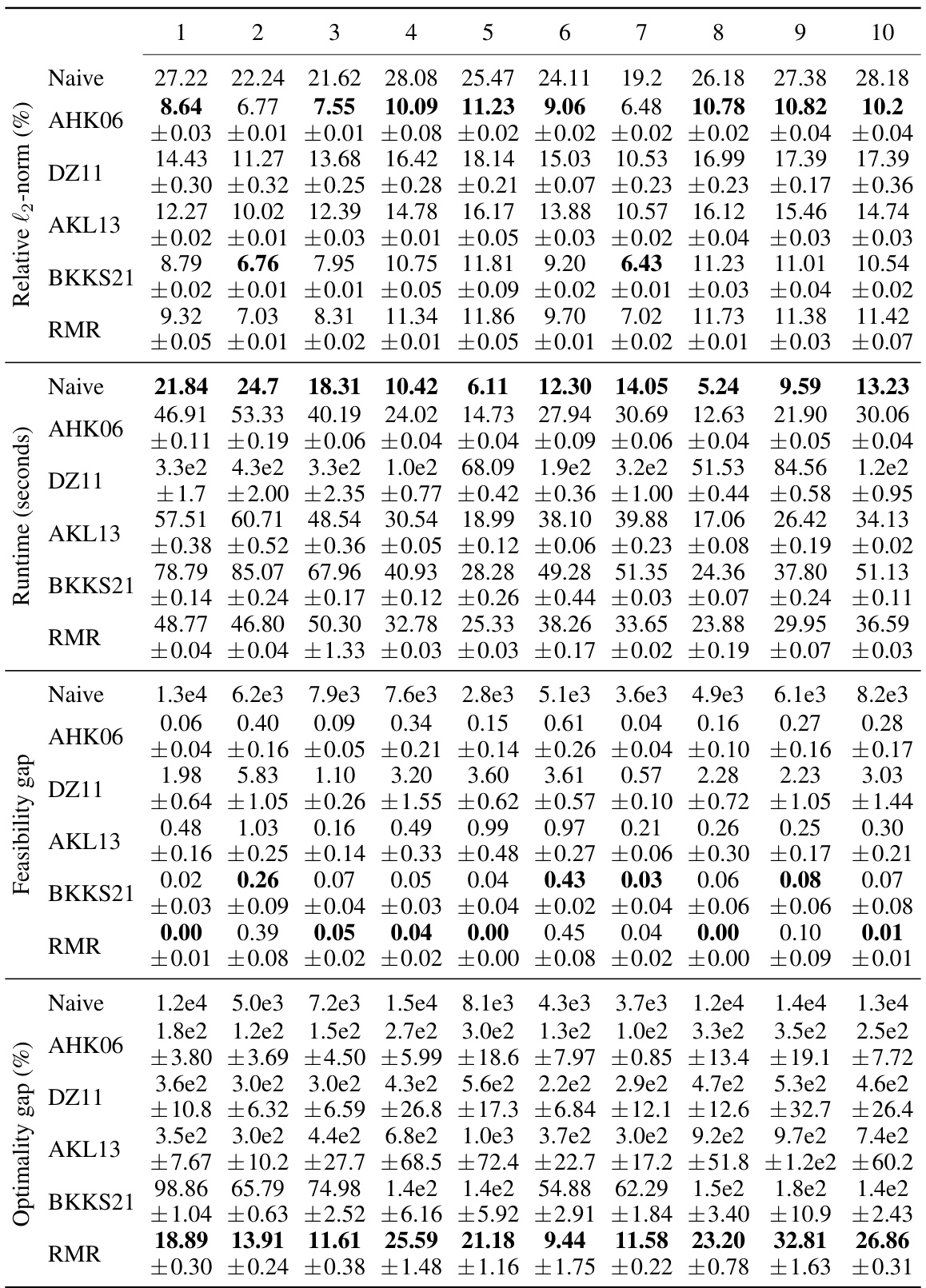
This table compares the performance of different matrix sparsification algorithms across ten lung cancer patients, with a fixed sparsity level of 98%. The metrics evaluated include relative l2-norm error (measuring the accuracy of the approximation), algorithm runtime (measuring the speed of the algorithm), feasibility gap (measuring how much the constraints of the original optimization problem are violated by the solution of the approximated problem), and relative optimality gap (measuring how sub-optimal the solution is to the original optimization problem). The results highlight the trade-offs between computational efficiency, accuracy, and constraint satisfaction.
Full paper#