A Universal Growth Rate for Learning with Smooth Surrogate Losses

↗ arXiv ↗ Hugging Face ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it establishes a universal square-root growth rate for smooth surrogate losses, a prevalent choice in neural network training, impacting model selection and performance. It also introduces minimizability gaps as a key factor in comparing loss functions, opening avenues for improved learning bounds and algorithm design.

Visual Insights

#

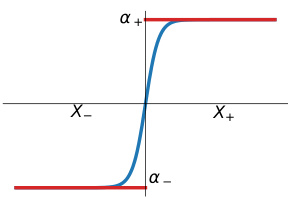
🔼 The figure shows a sigmoid activation function used to approximate a piecewise constant function. The horizontal axis represents the predictor values and the vertical axis represents the loss value. The sigmoid function smoothly transitions between two horizontal lines representing the minimum loss for each class (α− and α+). This illustrates how a sigmoid can approximate a best-in-class classifier composed of different constant values for each class, which is relevant for the discussion of minimizability gaps in the paper.

read the caption

Figure 1: Approximation provided by sigmoid activation function.

🔼 The table presents examples of H-consistency bounds for four common binary margin-based surrogate loss functions. Each row shows a different surrogate loss function (e.g., exponential loss, logistic loss, squared hinge loss, hinge loss), along with the corresponding H-consistency bound. These bounds relate the estimation error of the zero-one loss to the estimation error of the surrogate loss, including minimizability gaps (Me). The H-consistency bound shows how quickly the zero-one loss estimation error decreases as the surrogate loss estimation error is minimized.

read the caption

Table 1: Examples of H-consistency bounds for binary margin-based losses.

In-depth insights

#

Universal Growth Rate

#

The concept of a “Universal Growth Rate” in the context of machine learning loss functions is a significant contribution. It suggests that for a wide class of smooth surrogate losses (margin-based, comp-sum, and constrained losses), the rate at which the H-consistency bounds (measuring the convergence to the optimal zero-one loss) improve near zero error is universally a square root. This unifying result simplifies the analysis, enabling direct comparison across many different losses. The dependence on minimizability gaps highlights the importance of hypothesis set selection in learning bounds. Minimizability gaps, a key factor in H-consistency bounds, represent the difference between the optimal loss achievable within a restricted hypothesis set and the expected minimum loss for all possible functions. Analyzing these gaps provides valuable guidance for selecting the best surrogate loss for specific applications, ultimately improving generalization performance.

H-Consistency Bounds

#

The concept of H-consistency bounds offers a significant advancement in evaluating the performance of surrogate loss functions used in machine learning. Unlike traditional Bayes-consistency, which provides only asymptotic guarantees, H-consistency bounds offer non-asymptotic, hypothesis-set specific guarantees, making them significantly more informative in practical learning scenarios. These bounds establish a relationship between the estimation error of a target loss function (like the 0-1 loss in classification) and the estimation error of a surrogate loss function. The key innovation lies in incorporating minimizability gaps, which quantify the difference between the best achievable loss within a given hypothesis set and the expected infimum of the pointwise losses. This accounts for the limitations imposed by the choice of hypothesis set, offering a more realistic evaluation. The square-root growth rate near zero for smooth surrogate losses, demonstrated in the paper, is a key result. This rate is universal for many smooth losses, emphasizing the critical role of minimizability gaps in distinguishing between different surrogate loss functions. The detailed analysis of minimizability gaps provides crucial guidance for loss selection in practical applications.

Minimizability Gaps

#

The concept of “Minimizability Gaps” offers crucial insights into the discrepancy between the theoretically optimal performance achievable with a given loss function and the actual performance obtained when employing a restricted hypothesis set in machine learning. Minimizability gaps quantify the difference between the best possible expected loss within a hypothesis class and the expected infimum of pointwise expected losses. They highlight the limitations of existing consistency bounds which only focus on the asymptotic behavior without explicitly considering the impact of a hypothesis set’s expressiveness. The analysis reveals that ignoring minimizability gaps leads to looser bounds, particularly in settings with limited hypothesis capacity. Therefore, incorporating the minimizability gap into the analysis of surrogate losses offers more favorable and realistic guarantees. Smooth loss functions, although exhibiting a universal square-root growth rate near zero, demonstrate that minimizability gaps play a key role in guiding surrogate loss selection and interpreting the effectiveness of different learning algorithms. Hence, future research should focus on improving the practical applicability of H-consistency bounds by further investigating techniques to effectively estimate or bound these critical gaps.

Multi-class Analysis

#

A hypothetical “Multi-class Analysis” section in a machine learning research paper would likely delve into extending binary classification methods to handle multiple classes. This would involve discussing various loss functions suitable for multi-class problems, such as cross-entropy or hinge loss variants, and their properties. A key focus would be the generalization performance of different multi-class approaches, potentially comparing them empirically or through theoretical analysis. The analysis would likely address the challenge of handling class imbalance and techniques used to mitigate issues arising from disproportionate class representation. Furthermore, a discussion of algorithmic considerations, such as the choice of optimization method (e.g., SGD, Adam) and its impact on multi-class learning would be crucial. Finally, the section might also explore connections to other multi-class problems like multi-label classification or structured prediction highlighting the unique challenges and methodologies involved.

Future Directions

#

The research paper’s “Future Directions” section would ideally explore extending the universal square-root growth rate findings to a broader class of surrogate loss functions. Investigating the impact of different data distributions on this growth rate is crucial, potentially revealing scenarios where tighter bounds are achievable. Furthermore, a detailed exploration of how specific distributional assumptions could refine the results would provide valuable insights. This could include analyzing heavy-tailed distributions or scenarios with class imbalances. Another important avenue would be to investigate the interaction between minimizability gaps and Rademacher complexity bounds more deeply to derive tighter learning bounds and enhance the practical utility of H-consistency analysis. Finally, developing novel surrogate loss functions that minimize minimizability gaps in various settings, especially for multi-class problems with high dimensionality, could lead to significant advancements in the field. This section should also consider practical implications of applying these findings to different machine learning applications and architectures.

More visual insights

#

More on tables

🔼 This table presents examples of H-consistency bounds for several comp-sum loss functions. Each row shows a different comp-sum loss function (defined by its Φ(u) function) and the corresponding H-consistency bound in terms of the zero-one loss, the surrogate loss, and their respective minimizability gaps. The bounds highlight the square-root relationship between the surrogate estimation error and the zero-one estimation error, a key finding of the paper.

read the caption

Table 2: Examples of H-consistency bounds for comp-sum losses.

🔼 This table presents examples of H-consistency bounds for various constrained losses in multi-class classification. The table shows how the H-consistency bound varies depending on the choice of constrained loss function (e.g., exponential loss, squared hinge loss). Note that these bounds incorporate the minimizability gap, a key element differentiating them from excess error bounds.

read the caption

Table 3: Examples of H-consistency bounds for constrained losses with ∑y∈Y h(x, y) = 0.

Full paper

#